基于車輛成組的V2V協同計算卸載策略研究

0 引言

隨著無線通信技術和車載互聯網的爆炸性發展，越來越多的車輛配備了具有通信、存儲、計算和人機交互能力的車載單元［1］。許多智能交通應用程序可以在車載單元上運行，同時也有相當比例的車載應用對計算資源與能源需求極大，被稱為計算密集型應用。面對這些應用，單個車載單元的計算能力可能無法完全滿足要求。車聯網邊緣計算（VEC）的出現為解決這一問題提供了新的途徑［2］。VEC 與移動邊緣計算（MEC）相比，其終端從個人移動設備變為了高速移動的車輛。通過將核心網的計算資源部署到車輛網絡的邊緣，路側單元（RSU）覆蓋范圍內的車輛可以將部分或全部任務卸載給部署在RSU 的MEC 服務器以獲得更好的計算服務，這種方式稱為車輛到基礎設施（V2I）卸載［3］。另一種方法是將任務卸載給其他有計算能力的車輛，稱為車輛到車輛（V2V）卸載［4］。與V2I卸載相比，V2V 卸載可以充分利用其他車輛的計算資源，緩解路邊MEC服務器的壓力。

通過V2I 卸載，車輛可以將計算任務卸載到部署在RSU的MEC服務器來完成計算。然而，在典型的車載網絡場景中，車輛在計算卸載過程中高速移動，使得V2I 卸載面臨許多問題，如車輛可能在計算結果返回之前離開RSU 覆蓋的小區，高速移動會影響無線鏈路質量。在熱點地區，由于交通擁擠和移動終端數量過多，RSU 會承受很大的負載［5］。因此，如何充分利用閑置車輛的大量計算資源來降低RSU 的負載是計算卸載的關鍵問題之一［6］。文獻［7］考慮將卸載到負載過重RSU 的計算任務轉移到周圍負載較輕的RSU，并通過車輛將計算結果帶回輕負載RSU 的范圍內。在文獻［8］中，V2I卸載問題被視為車輛與RSU 之間的匹配問題，通過求解任務車輛與RSU 之間的最優匹配來最小化所有車輛的平均計算時延。在文獻［9］中，計算任務被分成若干個無依賴關系的子任務，分別卸載到沿途經過的各個RSU，通過車速、鏈路質量、RSU 覆蓋半徑、子任務大小等因素預測經過每個RSU 覆蓋小區的時間，以此來分配子任務數量，確保計算結果的返回。

對于車載網絡中的V2V 卸載，車輛通常成組來共享信息并互相幫助完成計算任務。文獻［10］提出了一種協同車輛邊緣計算網絡架構，該網絡中的多個相鄰車輛組成一個組，組中的車輛可以通過無線鏈路相互通信和協作完成計算任務。文獻［11］考慮了車組內成員的協作以及計算任務的可分割性，其中組內的不同車輛具有不同類型的計算任務。文獻［12］將計算任務分為順序子任務和依賴子任務，并提出了一種任務調度算法確定任務的最優計算順序。在文獻［13］中，作者將計算任務劃分為若干有先后順序的子任務，并將任務分配問題看作并行處理器的最小完成時間問題，提出了一種基于列表調度的任務分配算法，以最小化任務的總完成時延。

然而，上述研究并沒有充分考慮計算卸載過程中車組內的車輛之間保持穩定連接的時間以及車輛在計算過程中離開車組的情況。本文聯合考慮車組成員能保持穩定連接的時間和車輛突發離組的情況，具體分析了車輛因故障離組和中途主動離組的2 種情形。對計算任務根據不同類型劃分子任務，設計了一個動態的組內計算任務分配算法，其中計算任務卸載總時延包括任務上傳時延、任務計算時延和結果返回時延。為了使整個車組計算任務的總時延最小，提出了一種車組內計算任務分配算法。該算法調整了子任務的分配方式，通過迭代實現總時延最小。

1 系統模型

1.1 網絡拓撲

本文研究單向直行道路上，車組在行駛過程中的計算卸載問題，場景如圖1所示。在該場景中，路側單元RSU 均勻分布在道路兩側，其覆蓋范圍互不重疊。這n個RSU 記作R={R1,R2...Ri...Rn}，其中Ri表示第i個RSU。每個RSU 的覆蓋半徑為r，相鄰RSU 之間由光纖連接。同車道內前后M輛車組成一個車組。用U=(U0,U1...Ui...UM-1)表示車組內的車輛，其中U0的計算任務僅靠自己不能完成，稱為任務車；組內其他車輛或多或少有可以提供給任務車的空閑計算資源，稱為服務車。本章中任務車U0的計算任務分為4 種類型，分別是圖像處理、視頻處理、交互式游戲、增強現實［14-16］，可以用L=(LA,LB,LC,LD)表示，每種類型的任務可以劃分成若干相等大小的不相關的子任務，以I作為子任務劃分的大小單元。

整個車組以共同的速度v向前行進，車組內每一輛車的計算能力分別為f=(f0,f1,...,fm-1)，單位是CPU圈數/s，其中f0是本地計算的計算能力。

1.2 通信模型

在車輛形成車組后，由任務車U0作為車頭來協調組內車輛和分配計算任務。組內車輛分享行駛路線使得U0可以獲取組內各車輛能與車組保持穩定卸載的時間信息，用τ={τ1,τ2...τm-1}分別表示組內車輛預計離開車組的時間節點。要盡量保證分配給車輛Ui的計算任務在τi時間內完成并返回。組內車輛通過LTE-V 方式進行通信，根據香農公式可知任務上傳到組內服務車的速率如式（1）所示。

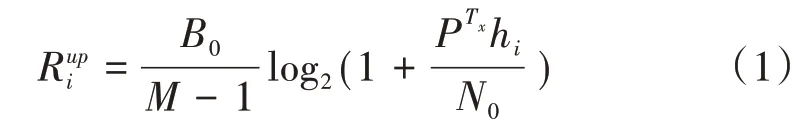
式中：

B0——分配給任務車的信道帶寬

h——上行信道衰落系數

N0——高斯白噪聲功率

pi——卸載到第i輛車的子任務數量

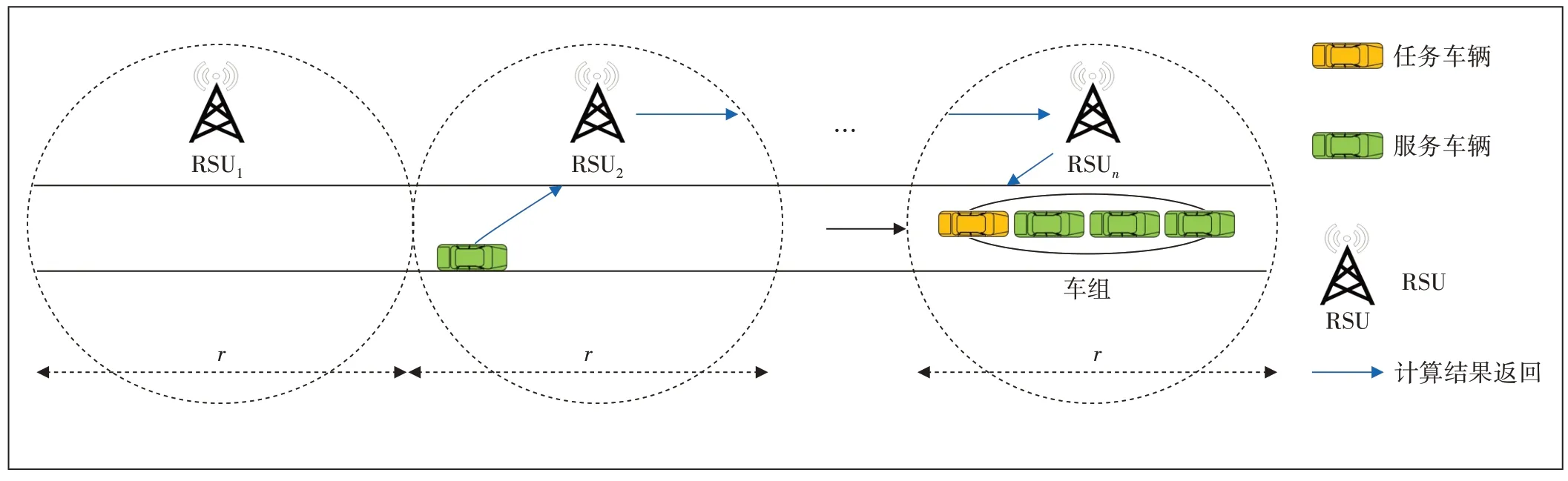
圖1 基于車輛成組的V2V卸載

任務車將帶寬分成M-1 份向組內每一輛服務車傳送分配的任務。卸載到第i輛車的任務傳輸時間如式（2）所示。

然后考慮計算結果的返回。由于返回的計算結果數據量通常很小，所以車組內的計算結果返回時延可以忽略不計。相鄰RSU 之間的光纖帶寬為B，子任務返回結果的數據量為dbit。任務返回時由于返回數據量很小，在RSU 之間的傳輸時間可以忽略不計，所以任務的返回時間主要由每次經過RSU的等待時間tw決定。子任務結果在RSU 之間返回時每經過一個RSU 都要有一個等待時延，經過n個RSU 則返回時延為ntw。

1.3 計算模型

本文假設車組內任務車輛的計算負載較重，且計算任務可以分割為若干相等大小的無依賴關系的子任務。執行計算任務需要耗費車輛的計算資源，通常使用執行該計算任務所要耗費的CPU 圈數來表示。任務執行時的復雜度用執行單位大小的任務需要耗費的CPU圈數來表示。假設4種不同類型任務的計算復雜度不同，分別是αA,αB,αC,αD，單位為CPU 圈數/bit。

考慮到任務分割，這4 類任務劃分為若干個子任務。4 種任務的每個子任務數量表示為NA,NB,NC,ND，子任務總數為N。

假設每個子任務的大小為Ibit。車組中的每輛車都由任務車輛分配了一定數量的子任務，分配給第i輛車的4 種任務的子任務數分別為pi={piA,piB,piC,piD}，則第i輛車的計算時延包括了4 種任務的計算時延，可通過式（3）計算。

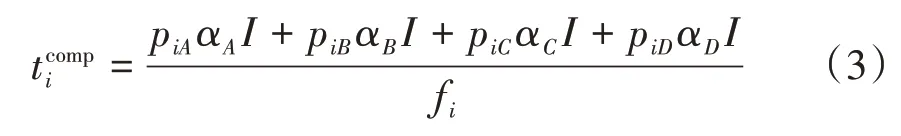
如上所述，組內的每輛車都被分配了這4 類任務中若干數量的子任務。本文通過調整每輛車被分配的子任務數量以降低總任務時延。

2 算法設計與實現

2.1 問題建立

對于組內被分配了計算任務的服務車輛，在任務計算完成后將計算結果直接返回給任務車輛。對于中途離開的服務車輛，考慮該車輛在離開車組后繼續進行計算工作，在計算完成后借助RSU 將計算任務返回給原車組中的任務車輛。

車輛離開車組的原因包括客觀因素與主觀因素。例如車輛在行駛過程中突發故障就屬于客觀因素。對于這種情況，可以根據已行駛時間估計車輛在未來一段時間內出故障的概率。對于第i輛車在任務過程中發生故障的概率可以用式（4）表示。

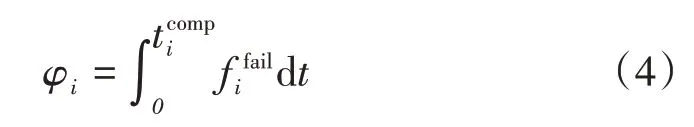
式中：

車輛也可能因駕駛者的主觀意愿臨時變更行駛方向或是需要在原地停留一段時間。對于這種情況，可以根據車輛歷史參與計算任務卸載的情況來推測本次任務過程中會發生主觀離組的可能性。假設車輛i歷史參與任務卸載的次數為yi，在任務過程中主動離開的次數為xi，通過車輛歷史參與任務卸載次數和中途離開的次數的比值可以推測其本次任務過程中離組的概率，具體如式（5）所示。

根據上面的2個因素，如果有一個因素發生，車輛就會離開車組。因此，第i輛車在任務過程中離開車組的概率可以用式（6）算出。

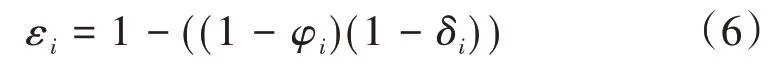
車組中所有車輛離開車組的概率，用ε ={ε1,ε2,...,εm-1}表示。假設車輛在離開車組后保持原地等待，同時不停止任務的計算過程，同時車組繼續保持前進。表示第i輛車離開車組的時刻。離開車組的車輛在完成計算任務后將計算結果返回給當前所在的RSU。車組在車輛i離開車組后經過的RSU 數量由式（7）給出。

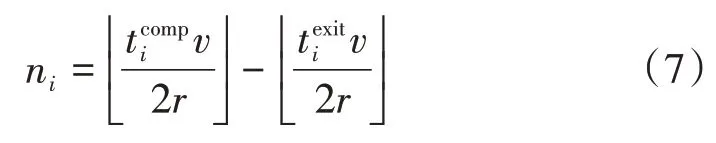
離開車組的服務車輛可以通過式（7）獲得車組當前所在的位置，并將結果返回到其范圍內的RSU。接下來，結果將在相鄰的RSU 之間傳輸，并最終到達車組當前所在的RSU。返回時延是由式（8）定義。

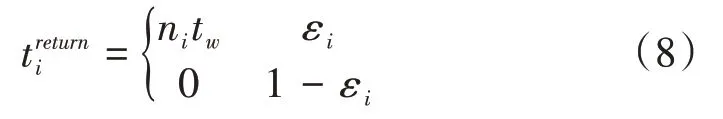
車組中每個車輛的總任務時延如式（9）所示，是任務上傳時延、任務計算時延和任務返回時延之和。

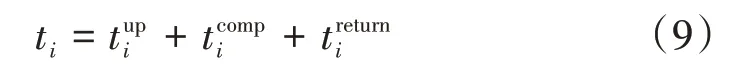
整個車組的總任務時延定義為車組中所有任務完成的時間，也就是組內最后一個車輛完成任務的時間。本文目標是通過優化組內車輛子任務的分配，以最小化任務完成的總時延。

因此，本文所討論的時延最小化問題可以表述為式（10）。

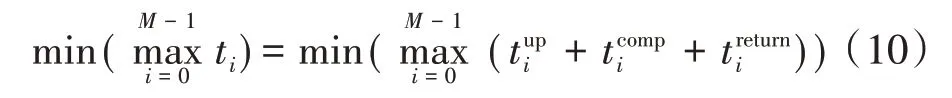
限制條件如下：

a）ti<τi

b）pi=piA+piB+piC+piD

d）0≤pi≤N

e）piA≤NA,piB≤NB,piC≤NC,piD≤ND

在上述條件中，條件a）是對每輛車中計算任務時延的限制，即每個車輛的計算任務必須在該任務的限制時延內完成。b）為子任務數量的約束條件，即分配給每個車輛的子任務數量等于4 種子任務數量的總和。c）以及d）是對每個車輛分配到子任務數量的限制，表明每輛車被分配到的每種類型的子任務數不超過車組內該種類子任務的總數。e）給出了車組內每種類型子任務數量上限的約束。

2.2 所提算法

通過分析發現，目標函數屬于混合整數規劃問題，存在最優解。這類問題在問題規模較小時可以通過暴力枚舉法在較短時間內找到最優解。然而當問題規模擴大后，暴力枚舉所需的時間則呈指數級增長。具體來看，式（10）相當于將N個任務放進M個容器內，一共有MN種可能性，時間復雜度為O(MN)，屬于NP-hard 問題。通過啟發式算法在較短的時間內找出一個次優解也是解決這類問題的一個途徑。本文使用模擬退火算法對該式進行求解，以得到較低時間代價的次優解。

在車組形成后，組內的服務車輛將路由、計算資源、歷史完成情況、故障概率等信息發送給任務車輛。任務車輛然后根據式（6）預測在計算任務過程中各個服務車輛的離開概率。首先任務車輛在分配每一個子任務前，通過式（2）、式（6）、式（8）、式（10）分別計算將此子任務卸載到每一個服務車輛的卸載時延，然后根據貪心算法依次將4種類型任務的子任務分給組內的服務車輛。貪心算法的策略是每個服務車輛被分配任務后累積自己的總任務時延，任務車輛將下一個子任務分配給當前總任務時延最小的服務車輛。在所有子任務分配完畢后，使用模擬退火算法優化子任務的分配方式，在所限定迭代次數內找出次優解。詳細算法步驟如圖2所示。

模擬退火算法的步驟包括以下幾步。

a）隨機在以下2個操作中二選一執行。

（a）隨機選擇車組內2輛車，交換其中一個不同類型的子任務。

（b）將車組內一輛車的一個子任務隨機分配給另一輛車。

b）計算新的總時延與之前總時延的差值。

c）如果差值為負，即通過任務交換或任務分配得到的時延比之前低，則接受此操作。否則則按一定概率接受此次操作，接受概率與當前溫度有關。

圖2 車組內協同計算任務分配算法

d）將當前溫度乘以冷卻系數得到新的溫度。

3 仿真與分析

本章通過仿真來驗證所提算法的性能。仿真場景如表1所示。車組內車輛的計算能力為f={3×107，5×107，2×107，3×107，3×107}圈/s，4種計算任務的計算復雜程度分別是30、15、40、20［17］。具體參數設置如表1 所示。

所選取的對比算法分別是隨機卸載算法以及貪婪卸載算法［18］。

a）隨機卸載算法：4 種計算任務將隨機數量的子任務分配給組內車輛。

b）貪婪卸載算法：貪婪分配算法在每次分配任務時都選擇能使當前總計算時延最小的車輛進行分配。

圖3 顯示當車組內子任務總數為80 時，通過3 種算法分配任務的車組最小時延與迭代次數的關系。車組速度設定為18 m/s。結果表明3 種算法都能在一定次數的迭代內達到收斂。其中貪婪分配算法能較快獲取極小值，在大約400 次迭代后將總時延降低到11.84 s。本文所提算法在約1 400 次迭代后收斂到最小值11.84 s。可以看出，當子任務總數量比較少時，這2種算法都能找到最小值。而隨機分配算法時延大于其他2種算法，性能較差。

表1 仿真參數設置

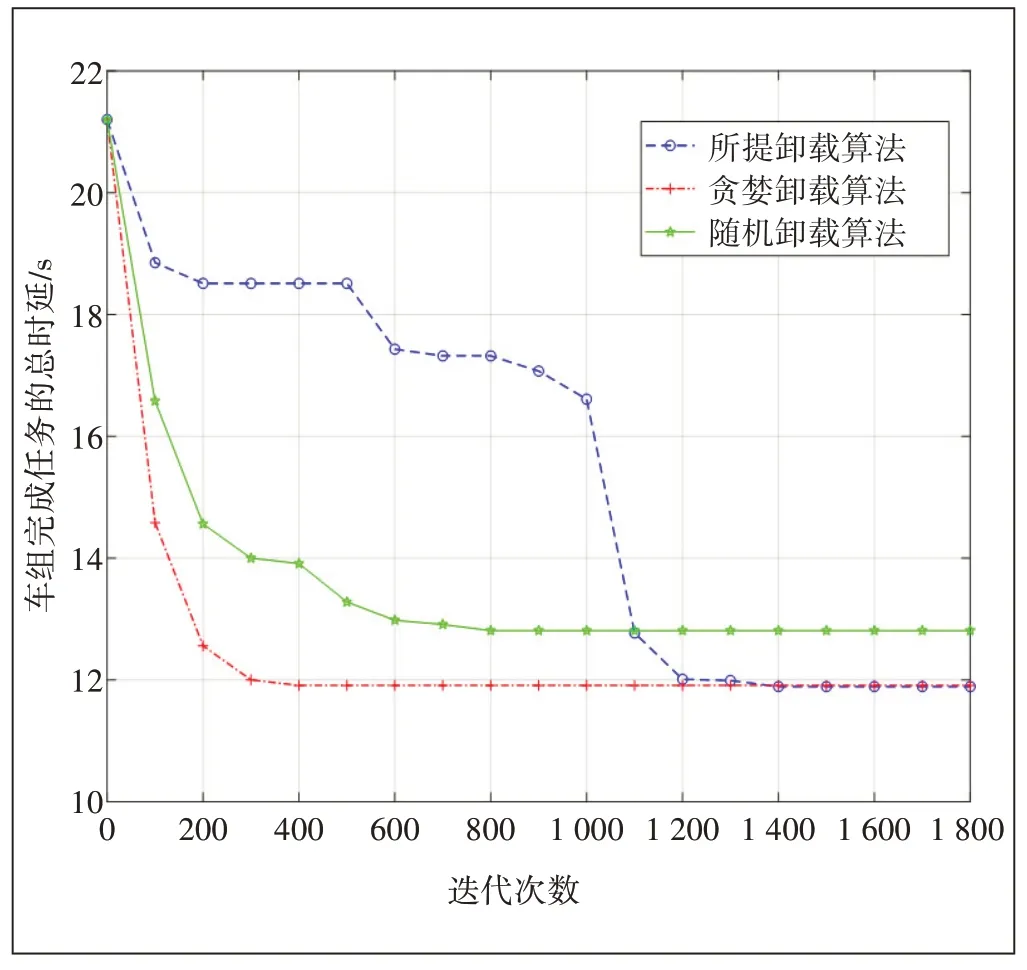
圖3 N=80時車組總時延隨迭代次數增加的變化

圖4 展示的是當組內子任務數增加到135 時，通過3種算法分配任務的車組最小時延與迭代次數的關系，其中車速仍固定在18 m/s。隨著任務數量的增加，可以看出，貪婪算法依舊可以較快地找到極小值，在約200次迭代后陷入局部極小值，由仿真結果來看，本文所提算法在約1 400 次迭代后找到了全局最小值17.64 s。隨機任務分配算法性能較差。

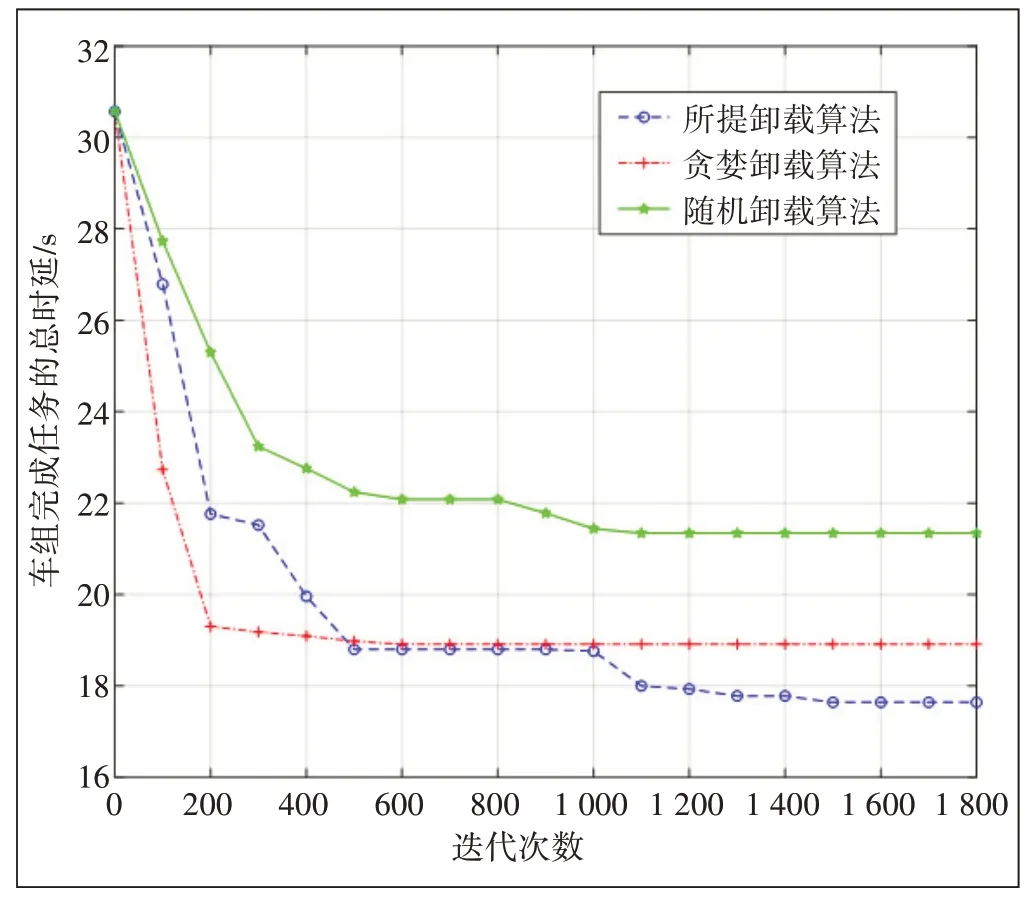
圖4 N=135時車組總時延隨迭代次數增加的變化

圖5表示車組的總任務時延隨車組內子任務數量增加而變化的情況。固定車組行駛速度18 m/s，可以看出，3 種任務分配算法得到的車組總時延均會隨車組內子任務數量的增長而增長。隨著子任務數量增加，在子任務數量超過100以后，貪婪算法的增長速率要明顯高于本文所提算法，這是因為子任務數量越多，貪婪算法越容易陷入局部最小，從而導致車組總任務時延較大。

圖6顯示了計算資源的利用率與組內車輛數量的關系。將計算資源的利用率定義為參與計算的車輛的平均計算時延與任務總完成時延之比［19］。計算資源利用率越高也即意味著每一個參與計算的車輛節點的計算時間越接近。從圖6 可以看出，當車組中車輛數增加時，車組的計算資源利用率隨之增加，這是因為，當參與任務的車輛越多，任務就可以在更短的時間內完成，所以離開車組的車輛返回結果所需的時間就越短，對整個車組的影響就更小。從圖6 的結果可以看出本文所提算法與其他2種算法相比能更合理地分配任務，提高計算資源的利用率。

圖7表示車組總任務完成時延隨車速增加而變化的情況。從圖7可以看出車組的總任務完成時延隨著車組速度的增加而增加。因為車組行駛速度越快，車組在任務進行過程中通過的RSU 單元越多，離開車輛組的車輛返回的任務結果所經過的RSU 就越多，任務結果返回到車輛組的時間也就越長。

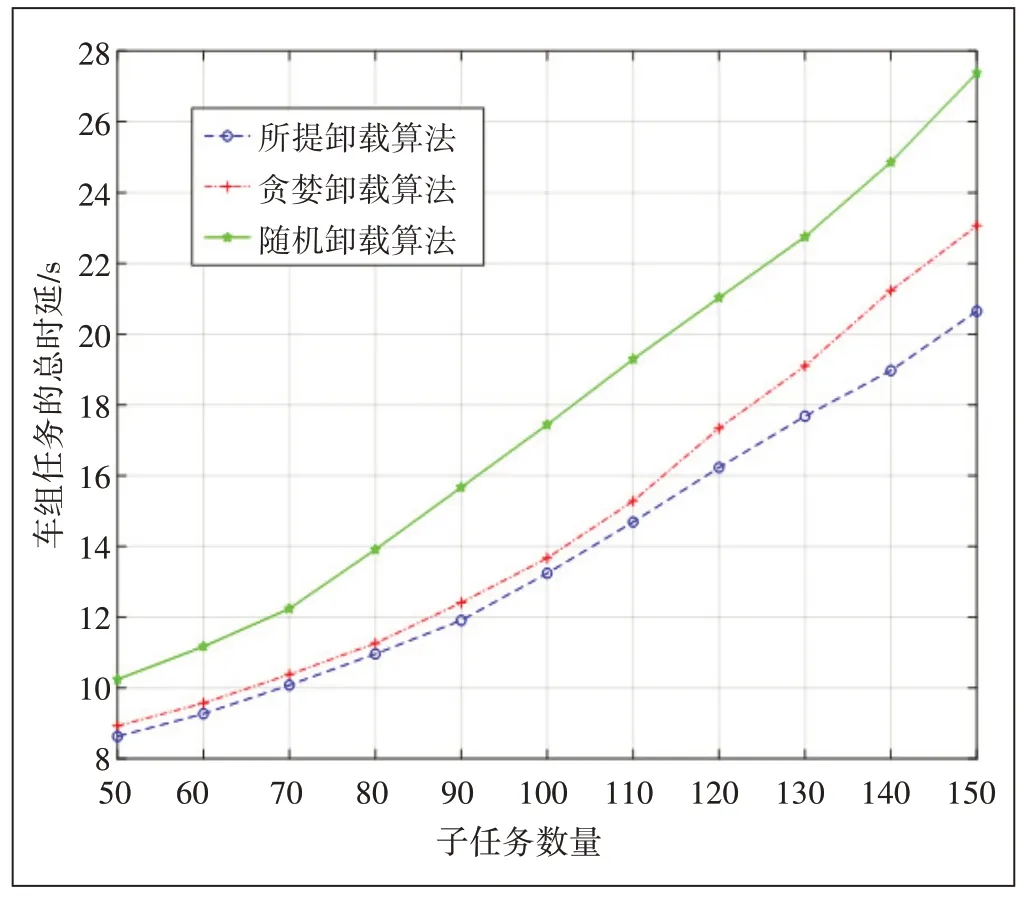
圖5 車組平均任務時延隨子任務數量的變化

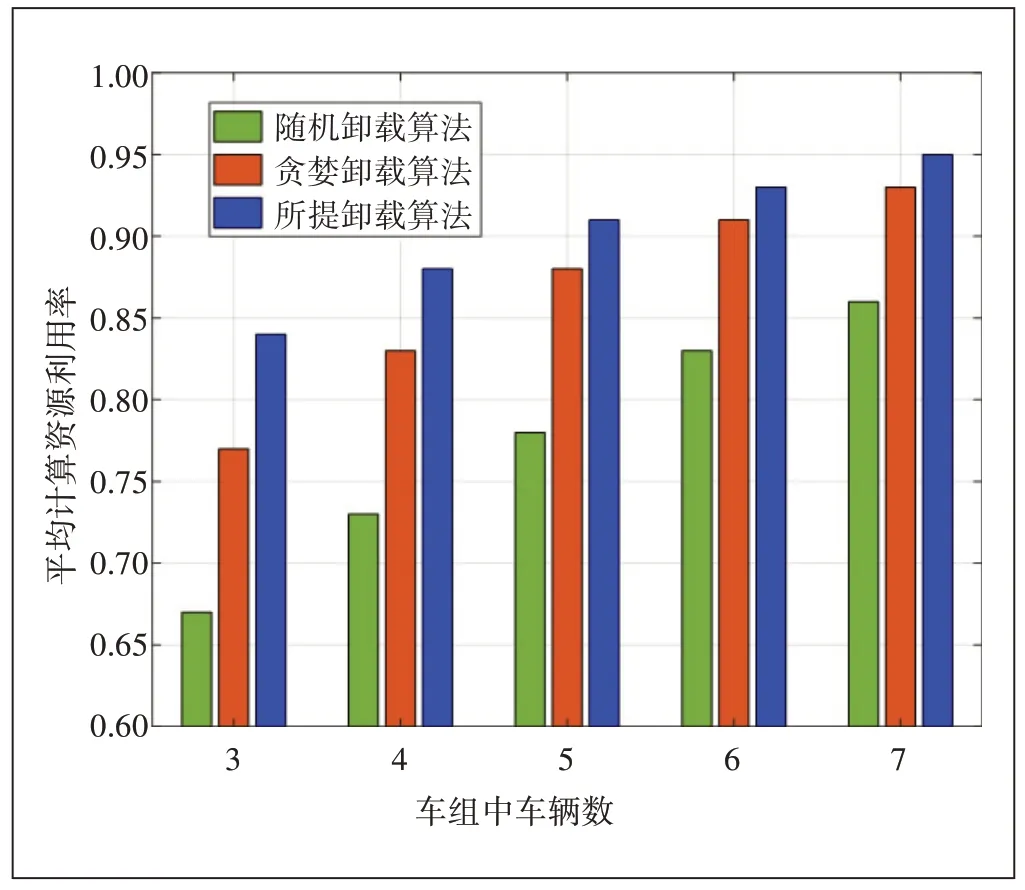
圖6 車組平均計算資源利用率隨車輛數增加的變化

4 結束語

本文對基于車輛成組的組內V2V 計算任務卸載問題進行了研究，提出了一種考慮車輛在計算卸載過程中離開車組的任務分配算法。首先介紹了研究背景與網絡模型。然后聯合考慮車組成員能保持穩定連接的時間和車輛因故障突發離組的情況，具體分析了車輛離組的2種情形并建模。將計算任務劃分成不同類型的子任務，并設計了一個動態的組內計算任務分配算法。該算法調整了子任務的分配方式，通過迭代實現總時延最小。最后，通過仿真對所提算法的有效性進行了驗證。

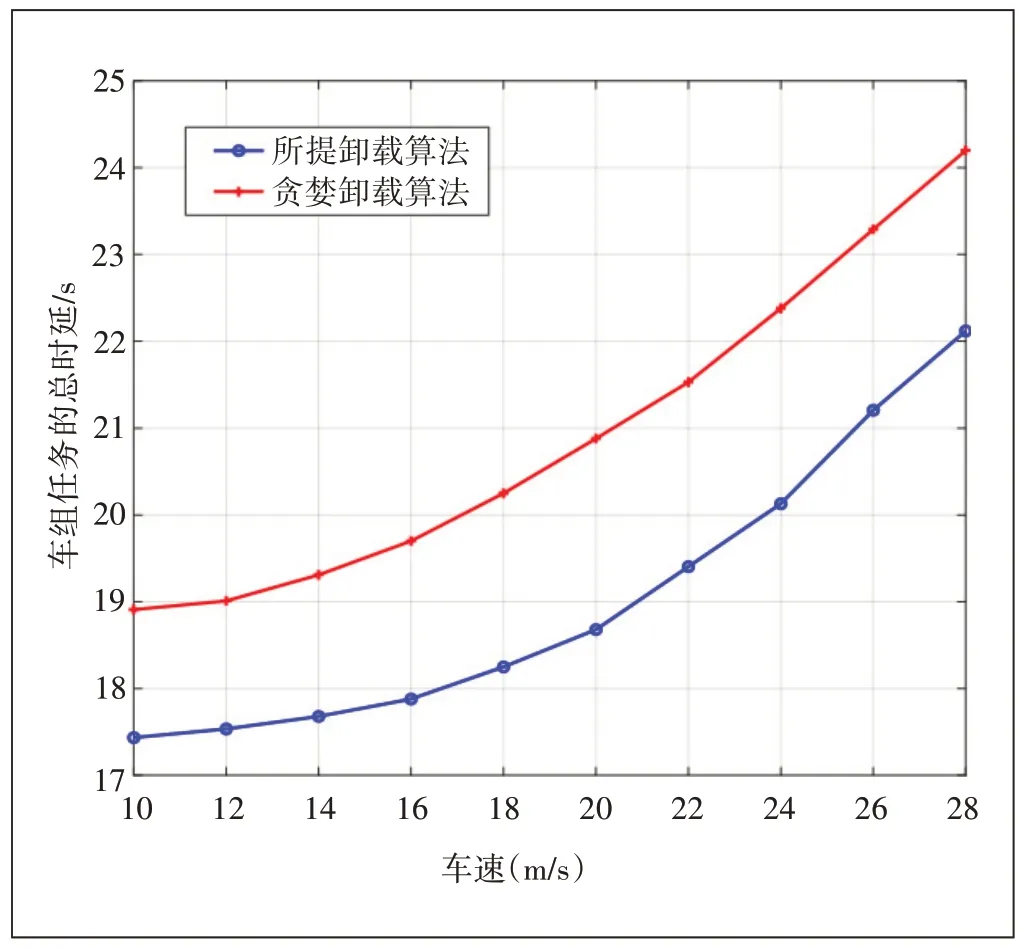
圖7 車組總時延隨車速的變化