基于灰色聚類的航空裝備可靠性評估模型?

（海軍航空大學青島校區(qū) 青島 266000）

1 引言

可靠性分析與評估是生產(chǎn)管理中的重要一環(huán)，通過評估與分析，能夠盡快發(fā)現(xiàn)生產(chǎn)活動中的一些不合理之處，并及時做出調(diào)整。對于軍隊來說，可靠性分析與評估對于裝備能否發(fā)揮其應有效能，反饋日常維修保障效果的意義也十分重大。實際上，針對可靠性評估的研究從未停止過，常用的可靠性建模方法有可靠性框圖法、故障樹分析法、馬爾可夫鏈、Petri網(wǎng)絡［1］、失效模式和后果分析等［2］。目前，國內(nèi)外學者在航空裝備可靠性相關問題上有了一系列的研究成果，尤其是在民航領域，已經(jīng)建立了相應的可靠性評估體系，如使用Kaplan-Meier估計來求解飛機部件的可靠性［3］，使用貝葉斯分類器來建立通用航空機隊的可靠性模糊識別模型［4］。在軍用航空領域，同樣對該課題有著一定的研究，如針對航空武器試飛階段的可靠性評估［5］，驗證使用現(xiàn)場數(shù)據(jù)對航空裝備進行可靠性評估的效果等［6］。事實上，航空裝備可靠性狀態(tài)容易受到人員、飛機的型號、服役時間、自然環(huán)境和組織管理等諸多因素的影響，具有隨機性、波動性、模糊性和不確定性等特征，僅僅依靠統(tǒng)計方法是難以確定的，需要一種新的方法來客觀地評估可靠性。

2 航空裝備可靠性指標的確定

航空裝備的可靠性評估的前提是對可靠性指標進行選取，指標要盡可能反映部隊日常的維修管理狀態(tài)，同時選取的指標也必須要具備可獲取、可量化、可監(jiān)控等特性，也應當包含可以反映飛機固有特性、使用性、維修性等特性［7］。

軍用航空的規(guī)模一般較小，機型組成復雜性也較低（通常一個團只保有一種型號的飛機），在數(shù)據(jù)采集時也會有一定的限制，所以，在選取指標時需要綜合考慮上述因素。

通過咨詢專家，結(jié)合部隊實際情況與管理經(jīng)驗，最終選取的航空裝備可靠性指標：1）單個月單架次平均飛行時間：單個月每架次飛機執(zhí)行飛行任務的平均時間。2）單月平均故障間隔時間：指飛機兩次故障之間平均經(jīng)過的故障時間。3）預防性維修效率：預防性維修發(fā)現(xiàn)的故障數(shù)量占全部故障數(shù)量的比例。4）飛機任務架次比例：單月任務架次占全部架次的比例。

3 灰色變權聚類

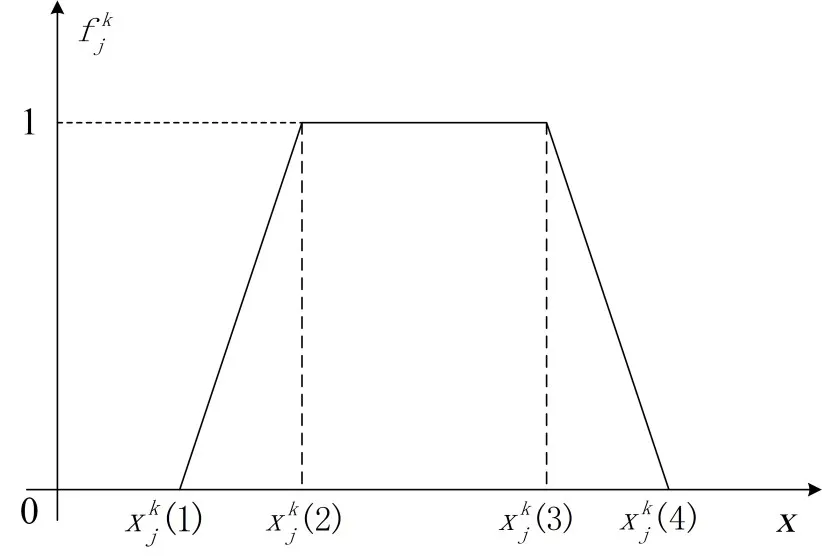
圖1 典型白化權函數(shù)圖像

當白化權函數(shù)出現(xiàn)一些如圖2中的特殊情況時，其表示方法略有不同。

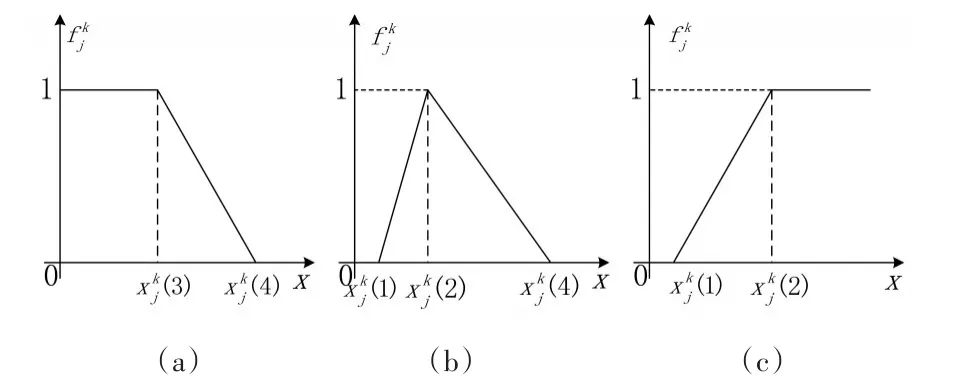
圖2 特殊情況下白化權函數(shù)圖像

對于上述各種類型的白化權函數(shù)，其表達式如下所示［10］。

由臨界值的定義可以得到權系數(shù)的定義，若表示評估指標j關于k子類的臨界值，則：

4 航空裝備可靠性評估模型的建立與應用

4.1 數(shù)據(jù)處理

通過收集數(shù)據(jù)，得到某團某一型航空裝備年度各可靠性指標數(shù)據(jù)如表1所示。

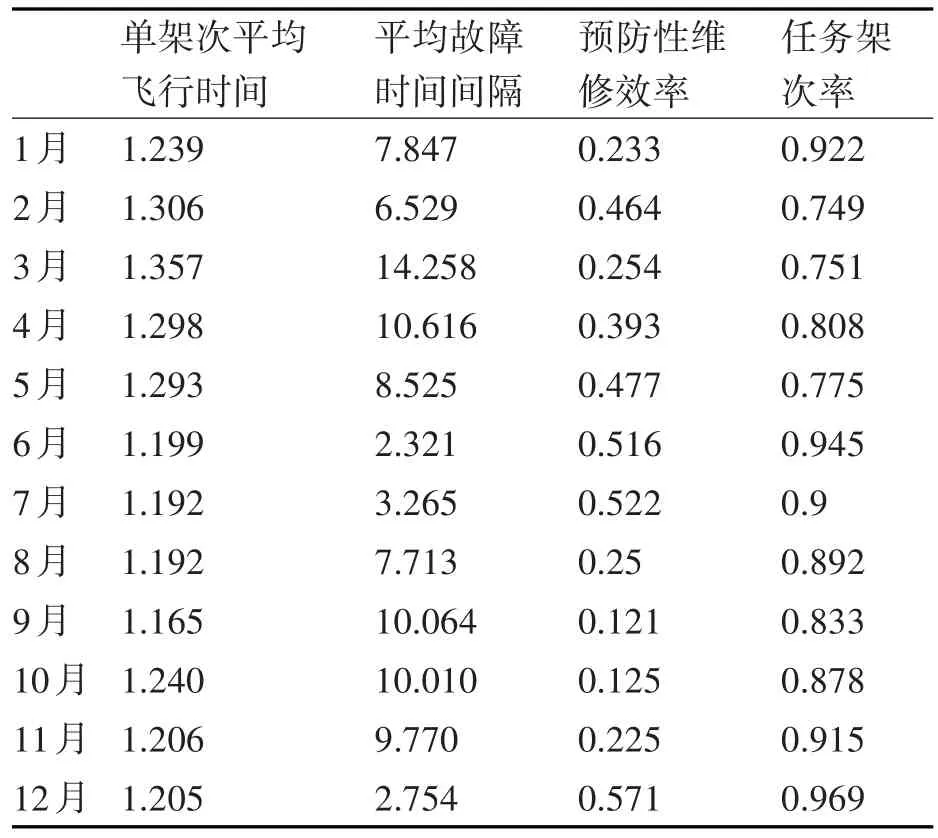
表1 航空裝備可靠性評估數(shù)據(jù)

根據(jù)灰色聚類法的使用要求，可以發(fā)現(xiàn)，在此選擇的四個指標，其評價標準都是值越大越好的，滿足了灰色聚類指標意義必須相同的使用要求，但是由于數(shù)據(jù)的量綱并不相同，且存在較大差距，需要進行進一步的處理。

數(shù)據(jù)調(diào)整對數(shù)據(jù)采用如下的標準化方法［12］：

先使用下式將原始樣本數(shù)據(jù)轉(zhuǎn)化為較小的數(shù)值。

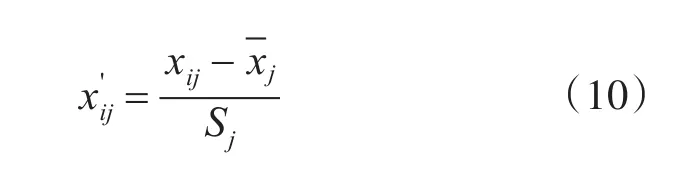
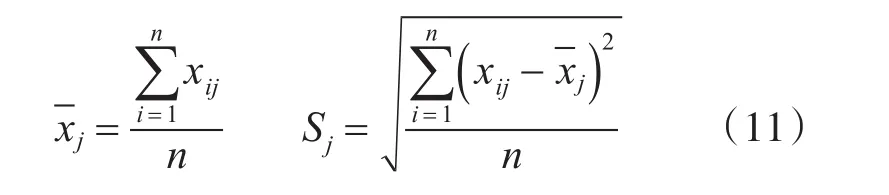
之后，將前一步得到的數(shù)值再次進行轉(zhuǎn)化，將數(shù)值結(jié)果落在區(qū)間［0，1］內(nèi)。

數(shù)據(jù)標準化之后的結(jié)果如表2所示。

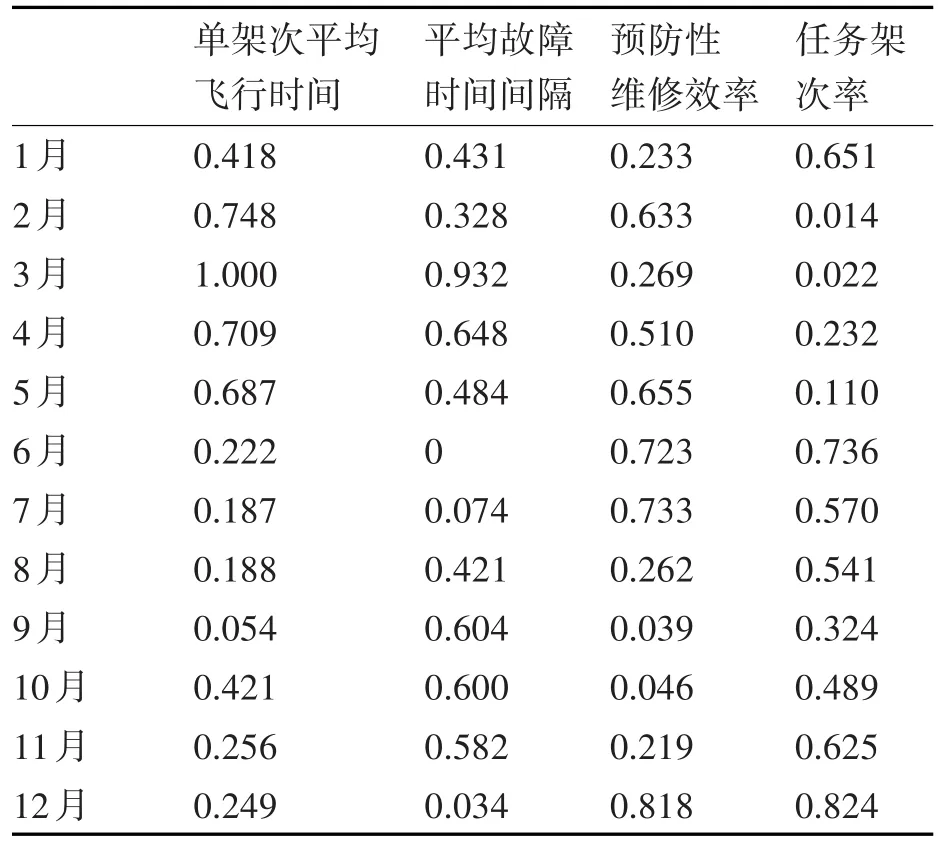
表2 標準化處理后的可靠性指標數(shù)據(jù)

4.2 可靠性評估模型的建立與實際應用

將灰類訂為5個，從高到低分別為V，IV，III，II，I，依次代表很好、較好、中等、一般、較差，將5個灰類按照正態(tài)分布模型進行分段，使這5個指標所對應的范圍能夠最大限度地將所有數(shù)據(jù)包含在內(nèi)，獲得評估灰類表如表3所示。

表3 評估指標灰類表（按原始數(shù)據(jù)分段）

為便于表示，單架次飛行時間、平均故障時間間隔、預防性維修效率、任務架次比例分別用x1～x4表示，通過表2中所示的數(shù)據(jù)來訓練評估模型。

進一步精確范圍，并使用之前的標準化方法計算之后，獲得表5中的結(jié)果。

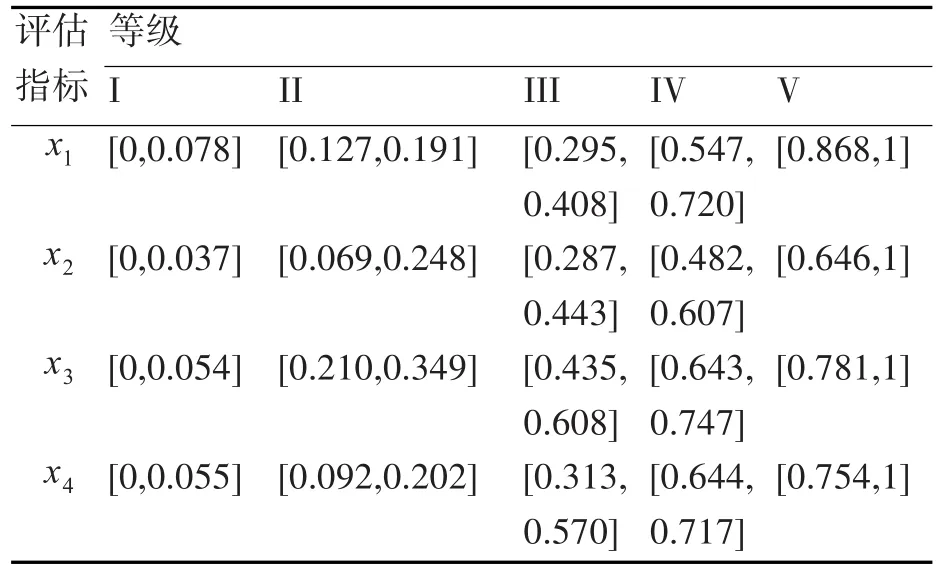
表4 評估指標灰類（按標準化數(shù)據(jù)分段）

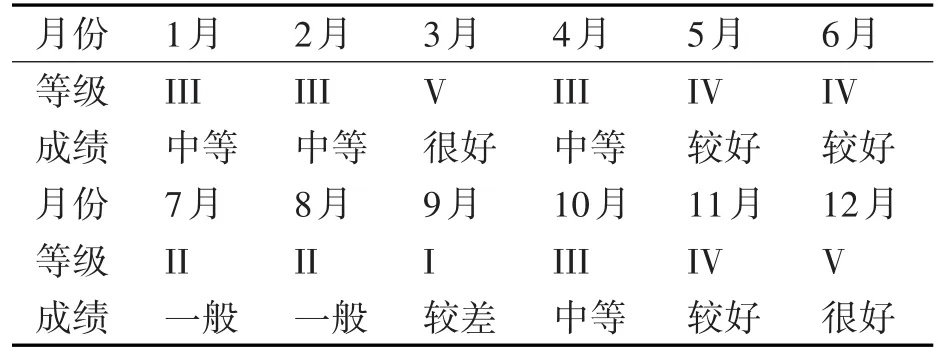
表5 可靠性評估結(jié)果

由表4給出的范圍可以得到20個白化權函數(shù)，確定函數(shù)基本形式的方法是［12］：

1）若該灰類內(nèi)元素越大越符合該灰類的要求，則采用上限測度白化權函數(shù)。

2）若該灰類內(nèi)元素越小越符合該灰類的要求，則采用下限測度白化權函數(shù)。

3）若灰類內(nèi)元素取白化值將圍繞著某小區(qū)域內(nèi)元素左右遞減，采用典型白化權函數(shù)。

4）若灰類內(nèi)元素取白化值圍繞某一點左右遞減，那么就采用適中測度函數(shù)。

通過以上的規(guī)則，得到對象j關于白化權函數(shù)圖像如圖3所示。

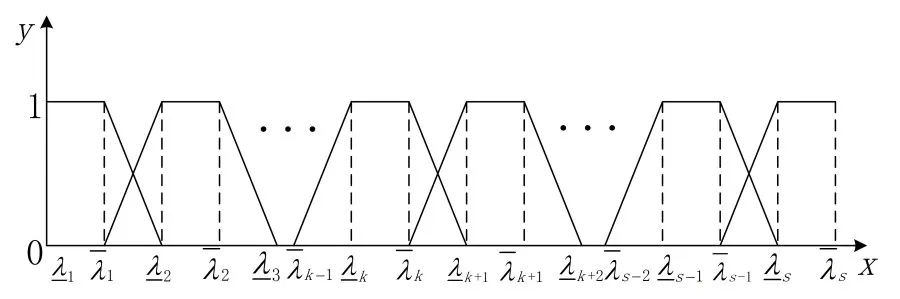
圖3 白化權函數(shù)示意圖

同時也可以由表4獲得指標j關于灰類k的臨界值矩陣Λ，進一步得到指標j關于灰類k的權系數(shù)矩陣Η，兩個矩陣如下所示：

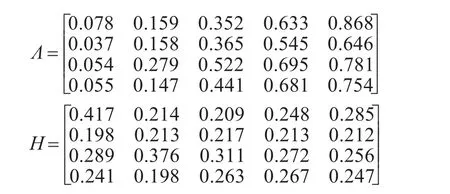
再可以通白化權函數(shù)組以及表3中的數(shù)據(jù)計算聚類系數(shù)矩陣Σ，由聚類系數(shù)矩陣根據(jù)灰類判定條件來判斷對象屬于哪一個灰類，進而就可以得出該當年各個月份的可靠性等級。

計算所得系數(shù)矩陣Σ如下所示，得到的可靠性等級如表6所示。

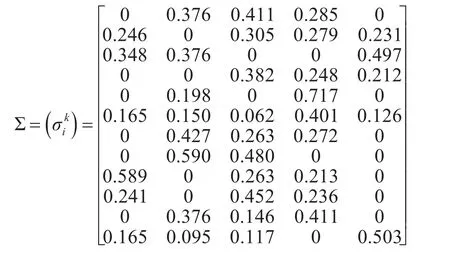
從計算結(jié)果可以發(fā)現(xiàn)，該團一年中航空裝備的可靠性評價結(jié)果達到良好以上的有3月、5月、6月、11月、12月，但是有的月份可靠性評估等級較低，如9月份出現(xiàn)了“較差”的評估等級，出現(xiàn)這種情況，就需要即時查找原因，對當月故障情況與飛行情況及時進行分析。

5 結(jié)語

本文主要研究灰色變權聚類，結(jié)合部隊實際建立了航空裝備可靠性評估模型，通過白化權函數(shù)合理分配每個評估指標的權重，再由計算所得的聚類系數(shù)矩陣獲得相應的評價結(jié)果。通過實際測試發(fā)現(xiàn)該模型具有較高的可操作性，以直觀的方式呈現(xiàn)評價結(jié)果，且評價結(jié)果也較為客觀。基于灰色變權聚類的航空裝備可靠性評估模型，為裝備的可靠性評估提供了一種新的思路，能夠幫助機務人員發(fā)現(xiàn)哪些月份中航空裝備的可靠性較低，并及時找出導致裝備可靠性降低的原因。