三體船波浪增阻與縱向運動數值模擬及試驗研究

李昂， 李云波

(1.哈爾濱工程大學 船舶工程學院，黑龍江 哈爾濱 150001； 2.上海海事大學 海洋科學工程學院，上海 201306)

三體船在合理的主片體布局下，相比于單體船和雙體船，在中高航速下具有良好的阻力性能。而在耐波性方面，由于2個側片體的存在，三體船也具有優良的穩定性以及耐波性能，成為極具應用前景的新船型。海上航行的船舶通常會遭遇波浪，船舶在波浪中的增阻會導致主機功率的增加。如何精確地預報船舶在波浪中的增阻非常重要。在過去的幾十年里，波浪增阻以及船舶運動問題已經通過模型試驗以及數值計算方法進行了廣泛的研究。

模型試驗方法包括對60系列[1]和S175集裝箱船[2]、Wigley船型[3]以及KVLCC2船型[4]的波浪增阻問題的研究。對于三體船型波浪增阻的試驗研究相對較少。基于勢流理論方法研究波浪增阻問題可以主要分為遠場方法[5]、近場方法[6]以及Rankine源法[7]。隨著計算機技術的迅速發展，CFD技術在預報船舶波浪增阻以及運動方面得到廣泛的應用，基于粘流理論的CFD數值計算方法考慮了粘性效應，能夠計算船舶的大幅運動。國內外研究學者對單體船型進行了大量的CFD計算研究[8-11]，分析了航速、波浪周期、波幅等參數對波浪增阻及運動的影響。吳乘勝等[12]對高速三體船波浪中運動與增阻進行了數值計算研究，分析了側片體對主船體阻力增加的影響。陳悅等[13]對高速三體船在規則波中的波浪增阻及縱向運動進行了數值仿真研究，并通過與模型試驗結果進行對比驗證其方法的有效性。國內外對于航速、波陡等參數變化對三體船迎浪規則波中運動帶來的非線性的影響研究較少。

本文針對某三體船型在迎浪規則波中的波浪增阻以及縱向運動進行了數值計算和模型試驗研究，分析了三體船不同航速下迎浪規則波中波浪增阻和縱向運動響應特性。采用重疊網格和運動域網格方法分別對不同航速下三體船波浪增阻及縱向運動響應進行了數值計算，并通過與船模水池試驗結果進行對比分析，探討了不同網格劃分方法對數值計算結果的影響。研究了不同波陡波浪參數對三體船波浪增阻及縱向運動的非線性影響。

1 CFD數值計算方法

1.1 基本控制方程

計算中整個流場屬于三維、兩相、黏性的不可壓縮流體流動。對于湍流的模擬采用雷諾平均法，控制方程為：

(1)

(2)

(3)

1.2 CFD數值波浪水池

為了模擬三體船周圍流場，考慮到計算效率以及計算精度，本文建立了圖1所示的長方體計算域。具體計算域的參數設置為：船前1倍船長，船艉3倍船長，船側1.5倍船長，自由液面以上1倍船長，自由液面以下2倍船長。整個流體計算域關于三體船中體中縱剖面對稱，將三體船中體中縱剖面所在平面取為對稱平面，側邊邊界條件也設置為對稱平面。入口、頂部以及底部邊界條件設置為速度進口，出口邊界條件設置為壓力出口。為了避免波浪傳播到計算域尾端產生回流而影響整個流場的分布，對波浪進行消波處理，消波區的長度設置為1倍船長。

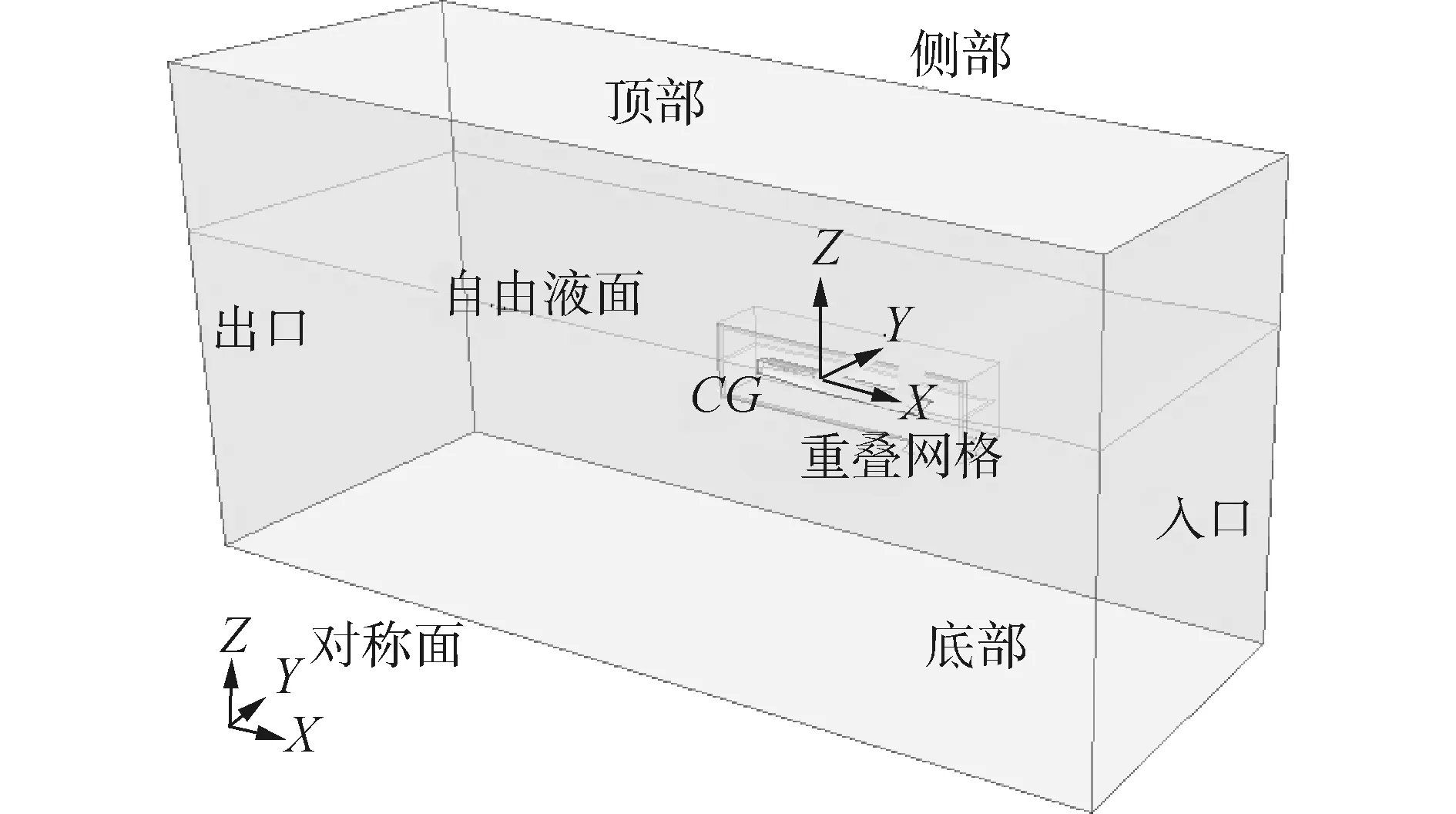
圖1 計算域及邊界

1.3 數值計算網格模型

網格劃分對于模擬細節流場的計算精度以及迭代的收斂性具有較大影響。本文使用重疊網格方法和運動域網格方法對三體船不同航速下靜水中阻力及迎浪規則波中縱向運動進行了數值計算。

重疊網格是將物體各運動單元單獨劃分網格，再嵌入到另一套網格當中，各個子域網格存在重疊、嵌套或覆蓋關系，流場信息通過插值的手段在重疊區域邊界進行交換和匹配。在運動域網格方法中，整個流體計算域被處理為一個運動的整體。圖2為船舶運動過程中，重疊網格以及運動域網格示意圖。可以發現，三體船航速較高時，縱向運動響應幅值較大導致自由液面網格變形，導致數值計算精度下降。

圖2 重疊網格及運動域網格示意

重疊網格重疊域的尺寸設置為：船前0.15倍船長，船側、船后及水線以上和水線以下分別為0.2倍船長。為了能夠精確捕捉自由液面，在自由液面處進行了網格加密。對于不同波長下三體船波浪增阻及運動的數值計算，計算域的網格劃分也有所不同。對于較短波長，對自由液面以及船體周圍進行網格加密。圖3和圖4所示是當傅汝德數Fr為0.353時，波長船長比λ/L=0.50和λ/L=1.60時自由面的網格示意圖。在整個波長范圍內的數值計算當中，保證單位波長下70～100個網格，單位波高下14～20個網格。

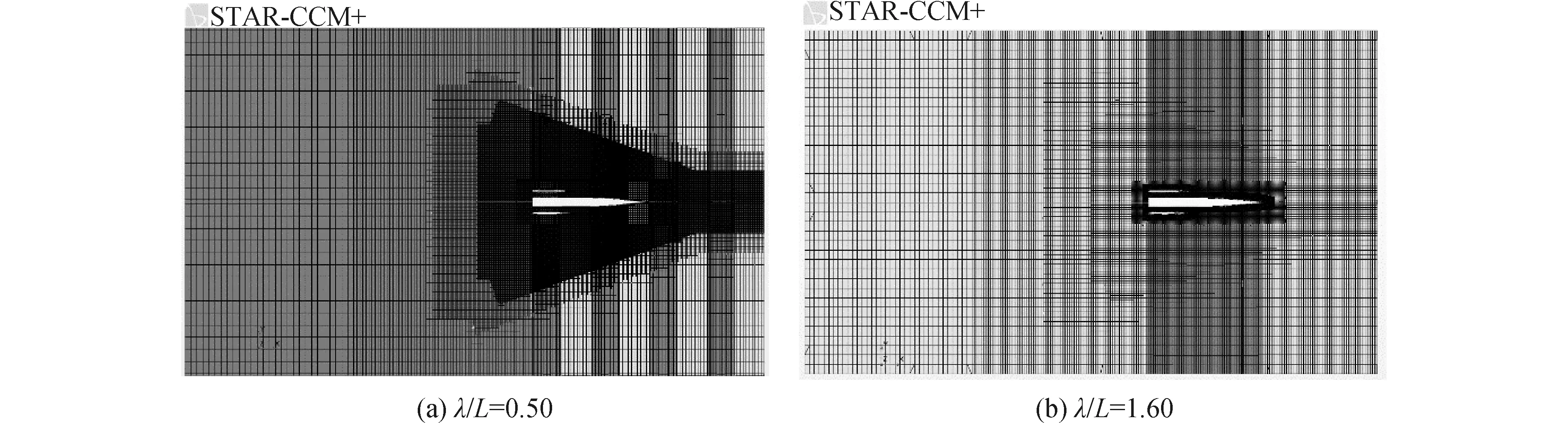
圖3 自由面網格劃分示意圖

2 船模水池試驗

2.1 三體船模型參數

三體船模型的主尺度參數如表1所示。其模型示意圖如圖4所示。

表1 三體船模型主尺度參數

圖4 三體船模型示意

2.2 波浪參數及船模試驗工況

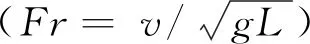
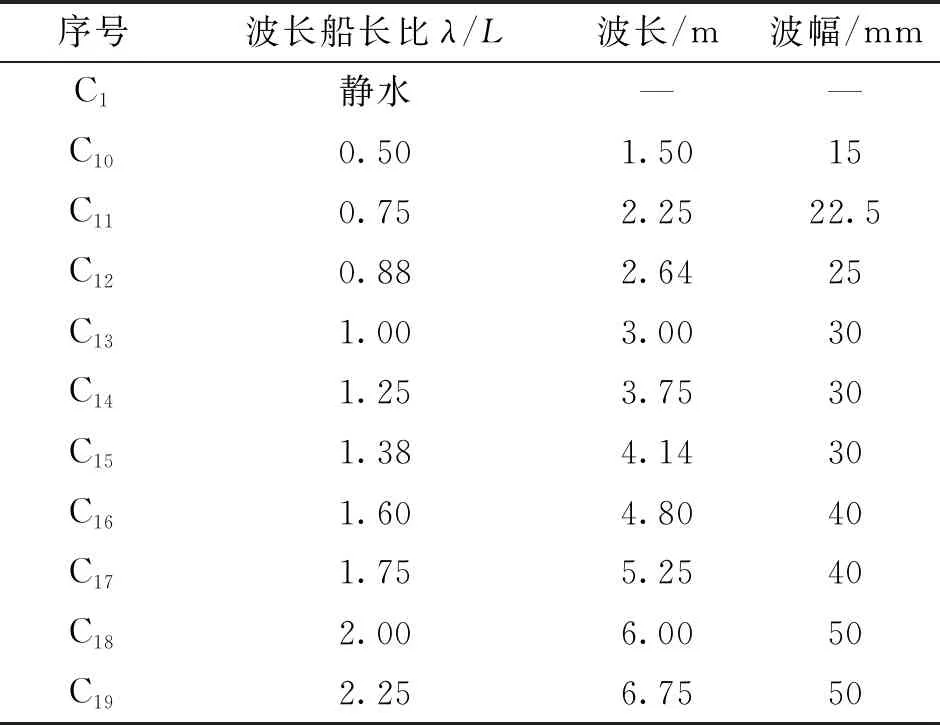
表2 波浪參數(Fr=0.628)

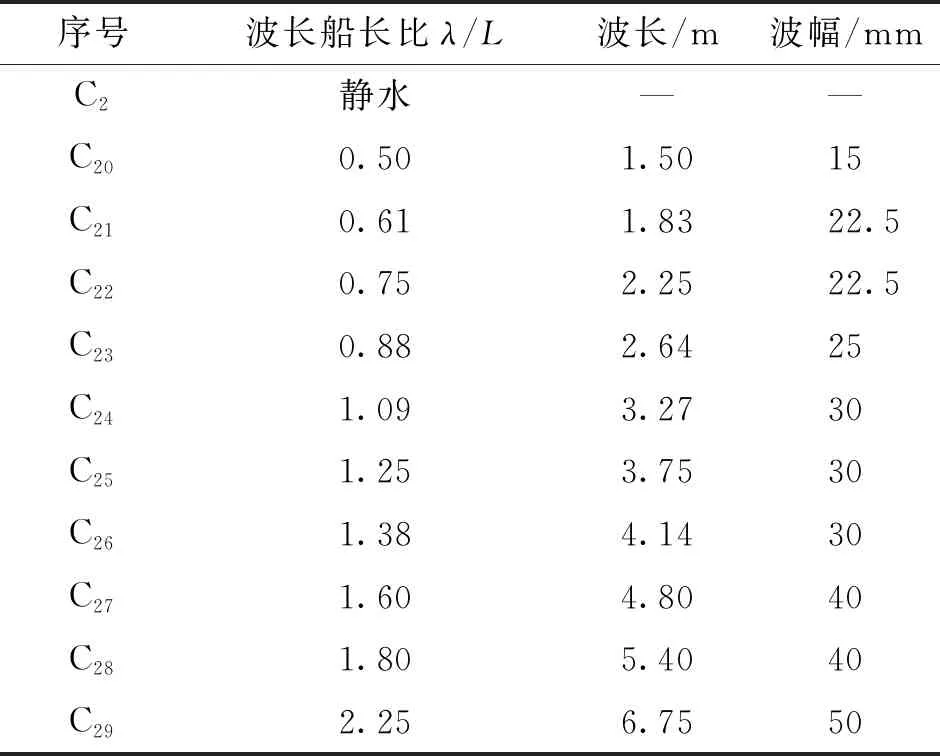
表3 波浪參數(Fr=0.353)

3 數值計算和船模試驗結果分析

3.1 三體船靜水阻力

為了研究不同網格劃分方法對三體船迎浪規則波中波浪增阻及縱向運動響應的影響，本文首先使用重疊網格方法和運動域網格方法對三體船靜水阻力進行了數值計算，得到三體船不同航速下法靜水阻力計算結果。靜水阻力數值計算結果同模型試驗結果對比見表4和表5。

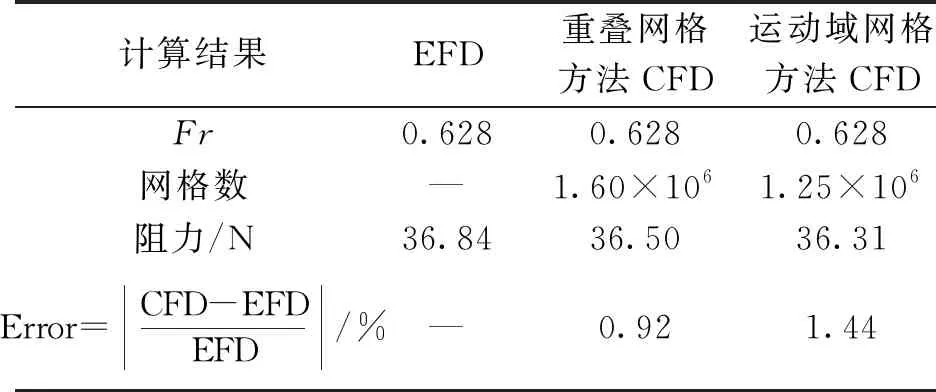
表4 三體船靜水阻力(Fr=0.628)

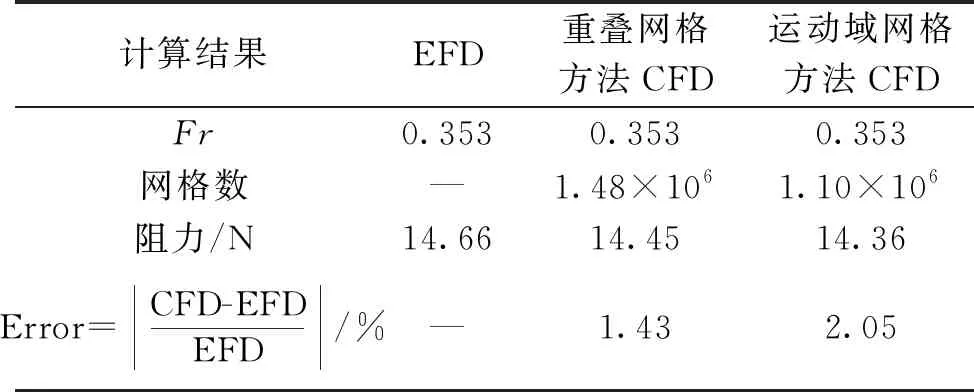
表5 三體船靜水阻力(Fr=0.353)

表4所示是使用重疊網格方法和運動域網格方法得到的三體船傅汝德數0.628航速下靜水阻力數值計算結果和模型試驗結果。表5所示的是使用重疊網格方法和運動域網格方法數值計算得到的三體船傅汝德數0.353航速下靜水阻力結果和模型試驗結果。有研究表明，船體表面邊界第1層網格的無量綱厚度y+值取100可取得較為理想的計算結果[14]。圖5所示的是本文研究中三體船船體表面邊界第1層網格的無量綱厚度y+沿主、側體的分布圖。整個三體船船體表面邊界第1層網格的無量綱厚度y+值在60～140。

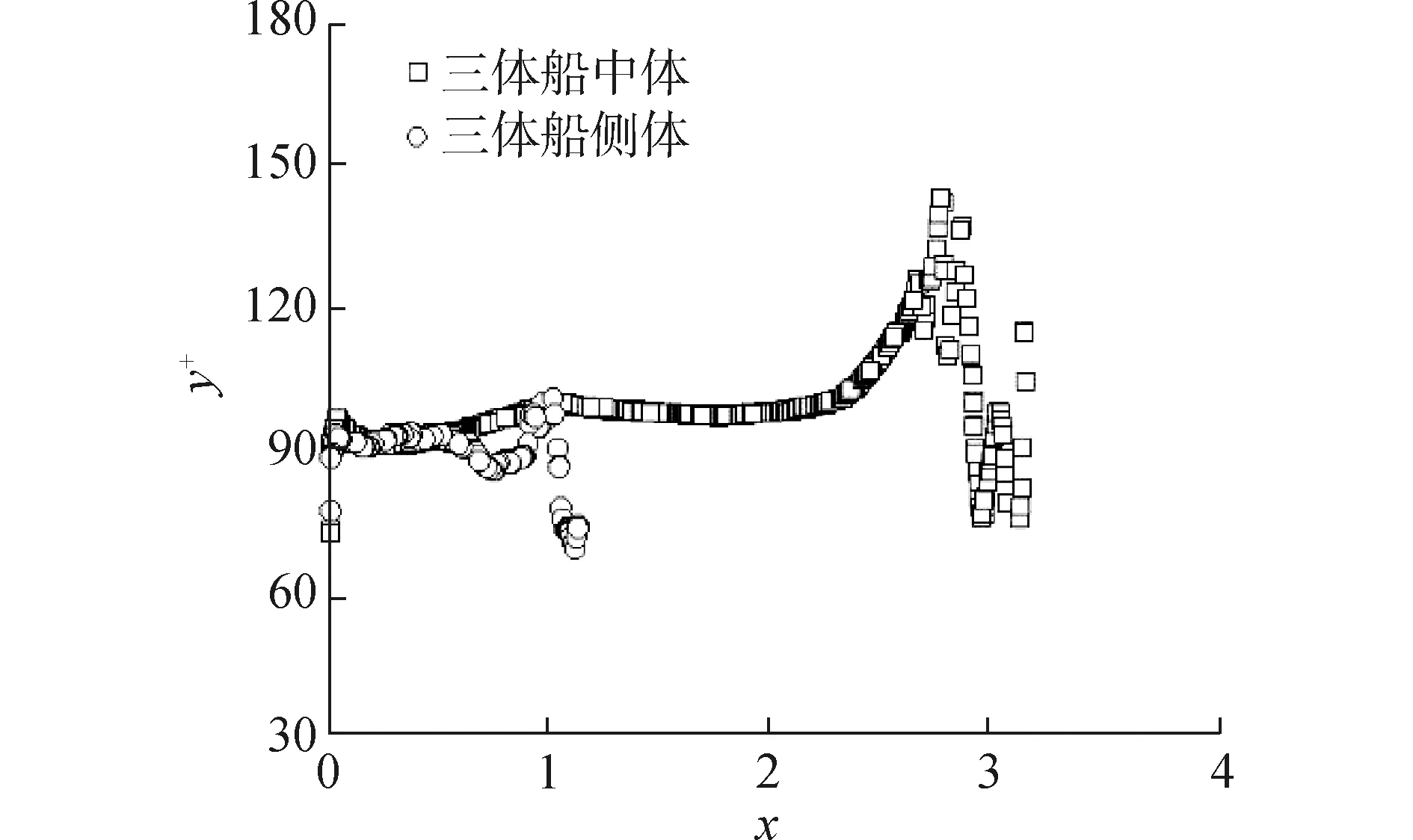
圖5 船體表面y+分布

經過分析比較不同傅汝德數下三體船靜水阻力數值計算結果與試驗結果，重疊網格以及運動域網格方法都可以較為準確地計算三體船不同傅汝德數下的靜水阻力。使用重疊網格方法得到的三體船靜水阻力計算結果在不同傅汝德數相比于運動域網格方法與模型試驗結果誤差更小。

3.2 數值造波及三體船波浪增阻與縱向運動

為了得到三體船的波浪增阻及縱向運動響應，并探討不同網格劃分方法對數值計算結果的影響。本文使用重疊網格方法和運動域網格方法數值計算了三體船在不同航速下迎浪規則波中的運動響應以及總阻力。通過計算不同波浪參數條件下三體船的總阻力與靜水阻力的差值，得到三體船在迎浪規則波中運動時的波浪增阻。為了驗證數值計算域中所造波浪的精度，在三體船船前0.5倍水線長處設置波高監測點[15]，圖6所示的是波長船長比λ/L=1.38時，波高監測點數值計算得到的波浪幅值時歷曲線。經過傅里葉級數表達得到的一階波浪幅值為0.028 4 m，與理論波幅的誤差為5.33%。

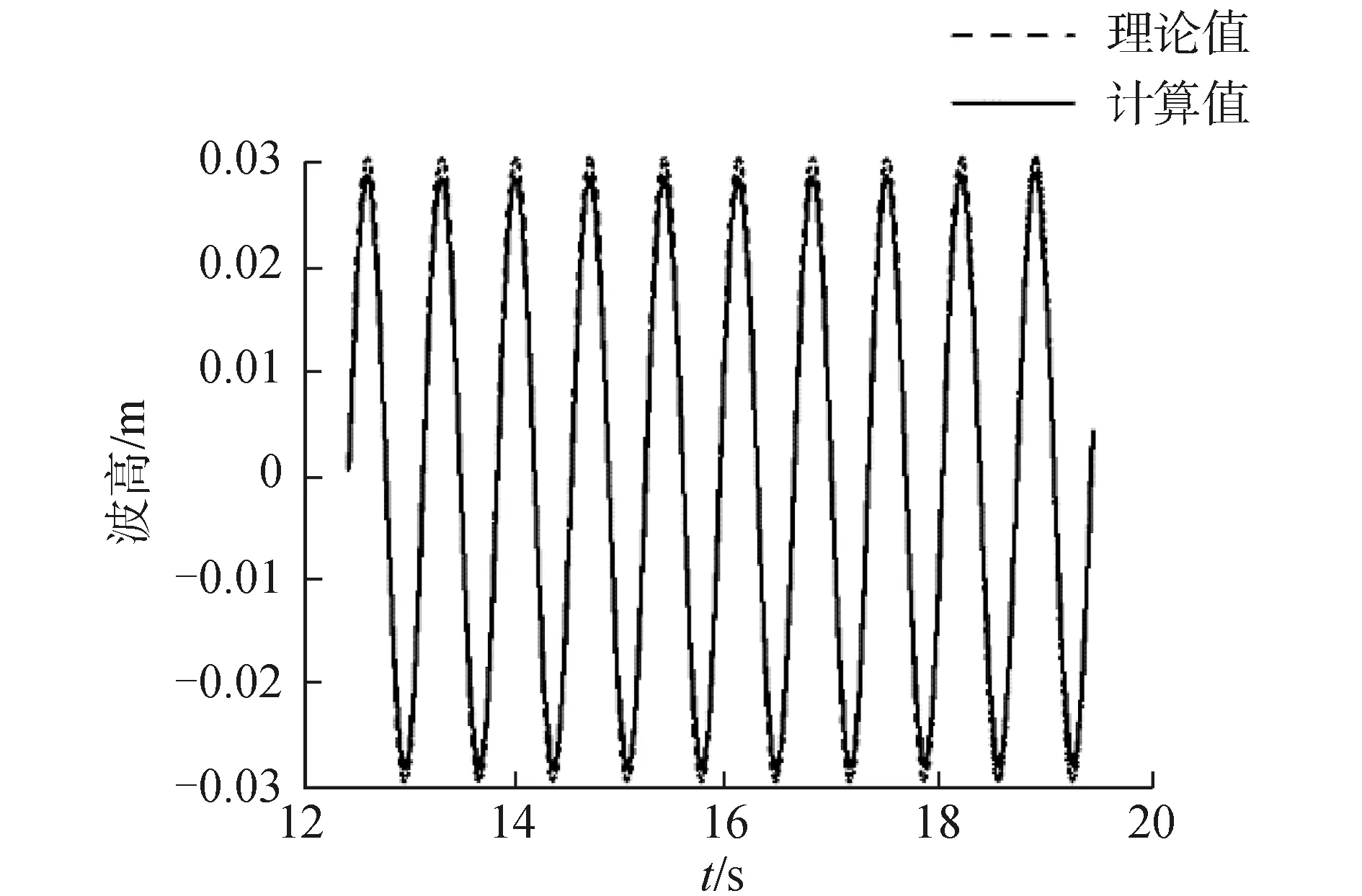
圖6 波高檢測點波幅時歷曲線

使用重疊網格方法以及運動域網格方法數值計算得到的三體船不同航速下升沉、縱搖運動響應曲線以及波浪增阻計算結果與模型試驗結果如圖7～圖12所示。

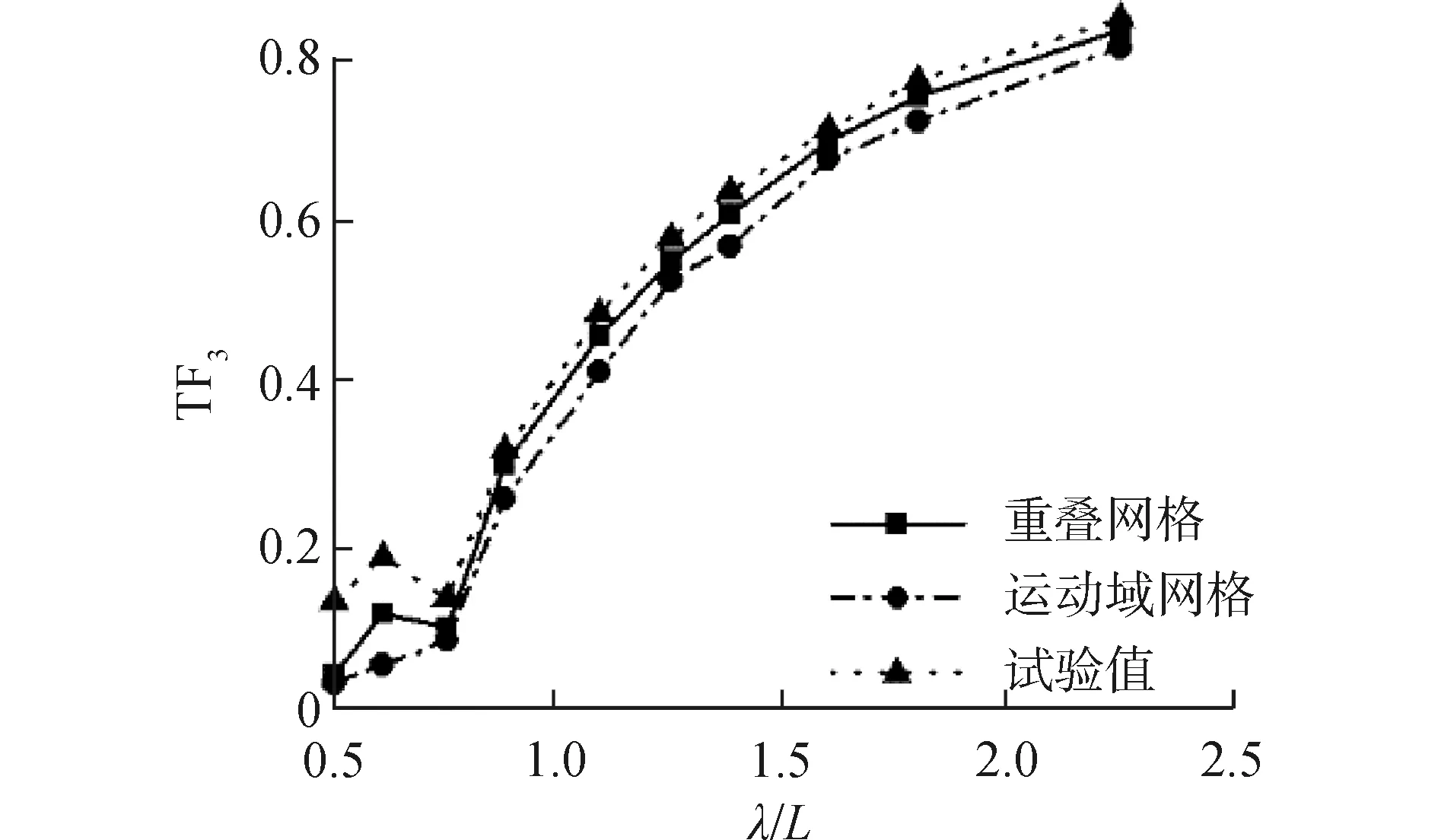
圖7 較低航速三體船升沉運動響應曲線(Fr=0.353)

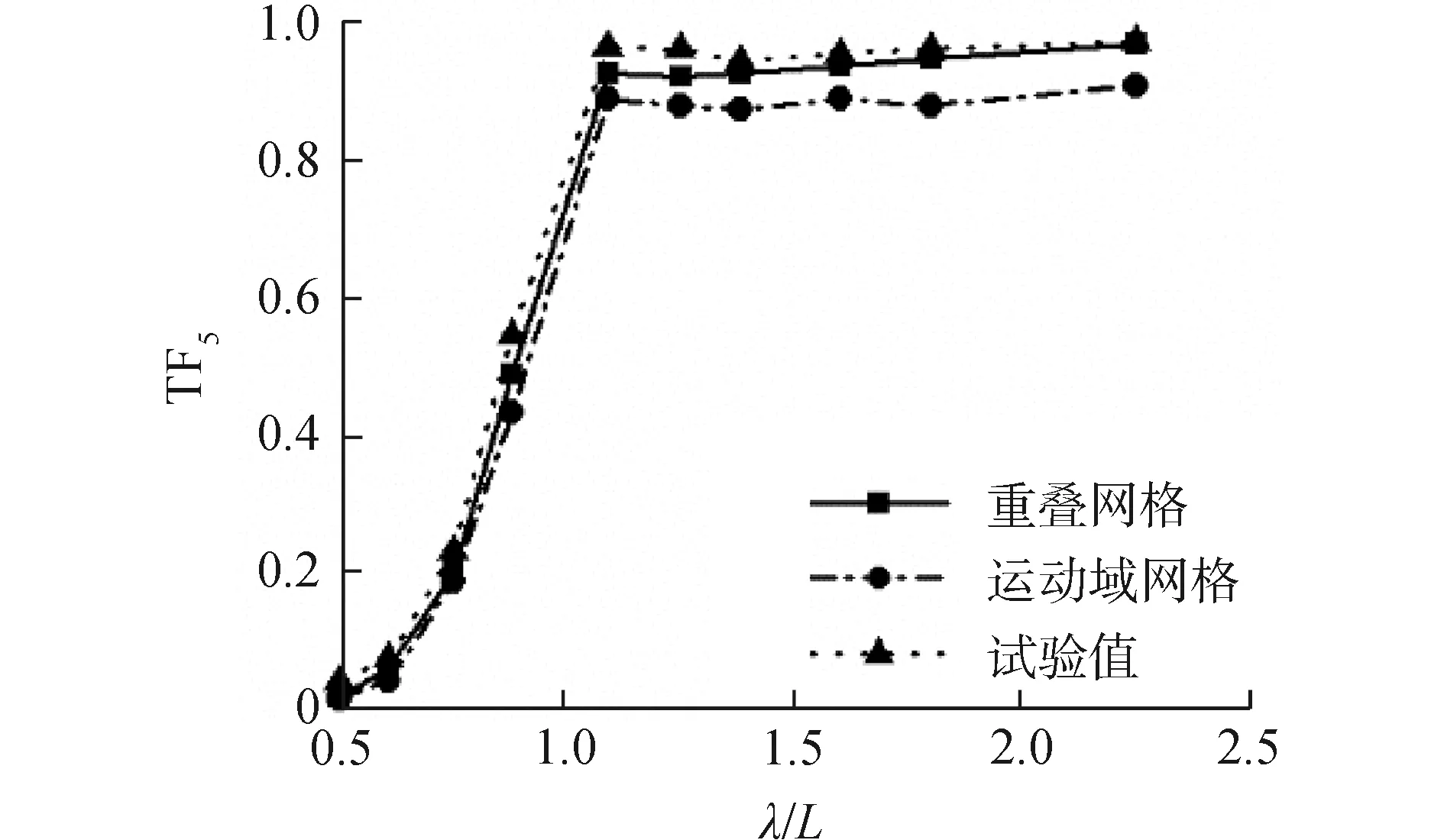
圖8 較低航速三體船縱搖運動響應曲線(Fr=0.353)

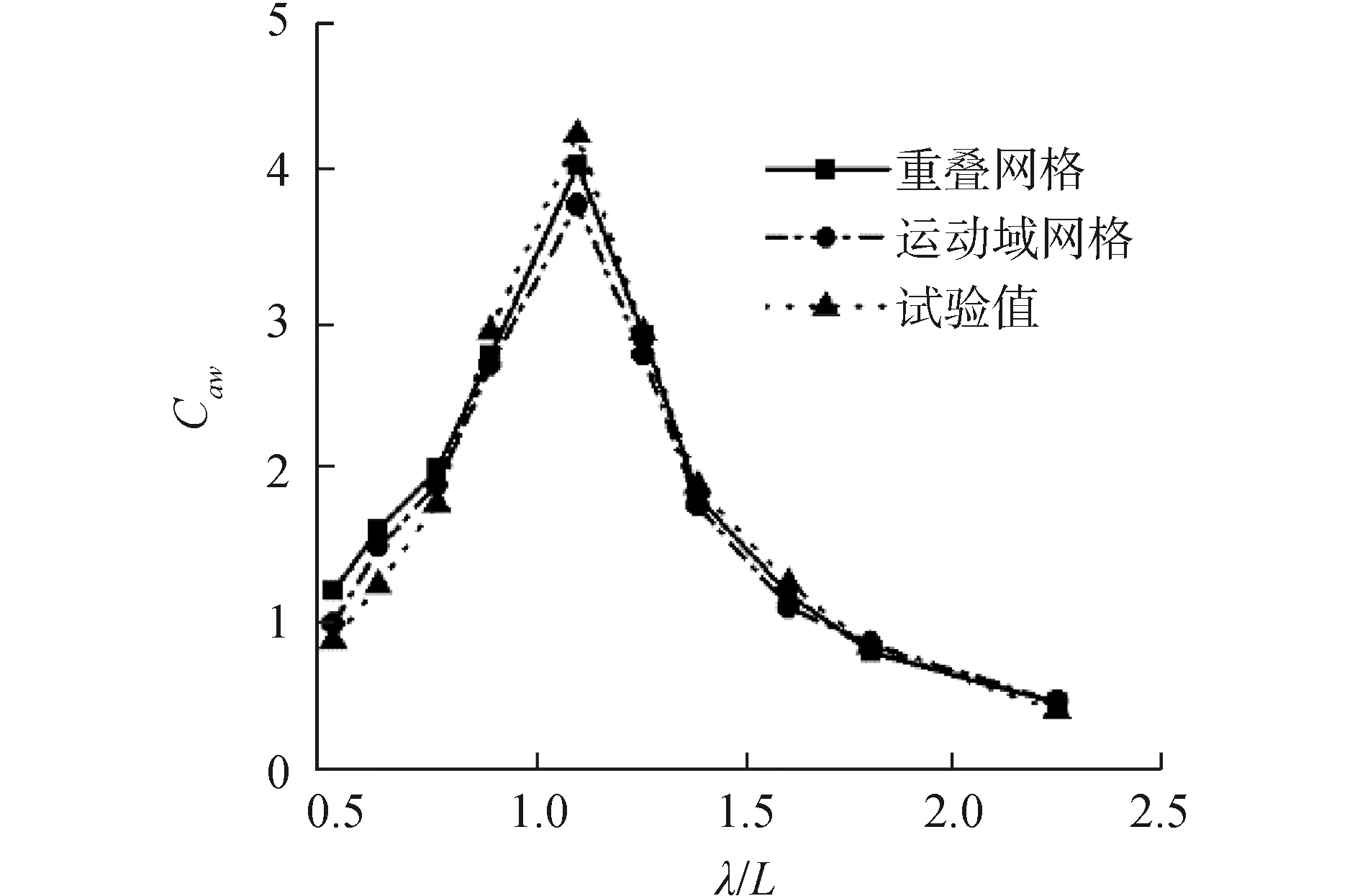
圖9 較低航速三體船波浪增阻曲線(Fr=0.353)

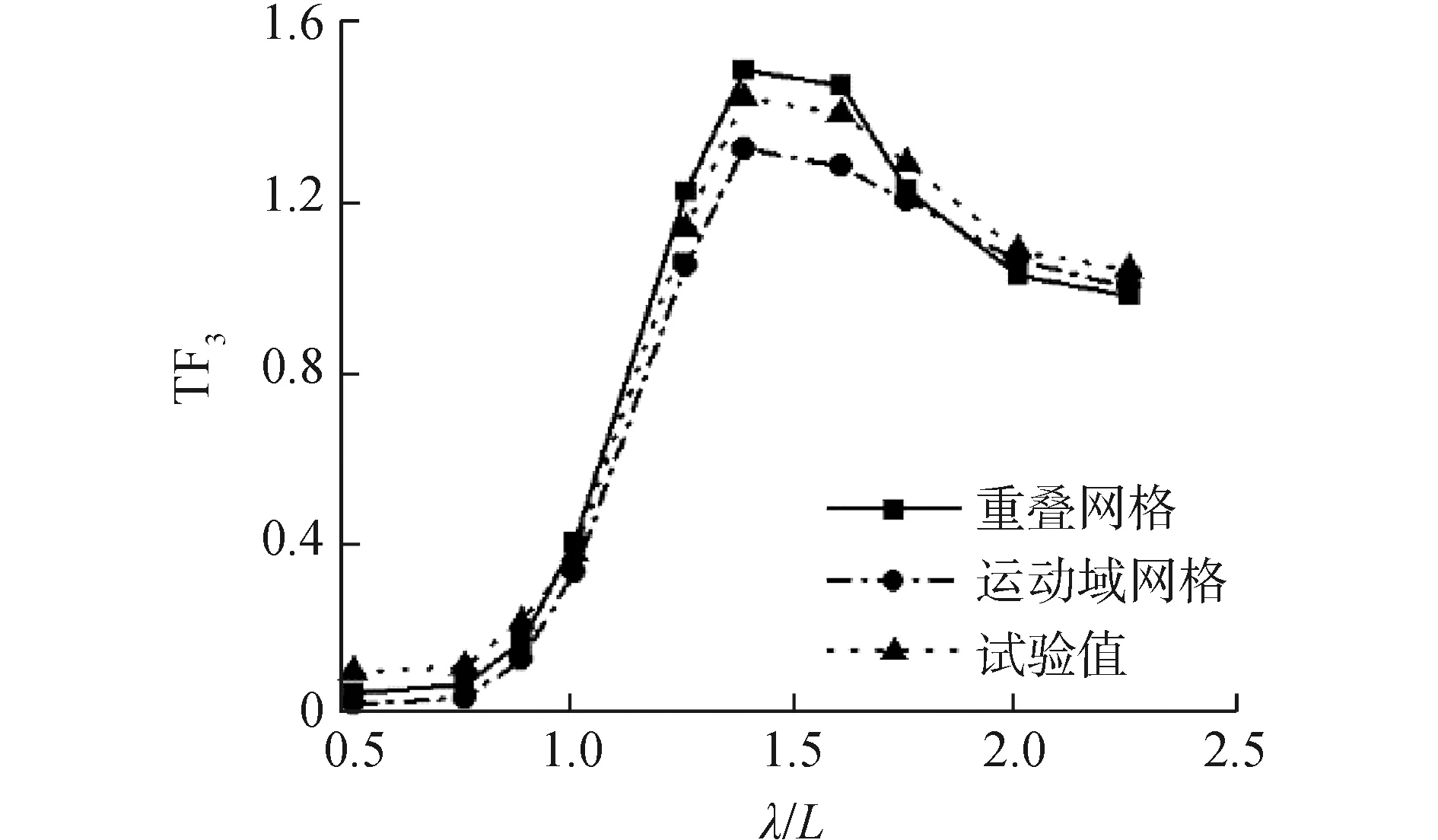
圖10 高速三體船升沉運動響應曲線(Fr=0.628)

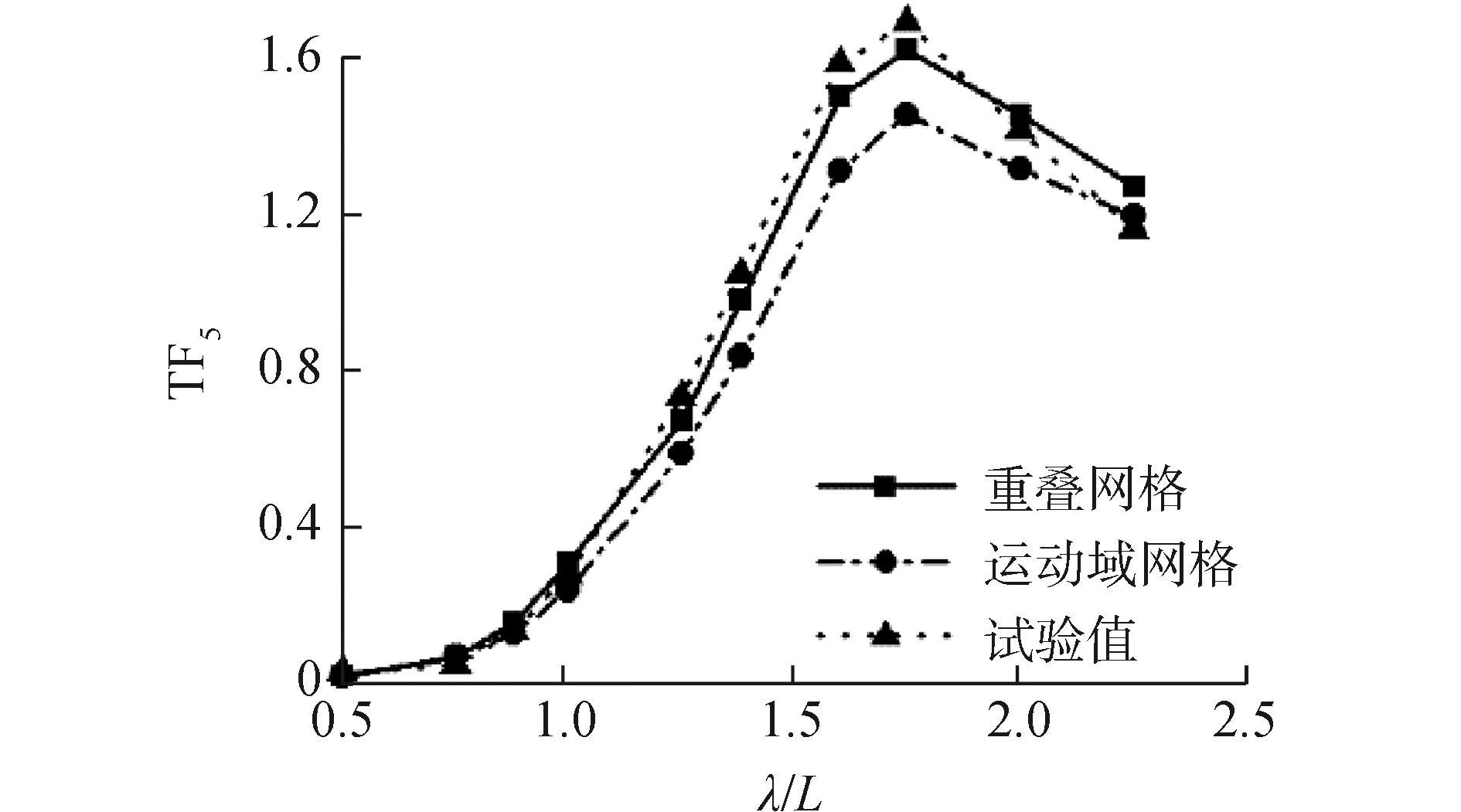
圖11 高速三體船縱搖運動響應曲線(Fr=0.628)

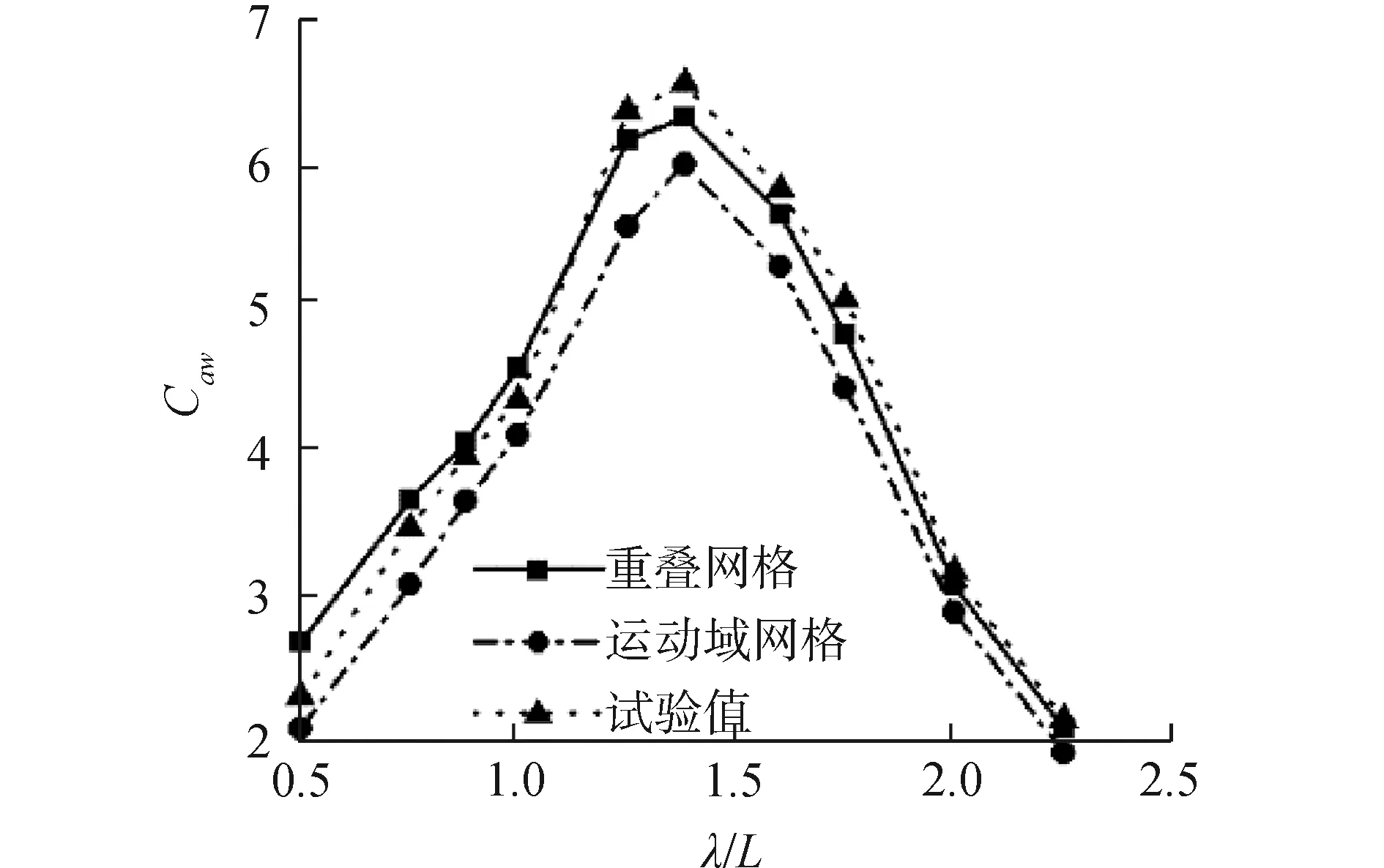
圖12 高速三體船波浪增阻曲線(Fr=0.628)

圖7～12分別表示三體船在迎浪規則波中數值計算和模型試驗的升沉、縱搖運動響應以及波浪增阻曲線。三體船迎浪規則波中升沉、縱搖運動響應的無因次化公式表示為：

(4)

(5)

式中：Za表示升沉運動響應幅值；φa表示縱搖運動響應幅值；ζa表示規則波波幅；k表示波數。

通過三體船在迎浪規則波中的總阻力減去三體船在靜水中的阻力，得到三體船在波浪中的增阻。波浪增阻的計算公式及其無因次化公式為：

(6)

(7)

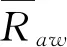
圖7～9表示的是傅汝德數為0.353時迎浪規則波中升沉、縱搖運動響應及波浪增阻。數值計算結果與船模試驗結果對比可見，使用重疊網格方法與運動域網格方法得到的三體船升沉、縱搖運動響應以及波浪增阻與船模水池試驗結果有相同的變化趨勢；使用運動域網格計算方法并沒有捕捉到在波長船長比λ/L=0.61附近出現的小峰值點；使用運動域網格計算方法得到的縱向運動響應幅值以及波浪增阻相比于重疊網格計算方法得到的縱向運動響應幅值及波浪增阻較小，重疊網格方法數值計算結果誤差更小。

圖10～12是傅汝德數為0.628時迎浪規則波中的升沉、縱搖運動響應及波浪增阻。由數值計算結果與船模試驗結果對比可見，使用重疊網格方法與運動域網格方法數值計算得到的三體船升沉、縱搖運動響應以及波浪增阻與船模水池試驗結果有著相同的變化趨勢，在運動幅值出現的波長船長比(λ/L=1.60)附近的共振區內，由于三體船縱向運動響應幅值較大，運動域網格計算方法中自由面網格的變形較大，數值計算誤差相對較大。得到的升沉、縱搖運動響應幅值相比于重疊網格計算方法較小，使用重疊網格計算方法得到的數值計算結果誤差更小。從三體船波浪增阻曲線來看，在整個波長范圍內，使用運動域網格計算方法得到的波浪增阻誤差較大。綜上，重疊網格方法更適于計算高航速三體船縱向運動響應及波浪增阻。因此，后續探討波陡對三體船波浪增阻及縱向運動的影響時，均采用重疊網格計算方法。

3.3 波陡對三體船波浪增阻及縱向運動的影響

本文對λ/L=0.50和λ/L=1.60波長、傅汝德數0.353和0.628，研究了三體船波浪增阻和縱向運動與波陡(H/λ)的關系，具體波浪參數見表6和表7。數值計算得到的不同航速、不同波長下三體船波浪增阻及縱向運動響應曲線以及波陡對三體船波浪增阻及縱向運動影響見圖13～18。

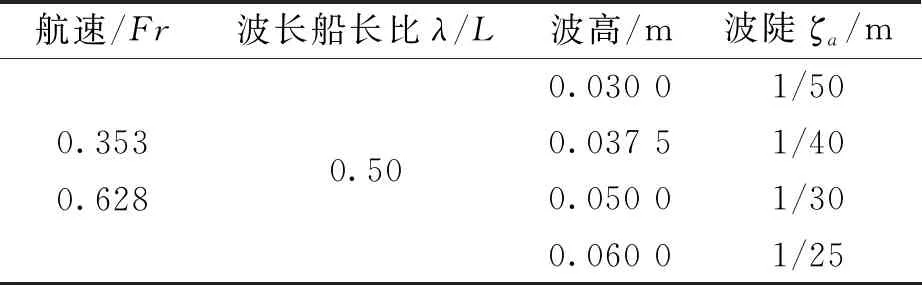
表6 波浪參數(λ/L=0.50)

表7 波浪參數(λ/L=1.60)

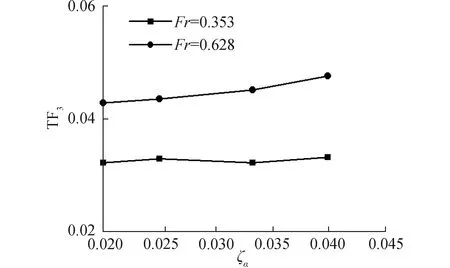
圖13 小波長不同波陡升沉運動響應曲線

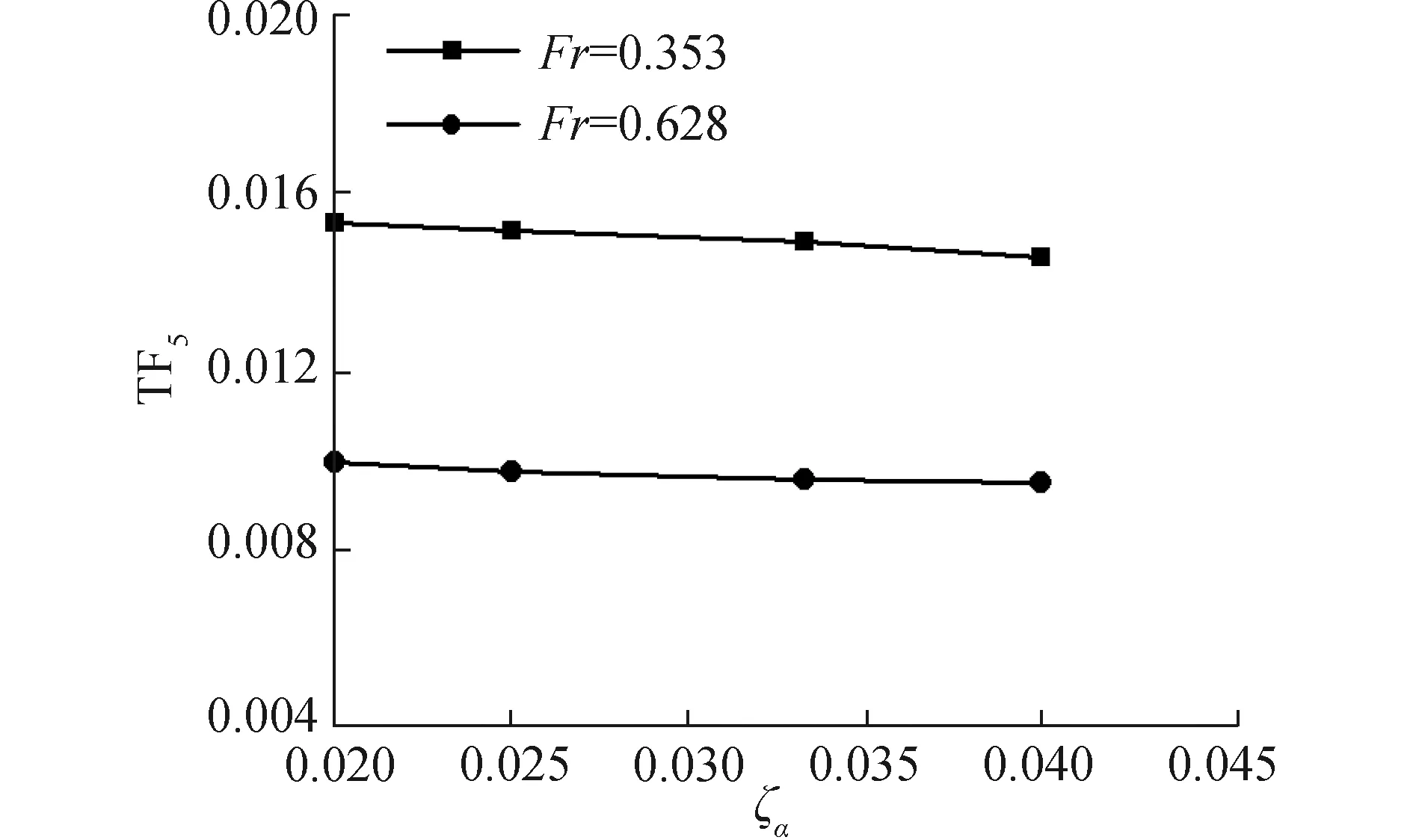
圖14 小波長不同波陡三體船縱搖運動

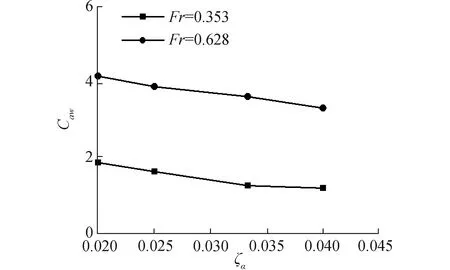
圖15 小波長不同波陡三體船波浪增阻曲線

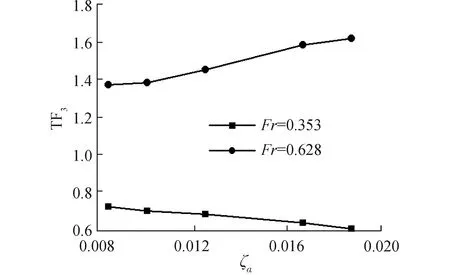
圖16 大波長不同波陡升沉運動響應曲線

圖13～15表示的是傅汝德數為0.353和0.628下短波λ/L=0.50中三體船升沉、縱搖運動響應以及波浪增阻隨波陡變化的數值計算結果。由圖13可得，三體船在較低航速升沉運動響應隨波陡的增加變化不大，較高航速升沉運動響應結果隨波陡的增加而增加，表現出高航速下的非線性；圖14表示在不同航速下，三體船縱搖運動響應隨波陡增加的變化不大，有減小的趨勢。高航速三體船在短波λ/L=0.50中波陡變化并沒有對縱搖運動產生強烈的非線性影響；由圖15可見，高航速時，三體船的波浪增阻系數較大，隨著波陡的增加，波浪增阻系數在不同航速下都有減小的趨勢，表現出明顯的非線性特征。

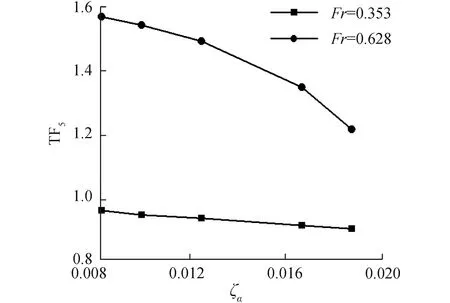
圖17 大波長不同波陡縱搖運動響應曲線

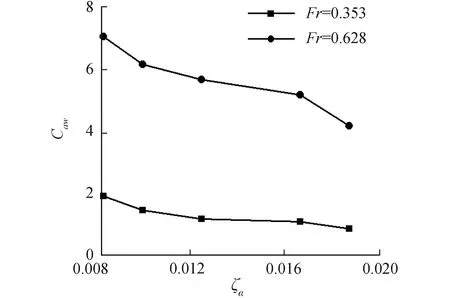
圖18 大波長不同波陡波浪增阻曲線

圖16～18表示的是傅汝德數為0.353和0.628航速下得到的在長波λ/L=1.60中三體船升沉、縱搖運動響應以及波浪增阻隨波陡變化的數值計算結果。圖16表示三體船在較低航速，升沉運動響應隨波陡的增加有減小的趨勢，相比于短波λ/L=0.50非線性增強，對于較高航速，升沉運動響應結果隨波陡的增加而增加，表現出高航速下的非線性，并相對于短波λ/L=0.50非線性更加明顯；圖17表示三體船在較低航速，縱搖運動響應結果隨波陡的增加有減小的趨勢，同短波λ/L=0.50類似，非線性特征并不明顯；對于較高航速時，縱搖運動響應隨著波陡的增加有明顯的減小，表現出強烈的非線性特征；圖18表示高航速時，三體船的波浪增阻系數較大，隨著波陡的增加，波浪增阻系數在不同航速下均有減小的趨勢，表現出較強的非線性，相比于短波λ/L=0.50，非線性特征更加明顯。

4 結論

1)重疊網格數值計算方法更適用于計算三體船高航速時迎浪規則波中的增阻及運動；

2)三體船在高航速時波浪增阻及縱向運動的非線性特征明顯；

3)波陡變化帶來的非線性影響在長波波浪條件下更加明顯。