基于改進BP 的電力通信蓄電池壽命預測研究*

施 健 魏訓虎 徐士元 陳克朋

（南京南瑞信息通信科技有限公司 南京 210003）

1 引言

電力通信作為保障電網安全穩定運行的一類基礎性重要設施，其在安全性和可靠性方面有著特殊的要求。由于通信設備的供電可能存在著電壓不穩或不可用等潛在隱患，為保障通信設備以及上面所承載的電網業務正常運轉，通常會配備閥控鉛酸蓄電池，以此作為保障通信設備可靠運行的后備電源系統［1～3］。

然而在偏遠地區的變電站中，在運的蓄電池長期面臨著溫濕度環境變化大、長期處于浮充狀態，以及養護水平不到位等眾多不利因素的困擾，使得蓄電池的壽命常常達不到正常的使用年限。一旦某一單體蓄電池發生提前失效問題，會導致同一蓄電池組的其他單體蓄電池劣化速度加快，進而影響到蓄電池組的整體壽命與效能，最終可能引入容量不足、甚至蓄電池組開路等一系列故障，從而引發整個通信網絡中斷的重大事故［4～5］。隨著泛在電力物聯網的起興，提高現場蓄電池運行狀態的全息感知能力，科學預測出蓄電池剩余壽命，為科學養護蓄電池提供依據，已成為電力通信急需解決的技術難點和核心問題。

本文深入研究了循環使用過程中影響蓄電池壽命的各類客觀、主觀因素，在綜合實際容量、循環使用次數以及在整個蓄電池組中出力貢獻程度因素下，提出了以蓄電池壽命因子作為估算蓄電池實際容量的一個修正系統，以此提高估算精度，并在此基礎上構建了改進的蓄電池壽命估算模型。借助電力通信中長期積累的蓄電池單體電池與整組電池參數實時/在線監測與檢測數據、充放電實驗數據、動力環境數據等海量信息，分別利用Levenberg-Marquardt 法（trainlm）、共軛梯度法（traincgb）和擬牛頓方法（trainbfg）三種訓練函數進行比較并分析其估計效果，發現LM-BP 神經網絡算法的收斂速度最快。同時，針對傳統BP 神經網絡存在的易于陷入局部最小值的問題，本文提出了一種改進的BP神經網絡算法，經實際仿真驗證，利用改進的BP 神經網絡算法在對蓄電池壽命估算上要優于傳統的估算模型，證明了本文所提出的思想和方法具有一定的正確性和實用性。

2 蓄電池壽命預測模型

2.1 影響蓄電池壽命因素

蓄電池的壽命一般用SOH（State of Health）來反映，表示蓄電池在滿電條件下所能提供的有效電量，以當前實際容量占原來額定容量的比例來計算［6～9］。

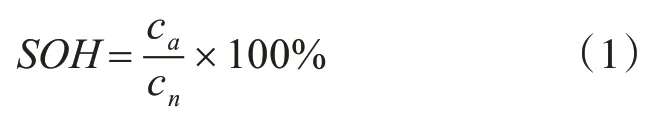
其中，ca為蓄電池滿電狀態下的實際容量，cn為蓄電池額定容量。當SOH 低于80%時，一般可認定蓄電池壽命到期EOL（End of Life）。

可見，蓄電池實際容量的估算是準確衡量蓄電池壽命的前提條件。蓄電池實際容量主要由兩方面因素決定，一是蓄電池在制造過程中由于工藝誤差造成的不可恢復影響因素，如電解液濃度的差別、極板幾何尺寸的大小等，這些因素會導致不同廠家、不同種類蓄電池的出廠實際容量與標定的額定容量之間有細微不同。二是蓄電池在使用過程中，由于內部發生劇烈電化學反應所引起的實際容量下降，如環境因素（溫度、氣壓）、放電電壓、放電溫度、循環次數等，這些因素是評估蓄電池壽命的主要參考因素［10～11］。

1）充放電時的溫度

蓄電池內部是一個動態平衡的電化學體系，溫度升高會加快電解液的電化學反應速率，從而釋放出更多電量；而溫度降低則會減緩電解液的電化學反應速率，從而釋放出更少電量。

2）工作電壓

在蓄電池充放電過程中，電壓與電量是個動態變化的關系。當放電電壓過低仍然持續放電時，則會造成極板上累積的化學物質難以復原；當充電電壓過高仍然持續充電時，則會由于大量氧氣的生成造成蓄電池鼓脹，同時伴隨著熱量的積累，最終對蓄電池的壽命造成損傷。

3）充放電倍率

放電電流越大，電池內部的化學反應速度會越快，在蓄電池正極板或負極板表面形成的硫酸鉛就越多，從而導致電池活性物質的反應速度下降，使得蓄電池所能提供的總電量變少。與此同時，硫酸鉛的不斷累積造成蓄電池硫酸鹽化，會進一步阻礙活性物質的化學反應，影響了蓄電池的放電能力。

4）蓄電池的不均衡性

由于蓄電池制造過程中在裝配工藝、使用材料等方面存在著微小的差異，從而使得每節電池其相關性能特性不一定一致。因此，在同一工作電流或生產環境下，蓄電池組的不同單節電池也會出現充放電容量等性能特性的不一致，所以蓄電池實際容量往往是由最小的單體電池實際容量來決定的。

5）循環壽命

在持續不斷的蓄電池循環充放電過程中，隨著循環過程的增多，蓄電池自身的活性物質機能會逐漸老化，進而使得蓄電池的電化學反應效能不斷降低，最終導致蓄電池完全喪失利用價值。

2.2 蓄電池壽命因子

蓄電池的壽命受眾多因素影響，是一個動態變化的過程。本文通過測定當前充電階段的蓄電池壽命狀態，以此作為計算蓄電池實際容量的修正因子，進而提高蓄電池實際容量的估算精度。

蓄電池壽命因子取當前可用容量占整個額定容量之比，以及循環使用次數占整個生命周期最大循環使用次數之比的兩者平均值作為因子數。同時考慮到蓄電池組內部不同單體蓄電池之間的不均衡性，其蓄電池組的性能根據“木桶原理”受限于最差的那塊單體蓄電池，可用蓄電池組最小電壓與平均電壓的比值進行修正。因此，蓄電池壽命因子如式（2）所示。

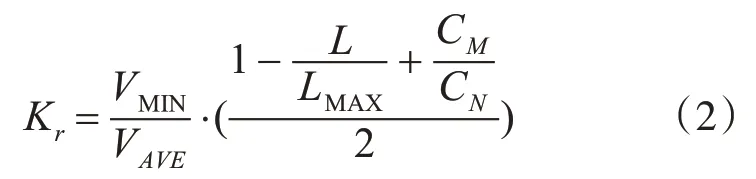
其中，VAVE表示蓄電池組的平均電壓，VMIN表示蓄電池組的最小電壓，LMAX表示廠家提供的最大循環使用次數，L 表示蓄電池當前的循環使用次數，CN表示廠家提供的額定容量，CMC 表示蓄電池當前的容量預測值。

2.3 改進的蓄電池壽命估算模型

傳統的蓄電池實際容量通常以電壓、電流和溫度等一直可直接測量的特性值來估算，但未考慮到蓄電池使用過程中的老化情況，因此對蓄電池實際容量的估算精度并不太高［12～13］。

本文在綜合電壓、電流和溫度測量值作為輸入以外，將壽命因子也引入到模型中，提高動態條件下的估算精度，其改進的蓄電池壽命估算模型為

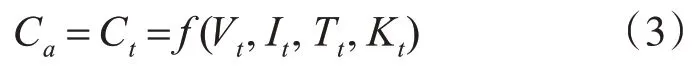
3 神經網絡的訓練

3.1 基于LM的BP神經網絡

BP（Back Propagation）神經網絡具有不依賴某個具體對象模型，只需在確定網絡結構與樣本集后即可實現輸入/輸出非線性映射的優點［14～15］。其輸出誤差為

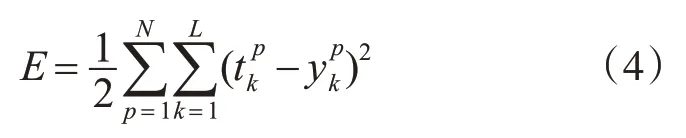
其中，N 為模式樣本對，L 為網絡輸出節點數，分別為在樣本p 作用下，輸出節點k 期望輸出與實際輸出。

BP 神經網絡只有通過不斷訓練才能實際應用到蓄電池壽命的測試，由于BP 神經網絡的收斂速度和運算時間等性能參數受到訓練算法的不同會有著不同的影響。為綜合比較不同訓練算法對BP神經網絡的影響程度，本文采用常用的三種訓練算法對網絡進行訓練，并觀察結果。從表1 可見，三種訓練算法中LM 法的收斂速度最快，輸出方差最小。這也是LM 法的優勢所在。本文將選用LM 法作為BP 神經網絡訓練的依據。

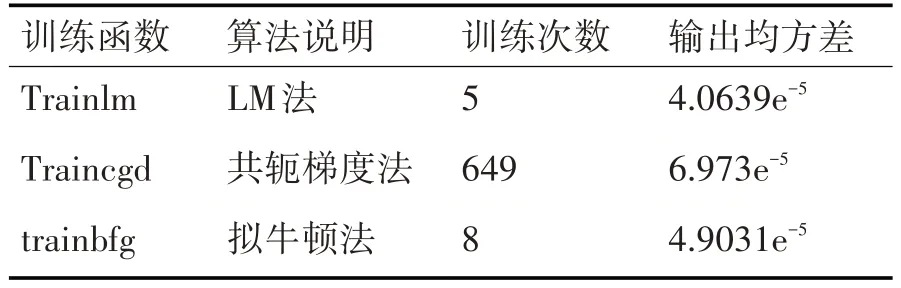
表1 BP神經網絡三種訓練算法性能對比表

3.2 改進的LM-BP神經網絡

多層LM-BP 神經網絡理論上可實現任意的線性和非線性函數的映射。但在實際應用中，LM-BP神經網絡在訓練過程中容易陷入誤差性能函數的局部極小值，從而導致網絡訓練失敗。因此，本文引入 GAAA（Genetic-Algorithm Ant-Algorithm）算法，利用遺傳算法和蟻群算法優化LM-BP 神經網絡的權值和閾值。其核心思想是蟻群算法中的初始信息素借助遺傳算法所具有的隨機性、快速性以及全局收斂等優點進行結果計算；根據蟻群算法所具有的全局優化、正反饋特性、并行計算以及全局收斂的優點，進行具體設計。其主要算法流程如圖1所示。

1）適應度函數計算：選擇BP 神經網絡訓練得到誤差的平方和求倒數作為適應度函數。

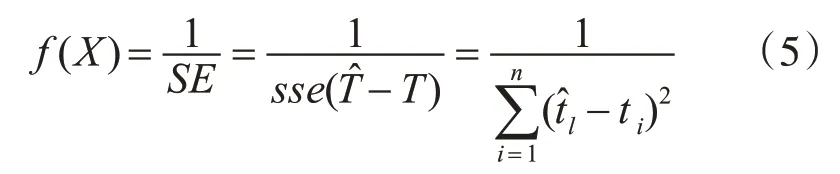
2）初始種群的生成：在對樣本數據進行預處理后，隨機生成初始種群。

3）選擇算子操作：本文采用最常用的比例選擇算子，它選擇個體是依據個體適應度值的概率來進行的，其表達式如下：

式（6）中，Fi為個體i 的適應度，M 為群體大小，pi表示個體i被選中的概率。

4）交叉、變異操作：交叉操作選用單點交叉算子，可在解空間中進行有效搜索，同時又能對有效模式造成相對較小的破壞；變異操作則可采用基本位變異算子。

5）初始化信息素參數：根據優化解生成信息素初始分布，在將n個節點上放置m只螞蟻。

式（7）中，τS為信息素初值，τC為蟻群算法中設定的信息素常量，τG為遺傳算法中求解結果轉換得到的信息素值。

6）更新所有路徑信息素表：

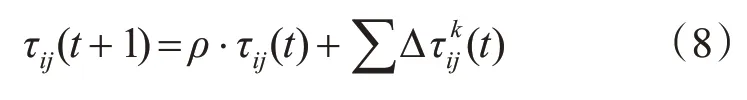
式（8）中，τij(t)為路徑（i，j）在t 時刻軌跡上的信息素強度，ρ(0 ≤ρ＜1)為軌跡的持久性，為螞蟻k在路徑（i，j）中單位長度中的軌跡信息素。

4 算例分析

針對BP神經網絡中自身的固有缺陷所導致的訓練不精確性，本文提出將BP 神經網絡算法與GA-AA 算法綜合的改進BP 神經網絡算法，利用傳統BP 神經網絡算法與改進的BP 神經網絡算法分別對蓄電池壽命系統模型估算實驗。其中在壽命系數模型中輸入變量有四個，分別為電流、電壓、溫度和壽命因子，輸出變量為蓄電池的實際容量值，設定神經網絡的最大誤差指標goal=10-5，訓練的最大迭代次數epoches=1000，計算最大目標值goal 的尋優過程，通過對傳統BP 神經網絡算法與改進的BP 神經網絡算法的訓練及樣本測試，得到蓄電池實際容量在仿真驗證環境中的預測輸出效果，如圖2所示。

圖1 改進的LM-BP神經網絡算法流程圖

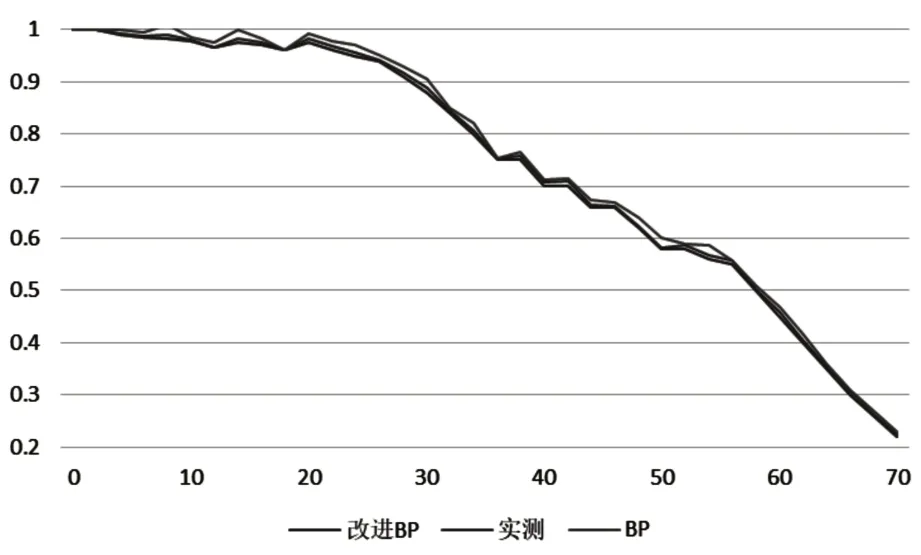
圖2 兩種網絡對蓄電池實際容量的預測輸出圖

兩種神經網絡對蓄電池實際容量的估算誤差如圖3所示。

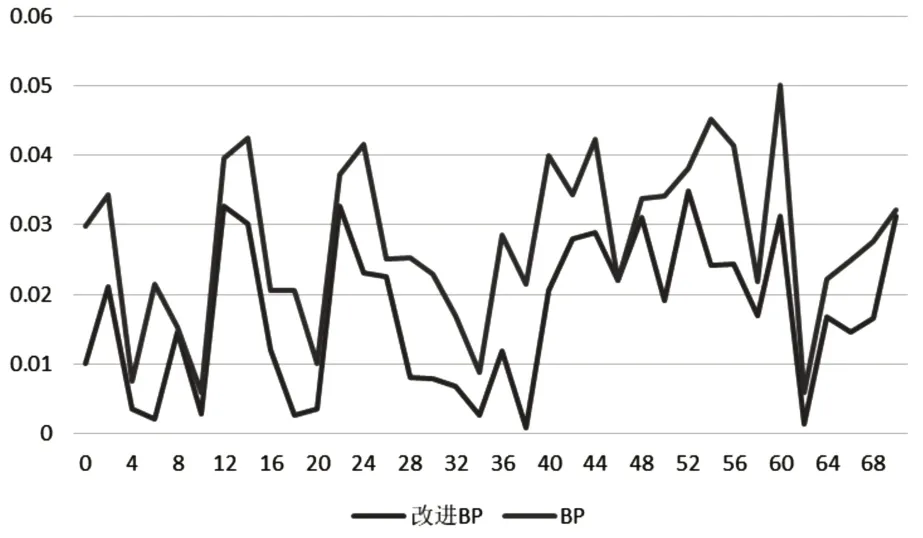
圖3 兩種網絡估計輸出和實測值的相對誤差

可見，兩種神經網絡算法對蓄電池實際容量的估算誤差均在國家規定的8%估算誤差范圍內，但改進的BP神經網絡算法的誤差偏離度優于傳統的BP 神經網絡算法，對蓄電池實際容量的估算具有顯著進步的估計效果。

5 結語

本文以變電站中的蓄電池為研究對象，針對使用過程中蓄電池老化以及當前健康狀態變化所導致的蓄電池壽命變化，引入了一種蓄電池壽命修正因子，構建了一種改進的蓄電池壽命估算模型。通過對神經網絡三種學習函數的性能比對，選用LM法作為BP 神經網絡的訓練算法。同時，針對傳統BP 神經網絡存在的局部極值缺陷，利用改進的BP神經網絡算法，提出了一種利用優化逆向傳播的神經網絡，同時為了修正網絡權值和閾值引入了遺傳和蟻群算法。設計神經網絡的輸入分別為電流、電壓、溫度以及壽命系數，通過BP 神經網絡和改進BP 神經網絡算法的仿真驗證，結果表明改進的BP神經網絡算法對蓄電池實際容量估算的精度較高，具有較強的實用性。

由于實驗時間、試驗環境、樣本數量等因素的制約，現有工作還有不少進一步改良空間。不同蓄電池類型之間的工作原理及特性存在著較大的差異，后續可考慮將蓄電池類型作為神經網絡算法的輸入數據之一，利用不同類型電池的兼容性觀測或修正估計算法，以提高本方法的通用性。