復數階累加的灰色系統模型

吳正鵬，陳見柯，柴劍平

(中國傳媒大學數據科學與智能媒體學院，北京 100024)

1 介紹

自古以來，人們就關注著基于現有記錄的對即將到來事情的預測。隨著科學技術的發展，人們現在生活在一個“大數據”時代。盡管如此，馬鑫最近發布的一篇論文聲稱，基于小樣本的高效學習仍有可能訓練智能AI，大數據不應該是高效AI 的唯一途徑[12]。此外，由于這些高速的發展，自然會出現新的現象和問題(例如，二氧化碳排放標準、網絡突發輿論、能源消耗等)，應該有快速且高效的應急設施。就像可怕的自然災害一樣，相關的靜態結果可能是不完整的，或者是不充分的。因此，關于小信息量的預測問題仍然存在很多情況。

20 世紀80 年代，鄧聚龍提出了灰色系統理論[3,4]，為解決信息貧乏情況下的小樣本預測問題提供了一種新的方法。GM(1,1)模型，即一元一階灰色模型，在整個理論中起著至關重要的作用。鄧還給出了原始GM(1,1)模型的幾種不同形式。此后，許多學者繼續為這一理論發展不同的模型[9,10]。到目前為止，在理論修改（例如，尋找更好的模擬和預測結果[25]）和優化算法（灰狼優化、粒子群優化[13]）方面，朝著這個方向取得了許多進展。對原始GM(1,1)模型進行了不同形式的修正，以適應不同的預測情況，例如抗拉強度[16]、二氧化碳排放[21]、冰塞災害[11]等的間接度量。對于給定的時間序列，為了在未來的預測中引入定性分析（即強度或弱化Γ，劉思峰提出了（包括加強和弱化）緩沖算子的思想[10]。這些算子滿足3個公理：不動點、充分利用信息、解析性和正規性。許多學者開發了這類工具，將緩沖運算符應用于不同類型的模型預測[24]。

萊布尼茨提出的分數階微積分思想對灰色系統也有很大的影響。吳立峰、劉思峰等人[23]首次考慮了分數階累加的灰色模型。該公式將整數階累加的經典灰色模型推廣到分數階灰色模型。這一創新在理論和實踐上都對灰色系統進行了巨大的改進。從那時起，分數階累加成為灰色系統中一種流行而有效的工具[14,22]。為了在舊信息和新信息之間保持平衡，李沖、英杰、昂英杰等人提出了自己的觀點，開發了新的序列運算符[8]。

目前，Matlab 軟件已取代Visual C#，成為大多數研究灰色系統的學者的主要計算機編程工具，他們大量使用Matlab 語言中嵌入的伽馬函數。但Matlab 語言中插入的伽馬函數不能直接編譯出一般的復數值（例如Γ(1+i)）。本文利用冪零矩陣和泰勒級數，給出了復數累加的灰色模型的一種新的、直接的表述。由于復數域X 是代數閉域，也是拓撲完全域[7]，這個公式將經典的整數累加的灰色模型[3]和分數累加的灰色模型[23]推廣到其最一般的形式。正如我們將看到的，復雜積累的灰色模型將會得到更好的模擬結果和預測結果。

本文組織如下。第二節討論了經典的整數（分數）階累加生成算子和一階一元GM(1,1)微分方程的灰色模型。我們將分數累加生成運算符(因此，自動包含整數的情況)推廣到復數累加生成運算符。考慮所有復數累加生成算子的集合，我們將證明該集合具有一維復李群結構。在第三節中，我們建立了復數累加的灰色模型（對于某些z∈X，用CAGMz(1,1)表示），并確定了它的解。由于我們可以將實數P 看作X 的一維子空間，即我們在一個更大的區域上工作，自然會期望CAGMz(1,1)模型產生比類似模型更低的平均絕對百分比誤差MAPE 和均方根百分比誤差RMSPE（其定義將在稍后給出）。在第四節中，通過幾個具體的例子討論了CAGMz(1,1)模型相對于類似模型的優勢。第五節介紹了對本研究的一些期望。

2 復數累加生成算子

設X(0)= (x(0)1,x(0)2,…x(0)n)是原始數據序列。對于1≤k≤n，設x(0)k∈X為時間k時的值，數據序列是列序列還是行序列，只是轉置不同而已。為方便起見，我們將在以下結構中使用行序列。設n=dim(X)是行數據序列空間的維數。對于實際問題和具體問題，應該注意到數據序列中的條目是鐵的生產量、用電量、某一地區的GDP、二氧化碳排放量等，所以一般地這些x(0)i∈Θ。但我們想以最一般的形式來構建這個行動。

2.1 傳統累加生成算子與GM(1,1)模型

一階累加生成算子和一階逆累加生成算子在灰色系統理論中占有重要地位。基于這些運算，GM(1,1)模型是灰色系統理論中的一個基本模型[9,10]。

定義1設X(0)= (x(0)1,x(0)2,…x(0)n)是原始數據序列。設X(1)= (x(1)1,x(1)2,…x(1)n)是數據序列，如果我們對X(0)應用一階累加生成算子，X(0)的坐標由下式給出

X(0)的一階逆累加生成算子表示為X(-1)，其坐標由下式給出

很容易驗證一階累加生成算子和一階逆累加生成算子是對數據序列的逆運算。

對于2 ≤k≤n，設w(1)k=。那么方程

稱為GM(1,1)模型的原始形式。a,b為GM(1,1)模型的參數。a,b的最小二乘估計由下式給出

其中

在初始值x(1)1=x(0)1的情況下，白化方程

的時間響應序列由下式給出

其中1≤k≤n。最后，如果對序列(x(1)1,x(1)2,…x(1)n)應用一階逆累加生成算子，則模擬序列滿足

其中2≤k≤n.

2.2 復數累加生成算子

定義2[23]設原非負序列X(0)的r(r∈P>0) 階累加生成算子為X(r)。然后

與傳統的整數階累加灰色模型相比，分數階累加灰色模型在實際應用中（無論是理論基礎還是模型仿真）都會得到更好的結果。分數階灰色模型在許多不同的場合得到了廣泛的應用。許多學者提出了建立這一理論的新方法[13,14,15]。

為了將現有的理論推廣到復累加生成算子的情形，我們將使用代數公式[6,7]。

設x是冪零不定式，使得xn= 0，則顯然

分別設f(x) =(1+x+x2+ …+xn-1)和g(x) =(1-x).設

即I是n×n單位矩陣，E1是冪零矩陣。對于1≤k≤n，設Ek:=Ek1.直接計算如下

En=En1=On×n，其中On×n為零矩陣。然后，對于一階累加生成算子A和一階逆累加生成算子A-1，存在

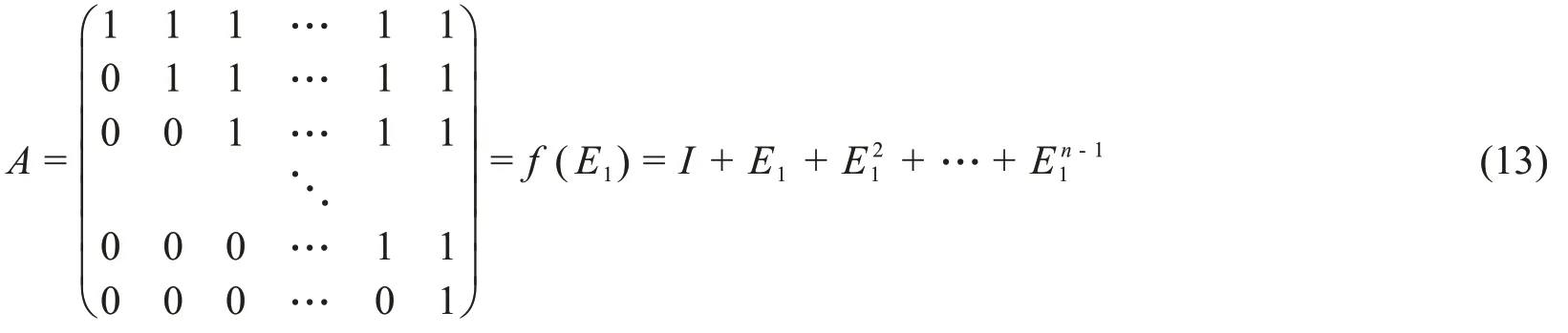
或者等價地f(E1)g(E1)=I。歸納地，第二累加生成算子A2等價于f2(E1)。通過為z∈X設置A(z):=f z(E1)，我們將給出以下定義：

定義3設X(0)為原始數據序列并且z∈X，則第z次復數累加生成算子由A(z)定義。如果我們用X(z)表示第z個累加數據序列，那么

其中符號· 表示通常意義上的矩陣乘法。

定理1所有z∈X 的第z個累加生成算子集構成一個1維交換加性李群，它與X同構。

3 復累加的灰色模型

設X(0)=是原始數據序列，z∈X使得Im(z) ≠0 是復數。如上所述，對于1≤k≤n，一般地∈P。設是第z個復數累加生成序列。在第z次復數累加生成運算 之 后，對 于 1≤k≤n，有∈X。 設W(0)=(w(0)2,…,w(0)n)是X(z)的連續鄰域序列的平均生成，即對于2≤k≤n，w(z)k=.我們給出以下定義：

定義3 對于2≤k≤n，方程式

將被稱為第z個復數累加生成運算的灰色模型的原始形式，其將被表示為CAGMz(1,1)。常數a稱為灰色發展系數，b稱為灰色控制參數。

注1如果z= 1，這是經典的GM(1,1)模型。對于復累加情況的灰色系統模型，應該注意到這兩個參數，即a和b，一般都是復數。

CAGMz(1,1)模型的普通最小二乘估計序列滿足

其中

定義4設B,Y,a,b如上所述，微分方程

將稱為CAGMz(1,1)模型的白化方程。

在初始值x(z)1=x(0)1的情況下，很容易得出時間響應序列具有以下形式

對 于 2≤k≤n.最后，如果我們對序列應用第(-z)次復數累加生成A(-z)(或者等價地，第z次復數累加生成操作的逆運算)，我們將得到模擬序列，即

設X(0)=是原始數據序列，我們可以假設x(0)k=αk+iβk，其中αk,βk∈P.將CAGMz(1,1)模型應用于X(0)，并設為仿真數據序列(0)=。一般地，由于(0)k∈X，我們可以假設?，其中，設ε=(ε1,ε2,…,εn)是剩余序列，則

為了對CAGMz(1,1)進行誤差分析，同時對已有的理論進行推廣，我們將利用復數的模來對其進行誤差分析。更準確地說，設Δ =(Δ1,Δ2,…,Δn)為相對誤差序列，則

綜上所述，給定一個原始數據序列X(0)=(x(0)1,x(0)2,…x(0)n)，建立第z個CAGMz(1,1)模型的步驟如下：

步驟1：選擇復數z∈X，使得Im(z) ≠0，并計算第z個累加生成數據序列，即X(z)=X(0)·A(z)；

步驟2：計算X(z)的連續鄰域序列W(z)的平均生成量；

步驟3：通過對復矩陣的最小二乘估計，給出了參數a,b的估計，即=(BHB)-1BHY，其中B,Y由方程(x(z)k-x(z)k-1)+aw(z)k=b給出，BH為B的復共軛轉置矩陣；

步驟5：通過經由A(-z)將第(-z)復數累加生成運算(第z個累加生成運算的逆運算)應用于(z)來計算模擬值(0)，即(0):=(z)·A(-z)；

步驟6：計算殘差數據序列ε 和相對誤差數據序列Δ，進行誤差分析。

對于具體問題，通過選擇一個有理數作為累加生成順序，即z∈Θ，則A(z)中累加生成算子的條目和模擬值(0)都是有理數，即A(z)i,j∈Θ，1≤i,j≤n和，1≤k≤n。由于大多數預測模型的模擬值仍為正有理數，即取模數與模擬值相同，即，1≤k≤n。由于累加生成階數可以從所有復數中選擇，因此可以認為CAGM模型是分數累加灰色預測模型的推廣。

4 個案研究

案例1

我們考慮的第一個例子是瀝青混合料，它廣泛應用于道路建設中。在一定的條件下(例如，激振頻率、材料溫度等)，瀝青混合料的變形緩慢(粘性)，一旦變形力消失(彈性)，瀝青及其混合料的這種性質稱為粘彈性。瀝青混合料的復模量E*(=E′+iE″，一個復數)由兩部分組成，其中E′表示混合料的儲能能力(彈性行為)，E″表示耗能能力(粘性行為)。動態模量E*被定義為模量[27]。

早期對E*的研究主要集中在動態模量主曲線[19]，忽略了E*的θ相位角，而后者也是瀝青和瀝青混合料的一個重要影響因素，例如，最近的一項研究發現，相位角是區分瀝青混合料噪聲特性的一個很好的實驗室參數[1]。近年來，研究人員試圖開發相角的主曲線[2,26]，曾鳴等人提出的廣義CAM 模型由復模量主曲線、相角主曲線[28]組成。Venudharan 等人發展了儲能模量和損耗模量的預測模型[17]。可以同時考慮動模量E*和相位角θ。表1和表2列出了AC-20C 70#型瀝青混合料的實驗值[2]。

表1 AC-20C 70#瀝青混合料的動模量(MPa)

表2 AC-20C 70#瀝青混合料的相角(°)

通過歐拉公式eiθ= cosθ+isinθ，任意復數z=a+bi可以重寫為z=|z|·eiθ，其中是模數，θ是相位角(tanθ=，a≠0)。以溫度4.4°C 為例，原始復數數據序列(取決于頻率)為

作為比較，我們選擇3 個累積生成階z= 0.9 + 0.12i，z= 1 和z= 0.5 來構建CAGMz(1,1)模型。第0.9 +0.12i個累加生成算子A(0.9 + 0.12i)為

z= 1和z= 0.5的累積生成算子與一階和分數階的累積生成算子相同。

應用這些運算符，我們將得到第0.9+0.12i個累加生成數據序列

一階累加生成數據序列為

0.5階累加生成數據序列為

當z= 0.9 + 0.12i時，a= 0.074 - 0.025i，b= 14211.04 + 4390.87i，時間響應方程(對于k= 2,3,…,6)

當z= 1時，a= -0.098+ 0.007i，b= 15558.57+3579.62i，時間響應方程(對于k= 2,3,…,6)

當z= 0.5時，a= 0.043- 0.0087i，b= 11072.99+2088.93i，時間響應方程(對于k= 2,3,…,6)

由于原始數據序列X0和模擬數據序列0都是復數，為了進行誤差分析，我們將使用復數的模來進行誤差分析。以第(0.9 + 0.12i)次復數累加的相對誤差Δ6為例，

表3列出了復模量數據序列CAGMz(1,1)模型的三種不同的模擬值和誤差。

表3 CAGMz(1,1)模型的模擬值和誤差

案例2

下面的例子描述了1994-2000年間美國的旅游需求[18,22]。基于這些實際值建立了四個不同的灰色模型(我們考慮了CAGMz(1,1)模型的三個不同參數)，并以來年(2001年，樣本外)為預測對象。所有結果都列在表4中。

如上所述，承認了關于預測的MAPE 建模的MAPE。為了使預測MAPE 取一個較低的值，可以取z1= 1.232 - 0.506i，CAGMz1(1,1) 模 型 給 出 的 預 測MAPE最低(≈0.00116%)。對于這種情況，雖然模型的MAPE 高于其他三種模型，但這兩種MAPE 的總和仍然很低(≈3.13%，而GM1.2(1,1)模型為3.7%)。設置z2=1.176-0.13i，則建模的MAPE 為1.33%，這是表4所列結果中的最低值。出于另一個考慮，我們可以選擇z3= 1.23- 0.5i，這仍然是一個更好的模擬。

表4 四種不同模型的擬合值和MAPE

5 結論

本文將整數、分數累加生成算子推廣到復數累加生成算子。結合所有的復數累加生成算子，我們得到了一個自然的一維可加復李群結構，它與X同構。與以前關于實數(整數或有理數)的討論相比，我們的工作是在整個復平面上進行的。復數階累加生成算子可以同時調整新舊信息之間、實部和虛部之間的權重，可以得到更好的仿真和預測結果。通過幾個實例，討論了復數累加灰色模型與常用方法相比的優越性。

為了進一步研究，我們將列出幾個可能的問題：

(1) 灰色理論中的一些技術，例如光滑比ρ、區間灰數、灰色關聯算子等都依賴于P中的階關系，但復數域X不存在階關系。如何將這種技術擴展到復數數據序列的情況；

(2) 將分數階微積分的思想引入灰色理論，提出了分數階累加生成算子。根據我們的構造，將累加生成階推廣到復數，人們可能會問：是否存在復數階演算？

(3) 尋找涉及復雜數據序列的復雜灰色模型的應用，例如復信號分析、瀝青及其混合料的粘彈性等。