行波效應對公軌兩用獨塔單索面鋼桁梁斜拉橋地震反應影響分析

曾 勇 曾渝茼 譚宇杰 邱 周 余 浩

（1.重慶交通大學山區橋梁及隧道工程國家重點實驗室，重慶 400074；2.重慶交通大學山區橋梁結構與材料教育部工程研究中心，重慶 400074）

0 引 言

長江流域的重慶、武漢等城市，修建了各種各樣的大跨度橋梁，特別是城市軌道交通技術逐漸發達的今天，公軌兩用橋成為熱門。公軌兩用橋通常需要將橋面做成雙層，一層供汽車行駛，另一層則是軌道交通。鋼桁架主梁是最適合做雙層橋面的形式之一，獨塔單索面鋼桁架斜拉橋因其跨度大、功能全面、結構新穎備受關注。特大橋必須進行抗震設計［1］，強地震作用可能會對大跨度獨塔單索面鋼桁架斜拉橋造成十分復雜的破壞，因此對其抗震性能的研究具有重大意義。

行波效應是地震動三種空間變化特性之一，不能忽視行波效應對特大橋地震的影響。閆聚考等［2］對多塔懸索橋進行了全橋振動臺試驗，發現行波效應對橋梁的影響與地震波的特性密切相關；王再榮等［3］對超大跨斜拉橋進行了有限元結構分析，發現行波效應會增加橋梁的地震損傷；王浩等［4］研究了行波效應對大跨鋼管混凝土拱橋的影響，也得出了行波效應的影響與地震波特性密切相關的結論；張亞輝等［5］通過研究發現地震響應隨視波速的變化有較為明顯的變化，忽略行波效應的影響對于結構設計是偏于危險的；文獻［6-9］研究了連續剛構橋地震行波效應，結果顯示視波速對大跨度連續剛構橋的影響仍然不可忽略；宋波等［10］發現視波速對鋼拱橋的地震反應影響較大，不可忽略；焦常科等［11］發現橋梁地震分析中，應適當選取地震波和視波速；陳清軍等［12］的研究表明考慮行波效應后，大跨斜拉橋地震作用下的位移和彎矩有所減小。可見，行波效應對于橋梁地震有極其復雜的影響，對于不同類型的橋梁，行波效應可以有利于橋梁地震反應也可對其不利，視波速對各種橋型的大跨徑橋梁的地震響應的影響均不容忽視。

以往的研究主要集中于對其他橋型或公路斜拉橋的行波效應研究，對于公軌兩用獨塔單索面鋼桁架斜拉橋地震行波效應的研究甚少，研究獨塔單索面鋼桁架斜拉橋地震行波效應對于評價其抗震性能極其重要。本文選取了3種具有不同頻譜特性的地震波，采用橋梁有限元結構分析軟件MIDAS，從地震作用下索塔最大彎矩和位移以及鋼桁架主梁的最大軸力和位移兩個方面研究了行波效應對某獨塔單索面鋼桁架斜拉橋的影響。公軌兩用獨塔單索面鋼桁架斜拉橋造型新穎、結構復雜［13-14］，研究其行波效應的影響具有重大實際意義且可以為相似工程的抗震設計提供參考。

1 工程概況和有限元模型

1.1 工程概況

某獨塔單索面鋼桁架斜拉橋如圖1所示，跨徑設置為（88+312+240+80）m，橋梁全長720 m。鋼桁架主梁雙層布置，上層供汽車行駛，下層雙向輕軌，主桁桿件為焊接箱型截面，采用整體節點，雙層橋面采用正交異性橋面板。橋塔是融合了中華元素的“天梭”造型，塔高182 m。斜拉索采用稀索單索面設計，可能會增大地震作用對橋梁的影響。地區基本地震烈度為VI度，橋梁地震設防烈度為VII度。

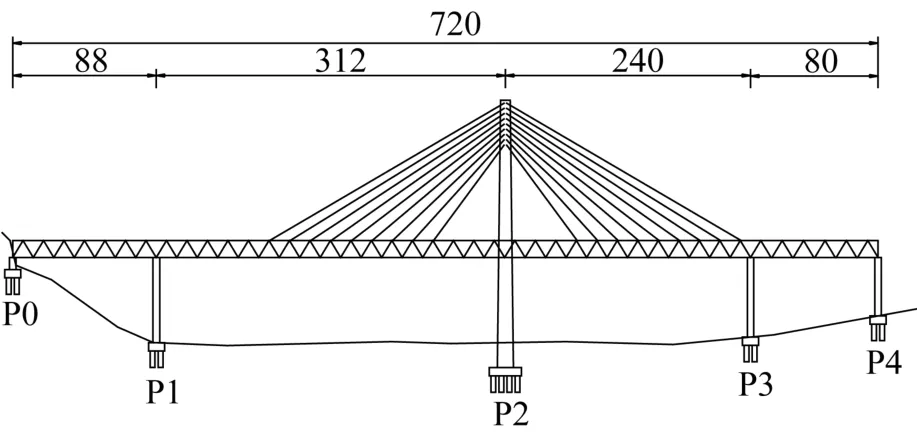
圖1 某獨塔單索面鋼桁架斜拉橋（單位：m）Fig.1 A steel truss cable-stayed bridge with single tower and single cable plane（Unit：m）

圖2 索塔效果圖Fig.2 Effect drawing of cable tower

1.2 有限元模型

采用MIDAS構建橋梁有限元模型如圖3所示，共設置12 288個節點、24 515個單元，單元數目合適且達到了足夠的精度，對于橋梁各個構件的模擬準確，橋梁主要部件單元類型和材料見表1。根據橋梁的實際情況，設置支承邊界條件。P1墩、P2墩、P3墩支承是指墩底的支承，P0墩和P4墩由于并未在模型中實際建模，因此指墩頂的支承。P1墩、P2墩、P3墩墩頂先共節點與上部結構連接，后釋放梁端約束以模擬支座，P2墩墩頂設置固定鉸支座，P1墩和P3墩墩頂設置縱向活動鉸支座。輸入3種不同的地震波，并且將每個地震波的視波速設置為300 m/s到7 000 m/s之間，采用非一致地震動分析法探究行波效應對獨塔單索面鋼桁架斜拉橋地震反應的影響。

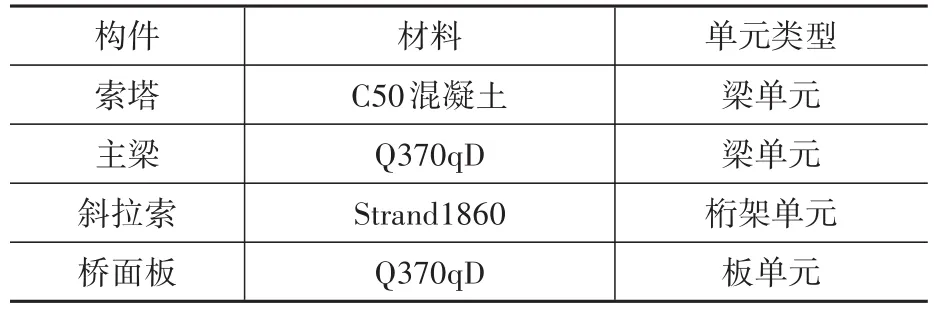
表1 主要部件單元類型和材料Table 1 Main component unit type and material

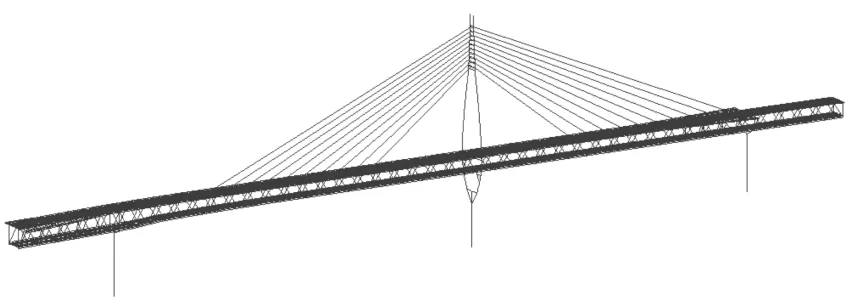
圖3 有限元模型圖Fig.3 Layout of finite element model

2 地震動輸入

2.1 地震波的選取

選取3種PGA（加速度峰值）、頻譜特性和地震持續時間均完全不同的地震波，以探究不同種地震波下，行波效應對大跨度獨塔鋼桁架單索面斜拉橋的影響。三種地震波分別為：1979 James RD El Centro 220 Deg地震波（加速度峰值0.367 3g，持續時間37.68 s）、1994 Northridge Sylmar County Hosp 90 Deg（加速度峰值0.604 7g，持續時間59.98 s）和人工波（加速度峰值0.104 3g，持續時間24.96 s）。橋梁的設防烈度為VI度，將PGA進行調整，使其符合場地特征，調整后的結果也更具科學性和針對性。地震動輸入的方向為順橋向，因為行波效應在跨度較大的順橋向才會明顯，橫、豎向地震由于跨度較小對于行波效應的影響微乎其微。

2.2 PGA調整系數的確定

本橋主跨跨徑312 m，屬特大橋，橋梁抗震設防類別為A類；橋梁設防烈度為VI度，橋梁抗震設防措施等級VII度。最大值水平加速度反應譜計算公式為

式中：Ci表示橋梁重要性系數，E2地震作用下的A類橋梁取1.7；Cs表示場地系數，場地類型為II，抗震設防為6的橋梁取1.0；Cd表示阻尼調整系數，通常情況下取1.0；A表示水平向基本地震動加速度峰值，抗震設防烈度為VI度的橋梁，取0.05g。

設計加速度最大值PGA的計算公式如下：

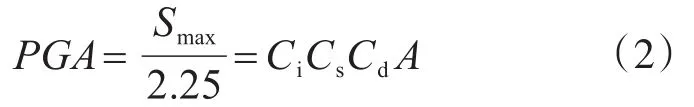
加速度峰值PGA調整系數計算公式為

式中：Pk為所選取的地震波加速度反應譜峰值。

聯合式（2）和式（3），加速度峰值PGA調整系數就可以被表示為

2.3 調整后的3種地震波

通過式（4），分別計算 1979 James RD El Centro 220 Deg地震波、1994 Northridge Sylmar County Hosp 90 Deg地震波和人工波在E2地震作用下的PGA調整系數，結果如表2所示，調整過后的三種地震波如圖4所示。

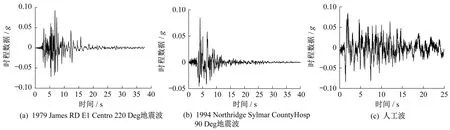
圖4 調整過后的3種地震波的時程函數Fig.4 Three kinds of time history function of seismic wave after adjustment

表2 各地震波在E2地震作用下的PGA調整系數Table 2 PGAadjustment coefficient of each seismic wave under E2 earthquake

3 行波效應地震分析

選擇計算精度可靠的非一致地震動分析法實現行波效應的模擬，選取三種PGA、頻譜特性和地震動持續時間均完全不同的地震波，目前記錄到的地震波的視波速主要集中在300～7 000 m/s，因此每種地震波的視波速都設置在此區間，探究行波效應對獨塔單索面鋼桁架斜拉橋的索塔以及鋼桁架主梁影響。圖5和圖6中，從左到右分別表示為1979 James RD El Centro 220 Deg地震波、1994 Northridge Sylmar County Hosp 90 Deg地震波、人工波下的響應情況。

3.1 索塔地震響應分析

在地震作用下，索塔會發生變形，各截面也會產生內力。三種地震波作用下，每種地震波的視波速設置為300～7 000 m/s，索塔的最大位移值和最大彎矩值沿塔高分布如圖5所示（圖5中塔座坐標為0 m，上塔頂坐標為182 m，塔高共182 m）。

圖5 三種地震波不同視波速下索塔最大位移和最大彎矩沿塔高分布圖Fig.5 Distribution of maximum displacement and bending moment with height of cable tower under three different apparent wave velocities

分析圖5（a）可知：

（1）三種地震波不同視波速下地震作用下索塔最大位移沿塔高分布的變化規律不完全一致。最左為1979 James RD El Centro 220 Deg地震波作用下的響應圖，各視波速下最大位移隨塔高變化的規律一致，先增加后下降，最后再增加；中間為1994 Northridge Sylmar County Hosp 90 Deg地震波作用下的響應圖，各視波速下最大位移隨塔高先輕微增加后猛增；右邊為人工波作用下的響應圖，各視波速下最大位移隨塔高先增加后趨于常數。選取的三種地震波雖然已將加速度峰值調為0.085g，但由于其頻譜特性不同，因此三種地震波不同視波速下地震作用下索塔最大位移沿塔高分布的變化規律不完全一致。

（2）在 1994 Northridge Sylmar County Hosp 90 Deg地震波和人工波作用下，視波速到達某一值后隨視波速的增加，各視波速下索塔最大位移隨塔高分布曲線較為集中，但1979 James RD El Centro 220 Deg地震波作用下卻沒有這個規律，這是因為選取的三種地震波具有不同頻譜特性和地震動持續時間，且索塔的位移是較為敏感的參數。在1994 Northridge Sylmar County Hosp 90 Deg地震波作用下的響應圖中視波速由300～500 m/s變化很大，這是因為視波速在300～500 m/s范圍內屬于低波速，而橋梁結構總長為720 m，對于低波速范圍內的波速變化較為敏感。在低波速范圍內，波速增加或減少100 m/s，相當于增加或減少了0.36 s以上橋梁結構感知地震波的時間，而100 m/s的變化在5 000 m/s以上高波速下，橋梁感知地震波時間變化還不到0.003 s。

分析圖5（b）可知：

（1）三種地震波不同視波速下索塔最大彎矩隨塔高分布相似，均為先猛降后緩降，最后變得很小，但地震作用下索塔高度對應的最大彎矩值不同，人工波作用下的各個塔高對應的彎矩值均較大，說明在不同頻譜特性和地震動持續時間的地震波作用下，索塔的最大彎矩變化規律仍然相似，地震作用下索塔的最大彎矩變化規律受不同頻譜特性和地震動持續時間影響較小，但地震作用下最大彎矩值仍然受影響，人工波有效時間持續較長且在有效時間期間沒有發生明顯衰弱，因此在人工波作用下的索塔彎矩值整體最大。

（2）三種地震波作用下，當視波速大于300 m/s后，隨視波速的增加，各視波速下索塔最大彎矩隨塔高分布曲線較為集中，這說明地震作用下索塔最大彎矩在行波效應研究中為非敏感因素。當視波速較小時，地震波到達橋梁各墩的時間差較大，即使是非敏感因素在低波速下也會表現得不穩定，值得重視。

3.2 主梁地震響應分析

在地震作用下，鋼桁架主梁會發生變形，各截面也會產生內力。三種地震波作用下，每種地震波的視波速設置為300～7 000 m/s，隨橋梁長度變化，選取各長度下某一根桿件的進行研究，桿件的最大位移值和最大軸力值隨橋梁長度分布如圖6所示。

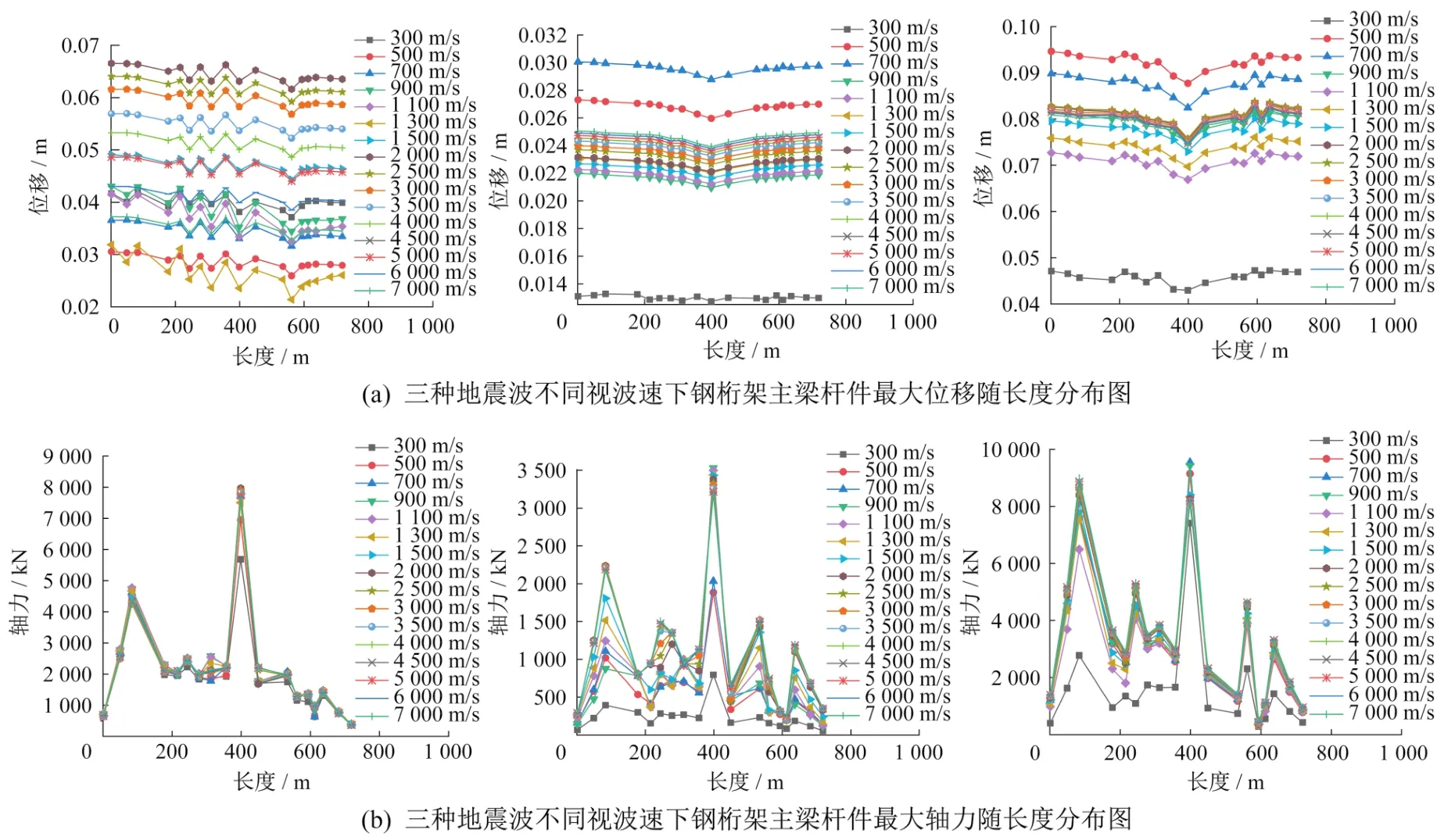
圖6 三種地震波不同視波速下鋼桁架主梁桿件最大位移和最大軸力隨長度分布圖Fig.6 Maximum displacement and axial force distribution with height of steel truss girder members under three different apparent wave velocities

分析圖6（a）可知：

（1）三種地震波不同視波速下鋼桁架主梁桿件最大位移隨長度分布規律不完全一致。最左為1979 James RD El Centro 220 Deg地震波作用下的響應圖，各視波速下最大位移隨橋梁長度分布不均勻；中間為1994 Northridge Sylmar County Hosp 90 Deg地震波作用下的響應圖，各視波速下最大位移隨橋梁長度先平緩下降后平緩增加，增、降幅均很小，整體曲線較為平緩；右邊為人工波作用下的響應圖，各視波速總體先緩慢下降，后緩慢上升，整體曲線比1979 James RD El Centro 220 Deg地震波作用下的曲線平緩但較1994 Northridge Sylmar County Hosp 90 Deg地震波作用下的曲線曲折。這是因為1979 James RD El Centro 220 Deg地震波在地震作用的2到16秒之間時，時程數據較為波動，且波動較大的持續時間較長達到14 s，因此地震響應曲線最為波動；1994 Northridge Sylmar County Hosp 90 Deg地震波在地震作用4～011 s時，時程數據有些許波動，但波動不劇烈且時間較短，因此地震響應曲線最為平緩；人工波1.5～24.5 s都在波動，波動時間較長達到23 s，但波動的較1979 James RD El Centro 220 Deg地震波平緩。

（2）與行波效應對索塔最大位移的影響相似，在1994 Northridge Sylmar County Hosp 90 Deg地震波和人工波作用下，視波速到達某一值后隨視波速的增加，各視波速下鋼桁架主梁桿件最大位移隨長度分布曲線較為集中，但1979 James RD El Centro 220 Deg地震波作用下卻沒有這個規律。

分析圖6（b）可知：

（1）三種地震波不同視波速下鋼桁架主梁桿件最大軸力隨長度分布規律總體相似，均為隨橋梁長度先增加到88 m然后減小，在88～360 m較為波動，從360 m猛增到400 m，400 m猛降到440 m，在440～720 m較為波動，但橋梁長度所對應的最大軸力的數值不同，說明地震作用下主梁最大軸力變化規律受頻譜特性和地震動持續時間影響較小，但地震作用的最大軸力值仍受較大影響。

（2）三種地震波作用下，當視波速大于某值后，隨視波速的增加，各視波速下鋼桁架主梁桿件最大軸力值隨橋梁長度分布曲線較為集中，說明當視波速大于某值后，鋼桁架主梁桿件最大軸力值受視波速的影響較小，但各個地震波的臨界視波速值不同。

4 結 論

行波效應對于大跨度橋梁的影響不能忽視但仍無普遍性結論，且對公軌兩用獨塔單索面鋼桁梁斜拉橋行波效應分析研究極少。本文以某公軌兩用獨塔單索面鋼桁梁斜拉橋為背景，選取了三種加速度峰值、頻譜特性和持續時間不同地震波，從索塔最大彎矩和位移以及鋼桁架主梁的軸力和位移兩個方面研究了行波效應對獨塔單索面鋼桁架斜拉橋的影響，得出以下結論：

（1）加速度峰值相同，但頻譜特性和持續時間不同的地震波作用下索塔最大位移沿塔高分布規律和鋼桁架主梁桿件最大位移沿橋梁長度分布規律不同。

（2）地震作用下索塔最大彎矩隨塔高分布規律和主梁桿件最大軸力沿橋梁長度分布規律受頻譜特性和地震動持續時間影響較小，但頻譜特性和地震動持續時間對地震作用下索塔高度對應的最大彎矩值和橋梁長度對應的主梁桿件最大軸力值影響較大。

（3）行波效應分析時，應選取多個與場地相匹配的地震波，或對地震波進行一些參數的調整，以適應場地；當視波速較小時，地震波到達橋梁各墩的時間差較大，即使是非敏感因素在低波速下也會表現得不穩定，值得重視。