基于類PUSHOVER法的超高層建筑群震害預測

周 穎 王憶初 周廣新 周伯昌

（1.同濟大學土木工程防災國家重點實驗室，上海 200092；2.上海市地震局，上海 200062；3.上海佘山地球物理國家野外科學觀測研究站，上海 200062）

1 應用背景

大城市中人員和社會財富高度集中，基礎設施林立，新老建（構）筑物并存，呈現復雜、多樣、密集的發展趨勢。［1］一旦遭遇較大破壞力的地震災害，將會引起建筑功能退化，甚至影響人們的正常生活，造成經濟損失；尤其是超高層建筑的震害會造成極大的社會影響。為保證災前對整個城市建筑群的抗震能力有一個宏觀認識，災后能夠有序進行救災規劃部署，應做好城市建筑抗震韌性評價。建筑抗震韌性評價是指在設定水準地震作用后，維持和恢復原有建筑功能的能力。［2］評價一幢建筑在地震作用下是否能維持其建筑功能，主要依靠對建筑進行震害預測。在城市建筑群中，對砌體結構、鋼筋混凝土框架結構進行震害預測已經有大量實用的方法，對于結構復雜、容積率高、建造費用高昂的超高層建筑群的震害預測研究還很少。因此本文旨在提出一種定量化、普適化的方法進行城市中超高層建筑群的震害預測。傳統的單體震害預測方法包括歷史震害統計法、專家評估法、半經驗半理論法。［3］這些方法均需要大量的建筑震害數據，而超高層建筑還沒有大量系統的震害數據。目前對超高層建筑進行震害預測主要采用精細化建模方法。一方面大量的超高層建筑詳細資料收集困難，對超高層建筑進行精細化建模復雜費時，無法將其作為對大量的超高層建筑進行快速震害預測的方法。另外對大片區域超高層建筑群進行震害預測的主要目的不是獲得詳細精確的結構受力與變形結果，而是通過一種快速、適用、安全的評估方法對某區域超高層建筑群整體抗震能力做出定量評價。綜上，本文根據美國聯邦應急管理署HAZUS手冊［4］中的能力譜法，結合我國抗震設計規范提出了一種類PUSHOVER方法預測超高層建筑群地震震害，并對7度多遇地震、7度設防地震及7度罕遇地震作用下上海市150 m以上的超高層建筑群整體抗震能力進行定量評估。

2 震害預測方法

2.1 方法理論基礎

HAZUS方法是一種類PUSHOVER方法，將結構簡化成的多質點體系等效為單質點體系，以超高層建筑常見的結構形式框架-剪力墻結構為例，如圖1所示。以在單質點體系的譜位移-譜加速度（Acceleration-Displacement Response Spectra）格式下求得的能力譜曲線與需求譜曲線的交點作為評估建筑抗震能力的性能點，該性能點代表建筑物所能承受某烈度地震作用相應的最大位移。該法由于將結構等效為單質點體系，性能點的位移表示結構頂部最大位移。評價結構破壞狀態本應采用層間位移角，考慮到計算結果的實際意義，為估計結構的破壞狀態，假設每層結構的層間位移角均達到規范規定的限值，將結構層間位移角限值乘上結構高度和折減系數得到某破壞等級對應的結構頂部最大位移限值。根據性能點的位移與結構頂部最大位移限值，在統計意義上，給出建筑達到各種破壞等級的概率。依據HAZUS方法的原理，本文根據我國抗震設計規范構造能力譜、需求譜曲線，能力譜曲線按結構在多遇地震作用下的彈性設計計算構造；需求譜曲線按規范中相應烈度的彈性加速度反應譜構造，提出的類PUSHOVER方法適用于按照抗震設計規范設計的建筑。

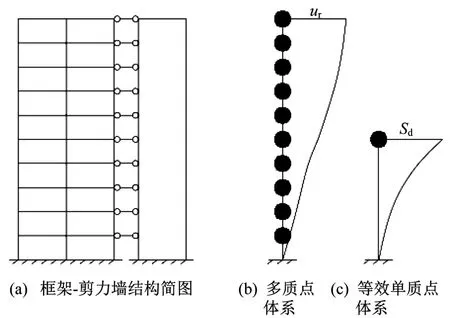
圖1 結構等效示意圖Fig.1 Equivalent schematic diagram of a structure

2.2 能力譜與需求譜

2.2.1 能力譜曲線構造

傳統能力譜曲線由單調水平荷載作用下的推覆曲線轉化得到，即將多質點體系的基底剪力與建筑頂層位移的關系等效為單質點體系的譜加速度與譜位移的關系。本方法能力譜曲線由結構的動力特征結合我國《建筑抗震設計規范》（GB 50011—2010）［5］直接構造而成。

根據振型分解法，j振型i質點的層間力Fij為

式中：γj為j振型的振型參與系數；Xij為j振型i質點的振幅；Saj為j振型的譜加速度；wi/g為第i層的質量；N為樓層數。

j振型結構底部剪力為Vj：

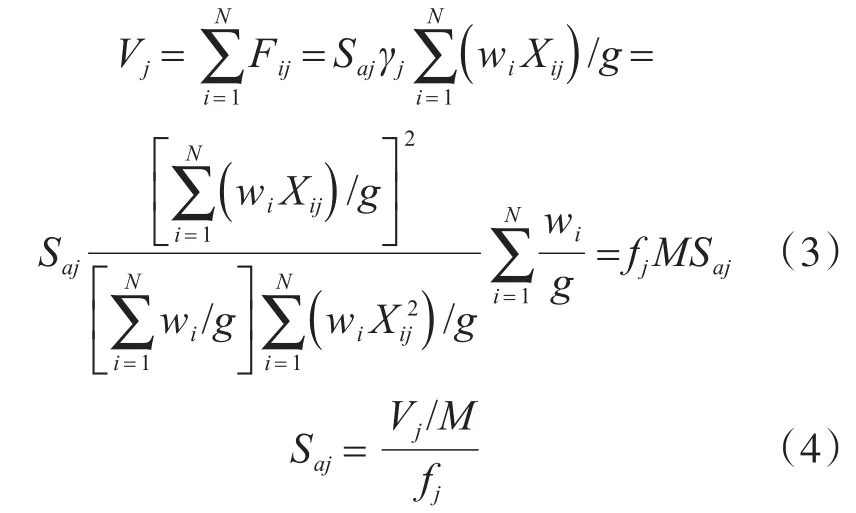
假定結構的地震響應以第一振型為主，且在整個地震作用過程中結構沿高度的側移可以用一個不變的形狀向量表示，這樣就可以將原結構等效為一個單自由度體系。該單自由度體系ADRS格式的譜加速度Sa和譜位移Sd為

式中：V為結構基底剪力；M為建筑物質量；fj為j振型的有效質量系數；ur為結構頂部位移。

根據假定結構第一振型的振型參與系數γ1=1，譜位移等于結構頂部位移。

由抗震設計規范知，結構底部剪力為FEk：

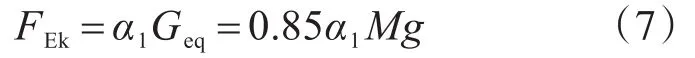
式中，α1為結構基本自振周期對應的地震影響系數，式（7）代入式（5）：

構造能力譜曲線時，需要兩個控制點（SDy，SAy）、（SDu，SAu），分別代表單質點體系屈服點與極限點的譜加速度與譜位移，作為能力譜雙折線的拐點。考慮設計強度富余，式（8）變為式（9）：

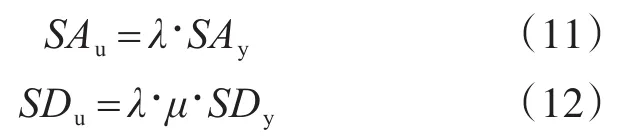
式中：κ為單質點體系屈服強度與設計強度之比；T1為建筑物基本自振周期，該周期為結構弱軸方向的周期（可由FEMA450［6］建議公式得到估算值T1=1.4Ct·hx）；Sa1為建筑基本自振周期T1對應的彈性加速度反應譜值；λ為單質點體系極限強度與屈服強度之比；μ為單質點體系延性系數。

根據我國《混凝土結構設計規范》（GB 50010—2010）［7］，考慮荷載分項系數與材料強度分項系數以及超高層建筑f1的范圍，確定SAy=1.7Sa1。對于鋼筋混凝土框架-剪力墻結構、框架-核心筒結構，極限強度與屈服強度之比λ可取2.5，延性系數μ可取3.0。

2.2.2 需求譜曲線構造

需求譜曲線根據單質點體系位移譜與擬加速度譜的關系［8］，由規范彈性加速度反應譜曲線直接轉化為譜加速度-譜位移曲線得到，見式（13）。小震作用于結構時，結構剛度退化效應不明顯，可不考慮彈性需求譜的折減。進行罕遇地震作用下的震害預測時，構造需求譜曲線時可以考慮引入彈塑性反應譜［9］對需求譜曲線進行修正。

由能力譜與需求譜的交點得到給定地震作用下單質點體系的譜位移Sd，即結構頂部最大位移ur，如圖2所示。

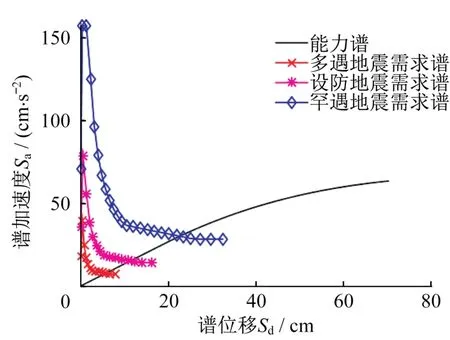
圖2 能力譜與需求譜示意圖Fig.2 Capacity spectrum and demand spectrum

2.3 破壞等級概率計算

根據《建筑物地震破壞等級劃分》（GB/T 24335—2009）［10］，本文將建筑物破壞等級劃分為5級，包括基本完好、輕微破壞、中等破壞、嚴重破壞以及毀壞。輕微破壞指結構基本使用功能不受影響；中等破壞指結構基本使用功能受到影響，修理后可使用；嚴重破壞指結構部分功能喪失，難以修復；毀壞指結構使用功能喪失，無法修復。用統計概率方式評估建筑物達到各破壞等級的可能性。

用譜位移Sd表示給定地震作用下建筑物的反應，假定某個破壞等級對應的譜位移-Sdj是對數正態分布，在給定譜位移Sd的條件下，可求出震害落入或超過某個破壞等級的累計概率Pc。

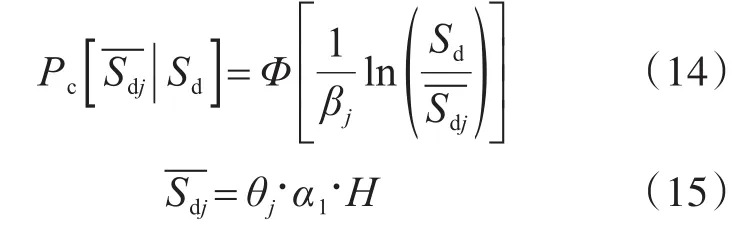
式中：Φ為標準正態累積分布函數；βj為考慮地震作用、建筑抗力變異性及譜位移估值不確定性的對數正態標準差；θj為某破壞等級對應的層間位移角均值；α1為高度系數；H為建筑高度。

根據累計概率Pc計算不同地震烈度下超高層建筑的易損性矩陣，即超高層建筑處于基本完好（N）、輕微破壞（S）、中等破壞（M）、嚴重破壞（E）和完全破壞（C）的概率P。

根據《建筑抗震設計規范》規定的彈性層間位移角限值1/800和彈塑性層間位移角限值1/100，確定各破壞等級對應的層間位移角均值θj，見表1。本文認為結構的破壞等級，即基本完好（輕微破壞）、中等破壞、嚴重破壞分別對應規范中要求的小震不壞、中震可修、大震不倒。

表1 各破壞等級對應的層間位移角均值Table 1 Mean value of story drift ratio corresponding to each damage grade

2.4 方法程序化及準確性驗證

基于上述理論編制類PUSHOVER法的MATLAB程序（1主程序+4子程序），實現建筑數據的自動讀取、建筑易損性矩陣的計算與計算結果輸出。程序框圖如圖3所示。

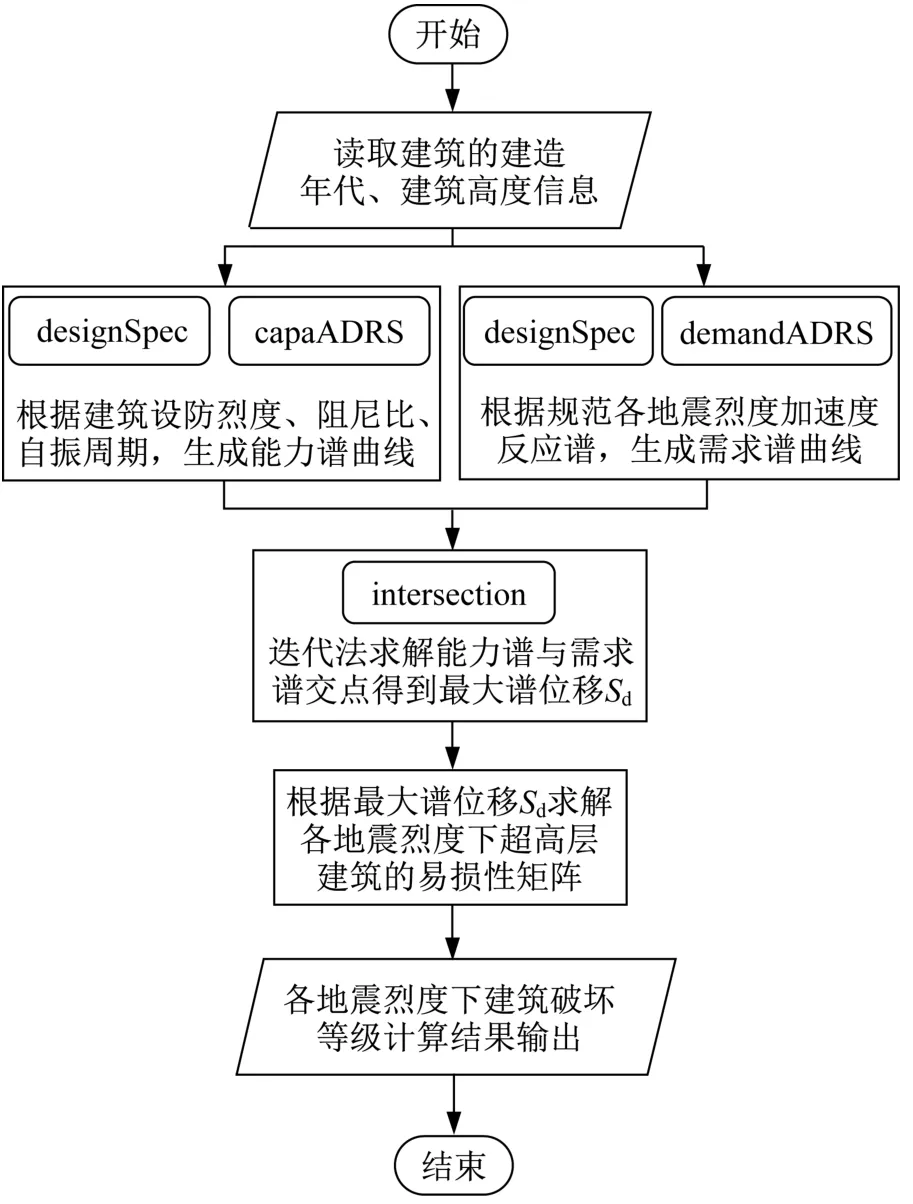
圖3 類PUSHOVER法MATLAB程序框圖Fig.3 MATLAB program diagram of PUSHOVER-like method

利用編制的MATLAB程序進行超高層建筑不同地震烈度下的震害預測。為驗證該方法的適用性和合理性，本文選取兩幢設防烈度為7度、高度分別為250 m［11］和632 m的建筑［12］，將其7度多遇地震、7度設防地震、7度罕遇地震作用下建筑頂部位移的類PUSHOVER法計算結果與參考文獻［11-12］中的有限元法計算結果進行比較，見表2。

表2 類PUSHOVER法與有限元法計算的建筑頂部位移Table 2 Building roof displacement calculated by PUSHOVER-like method and finite element method

7度多遇地震及7度設防地震作用下，兩種方法計算的建筑頂部位移差值較小；7度罕遇地震作用下，建筑頂部位移的類PUSHOVER法計算結果較有限元法偏大，因為兩幢建筑均按7度多遇地震下的彈性設計計算構造能力譜曲線，低估結構實際承載能力。計算結果表明，7度多遇地震及7度設防地震作用下，該類PUSHOVER方法與有限元法計算的建筑頂部位移基本相同，震害預測結果一致；7度罕遇地震作用下，類PUSHOVER方法較有限元法計算結果偏大，震害預測結果偏安全。因此本方法適用于150 m以上超高層建筑不同地震烈度下的震害預測。

3 超高層建筑震害預測

3.1 超高層建筑分布

根據世界高層建筑與都市人居學會（Council on Tall Buildings and Urban Habitat，CTBUH）全球高層數據庫統計［13］，截至2020年9月，上海市擁有GPS坐標記錄的150 m以上已建成的超高層建筑共164幢，建筑分布如圖4所示。其中250m以下的建筑約占90%，結構形式多為框架-剪力墻結構及框架-核心筒結構，均為抗側力性能良好的結構形式。

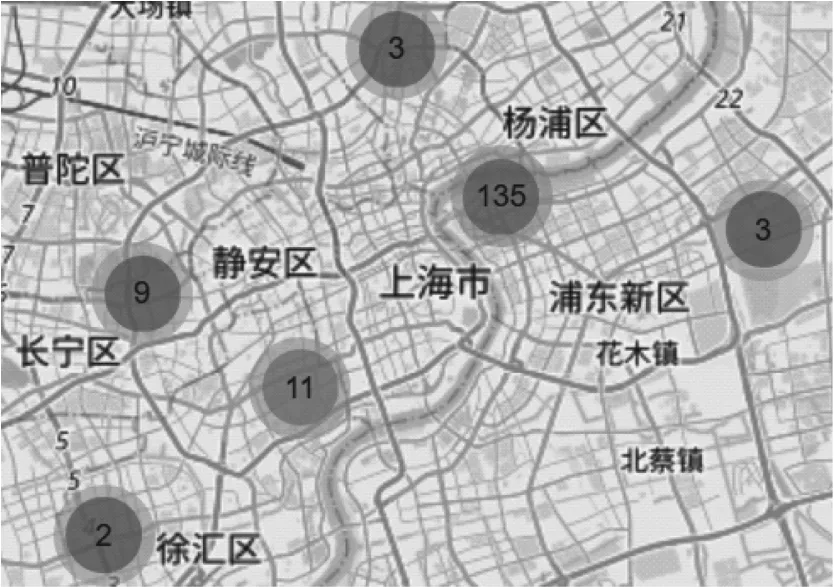
圖4 上海市150 m以上超高層建筑分布圖Fig.4 Distribution of super high-rise buildings above 150 m in Shanghai

列舉164幢超高層建筑的基本信息，包括所屬區域、建筑年份、建筑高度，見表3。

表3 164幢超高層建筑基本信息［13］（CTBUH數據截至2020.09）Table 3 Architectural data of 164 super high-rise buildings（comes from CTBUH until 2020.09）

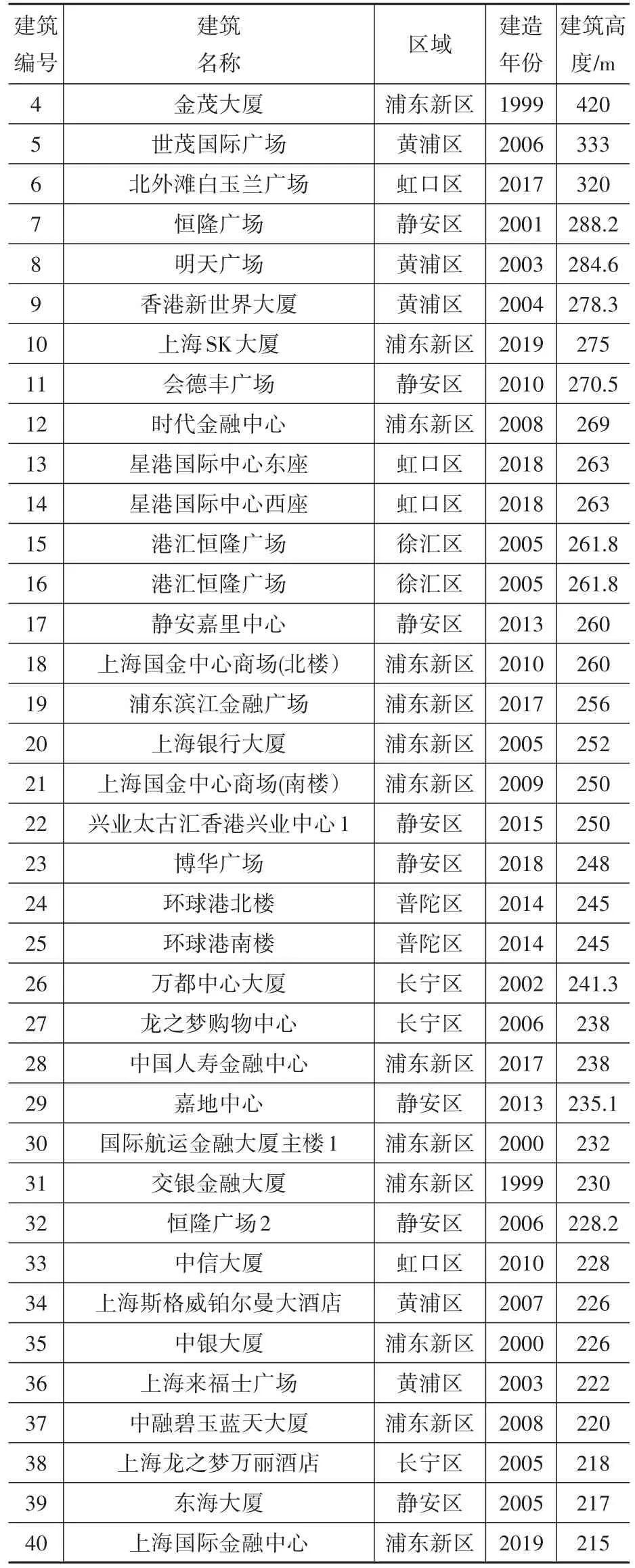
續表

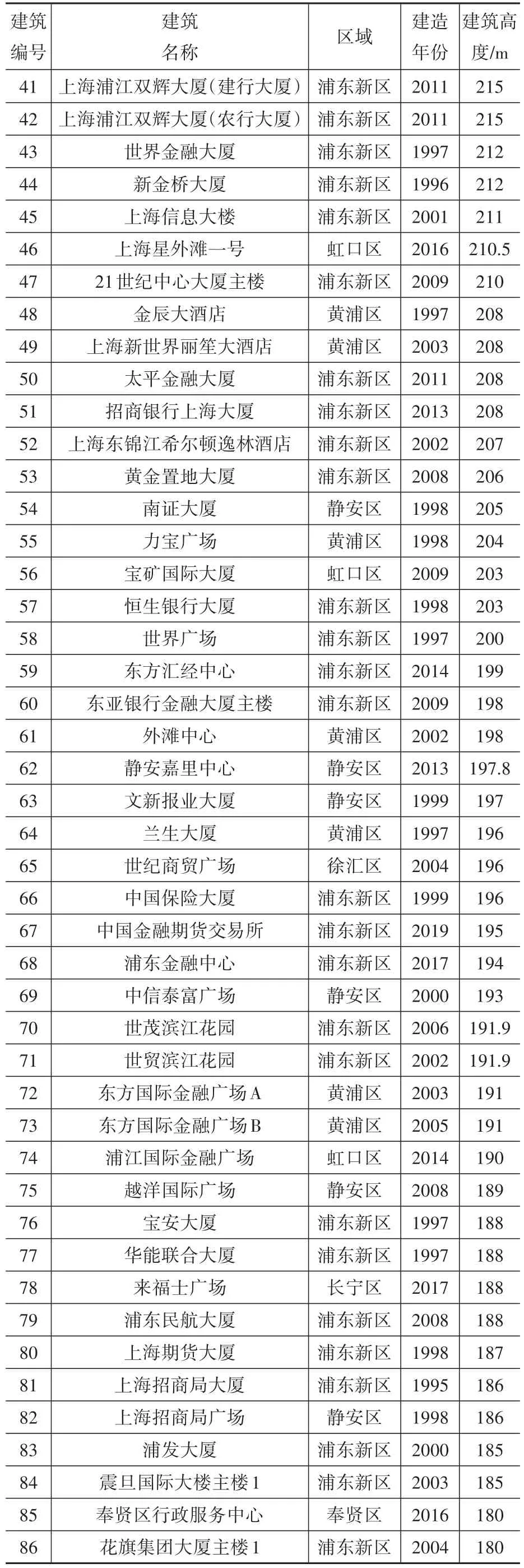
續表

續表

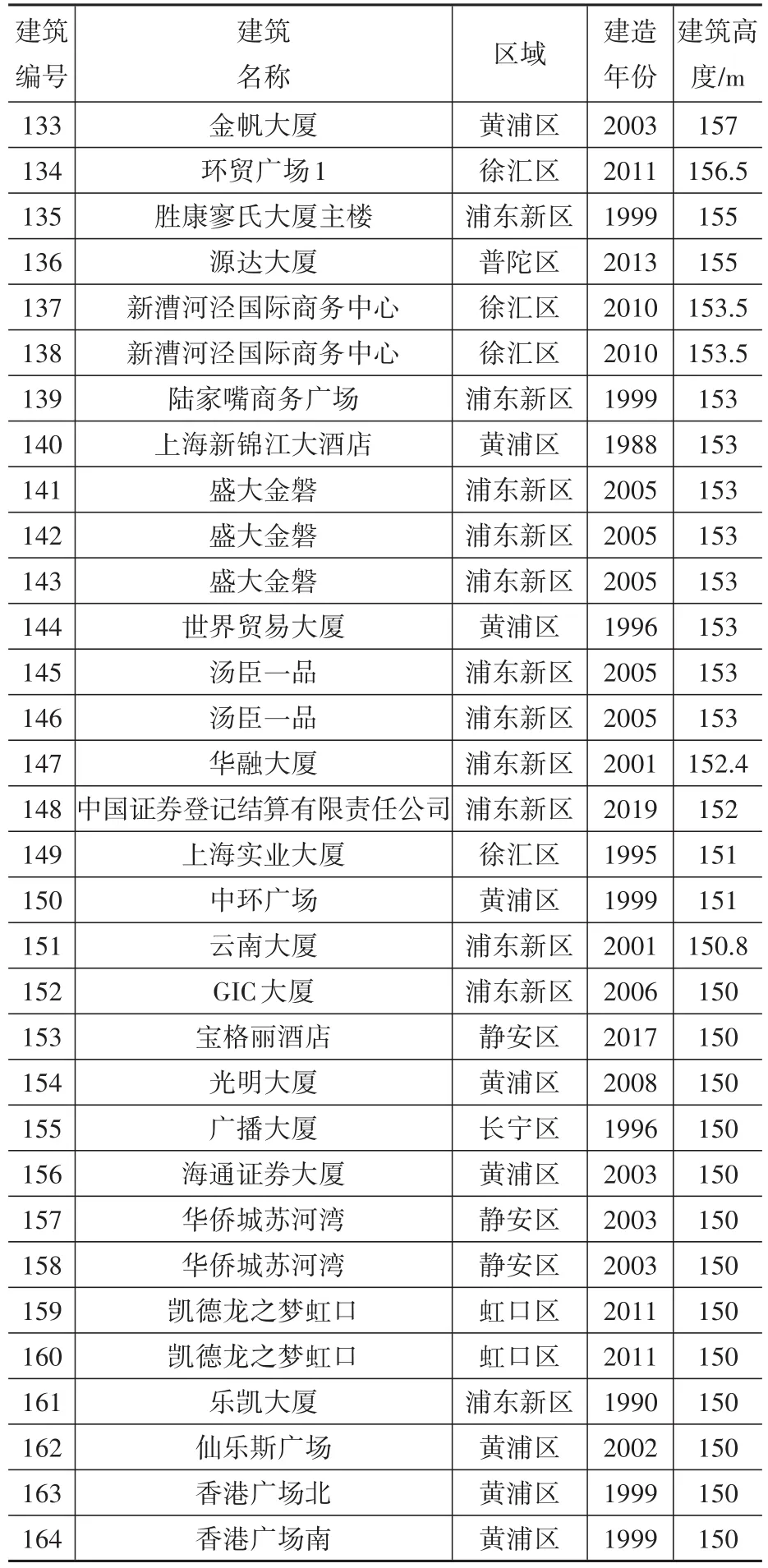
續表

3.2 超高層建筑震害預測

考慮到超高層建筑高度多為250 m以下，且上文中驗算高度為250 m超高層建筑的類PUSHOVER法和有限元法建筑頂部位移計算結果差值較小，故選取250 m的超高層建筑作為個例說明震害預測過程。利用編制的MATLAB程序計算高度為250 m超高層建筑的易損性矩陣，見表4。在某一地震烈度下，最大概率發生的破壞狀態即為某建筑的預測破壞狀態。根據易損性矩陣數據進行震害預測，在7度多遇地震、7度設防地震及7度罕遇地震作用下，該建筑分別處于基本完好、輕微破壞和毀壞狀態。

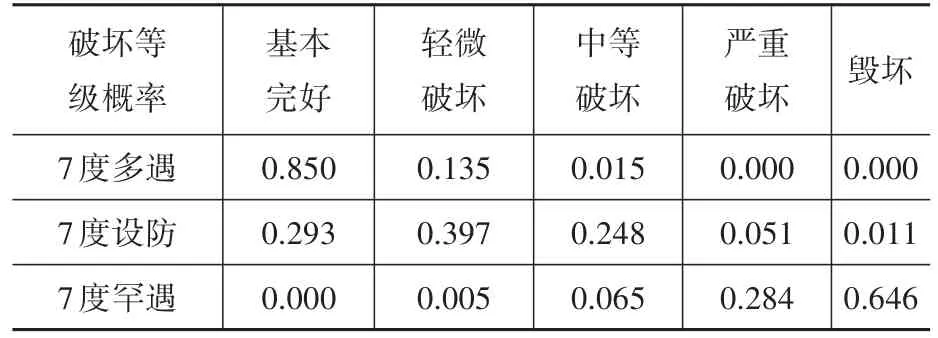
表4 H=250 m建筑易損性矩陣Table 4 Vulnerability matrix of a 250 m building

根據本方法，對普查得到的信息完整的上海市164幢高度150 m以上的建筑進行快速震害預測，MATLAB程序計算某烈度下每幢建筑破壞狀態計算機運行時間約為1 min。選取8幢典型建筑的震害預測結果，見表5。

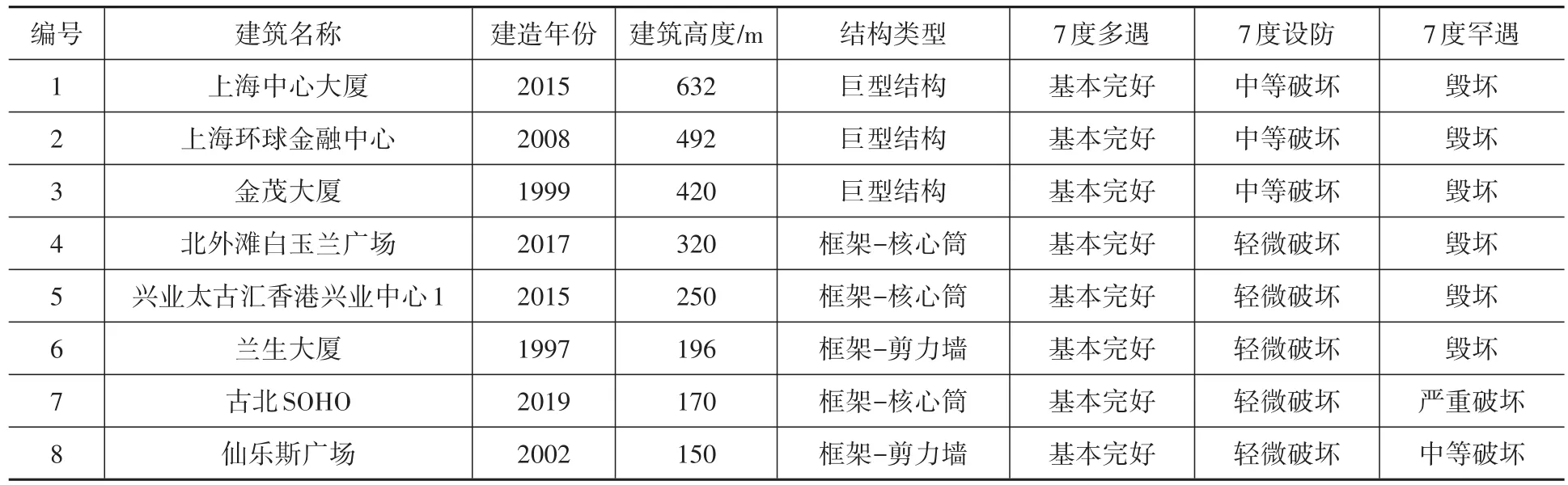
表5 上海市8幢典型超高層建筑震害預測結果Table 5 Seismic damage prediction results of 8 typical super high-rise buildings in Shanghai

在164幢超高層建筑震害預測結果基礎上，歸納統計出上海市150 m以上超高層建筑群在7度多遇地震、7度設防地震及7度罕遇地震作用下的易損性矩陣，見表6。

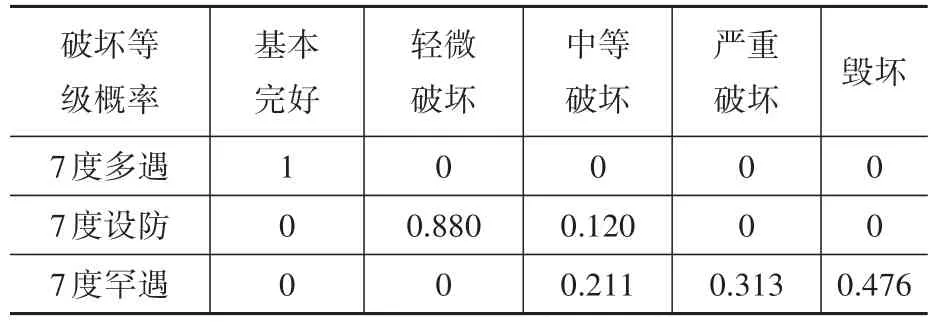
表6 上海市150 m以上超高層建筑群易損性矩陣Table 6 Vulnerability matrix of high-rise buildings above 150 m in Shanghai

3.3 震害預測結果分析

根據表6上海市超高層建筑群易損性矩陣結果可知，按上海市7度設防烈度設計的超高層建筑，在7度多遇地震作用下，均處于基本完好狀態；在7度設防地震作用下，約90%的超高層建筑發生輕微破壞，其余建筑發生中等破壞，發生中等破壞的結構均為2003年及以前建成的建筑及建筑高度大于400 m的建筑。在7度罕遇地震作用下，2003年以前建成且高度大于155 m的超高層建筑均發生毀壞，其余超高層建筑發生中等破壞；2003年以后建成建筑，高度小于160 m的超高層建筑發生中等破壞，高度大于160 m且小于220 m的超高層建筑發生嚴重破壞，其余超高層建筑發生毀壞。

震害預測結果表明滿足規范中小震不壞、中震可修的要求，超過50%的建筑滿足大震不倒的要求。考慮到計算結果偏安全，上海市150 m以上的超高層建筑群在7度多遇地震、7度設防地震、7度罕遇地震作用下抗震性能良好。

4 結 論

本文提出了一種結合中國抗震設計規范的類PUSHOVER法對上海市150 m以上的超高層建筑進行不同地震烈度下的震害預測。根據類PUSHOVER法與有限元法所計算建筑頂部位移的一致性并且各建筑與算例建筑結構形式普遍相同，表明該方法可以大量、快速、安全地進行超高層建筑群震害預測。

震害預測結果表明，按上海市7度設防烈度設計的150 m以上超高層建筑，在7度多遇地震作用下，均處于基本完好狀態；在7度設防地震作用下，約90%的超高層建筑發生輕微破壞，其余建筑發生中等破壞；在7度罕遇地震作用下，約80%的超高層建筑發生嚴重破壞或毀壞。因此，上海市150 m以上超高層建筑滿足規范中小震不壞、中震可修、大震不倒的要求。

該方法利用計算建筑頂部位移的宏觀方法進行建筑震害狀態評估，最終通過不同地震烈度下建筑處于基本完好至毀壞這5種破壞等級中的一種來評價建筑維持其建筑功能的能力。可以將該類PUSHOVER方法與彎剪層間模型法［14］、精細化建模法等結合使用，納入不同精度模型建筑抗震韌性評價體系。

另外，可以采用地理信息系統（GIS）快速準確地獲取建筑數據并實時更新，保證震害預測的時效性；根據類PUSHOVER方法計算結果，通過城市仿真系統清晰直觀地展示超高層建筑群的震害情況，有利于了解其地震成災機理，［15］為災前建筑加固、災后建筑維修提供數據理論支持。

本文提出的方法適用的建筑高度范圍廣泛，可完成多層、高層至超高層建筑的震害預測。通過修改類PUSHOVER法中的參數使其適用于不同高度及年代的建筑，可將本方法推廣用于城市框架、剪力墻等建筑整體抗震能力評估及其程序化實現。