隨機地震激勵作用下自復位結構的平穩響應

胡慧瑛，陳林聰,2

(1.華僑大學 土木工程學院，福建 廈門 361021；2.福建省智慧基礎設施與監測重點實驗室，福建 廈門 361021)

地震對人類社會的危害不言而喻。傳統結構雖然能有效保障人員的生命財產安全，但震后往往存在結構倒塌、殘余變形過大等問題，使得結構震后修復成本過高。近來，為了減少結構震后修復產生的經濟損失，工程界致力于研究可恢復功能結構[1-5]。可恢復功能結構是指在震中不發生破壞或是僅發生可以迅速修復破壞的結構，因此能顯著減小震后修復所需的時間成本和經濟成本。自復位結構作為可恢復功能結構中的一種，逐漸成為國內外學者的研究熱點。已有研究表明，自復位結構不僅具有與傳統結構大致相當的耗能能力，還能有效消除結構的殘余變形，大大減小了結構震后修復負擔。

目前有關自復位結構的研究成果豐碩。在響應預測方面，常用方法有時程分析法[6-7]以及平均法[8-9]，但這些研究多是在確定性激勵下進行，鮮有涉及隨機激勵環境。眾所周知，地震地面運動具有明顯的隨機性。在隨機地震動作用下自復位系統的響應也是一個隨機過程。最近，胡曉斌等[10]利用等效線性化法建立了單自由度自復位系統隨機地震響應的求解流程。然而，等效線性化僅能獲得系統的高斯響應，低估了響應位移與速度的均方值，以致結果偏于不安全。另外，上述研究中采用了高斯白噪聲激勵模型，該激勵能量在頻域內是均勻分布的，有悖于實際情況[11]。因此，非常有必要發展一種更有效的方法來確定自復位系統的隨機地震響應，同時亦需引入一種能更好模擬地震作用的數學模型。

隨機平均法是將隨機平均原理與FPK方程法相結合的一類方法。該法是分析非線性隨機系統最有效的方法之一。近年來，隨機平均法被廣泛的運用于非線性系統與隨機參激系統的隨機響應預測、可靠性估計及隨機穩定性判別。Roberts和Spanos[12]以及朱位秋[13]等均對隨機平均法的應用發展做出了嚴謹的綜述。隨機平均法最突出的優點是可以降維，從而降低求解FPK方程的難度，特別是對于擬不可積哈密頓系統[14]，平均后的系統是一維的。與等效線性化方法相比，隨機平均方法還具有克服概率密度不準確、保持原系統主要非線性特征等顯著優點。

國內外學者相繼提出多種過濾白噪聲模型來模擬地震作用，目前常用分析譜模型有杜修力譜[15]、歐進萍譜[16]、金井清譜[17]等。金井清過濾白噪聲模型是在白噪聲模型的基礎上，進一步考慮地表土層特性對地震動頻譜特征的影響，物理意義明確且能較好地模擬地震地面運動特性，在實際中得到廣泛應用。本文考慮到地震動的隨機性，應用隨機平均法研究了金井清過濾白噪聲激勵下單自由度自復位系統的平穩響應。首先利用廣義諧波平衡技術，將旗幟形的恢復力解耦為幅值依賴的等效擬線性彈性力和擬線性阻尼力，得到原系統的等效非線性系統；然后，應用基于廣義諧和函數的隨機平均法將等效非線性系統簡化為關于系統幅值的平均伊藤方程，建立并求解與之相應FPK方程得到系統幅值的穩態概率密度函數；研究系統關鍵參數對系統響應的影響，并通過蒙特卡羅模擬對理論解析結果進行驗證。

1 隨機地震荷載作用下單自由度自復位系統

隨機地震荷載作用下單自由度自復位系統的運動微分方程可以表示為，

(1)

(2)

式中:ωg、ξg分別為地震波傳播過程中所經歷土層的特征頻率和阻尼比；S0為位于震源處的基巖傳給上層的白噪聲功率譜密度；該模型的自復位體系的恢復力常用FS(Flag-shaped)模型描述，如圖1(a)所示，由圖1可得，自復位體系恢復力可以分解為彈性力(圖1(b))和滯變力(圖1(c)),即

(a)旗幟形恢復力模型

(3)

式中：Z是滯變位移，α為能量耗散系數。

如圖2所示，滯變位移Z可以分段表示為，

圖2 自復位體系滯變位移

(4)

(5)

式中：β、Xy、A分別表示能量耗散系數、屈服位移和系統位移幅值。

將式(4)、(5)代入式(3)中，恢復力的表達式可整理為，

(6)

(7)

2 等效非線性系統

由圖1可知，式(6)與(7)中表示的恢復力同時影響系統的阻尼和剛度。根據廣義諧波平衡技術，恢復力可解耦為幅值依賴的等效擬線性彈性力和擬線性阻尼力，

(8)

式中：

(9)

(10)

將式(8)代入式(1)，可得系統(1)的等效非線性系統，

(11)

系統(11)的總能量為，

(12)

式中：

(13)

3 隨機平均

假設系統(11)解的形式為，

Y(t)=A(t)cosΘ(t)

(14)

式中：

Θ(t)=Φ(t)+Γ(t)

(15)

變量A(t)、Θ(t)與Г(t)均為隨機過程。

(16)

(17)

式中：

(18)

當阻尼和激勵較弱的時候，根據Stratonovich-Khasminskii極限定理[17],A,Г弱收斂于二維擴散Markov過程。需指出的是，關于A(t)的平均伊藤隨機微分方程中不含Г(t)。關于A(t)的平均伊藤隨機微分方程為，

(19)

式中：B(t)為單位維納過程；平均漂移和擴散系數分別為，

(20)

式中R(τ)表示系統激勵的自相關函數；〈·〉Θ表示對Θ作平均，即

(21)

為了進一步獲得漂移與擴散系數的表達式，現將Gik展開為Fourier級數

Gik=Gik0(A)+

(22)

將式(22)代入式(20)，完成對τ的積分和對Θ的平均后，得

(23)

支配轉移概率密度p(a|a0;t)滿足的FPK方程為，

(24)

初始條件為，

p=δ(a-a0)

(25)

式中:a為系統幅值，a0為系統初始幅值。

當?p/?t=0時，方程(22)有如下的平穩精確解，

(26)

式中,C0為歸一化常數。

4 參數分析

本節考察能量耗散系數β、屈服位移Xy和激勵強度D1取值的變化對系統穩態概率密度函數的影響。選取系統參數為：c=0.05、α=0.2、ωg=10、ξg=0.9、D1=0.01。其中實線表示由方程式(26)得到的數值解結果，符號(△,□,◇)表示對原方程(1)直接進行蒙特卡羅的結果。觀察每幅圖像都可以看出理論解和蒙特卡羅解在誤差允許范圍內吻合，表明文中提出的求解方法有效。

圖3～5給出了當能量耗散系數β=0.5，β=1.0與β=2.0時，屈服位移Xy取值的變化對系統響應的影響。從這三個圖中均可看出，當Xy<1.0時，p(a)隨著Xy的減小向左偏移并在較小a處達到峰值。這說明屈服位移的降低可有效減小系統響應。該現象可用圖8來解釋，當能量耗散系數一定時，隨著Xy的減小，滯回曲線的面積增大，即系統的耗能性能提高。而當Xy>1.0時，Xy的減小并不能有效的減小系統響應。此外，由于旗幟形恢復力是分段函數，當Xy=1.0時，p(a)在分段點a=Xy處存在不光滑現象，該現象β=2.0時最為明顯,見圖5。

圖3 β=0.5時系統關于幅值的穩態概率密度函數

圖4 β=1.0時系統關于幅值的穩態概率密度函數

圖5 β=2.0時系統關于幅值的穩態概率密度函數

圖6中，研究了屈服位移Xy=0.5時，能量耗散系數β對系統穩態響應的影響。由圖6可看出，β的變化對系統的穩態響應的大小影響不大，但隨著β的增加，p(a)逐漸接近于正態分布，與此同時，p(a)在分段點處不光滑現象越來越明顯。

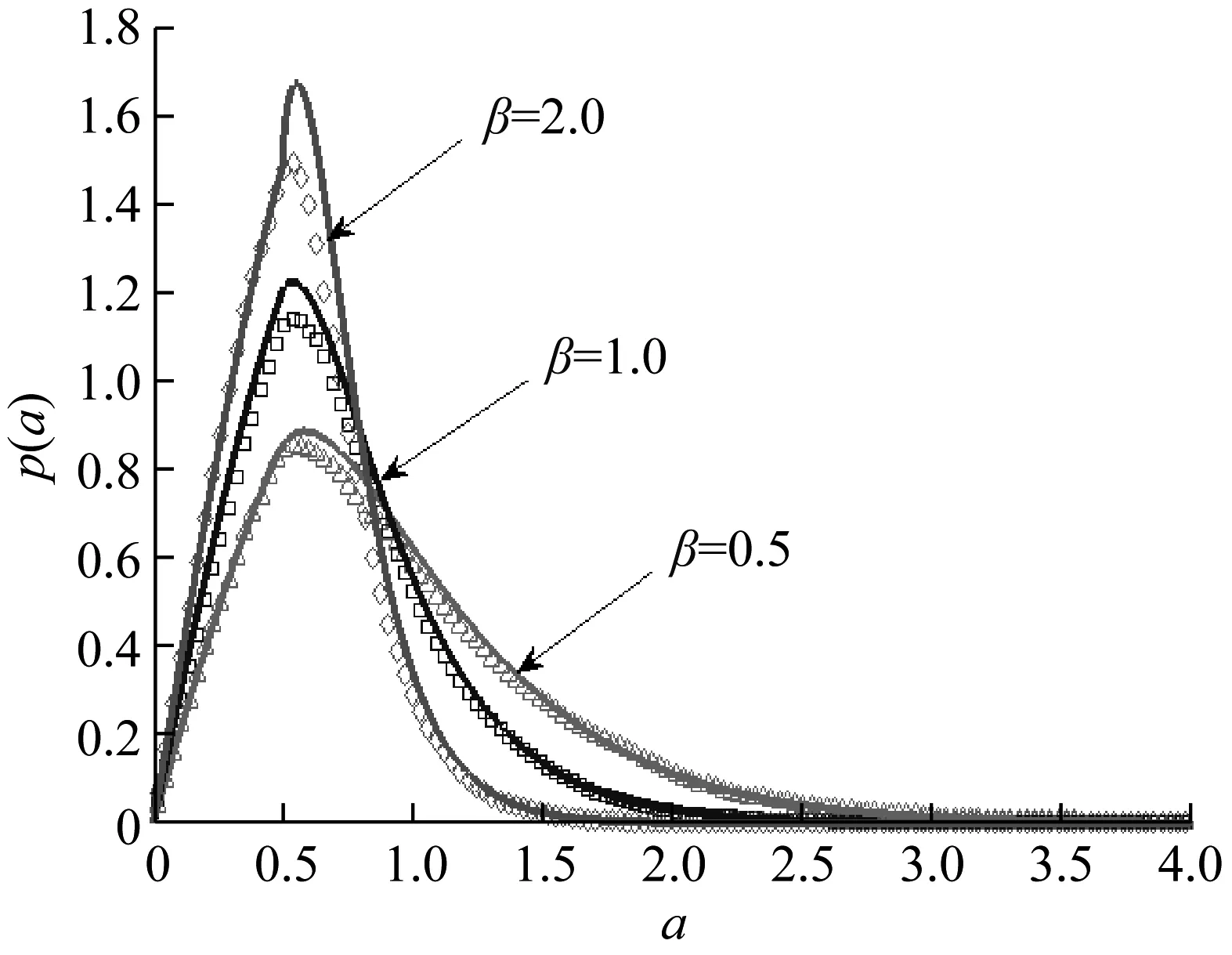
圖6 Xy=0.5時系統關于幅值的穩態概率密度函數

圖7中，研究了屈服位移Xy=1.0且能量耗散系數β=1.0時，激勵強度D1對系統穩態響應的影響。從圖7可看出，理論解和蒙特卡羅解吻合的非常好。

圖7 Xy=1.0,β=1.0時系統關于幅值的穩態概率密度函數

圖8 β=0.5時旗幟形滯回曲線所圍面積

5 結 論

本文研究了基于金井清譜隨機地震激勵下單自由度自復位體系的平穩響應。運用廣義諧波平衡技術，得到原系統的等效非線性方程。通過van der Pol變換和隨機平均法，得到關于系統幅值的平均伊藤方程。建立并求解相應的FPK方程，獲得關于幅值的穩態概率密度函數，研究了能量耗散系數和屈服位移對系統穩態響應的影響。研究結論如下：

(1)當屈服位移小于1.0時，系統的穩態響應隨著屈服位移的減小而降低；

(2)由于系統恢復力是分段函數，系統的穩態響應在分段點處存在不光滑現象，該現象在屈服位移為1.0且能量耗散系數為2.0時尤為明顯；

(3)通過與蒙特卡羅模擬結果的對比發現理論解析解具有很好的精度。

附錄A

系統(1)解的形式可以假設為以下廣義諧波方程

X(t)=A(t)cosΘ′(t)

(A1)

對于A≤Xy,

(A2)

(A3)

對于A>Xy,

(A4)

(A5)

其中