高溫吸熱管內超臨界CO2 傳熱特性的數值模擬*

莊曉如 徐心海 楊智 趙延興 余鵬?

1) (南方科技大學力學與航空航天工程系,深圳 518055)

2) (哈爾濱工業大學 (深圳)機電工程與自動化學院,深圳 518055)

3) (廣東工業大學材料與能源學院,廣州 510006)

4) (中國科學院理化技術研究所,中國科學院低溫工程學重點實驗室,北京 100190)

研究超臨界CO2 在高溫吸熱管內的傳熱特性是將其應用于聚光太陽能熱發電技術中的基礎.本文對此進行了數值模擬研究,分析了流體溫度、流動方向、系統壓力、質量流率和熱流密度對對流傳熱系數和Nu 數的影響.結果表明: 高溫區 (800—1050 K) 的對流傳熱系數和Nu 數受流動方向和系統壓力的影響均很小,但都隨著質量流率的增大以及熱流密度的減小而明顯增大; 而隨著流體溫度的升高,對流傳熱系數近似線性增大,Nu 數則近似線性減小.另外,本文研究發現在高溫區可忽略浮升力對傳熱的影響,而由高熱流密度引起的流動加速效應會明顯惡化傳熱.最后,選取了八種管內超臨界流體傳熱關聯式與模擬結果進行對比,發現使用基于熱物性修正的關聯式對高溫區傳熱數據預測的結果優于使用基于無量綱數修正的關聯式得到的結果,且其中預測效果最優的關聯式得到的計算結果與模擬結果之間的平均絕對相對偏差為8.1%.

1 引 言

近年來隨著聚光太陽能熱發電技術的不斷發展,工程上對其傳熱流體提出了更高的要求.CO2具有來源廣泛、化學性質穩定、無毒害等優點,并且在超臨界狀態 (Tc= 304 K,pc= 7.4 MPa) 下具有優越的傳熱特性[1].同時,超臨界CO2布雷頓循環在773—973 K 溫區的循環熱效率明顯高于蒸汽動力循環在此溫區的循環效率[2?4].因此,超臨界CO2有潛力作為高溫傳熱流體應用于聚光太陽能熱發電站中[5,6].美國能源部在第三代聚光太陽能熱發電技術路線的報告中也提出,超臨界CO2可作為新型高溫傳熱流體應用于熱發電站的吸熱器中,并指出開發新型高溫傳熱流體的目標之一是使其在吸熱器出口溫度超過993 K[7].

深入認識超臨界CO2在高溫區的管內傳熱特性是將其應用于聚光太陽能熱發電技術中的基礎,然而目前關于其管內傳熱特性的實驗和數值模擬研究均大多集中在近臨界點溫區[8,9].Kim 等[10]對超臨界CO2在垂直管內徑為4.5 mm、入口溫度范圍為302—388 K、系統壓力范圍為7.5—10.3 MPa、質量流率范圍為208—874 kg·m–2·s–1和熱流密度范圍為38—234 kW·m–2的工況下進行了對流傳熱實驗,研究了熱流密度和質量流率對管壁面溫度分布的影響.在向上流動、熱流密度適中以及質量流率較低時,壁面溫度有明顯的峰值; 在向下流動時,所有工況下壁面溫度沿流動方向均單調增加; 浮升力和流動加速效應對傳熱有明顯的影響,并考慮了兩者的作用提出了新的傳熱關聯式.Bovard 等[11]模擬研究了超臨界CO2在垂直管內徑為4.5 和6.3 mm、入口溫度為302 K、系統壓力范圍為6.5—8.3 MPa、質量流率范圍為51—236 kg·m–2·s–1和熱流密度范圍為52—85 kW·m–2的管內傳熱特性,得到提高質量流率和系統壓力可削弱浮升力和流動加速效應對傳熱的影響,也提出了考慮兩種效應的新傳熱關聯式.

然而,將超臨界CO2作為傳熱流體應用在塔式聚光太陽能熱發電站中,其吸熱器入口溫度通常要求高于773 K,目前鮮少有關于高溫區超臨界CO2管內傳熱特性研究的公開報道[8].Qiu 等[12]對超臨界CO2在槽式太陽能吸熱器中的傳熱特性進行了數值計算,所研究的入口溫度范圍為315—773.15 K、系統壓力為9 和20 MPa,結果表明浮升力作用使圓管橫截面出現了明顯的二次渦流現象,且近臨界點溫區的二次渦流速度比高溫區大一個數量級.劉占斌等[13]模擬研究了六種泡沫材料填充方式對吸熱管內超臨界CO2流動與換熱性能以及管壁溫度分布的影響.所研究的入口溫度為813 K、系統壓力為20 MPa 和熱流密度為500 kW·m–2,結果表明環形填充方式 (沿管內壁填充) 的流動換熱綜合性能最優、凈吸熱量最大、管壁最高溫度最低且溫度分布最均勻.

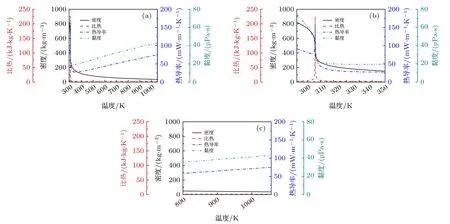
圖1 CO2 在p = 7.5 MPa 下的熱物性變化 (a) T = 293—1050 K; (b) T = 293—350 K; (c) T = 800—1050 KFig.1.Properties of CO2 at p = 7.5 MPa: (a) T = 293–1050 K; (b) T = 293–350 K; (c) T = 800–1050 K.

為了進一步研究超臨界CO2在高溫吸熱管內的傳熱特性,本文首先分析CO2在高溫區與近臨界點溫區的熱物性區別,再基于ANSYS FLUENT軟件建立吸熱管內超臨界CO2對流換熱的三維數值模型,分析流體溫度、流動方向、系統壓力、質量流率和熱流密度等工況條件對對流傳熱系數和Nu 數的影響規律,揭示不同工況條件下的傳熱機理.然后,判別浮升力和流動加速效應在高溫區對傳熱的影響情況,并與八種管內超臨界流體傳熱關聯式進行對比,找出預測效果較優的關聯式.研究結果可為超臨界CO2太陽能吸熱器的優化設計和安全穩定運行提供理論參考.

2 超臨界CO2 的熱物理性質

為了了解CO2在近臨界點溫區 (293—350 K)和高溫區 (800—1050 K) 的熱物性區別,圖1 給出了CO2在壓力7.5 MPa、溫度范圍293—1050 K下的密度、比熱、熱導率和黏度的變化情況[14].可見,CO2的熱物性在近臨界點溫區隨溫度劇烈變化,其中密度和黏度在臨界點附近急劇下降,比熱和熱導率則在臨界點附近出現極大值.而在高溫區,CO2的熱物性與近臨界點溫區相比變化不那么明顯 (特別是比熱),且熱導率和黏度在兩個溫區呈現相反的變化趨勢.這些因素均可能使超臨界CO2在兩個溫區呈現不同的傳熱特性.另外,圖2所示的是在高溫區不同臨界壓力 (7.5—9 MPa)下CO2熱物性的變化情況[14].可見,隨著壓力增大,各熱物性均有所提高,但除密度外,壓力對熱物性的影響均很小.

圖2 CO2 在高溫區T = 800—1050 K,p = 7.5—9 MPa 下的熱物性變化 (a) 密度; (b) 比熱; (c) 熱導率; (d) 黏度Fig.2.Properties of CO2 at high temperature region of T = 800–1050 K with p = 7.5–9 MPa: (a) Density; (b) specific heat;(c) thermal conductivity; (d) viscosity.

3 傳熱模型

3.1 數值模型

本文所研究的吸熱管,管徑為6 mm,管長為500 mm 的圓管,計算過程中忽略圓管壁厚,幾何模型如圖3 所示.

假設管內流動為穩態,忽略吸熱管與外界環境的換熱.對于高溫區超臨界CO2的流動傳熱數值計算,Qiu 等[12]和劉占斌等[13]的計算結果顯示,采用標準k-ε湍流模型[15]可獲得準確的計算結果.因此,本文采用標準k-ε湍流模型進行數值計算,模型的控制方程可表示如下.

質量方程:

動量方程:

能量方程:

湍動能k方程:

耗散速率ε方程:

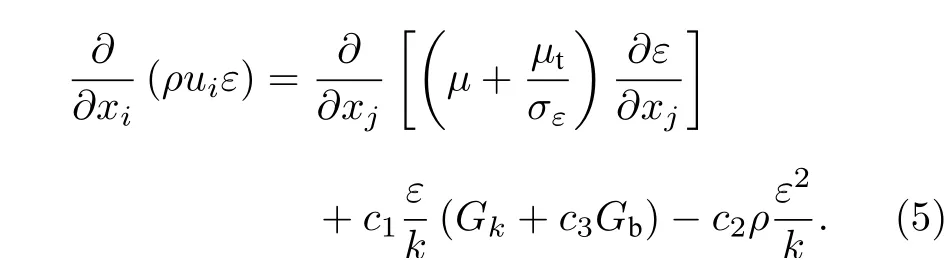
這里

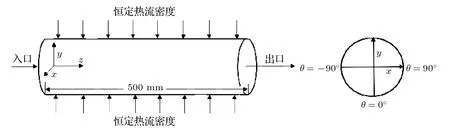
圖3 吸熱管幾何模型Fig.3.Geometric model of the solar receiver tube.

式中,ρ為密度 (kg·m–3);g為重力系數 (m·s–2);u為速度 (m·s–1);δij為克羅內克函數,當i=j時,δij= 1,當i≠j時,δij= 0;p為壓力 (Pa);μ為動力黏度 (Pa·s);μt為湍流黏度,μt=ρCμk2/ε;cp為比熱 (J·kg–1·K–1);k為湍動能;ε為耗散速率;T為溫度 (K);λ為熱導率 (W·m–1·K–1);β為熱膨脹系數 (K–1);σk和σε分別為湍動能和耗散速率對應的湍流普朗特數;c1,c2,Cμ,Prt均為模型經驗常數;湍流模型參數具體設置[12]為σk= 1.0,σε= 1.3,c1= 1.44,c2= 1.92,Cμ= 0.09,Prt= 0.85.

3.2 邊界條件和求解設置

模型的邊界條件設置如下.

1) 入口: 采用質量流量入口邊界條件,速度垂直于入口截面,流量研究范圍為G= 200—500 kg·m–2·s–1.

2) 出口: 采用壓力出口邊界條件,流動出口的絕對壓力研究范圍為p= 7.5—9 MPa.

3) 壁面: 設置為靜態無滑移邊界條件,給定恒定熱流密度,研究范圍為q= 100—800 kW·m–2.

使用ANSYS FLUENT 軟件進行吸熱管內超臨界CO2傳熱特性的數值計算,采用SIMPEC 算法求解速度與壓力的耦合方程,動量和能量方程采用QUICK 格式進行離散,湍動能和耗散速率方程采用二階迎風格式.模型中的CO2熱物性數據來自美國國家標準與技術研究所 (NIST) 的數據庫,通過在ANSYS FLUENT 中激活nist-real-gas-model功能進行直接調用.當各控制方程的殘差小于10–6,且出口流體溫度和壁面溫度沒有明顯變化,則認為計算收斂.

3.3 網格無關性驗證和模型驗證

圖4 吸熱管三維模型網格劃分 (網格數量: 841000)Fig.4.Mesh generation of the three-dimensional solar receiver tube (grid quantity: 841000).

采用ANSYS ICEM 軟件對圖3 吸熱管三維模型進行網格劃分,網格生成效果如圖4 所示.由于近壁面位置的溫度梯度和速度梯度較大,所以對近壁面處的網格進行了加密,保證近壁面處的無量綱壁面距離 (y+) 小于1.為了對計算網格進行無關性驗證,分別對比了網格數量為2652250,1332250,841000,462250 和196000 時 (網格質量均大于0.7),模擬所得的出口截面壁面溫度 (Tw,o) 和對流傳熱系數 (ho),如表1 所列.可見,算例1 和算例3 的Tw,o和ho相對偏差分別僅為0.07%和0.14%.因此,在同時考慮計算精度和運算時間的情況下,最終選擇了網格數量為841000 的網格進行后續的數值計算.其中,對流傳熱系數h和對應的努塞爾數Nu可由下式計算得到:

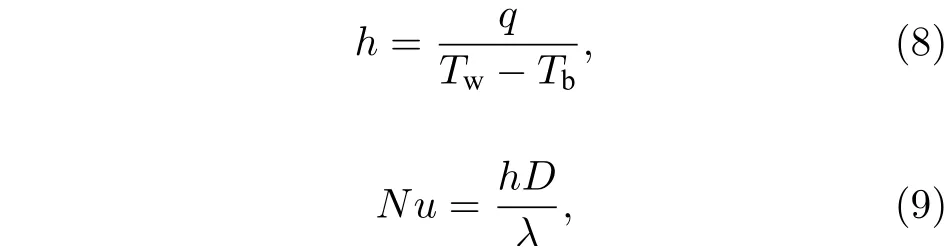
式中,q為壁面熱流密度 (kW·m–2);D為吸熱管直徑 (m);Tw為壁面溫度;Tb為流體溫度,可由下式計算得到

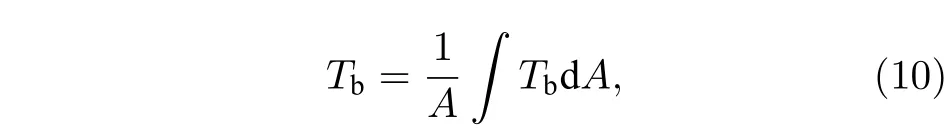
其中A為吸熱管橫截面流體面積 (m2).

表1 網格無關性驗證結果Table 1.Verification for grid independence.

另外,為了驗證模型的準確性,將三種工況條件下的計算結果與文獻[16]中相同工況條件下的實驗數據進行了對比,如圖5 所示.可見,三種工況條件的計算結果與實驗數據均符合較好,且壁面溫度和對流傳熱系數的平均相對偏差分別為0.85%和3.35%,從而驗證本文的數值計算模型是可靠的.

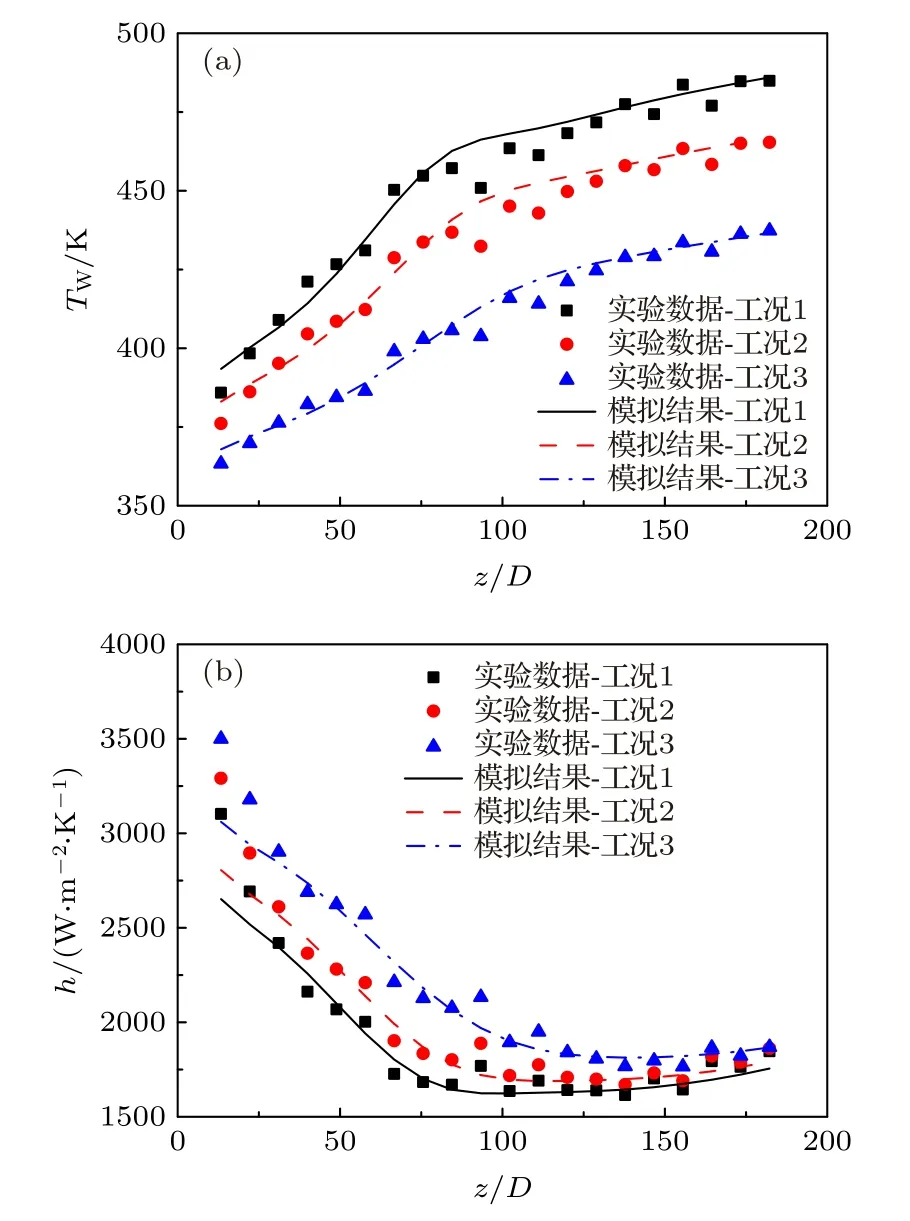
圖5 模型計算結果與文獻[16]實驗數據的對比 (a) 壁面溫度; (b) 對流傳熱系數; 其中,工況1,G = 868 kg·m–2·s–1,q = 231.0 kW·m–2,p = 9.22 MPa; 工況2,G = 873 kg·m–2·s–1,q = 216.2 kW·m–2,p = 9.09 MPa; 工況3,G = 874 kg·m–2·s–1,q = 191.8 kW·m–2,p = 8.71 MPaFig.5.Comparisons between numerical results and experimental data of Ref.[16]: (a) Wall temperature; (b) convective heat transfer coefficient.Case 1: G = 868 kg·m–2·s–1,q =231.0 kW·m–2,p = 9.22 MPa.Case 2: G = 873 kg·m–2·s–1,q =216.2 kW·m–2,p = 9.09 MPa.Case 3: G = 874 kg·m–2·s–1,q =191.8 kW·m–2,p = 8.71 MPa.

4 結果與分析

4.1 流體溫度和流動方向的影響

實際工程應用中,超臨界CO2在吸熱管內的流動方向存在多種情況,本文主要研究其在管內進行垂直向上、垂直向下和水平方向流動時的傳熱特性變化情況.圖6 為在G= 300 kg·m–2·s–1,q=500 kW·m–2和p= 7.5 MPa 的工況下,三種流動方向在高溫區對管內超臨界CO2傳熱特性的影響.可見,三種流動方向的對流傳熱系數均隨流體溫度的升高而近似線性的增大,其中垂直向下流動的對流傳熱系數最高,而垂直向上流動的對流傳熱系數最低,但它們的數值偏差不大,其絕對相對偏差小于0.68%.這是因為CO2的密度在高溫區會隨著流體溫度的升高而減小,在定質量流率 (G=ρu)下則使得流速增大,從而增強了湍流強度,導致對流傳熱系數隨流體溫度的升高而增大.另外,根據這三種極端流動方向對傳熱的影響結果,可推斷其他傾斜角度的流動方向對高溫區超臨界CO2吸熱管內傳熱特性的影響應該也不大.從圖6 還可得到Nu 數隨流體溫度的升高是減小的,與對流傳熱系數的趨勢相反,這是因為CO2的熱導率在高溫區是隨流體溫度的升高而增大的,從而說明在高溫區Nu 數受CO2熱導率的影響比對流傳熱更為明顯.

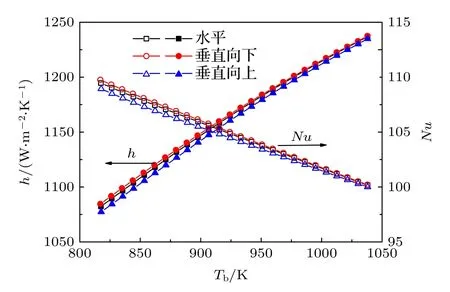
圖6 管內流體溫度和流動方向在高溫區對超臨界CO2傳熱特性的影響Fig.6.Effects of fluid temperature and flow direction on heat transfer of supercritical CO2 at high temperature region.

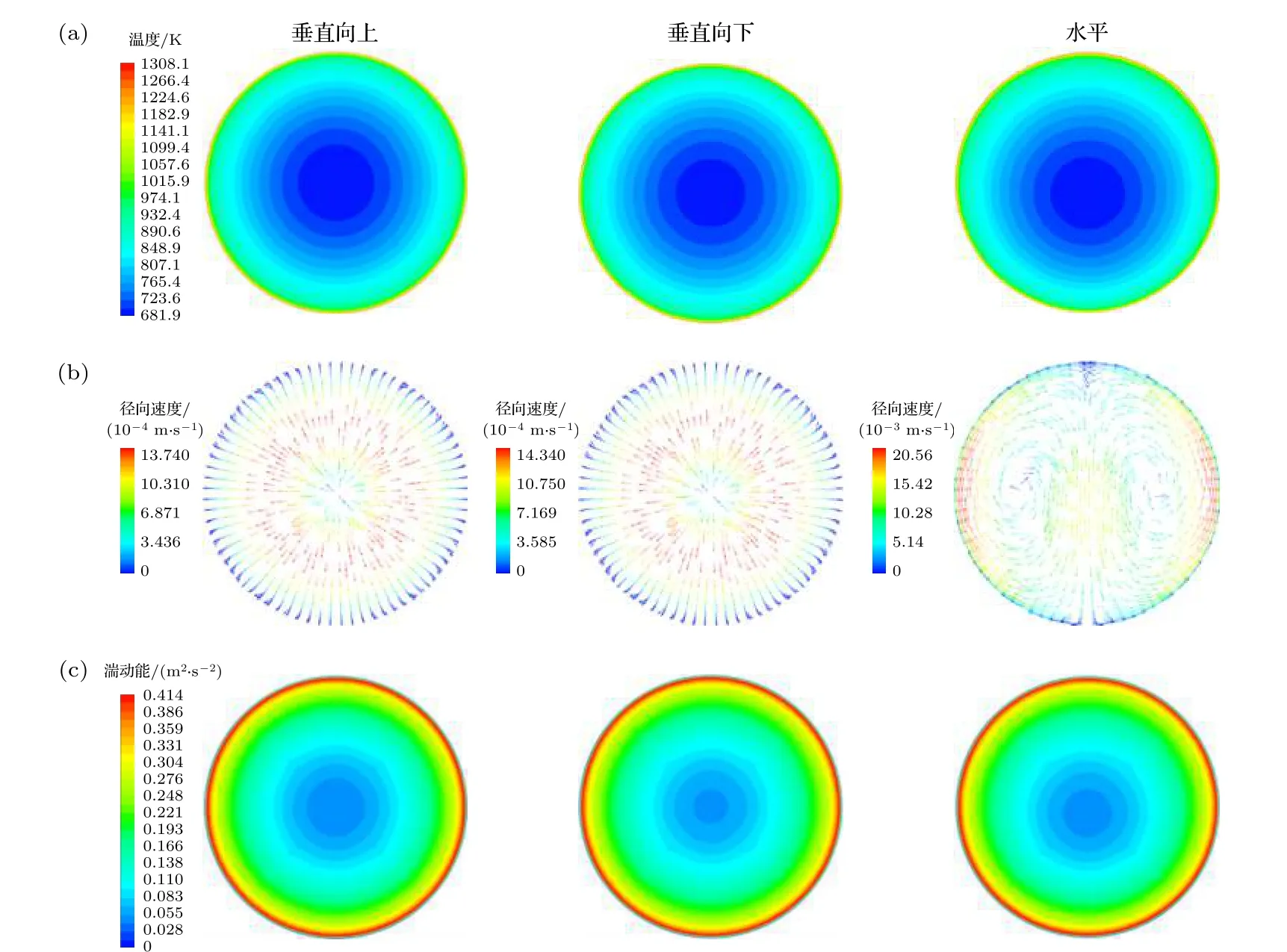
圖7 z = 250 mm 管截面平面上三種流動方向的流體 (a) 溫度云圖; (b) 徑向速度矢量圖; (c) 湍動能云圖Fig.7.(a) Temperature contours,(b) radial velocity fields,(c) turbulence kinetic energy contours on the plane of z = 250 mm for three flow directions.

圖7給出了在z = 250 mm 橫截面上的管內流體溫度和湍動能云圖以及徑向速度矢量圖.對于垂直向上和垂直向下流動,從圖7(a)可見,流體的溫度分布均呈徑向對稱,最低流體溫度位于管截面的中心,且向上流動的流體徑向溫度梯度略高于向下流動的流體徑向溫度梯度.從圖7(b)可見,垂直向上和垂直向下流動的流體徑向速度分布均呈現M 形.這是由于徑向溫度梯度的存在使得管截面流體產生徑向密度梯度,管中心流體由于溫度較低密度增大,導致其流速降低,而近壁面流體由于溫度較高密度減小,反而促使其流速增大,從而形成“M”形徑向速度分布.另外,對于吸熱管內向上流動,浮升力效應會降低邊界層剪切力,減弱湍流渦流的產生和擴散[17],從而削弱對流換熱.而對于向下流動,浮升力效應的影響則相反,所以向下流動的對流傳熱系數高于向上流動的對流傳熱系數.但從圖7(c)可見,它們的湍動能分布差別不大,所以它們的對流傳熱系數也偏差不大.而對于水平流動,從圖7(a)可見,其流體溫度分布并非呈徑向對稱,最低流體溫度位置是略微的向管底部偏移.從圖7(b)可見,在水平流動的流體徑向速度分布中,管截面兩邊的流體是沿管壁面向上運動,然后再沿管中心下降,從而在管截面兩邊形成二次渦流.而二次渦流的生成,使得最低流體溫度位置向管底部偏移.另外,水平流動的流體徑向速度比垂直向上和向下流動的徑向速度大一個數量級,且水平流動的管截面兩側流體徑向速度明顯高于其他管截面區域.從圖7(c)可見,雖然水平流動的流體徑向速度較高,但其湍動能反而比垂直向下流動略低.這可能是因為水平流動中剪切力大多用于加速管截面兩側流體速度,消耗了其湍動能.綜上所述,三種流動方向的湍流度和傳熱效率均相差不大.

4.2 系統壓力的影響

圖8 為在G = 300 kg·m–2·s–1,q = 500 kW·m–2和垂直向上流動的工況下,系統壓力在高溫區對管內超臨界CO2傳熱特性的影響.可見,系統壓力在高溫區對對流傳熱系數的影響極小,隨著系統壓力的增大,對流傳熱系數最多僅減小0.17%; 而Nu 數隨系統壓力的增大也僅有略微的減小,最大減小量為0.51%,且流體溫度越高系統壓力的影響越小.由圖2 可見: 在高溫區CO2的密度會隨著系統壓力的增大而增大,在定質量流率下,會使得流體流速減小,從而削弱傳熱; 但另一方面CO2的熱導率也會隨著系統壓力的增大而增大,從而強化傳熱.兩者綜合作用,使得對流傳熱系數的變化不大.然而,圖2 也顯示在高溫區系統壓力對CO2密度的影響明顯強于熱導率,但它們對對流傳熱系數的影響卻相當,說明在高溫區和本文所研究的系統壓力范圍 (7.5—9 MPa),CO2熱導率對其傳熱特性起著重要的作用,這也與4.1 節中Nu 數隨流體溫度增大而減小的原因一致.

圖8 系統壓力在高溫區對超臨界CO2 傳熱特性的影響Fig.8.Effect of pressure on heat transfer of supercritical CO2 at high temperature region.

4.3 質量流率的影響

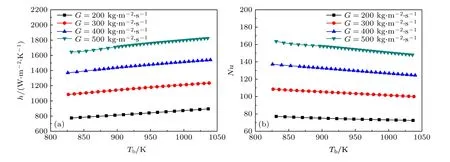
圖9 質量流率在高溫區對超臨界CO2 傳熱特性的影響Fig.9.Effects of mass flux on heat transfer of supercritical CO2 at high temperature region.

圖9為在p = 7.5 MPa,q = 500 kW·m–2和垂直向上流動的工況下,流體質量流率在高溫區對管內超臨界CO2傳熱特性的影響.可見,高溫區的對流傳熱系數和Nu 數均隨著質量流率的增大而明顯增大.這是因為質量流率越大,流體流速也越大,使得流體的湍流擴散速率增大,從而增強了對流換熱效應,導致對流傳熱系數增大.另外,管壁面邊界層厚度也會隨著流體流速增大而減小,導致熱阻變小,同樣強化了傳熱.

4.4 熱流密度的影響

圖10 為在G = 300 kg·m–2·s–1,p = 7.5 MPa和垂直向上流動的工況下,壁面熱流密度在高溫區對管內超臨界CO2傳熱特性的影響.可見,在高溫區隨著熱流密度的增大,對流傳熱系數和Nu 數均減小,且熱流密度越大其影響程度越明顯.由于隨著壁面熱流密度增大,近壁面的流體溫度會急劇升高,而流體溫度升高會造成其體積膨脹,引發流動加速效應[17].流動加速效應所形成的速度梯度方向與流動方向是相反的[18],這會導致近壁面處的湍流度減小.當近壁面處的低密度流體層達到足夠厚,會使得湍流邊界層轉化為層流邊界層,從而導致對流傳熱被削弱.

4.5 浮升力和流動加速效應的影響

根據現有文獻[19?22]可知,浮升力和流動加速效應在近臨界點溫區對管內超臨界CO2傳熱特性具有重要的作用.然而,目前不同文獻對兩種效應的定義各有不同,本文采用Liu 等[17]提出的判斷標準,分析在高溫區浮升力和流動加速效應對管內超臨界CO2傳熱特性的影響情況.本文所使用的浮升力因子 (Bu) 和流動加速因子 (Ac) 定義如下:

圖10 熱流密度在高溫區對超臨界CO2 傳熱特性的影響Fig.10.Effect of heat flux on heat transfer of supercritical CO2 at high temperature region.

式中,

Liu 等[17]指出當Bu< 1.3×10–5和Ac<3.3×10–6時,浮升力和流動加速效應對傳熱的影響小于3%,可以忽略不計.本文計算了不同工況條件下的Bu和Ac,如圖11 所示.如圖11(aI) 和圖11(aII) 所示,在高溫區隨著流體溫度的升高,Bu和Ac均減小,流動方向對它們幾乎沒有影響,這與流動方向對對流傳熱系數的影響規律一致(圖6).如圖11(bI) 和圖11(bII) 所示,隨著系統壓力增大,Bu會增大,而Ac幾乎不變.但所研究系統壓力范圍的Bu值均遠低于其閾值1.3×10–5,說明此時浮升力效應對傳熱的影響不大,因此即使Bu值隨著系統壓力的增大而增大,對流傳熱系數受系統壓力的影響仍很小 (圖8).如圖11(cI) 和圖11(cII) 所示,Bu和Ac均隨著質量流率的增大而減小,這是因為Re數會隨著質量流率的增大而增大,由 (11) 式和 (12) 式可見,Re數的增大會減小Bu和Ac.而對于垂直向上流動,浮升力和流動加速效應會惡化傳熱,Bu和Ac值的減小,使得流體流速增大強化傳熱的程度高于浮升力和流動加速效應惡化傳熱的程度,從而促使對流傳熱系數隨著質量流率的增大而增大 (圖9).如圖11(dI) 和圖11(dII) 所示,隨著熱流密度的增大,Bu和Ac均增大,這是因為壁面和流體的溫差會隨著熱流密度的增大而增大,使得管內流體密度梯度增大,從而導致浮升力和流動加速效應增強,削弱了對流傳熱,這與熱流密度對對流傳熱系數的影響一致 (圖10).

圖12 為在本文所研究的工況條件下,Bu和Ac的分布圖.可見,所有工況的Bu值均遠低于其閾值1.3×10–5,而除了最低熱流密度工況 (G=300 kg·m–2·s–1,q= 100 kW·m–2,p= 7.5 MPa和垂直向上流動) 外,其余工況的Ac值均高于其閾值3.3×10–6.說明在本文所研究的工況條件(高溫高熱流密度) 下可忽略浮升力對傳熱的影響,而由高熱流密度引起的流動加速效應會明顯惡化傳熱.

4.6 與現有文獻傳熱關聯式計算結果的對比

現有文獻中關于管內超臨界CO2的傳熱關聯式大多是基于近臨界點溫區的傳熱數據提出的,其對高溫區傳熱數據的預測還有待評估.表2 為目前常用的八種管內超臨界流體傳熱關聯式,其可分為基于熱物性修正和基于無量綱數修正兩種類型.將關聯式計算結果與模擬結果進行對比,并采用平均絕對相對偏差 (mean absolute relative deviation,MARD) 和平均相對偏差在±20%以內的數據點占總數據量的比例 (η) 作為關聯式預測能力的評估標準,MARD 具體定義如下:

圖11 (a) 流動方向、(b) 系統壓力、(c) 質量流率、(d) 熱流密度在高溫區對 (I) Bu 和 (II) Ac 的影響Fig.11.Effects of (a) flow direction,(b) pressure,(c) mass flux,(d) heat flux on (I) Bu and (II) Ac at high temperature region.

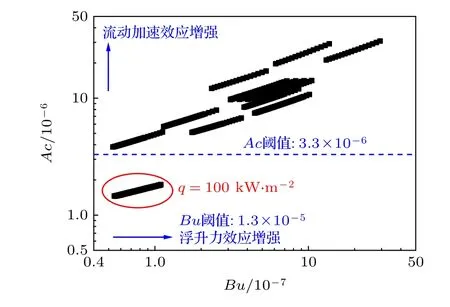
圖12 Bu 和Ac 的分布圖Fig.12.Distributions of Bu and Ac .

式中Nucal,Nunum為傳熱關聯式計算、模擬結果.

圖13 為其中預測效果較好的五種關聯式計算結果與模擬數據對比的散點圖.從表2 和圖13 可得,基于熱物性修正的傳熱關聯式對本文高溫區數據預測的結果優于基于無量綱數修正的關聯式得到的結果,且模擬數據均大于計算結果.由前面的分析可得,高溫區的浮升力效應對傳熱的影響可忽略,而雖然流動加速效應對傳熱有一定的影響,但Nu數受導熱傳熱的影響比對流傳熱的影響要大,因此高溫區的管內超臨界CO2傳熱數據的預測使用基于熱物性修正的傳熱關聯式更合適.其中,Krasnoshchekov 和Protopopov[24]的關聯式對本文傳熱數據預測效果最好,其平均絕對相對偏差為8.1%,且100%的數據點在±20%的平均相對偏差范圍內.

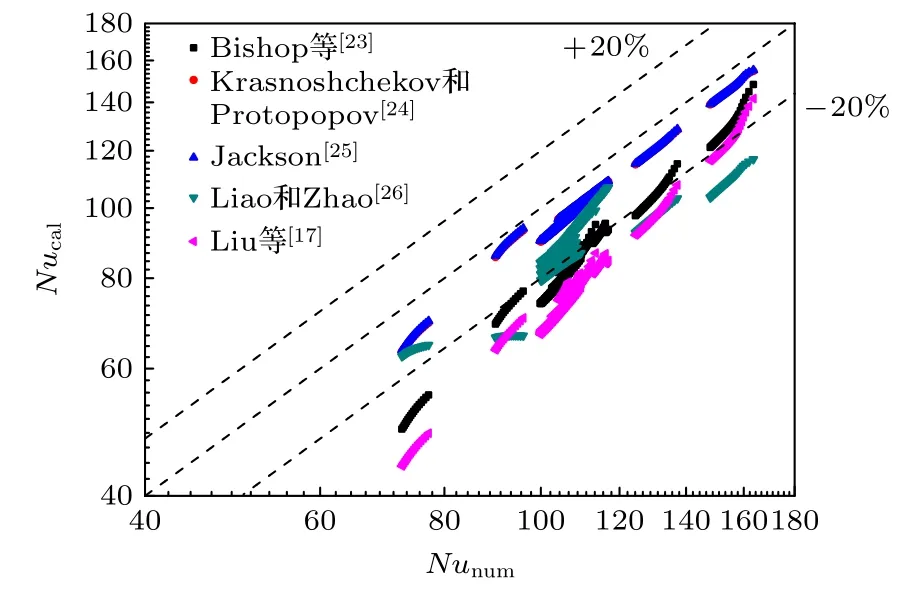
圖13 傳熱關聯式計算結果與模擬數據的對比Fig.13.Comparisons of the calculated heat transfer results by the correlations with the numerical results.

表2 傳熱關聯式計算結果與模擬數據的對比Table 2.Comparisons of the calculated heat transfer results by the correlations with the numerical results.

表2 （續） 傳熱關聯式計算結果與模擬數據的對比Table 2 (continued).Comparisons of the calculated heat transfer results by the correlations with the numerical results.

5 結 論

本文對超臨界CO2在高溫吸熱管內的傳熱特性進行了數值模擬研究,分析了流體溫度、流動方向、系統壓力、質量流率和熱流密度對對流傳熱系數和Nu數的影響,揭示了不同工況條件下的傳熱機理,探究了浮升力和流動加速效應在高溫區對傳熱的影響情況,并選取了八種常用的管內超臨界流體傳熱關聯式與模擬結果進行了對比,主要得到以下結論:

1) 在高溫區 (800—1050 K),隨著流體溫度的升高,對流傳熱系數近似線性的增大,而Nu數近似線性的減小;

2) 垂直向上、垂直向下和水平三種流動方向以及系統壓力對高溫區的對流傳熱系數和Nu數影響均很小;

3) 高溫區的對流傳熱系數和Nu數均隨著質量流率的增大和熱流密度的減小而明顯的增大,且熱流密度越大其影響程度越明顯;

4) 在本文所研究的工況范圍內,浮升力效應對傳熱的影響可忽略,而由高熱流密度引起的流動加速效應會明顯惡化傳熱;

5) 高溫區的管內超臨界CO2傳熱數據的預測使用基于熱物性修正的傳熱關聯式優于基于無量綱數修正的關聯式,且Krasnoshchekov 和Protopopov[24]的關聯式預測效果較優,對模擬結果預測的平均絕對相對偏差為8.1%.