矢量疊加初至波定位方法及精度評價

楊海申 徐麗軍 馬 潔 侯昆鵬 肖永新

(東方地球物理公司采集技術中心，河北涿州 072751)

0 引言

在海上勘探中，無論是OBC還是OBN勘探，檢波器都是通過拋擲或機械方式放置于海底，電纜或節點檢波器在到達海底過程中因受海流[1]、潮汐[2]、船速以及檢波器沉降速度的影響而偏離設計位置。而實時導航提供的測量資料只是檢波器離開放纜船到達海面的位置(一次定位點)信息，檢波器在海底的實際位置與導航結果存在一定偏差，因此必須通過某種方法得到檢波器在海底的實際位置[3]。厘清檢波器在海底的準確位置，能提高后期資料處理和解釋的可信度[4]，二次定位技術正是在這種需求下應運而生的。對檢波點進行二次定位的現行主要方法是聲波定位法和初至波定位法[5]。

聲波定位方法需專用聲學檢波器接收由聲波發生器發出的聲學信號，然后利用圓圓定位原理進行定位[6-10]，其特點是需用專項設備和專用施工流程，采集費用高，施工效率低，在淺水域數據采收率低，最大接收距離通常小于1000m，但其計算精度高，在前期海上勘探中應用較多。

初至波定位方法則是利用地震記錄初至時間進行定位[11]，不需專用聲納設備及施工流程，利用常規采集地震數據，通過拾取的初至計算檢波點位置[12]。與聲波定位相比，采集費用低、定位效率高，應用更為普及。經過多年發展，初至波定位方法衍生出多種方法，定位精度也在逐步提高[13-14]。按初至波定位方法的原理可分為初至波圓圓二次定位法[7，15-16]、折射波二次定位法[17-18]、網格掃描定位法[19]、直達波折射波二次定位法[20-21]和掃描擬合定位方法等五種。但各種方法又有其自身特點和限制，如初至波圓圓定位法計算效率較低，折射波法適用于折射波發育、有穩定折射層的探區，網格掃描法的定位范圍受網格范圍限制等[7，15-21]。

本文在充分調研上述諸多算法基礎上，提出一種新的初至波定位法——矢量疊加方法。該方法通過構建每個炮檢對的位置矢量，并進行矢量疊加，得到檢波點的準確坐標位置，并給出定位精度的量化評價指標，形成了一套從初至拾取、定位計算到定位精度評價的完整的高精度定位方法。

1 矢量疊加定位方法原理

假設某檢波點初始坐標為(x0，y0，z0)，已知第i個炮點的坐標為(xi，yi，zi)，則檢波點到炮點的理論炮檢距為

(1)

此時該檢波點的初至時間為ti，海水速度為v，則傳播路程(即實際炮檢距)為

Wi=vti

(2)

定義向量Di，其模為實際炮檢距Wi減去理論炮檢距Ri的差的絕對值|Wi-Ri|。若Wi-Ri大于零，則向量方向從炮點指向檢波點； 若Wi-Ri小于零，則向量方向從檢波點指向炮點。

將第i個炮檢對的矢量記為Di，則每個炮點都可形成一個向量，稱為殘差向量，如圖1所示。

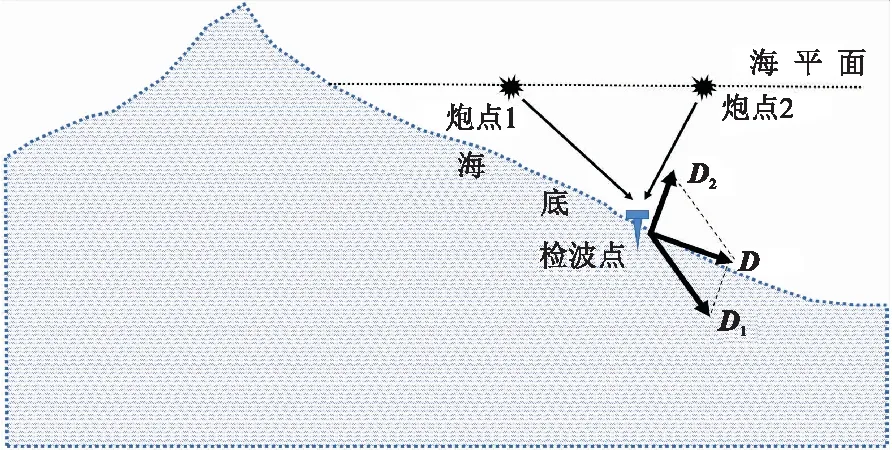
圖1 矢量疊加原理示意圖

對檢波點與每個炮點的殘差向量Di求和，得到總矢量D。檢波點按矢量移到新位置，得到初至波定位新坐標，總矢量方向和即為檢波點移動方向，總矢量大小就是檢波點移動距離。顯然有

(3)

式中n為與該檢波點對應的炮點數。

在實現過程中，需進行多次迭代計算，檢波點逐步逼近準確位置。圖2顯示某檢波點迭代收斂過程，可見經10次迭代后，收斂誤差達到0.1m。實際的初至數據、速度及炮點坐標都會有誤差，定位精度也受其一定影響。利用理論數據計算，該方法定位精度可達毫米級以內。

圖2 矢量疊加迭代收斂曲線

嚴格地說，矢量疊加定位法也屬于圓圓定位法的一種，只是實現方式不同。一般要求前提條件是至少有三個炮點，且處于不同方位。若炮點位于同一直線或集中于一個方位，對應的矢量圖也會集中于一個方向，雖能快速收斂，但可能會造成在其他方位定位坐標不準確，從而導致整體定位精度降低。對于三維勘探，一般都能滿足此條件。通過構建不同方位的殘差向量，再根據矢量和定位檢波點位置(圖3)。

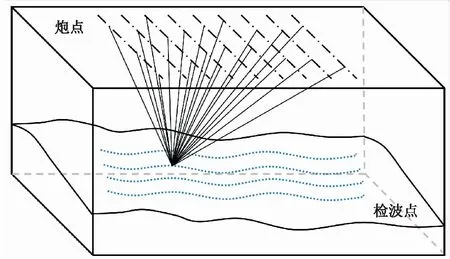
圖3 三維勘探炮點分布示意圖

該定位方法能適應空間上的變化，即對x、y、z三個方向的坐標進行定位。基于現行施工方式，氣槍激發位置大體處于同一深度面，導致對z坐標的定位欠準確。為彌補此缺憾，可按定位后的(x，y)坐標，從海底面高程中得到新的z坐標。

2 速度的計算

定位計算需首先求取初至波速度。在較深海域，初至波即是沿海水傳播的直達波(圖4b)。但對于淺海區域，較大炮檢距的初至波往往是來自海底的透射波或折射波。隨著炮檢距增大，初至波速度逐漸增高，初至—炮檢距關系表現為曲線(圖4a)。

圖4中的橫坐標炮檢距由炮點和檢波點坐標計算得到，縱坐標為經線性動校正(LMO)后的初至時間。對初至點進行曲線最小二乘擬合，曲線斜率的倒數即是初至波的速度。具體實現中，將炮檢距分為若干段，計算每一段的平均速度，得到隨炮檢距變化的速度場。由于檢波點坐標位置存在偏差，得到的初始速度也是有誤差的。在矢量疊加迭代過程中，隨著檢波點坐標位置的修正，速度也需重新計算和更新，這樣才能保證最終定位精度。

圖4 淺海(a)和深海(b)區域的初至分布

在本文方法實現中，對多個檢波點的初至同時進行擬合，以保證足夠數據量及速度值的穩定。另外，應選擇近炮檢距范圍(0～500m)參與計算，避免出現隨炮檢距的變化速度產生較大變化。

3 坐標初始值對定位的影響

為考察定位方法的穩定性及對初始坐標的依賴性，選擇M海域節點實際資料，給定偏離20m后不同位置初始坐標做定位計算。經測試，定位后坐標都能收斂到一個固定值(表1、圖5)。分析定位后坐標(圖6)，其最大位置差僅約為0.15m，可認為不同初始坐標對定位結果的影響為±0.075m。對于現行勘探精度要求，此偏差可忽略不計。

表1 不同初始坐標的定位結果 單位：m

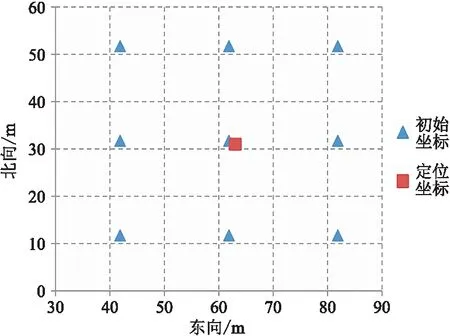
圖5 初始坐標與定位后坐標平面分布圖

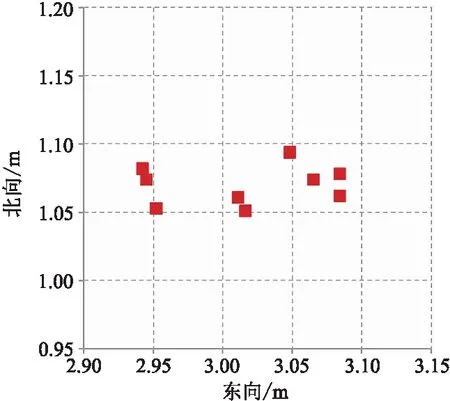
圖6 不同初始坐標的定位計算結果平面分布

4 定位精度的評價

對定位精度的評價有三種常用方式。一是對道集進行LMO，觀察初至是否“拉平”，是一種定性評價方式。LMO與使用的速度有關，當初至速度隨炮檢距變化時，準確的速度不易給定； 而且“拉平”效果也是定性的，無量化指標。二是查看異常值是否過多，整體偏差性趨勢是否明顯[22]，這也是一種定性評價方式。三是與聲波定位對比。一般認為聲波定位結果是準確可靠的，若初至波定位結果接近聲波定位結果，就可認為該初至波定位結果是準確的。此方式須有專用設備和額外的施工流程，不易推廣。

本文提出兩種定位精度量化評價方法，可計算三種量化屬性，用于對定位精度進行量化評價。另外，殘差向量分布、初至分布等圖件，也可定性地評判檢波點坐標位置精度。

4.1 疊加能量

以正確炮檢點位置和合適速度進行LMO，初至可被拉平。對于校正后道集，在初至附近選擇一個時窗，對時窗內道集進行同向疊加，可得到最大能量值。若檢波點位置不正確，LMO后道集不能被拉平，此時疊加能量小于最大值。因此，根據疊加能量，可判別道集的拉平程度。但疊加不僅能反映檢波點位置的偏差，也與LMO速度有關。當采用有偏差的速度時，LMO后的道集會呈周期性對稱起伏變化(圖7a)，其對應的疊加能量也不能達到最大值。從實際檢波點道集LMO后疊加能量的對比(圖7)可以看出，LMO速度若有誤差，對同一炮檢距道的影響是一樣的，即相同炮檢距道的LMO校正量一致。

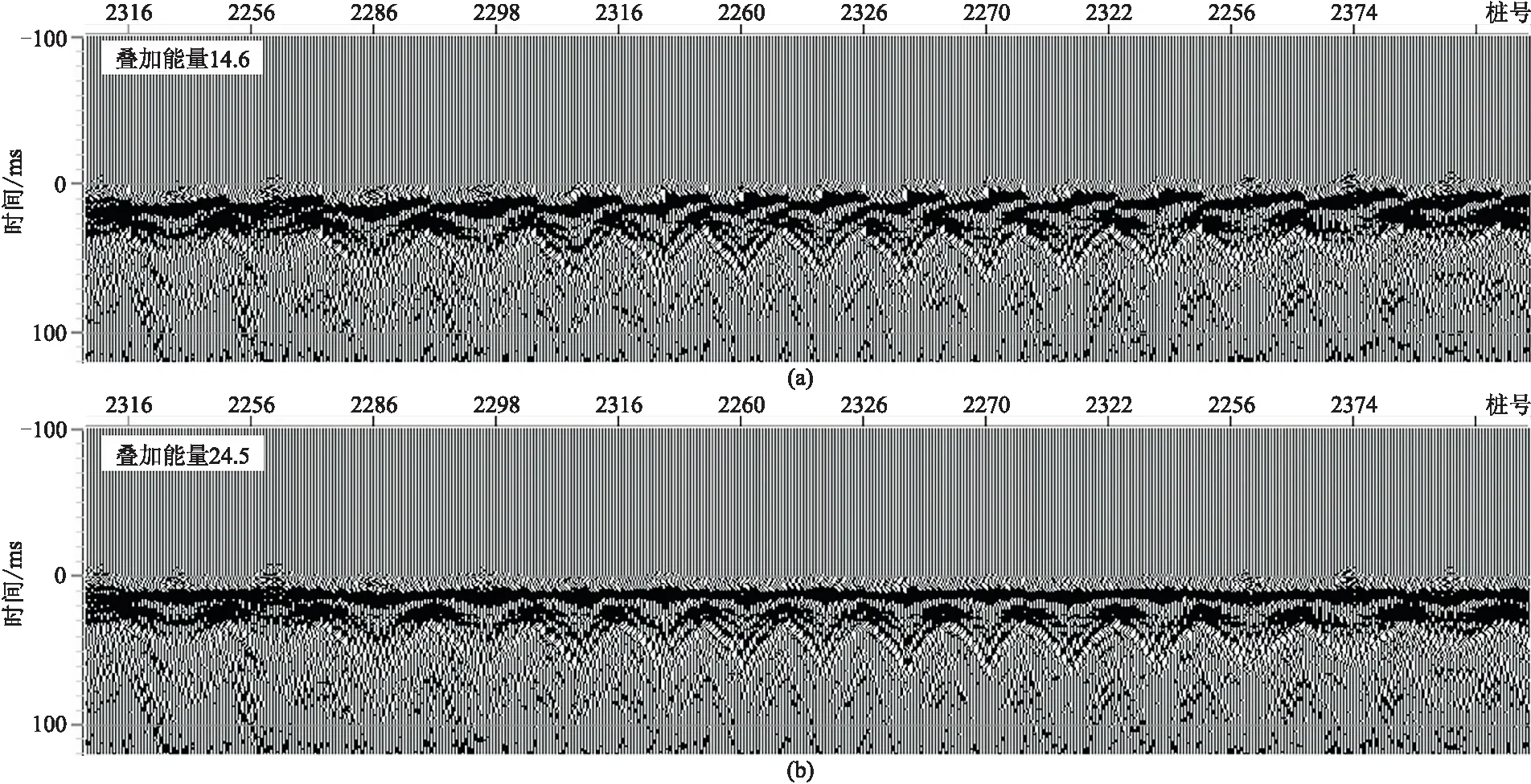
圖7 LMO后檢波點坐標存在偏離(a)與處于正確位置(b)的道集對比

根據此原理，提出按炮檢距分段疊加方法： 將炮檢距分成若干段，在每段內炮檢距接近，LMO后能同相疊加； 然后將各個炮檢距段的能量再疊加，得到總能量，這樣就避免了由LMO速度偏差造成的疊加能量減小，即疊加能量只與檢波點位置有關。

檢波點位置偏差與疊加能量并非單調線性關系，隨位置的偏差會出現多個極值，但在準確位置附近(如±5m范圍)會有一個極大值(圖8)。因此，根據疊加能量可以有效判別檢波點位置的準確程度，尤其是細微的坐標差別，但無法直觀評判哪個位置的LMO可使道集排列更平直，此時可通過疊加能量定量判別哪個坐標位置更準確。

圖8 疊加能量變化曲線

4.2 殘差向量分布

對于實際資料，由于各種誤差的存在，即使檢波點坐標位置正確，殘差向量仍不會為零。將檢波點定為殘差向量的起點，并將該點設為中心點，每一條線代表一個炮點的殘差向量，繪制出各個殘差向量分布圖(圖9)； 再根據該分布圖統計出兩種屬性，判別坐標位置的精度。

圖9 殘差向量分布示意圖

屬性一為殘差向量和(δ)。所有殘差向量矢量和的模為∣D∣，該值越小，定位精度越高。由于本文初至波定位法即是依據矢量和，所以初至波定位后的殘差向量和幾乎趨于零。但不同定位方法的該屬性值不同，對于正確的初至時間，精度高的檢波點坐標總是對應小的殘差向量和。

屬性二為離散度，是殘差向量模的均方根φ。φ越小表明定位精度越高，其表達式為

(4)

圖10a所示的一次定位坐標分布圖中離散度為4.37，經初至波定位后(圖10b)的離散度(φ)降為1.84；而殘差向量和(δ)屬性，由一次定位坐標的5.539驟減為初至波定位后的0.002，趨近于零，顯然初至波定位后坐標位置更準確。檢波點定位前、后坐標的距離是5.50m。因此，小離散度檢波點位置更居中(矢量中心)，大離散度檢波點位置偏離矢量中心，偏離中心點的方位基本可確定檢波點坐標偏離的距離和方向。

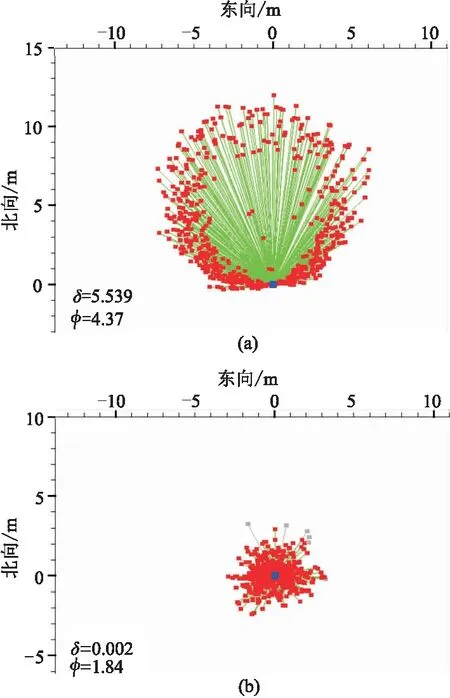
圖10 實際檢波點資料的殘差向量分布圖(a)一次定位坐標； (b)初至波定位坐標

4.3 初至分布

從不同炮檢距的LMO后初至時間分布也可直觀看出檢波點坐標位置的定位精度。對比一次定位與初至波定位可看出，后者的初至點分布(圖11b)明顯變得收斂和集中了，表明初至波定位后的坐標更準確。檢波點定位前、后坐標的距離是3.65m。

圖11 一次定位(a)和初至波定位(b)坐標分布圖

5 定位方法對比及定位條件分析

矢量疊加初至波定位方法在中國大港淺海區及南海某區、菲律賓海域等地區進行了測試驗證，定位精度均能達到3m以內。圖12為M海域施工的炮檢點平面圖，定位計算所用炮檢距范圍是0～800m，初始坐標為(已做過常規二次定位的)成果坐標，經初至波定位后，與原坐標差都在3m以內，箭頭指向坐標差最大檢波點。從殘差向量分布(圖13)可見初至波定位前、后離散度分別為3.20和2.40。初至波定位后離散度變小，檢波點更居中，計算結果精度高于原成果坐標，驗證了該方法的有效性。

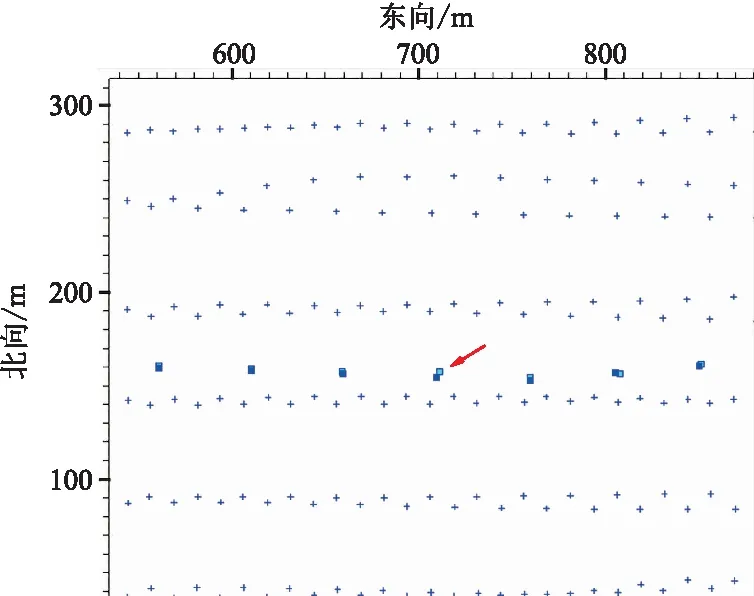
圖12 M海域炮檢點位置平面圖

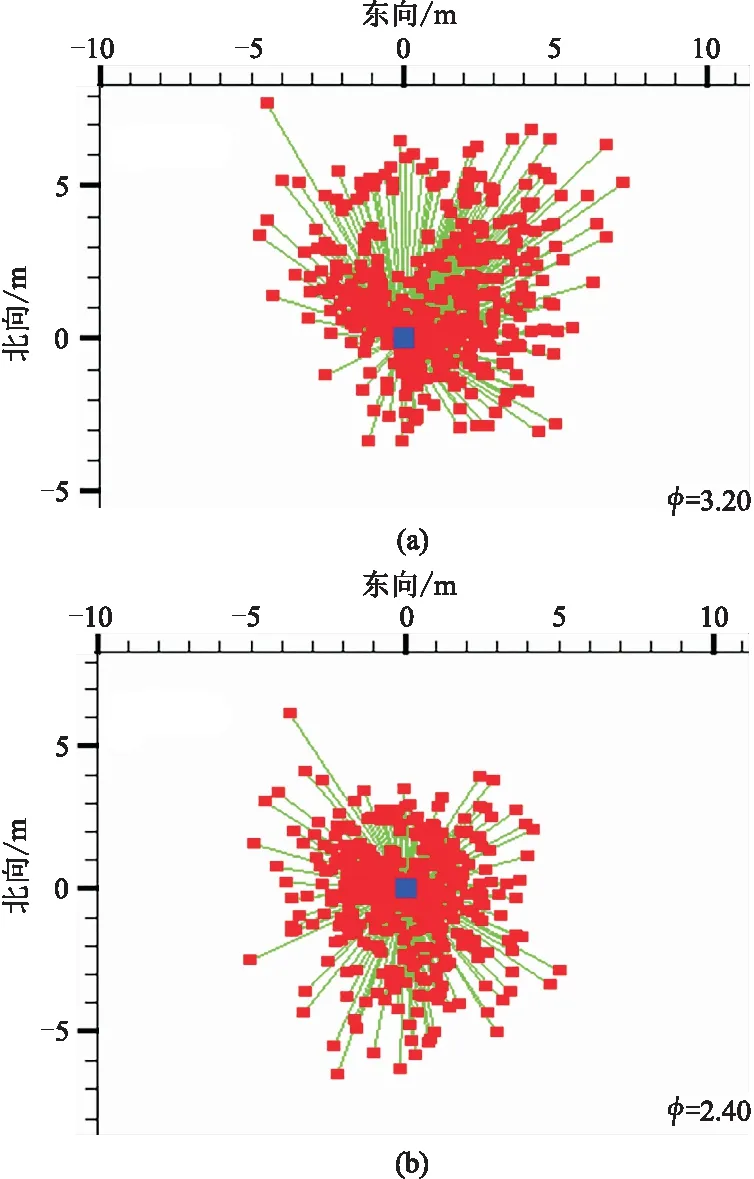
圖13 M海域定位前(a)、后(b)向量分布圖

進一步分析得知，除聲納定位本身誤差外，時效性是聲納定位的一個弱項，聲納定位時間與氣槍放炮時間存在幾小時甚至一二天的時間差，在這期間檢波點的飄移是造成位置偏差的主要原因。

實際應用中也發現該定位及評價方法的適用范圍。當炮點位置的分布不均勻或只有遠炮檢距炮點等情況下，可能會造成較大的定位誤差，定位精度評價也會失效，因此需首先根據資料情況確定是否滿足適用條件。

圖14在海外N地區的炮檢點位置平面圖，炮檢距范圍是2000～4000m，無近炮檢距資料，且檢波線位于炮點一側。圖15為圖14中箭頭所指檢波點的初至波定位結果與聲納定位結果的對比，經過LMO后，雖然初至波定位能將道集拉得更平，但通過與聲納所定位置的對比，兩者相差22m。雖然從疊加能量、離散度等分析，初至波定位結果的精度更高，但通過各種資料證實，聲納坐標位置是正確的。

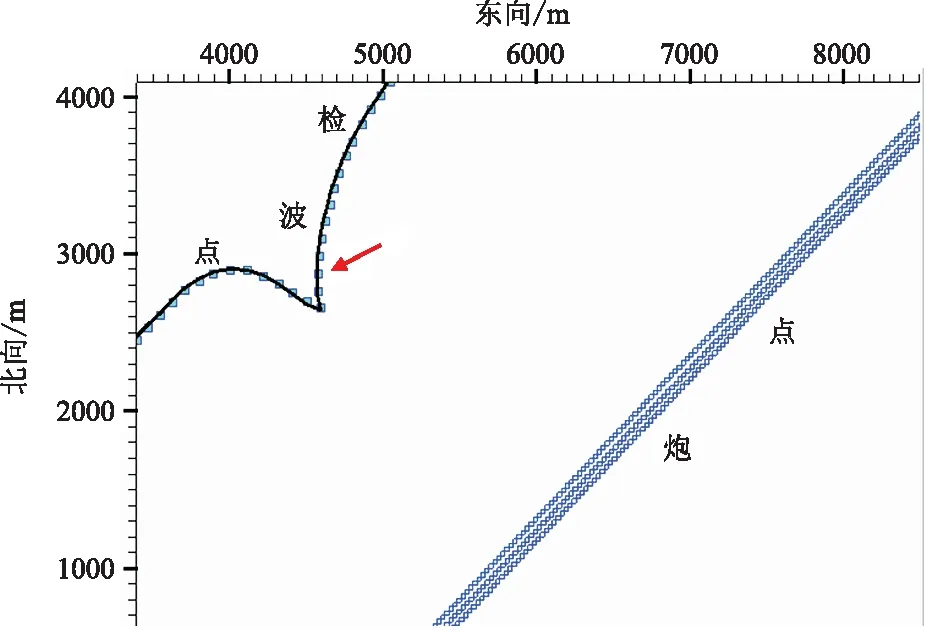
圖14 N地區炮檢點位置平面圖

圖15 N地區聲納定位(a)與初至波定位(b)LMO對比

分析其原因，一是隨著炮檢距增大各種誤差也隨之增大，二是炮點只是分布在檢波點一側，缺少其他方位的炮點，導致定位誤差急劇增大。因此，應先判定本方法的適用條件，無條件的使用會造成錯誤的結果。

6 結束語

本文提出矢量疊加初至波定位方法，該方法計算簡單、效率高，每個檢波點定位計算時間只需約5ms； 同時，提出了疊加能量、殘差向量矢量和、離散度等屬性，為檢波點二次定位精度的評價提供了量化指標； 另外，殘差向量分布、初至分布等圖件，也反映了檢波點的定位精度。

通過實際資料的對比，絕對定位誤差小于3m，大部分節點定位誤差甚至小于1m，完全滿足常規施工的要求。該定位方法及精度評價方法現已形成一套完整的克浪軟件產品，在印尼海上勘探Tangguh OBN項目的212萬炮數據采集中，所有節點均采用了初至波定位計算，除個別節點外，絕大多數的節點定位精度高于或等同聲納定位結果。隨著該方法的推廣，將會在更多的項目中發揮其應有的作用。

中國石油集團東方地球物理公司海洋物探處全海燕、徐朝紅、杜海濤、韋秀波、劉昭、丁冠東、劉磊等，采集技術中心王建峰、齊英赫等，為本文方法的研究提供了重要的幫助與指導，在此表示衷心感謝。