種群具有離散Leslie年齡結(jié)構(gòu)的動(dòng)力學(xué)優(yōu)化算法
黃光球,陸秋琴
西安建筑科技大學(xué)管理學(xué)院,西安 710055
群智能優(yōu)化算法[1]是啟發(fā)式算法的一種,其基本求解策略不依賴優(yōu)化問題的特征(如梯度、多次可微性等),而是依賴于試探解之間的信息交換能力。群智能優(yōu)化算法之所以采取此策略,是因?yàn)閮?yōu)化問題在很多情況下無法求得其梯度或者不具備任何可微性。為了使得試探解之間的信息交換具有合理性,群智能優(yōu)化算法經(jīng)常依據(jù)一些特殊的自然現(xiàn)象構(gòu)造而得。因此,一種自然現(xiàn)象的質(zhì)量?jī)?yōu)劣對(duì)群智能優(yōu)化算法的性能影響重大。
目前,具有代表性的新一代群智能算法有烏鴉算法[2]、海洋掠食者算法[3]、完全遷徙型生物地理學(xué)算法[4]、人工藻類算法[5]、磷蝦群算法[6]、鯨魚算法[7]、雜交蜂群算法[8]、反向?qū)W習(xí)粒子群算法[9]、花授粉算法[10]等。這些算法均來自一些特殊的自然現(xiàn)象,但這些自然現(xiàn)象有一個(gè)共同的缺陷就是無法用數(shù)學(xué)模型進(jìn)行描述。因此,基于這些自然現(xiàn)象所構(gòu)造出來的算法的性能設(shè)計(jì)無法奠定在堅(jiān)實(shí)的數(shù)學(xué)分析基礎(chǔ)之上,該缺陷也是傳統(tǒng)群智能算法的缺陷。此外,因這些算法沒有數(shù)學(xué)模型基礎(chǔ),故相關(guān)參數(shù)選擇也相當(dāng)困難。于是,若一個(gè)自然現(xiàn)象能夠被數(shù)學(xué)模型恰當(dāng)描述,基于該自然現(xiàn)象的群智能算法就可以克服上述缺陷。
一個(gè)自然現(xiàn)象能否成為構(gòu)造一個(gè)群智能優(yōu)化算法的生物活動(dòng)場(chǎng)景,必須包含有兩個(gè)條件:一是生物個(gè)體不斷進(jìn)化,符合“適者生存,優(yōu)勝劣汰”的自然規(guī)律;二是生物個(gè)體之間存在相互作用關(guān)系。第一個(gè)條件用來構(gòu)造算法的邏輯結(jié)構(gòu)并確保該算法具有全局收斂特征,第二個(gè)條件用來構(gòu)造算子,個(gè)體類型越多,個(gè)體之間相互作用關(guān)系越豐富,所能構(gòu)造出來的算子也就越多,算子的性能也越強(qiáng)。此外,若該自然現(xiàn)象還能被數(shù)學(xué)模型恰當(dāng)描述,則據(jù)此所構(gòu)造出來的群智能優(yōu)化算法的性能分析和參數(shù)選擇將具有很好的科學(xué)依據(jù)[11]。
由具有不同性別、不同年齡的生物個(gè)體所組成的生物種群在一個(gè)生態(tài)環(huán)境中生存進(jìn)化,是一種很常見的自然現(xiàn)象[3],該現(xiàn)象就滿足構(gòu)造一個(gè)群智能優(yōu)化算法的兩個(gè)條件。不僅如此,該自然現(xiàn)象既能被數(shù)學(xué)模型很好描述,又能提供高度多樣化的個(gè)體間相互作用關(guān)系。本文正是依據(jù)該自然現(xiàn)象提出了一種新的群智能算法,即種群具有離散Leslie 年齡結(jié)構(gòu)的動(dòng)力學(xué)優(yōu)化算法,簡(jiǎn)稱PDO-DLAS(population dynamic optimization algorithm with discrete Leslie age structure)算法,該種群動(dòng)力學(xué)模型簡(jiǎn)稱為L(zhǎng)eslie模型[12]。Leslie 模型具有較好的應(yīng)用價(jià)值,已得到較好的研究,目前研究進(jìn)展如下:
(1)種群特征分析[13-18]。在該方面,通過構(gòu)建Leslie模型,研究種群的特征,如擴(kuò)散特征、穩(wěn)定性特征、持久和湮滅特征等。
(2)種群控制研究[19-22]。在該方面,通過構(gòu)建Leslie控制模型,研究種群規(guī)模的最優(yōu)控制或收獲問題。
PDO-DLAS 算法依賴于Leslie 模型,因此上述模型的研究可為PDO-DLAS 算法的構(gòu)造奠定良好的理論基礎(chǔ)。與文獻(xiàn)[2-10]描述的算法相比,該算法具有如下特點(diǎn):
(1)Leslie 年齡結(jié)構(gòu)使得個(gè)體自動(dòng)依據(jù)年齡分成多個(gè)類別,可大幅提升個(gè)體的多樣性,從而降低個(gè)體陷入局部陷阱的概率。
(2)算法參數(shù)的選擇依據(jù)Leslie 數(shù)學(xué)模型確定,因而具有堅(jiān)實(shí)的理論依據(jù)。
(3)依據(jù)Leslie 模型描述的生態(tài)場(chǎng)景設(shè)計(jì)出來的算子具有充分的理論依據(jù)。
(4)個(gè)體進(jìn)化滿足達(dá)爾文進(jìn)化論規(guī)律,既可確保算法具有全局收斂性,又可使得個(gè)體進(jìn)化每次只涉及極少特征的改變,可大幅提升計(jì)算速度。
由于PDO-DLAS 算法具有獨(dú)特的優(yōu)勢(shì),對(duì)其進(jìn)行研究很有意義。
1 PDO-DLAS 算法構(gòu)建原理
考慮一類優(yōu)化問題:

式中,Rn是n維歐氏空間,n為優(yōu)化問題的維數(shù);X=(x1,x2,…,xn)是一個(gè)n維解向量;f(X)為目標(biāo)函數(shù);H為搜索空間。
1.1 決策變量與生物個(gè)體的對(duì)應(yīng)關(guān)系
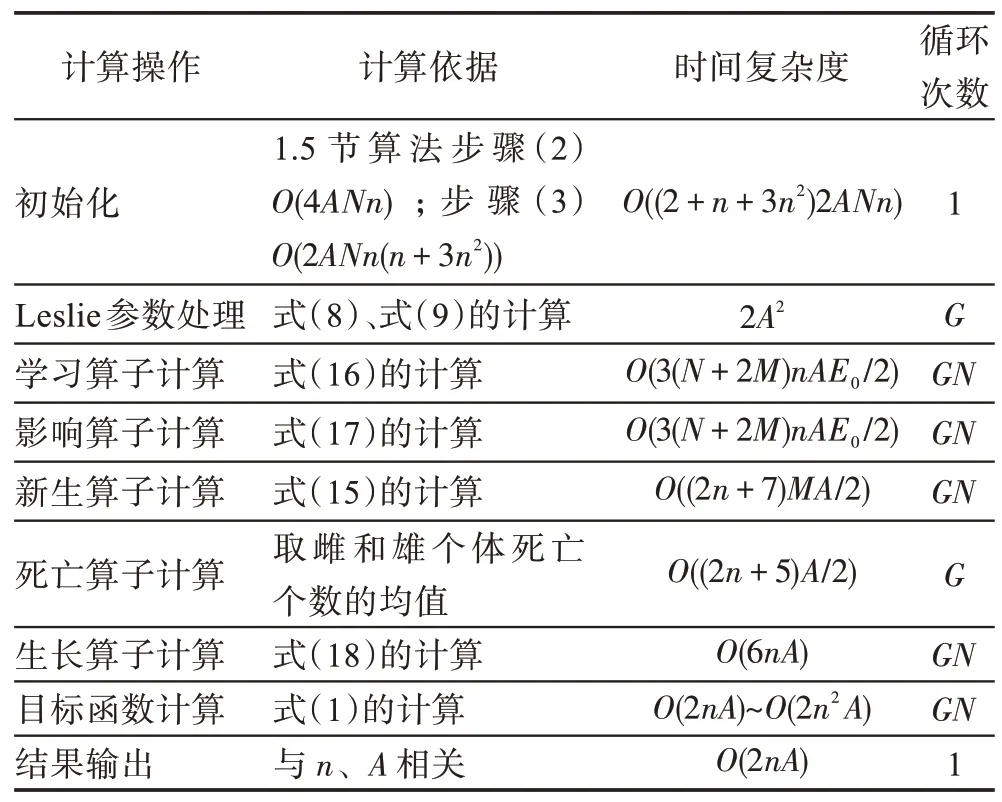
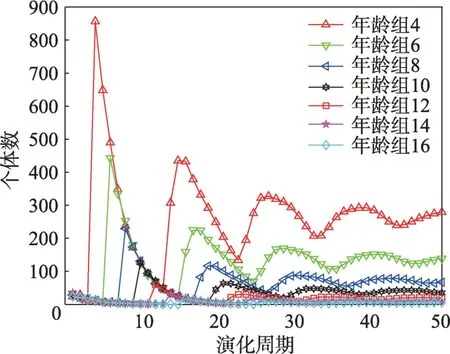
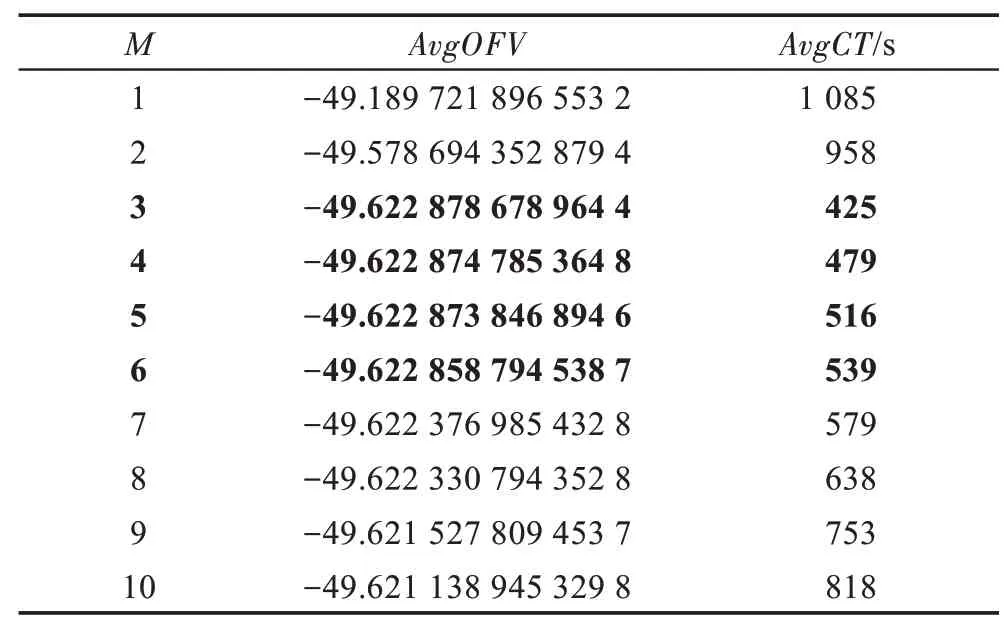
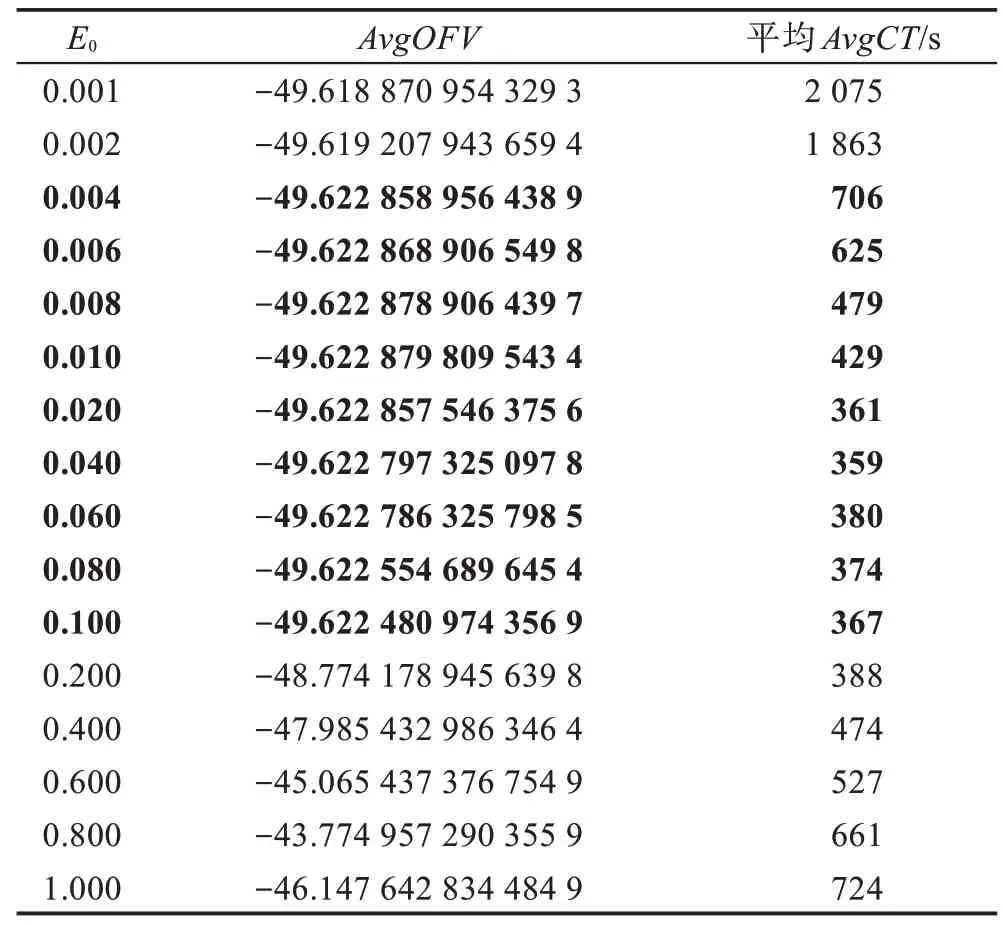
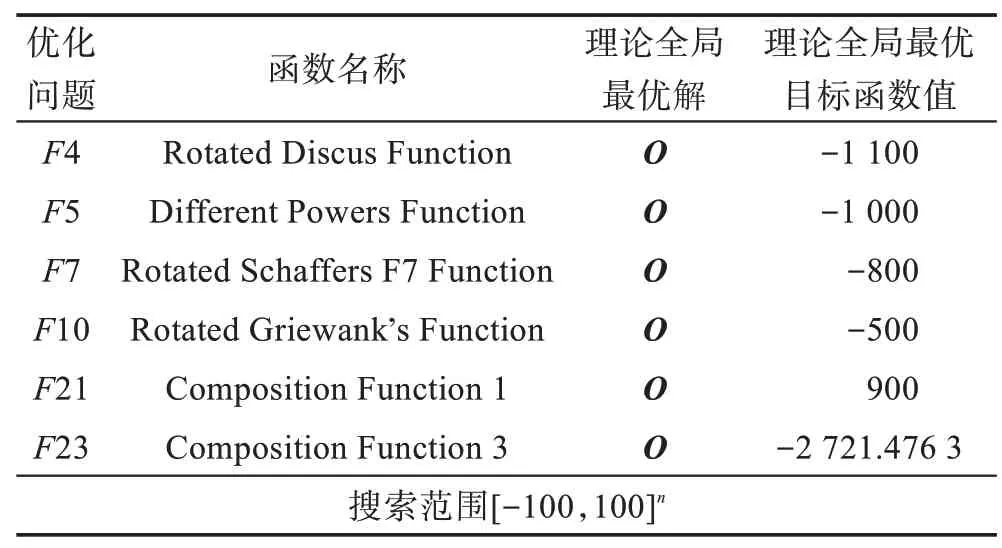
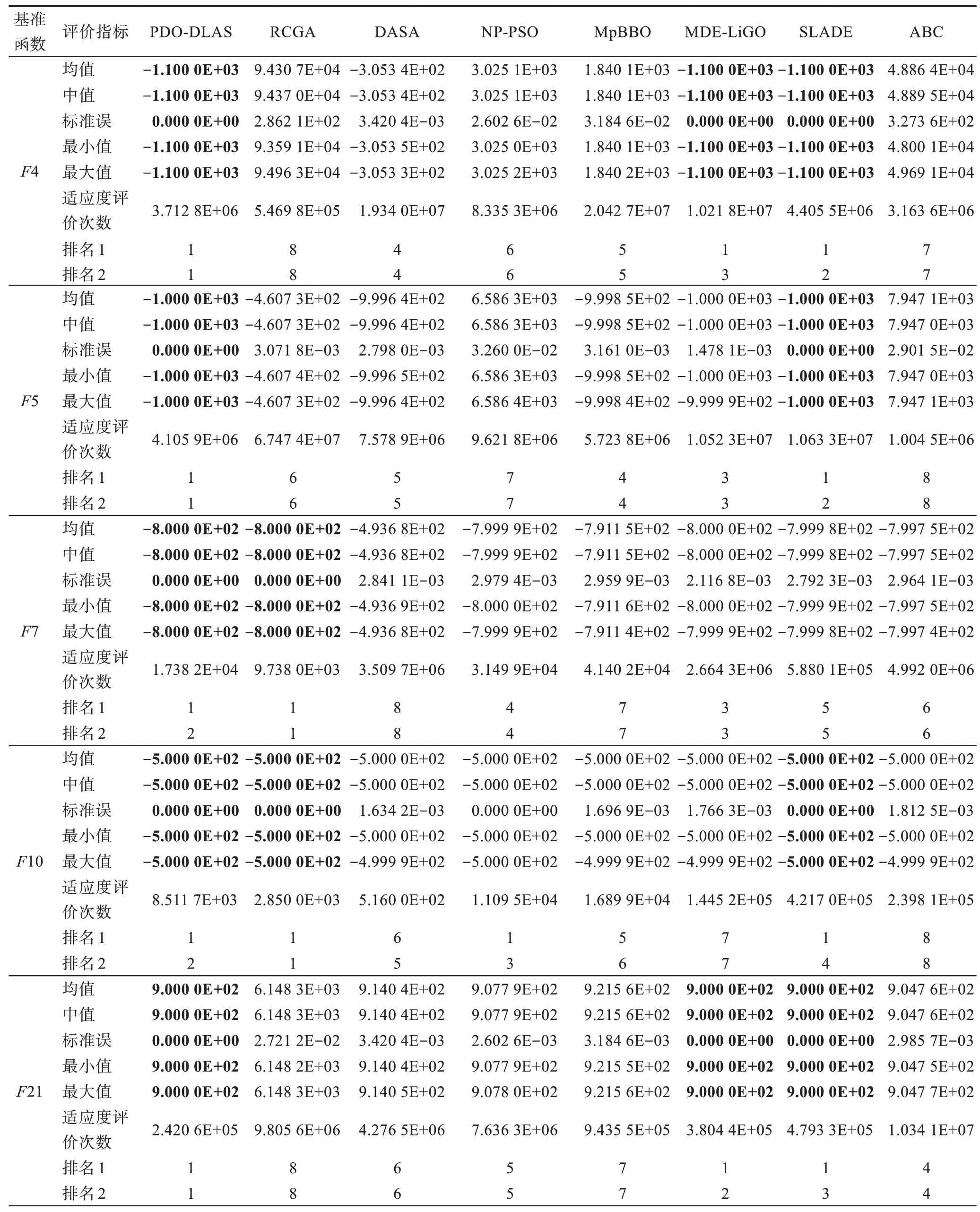
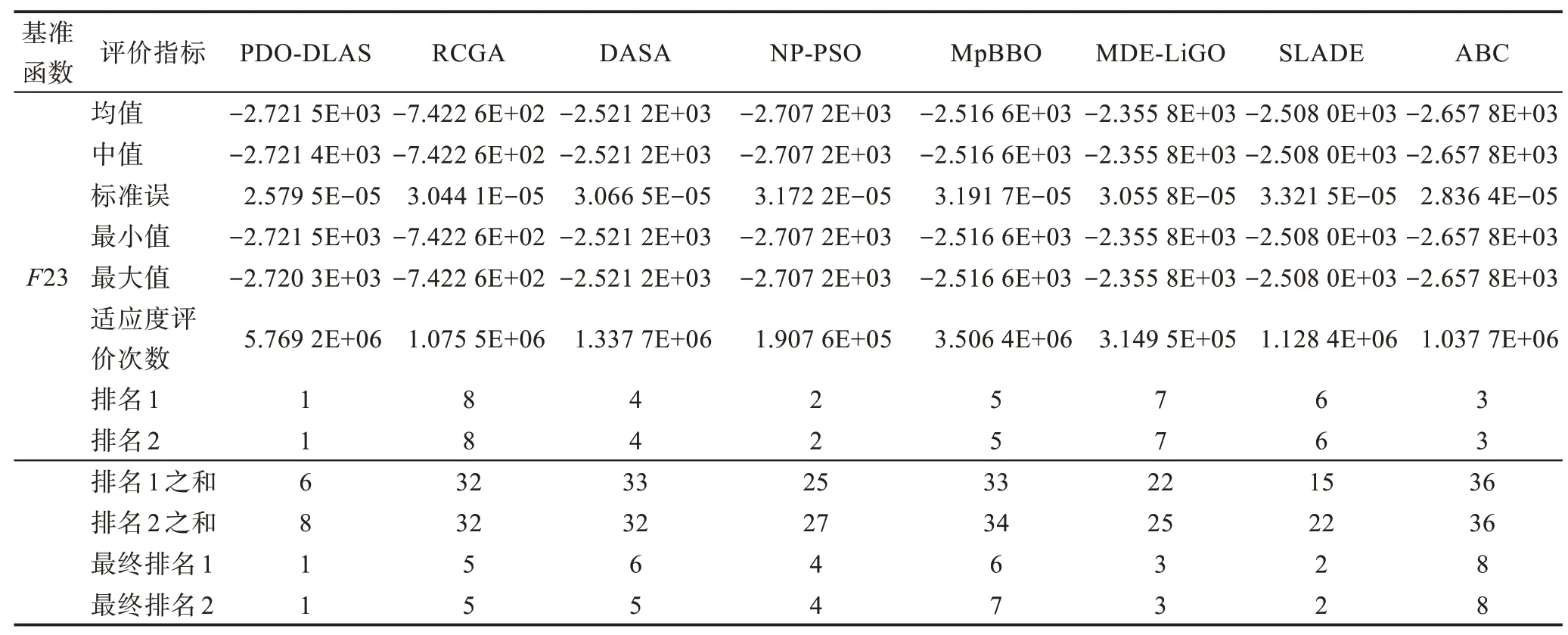
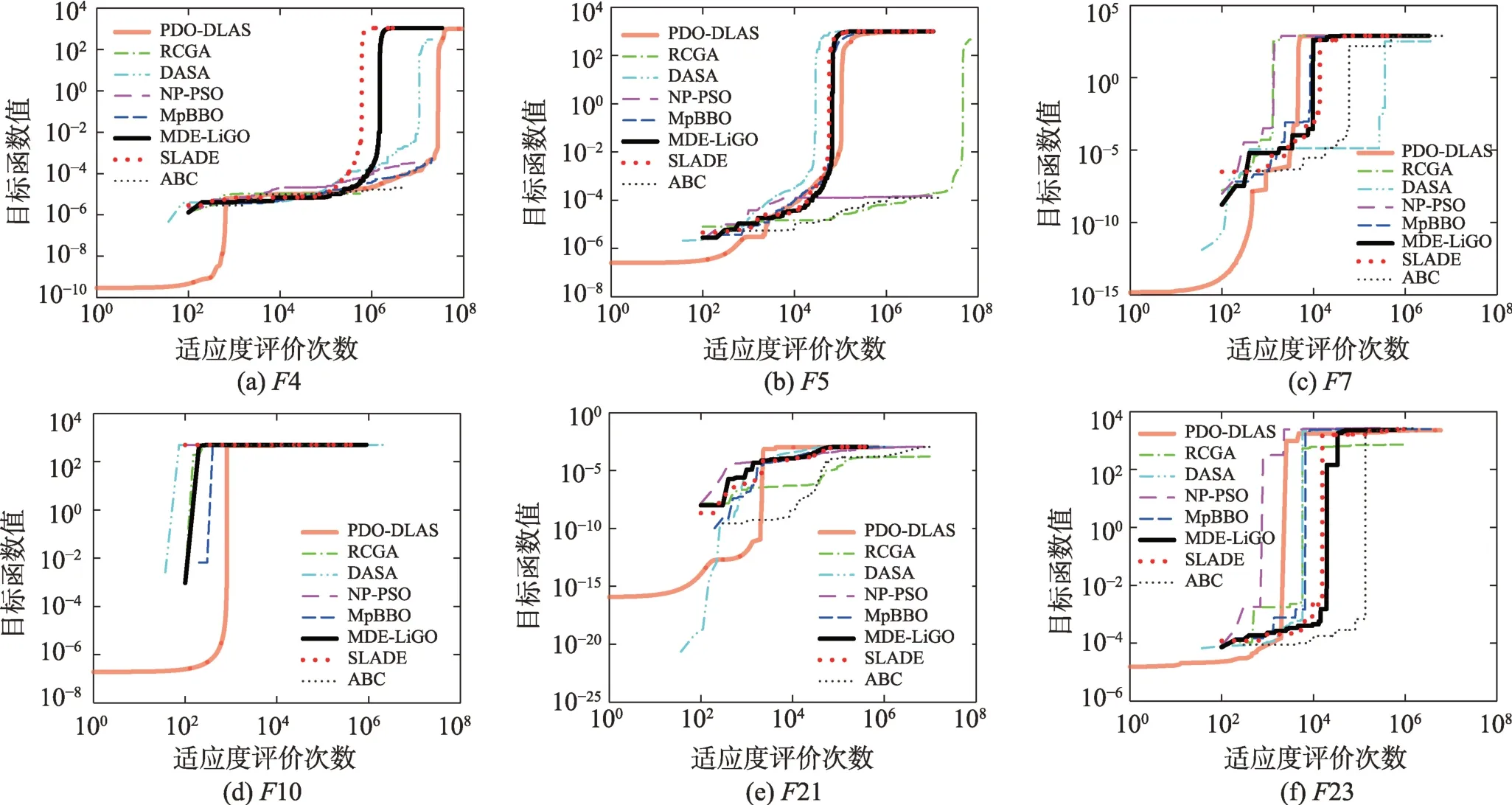
假設(shè)某種群在一個(gè)生態(tài)系統(tǒng)E中生長(zhǎng),該種群由具有不同年齡的生物個(gè)體組成,為簡(jiǎn)單起見,下面將生物個(gè)體簡(jiǎn)稱為個(gè)體。個(gè)體分為雌性(用性別變量u=1 表示)和雄性(用性別變量u=2 表示)兩種類型;種群自然地分成A個(gè)年齡組,A為該種群的最高年齡,0 在時(shí)期t,該種群中的性別為u的個(gè)體總數(shù)為Pu(t),u∈{1,2},即: 每個(gè)個(gè)體都用唯一編號(hào)表示,即性別為u、年齡組為a的個(gè)體編號(hào)集合為{1,2},a=1~A。種群中的每個(gè)個(gè)體都具有n個(gè)特征,且特征數(shù)n不隨時(shí)間變化而改變。時(shí)期t,對(duì)于性別為u、年齡組為a的個(gè)體i來說,用其特征表示就是其中就是性別為u、年齡組為a的個(gè)體i的第j個(gè)特征, 優(yōu)化問題式(1)中的決策變量與個(gè)體的對(duì)應(yīng)關(guān)系如下所述。 時(shí)期t,在式(1)的搜索空間H中隨機(jī)生成的Pu(t)個(gè)試探解是令搜索空間H與生態(tài)系統(tǒng)E相對(duì)應(yīng),則時(shí)期t該生態(tài)系統(tǒng)中Pu(t)個(gè)個(gè)體就與搜索空間H中式(1)的Pu(t)個(gè)試探解一一對(duì)應(yīng),即時(shí)期t性別為u、年齡組為a的個(gè)體i與試探解一一對(duì)應(yīng);更進(jìn)一步,即時(shí)期t性別為u、年齡組為a的個(gè)體i的特征與試探解的分量相對(duì)應(yīng),u∈{1,2}。 在該生態(tài)系統(tǒng)中,個(gè)體的演化規(guī)律如下: (1)個(gè)體的新生是由雌性個(gè)體和雄性個(gè)體交配產(chǎn)生的。 (2)個(gè)體的死亡是因?yàn)閭€(gè)體太虛弱所導(dǎo)致的。 (3)在年齡相近的個(gè)體中,普通個(gè)體會(huì)不分性別地向比它優(yōu)秀的個(gè)體學(xué)習(xí)。 (4)年齡較大的個(gè)體能夠不分性別地對(duì)年齡較小的施加影響。 (5)個(gè)體之間的相互作用表現(xiàn)在對(duì)其特征的影響上,且此相互作用及其所導(dǎo)致的影響是隨時(shí)間變化的。 對(duì)任何一個(gè)個(gè)體來說,按優(yōu)化問題式(1)計(jì)算,其所對(duì)應(yīng)的目標(biāo)函數(shù)值越小,則其適應(yīng)度越高,反之亦然。個(gè)體的適應(yīng)度越高,其生存的概率也越高;而適應(yīng)度越低的個(gè)體,其被淘汰的概率會(huì)越高。也就是說,生態(tài)系統(tǒng)中的個(gè)體的演化規(guī)律符合達(dá)爾文進(jìn)化論規(guī)律。時(shí)期t性別為u、年齡組為a的個(gè)體i的適應(yīng)度用FEI(fitness evaluation index)指數(shù)來表示,其計(jì)算方法為: 假設(shè)表明第a年齡組每一個(gè)個(gè)體在一個(gè)時(shí)段內(nèi)出生的后代(或新生的雌性或雄性)的平均數(shù)為出生率函數(shù),特別地設(shè)它是一個(gè)常數(shù),即: 由所有年齡組的后代相加而得到初始年齡組為: 假設(shè)描述由第a年齡組存活到第a+1 年齡組的比率為存活率函數(shù)它只是第a年齡組個(gè)體數(shù)的線性函數(shù)。 假設(shè)式(4)和式(6)表明不考慮參數(shù)依賴于環(huán)境條件的變化,并且忽略種群大小對(duì)出生率和死亡率的影響。 令Yu(t)=,則由式(5)、式(7)可得到方程: 這里,A×A方陣Lu形如: Lu稱為L(zhǎng)eslie 矩陣,其元素稱為活率或種群統(tǒng)計(jì)參數(shù)。稱式(8)、式(9)為L(zhǎng)eslie模型。 向量Yu(t)以絕對(duì)值而非相對(duì)值顯示了種群大小在各年齡組中的一個(gè)分布,相對(duì)年齡分布稱為年齡普。矩陣Lu確定了A維歐氏空間的一個(gè)線性算子,把這種算子稱為L(zhǎng)eslie算子。因?yàn)樽兞看淼赼年齡組的個(gè)體數(shù),它們是非負(fù)的。矩陣Lu的特征方程為: 如果矩陣Lu有模等于r的h個(gè)特征值,即λ1=r,λ2,…,λh,則所有這些特征值彼此不同,但都是λhrh=0 的根,h稱為矩陣Lu的非本原性指數(shù),它等于那些出生率不為0 的年齡組的編號(hào)的最大公約數(shù)。若h=1,則矩陣Lu稱為素矩陣。 矩陣Lu可表示為: 式中,m為矩陣Lu的不同特征值的個(gè)數(shù);Jj為kj×kj(kj為特征值λj的重?cái)?shù),k1+k2+…+km=A)Jordan塊,其形狀為: Cu(λ)和Ru(λ)的內(nèi)積滿足: (Cu(λa),Ru(λa))=1,(Cu(λa),Ru(λb))=0,a≠b,a,b=1~A 引入極限向量函數(shù): 式(10)、式(11)可以對(duì)Leslie 模型的軌線的漸近性質(zhì)建立一些推斷。 若Lu是素矩陣,則極限向量函數(shù)與t無關(guān),即: 定理1(關(guān)于循環(huán)的平均)[12]設(shè)h為矩陣Lu的非本原性指數(shù),則: 定理2(關(guān)于周期性)[12]設(shè)h為矩陣L的非本原性指數(shù),則極限向量函數(shù)L(Yu,t)關(guān)于t是周期的,周期為: 式中,lcm 表示最小公倍數(shù);l取遍值1,2,…,h;ul/vl為不可約分?jǐn)?shù)(當(dāng)l=1 時(shí),設(shè)ul=0,vl=1)。 這樣,T是非本原性指數(shù)h的因子,并依賴于向量Yu的初始分布。任何情況下,極限分布的總體大小W(Yu,t)的真正周期必須是T的因子,其中W(Yu,t)=真正周期等于T的條件,由下面的定理給出。 定理3(關(guān)于種群總大小的周期)[12]W(Yu,t)的周期一致的充要條件是: 當(dāng)R的值不作為穩(wěn)定性的某種度量時(shí),是所有生物種群再生速率的廣義參數(shù);而作為一種穩(wěn)定性度量時(shí),如果R=1,那么r=1,種群大小不會(huì)作指數(shù)性的減少和增長(zhǎng),而趨于極限分布狀態(tài)。R<1 和R>1 分別表明r<1 和r>1,根據(jù)式(10)和式(12),種群或滅亡或者無限制地增長(zhǎng)。 由式(14)知,成長(zhǎng)系數(shù)R由存活率、出生率函數(shù)和年齡組數(shù)A決定。當(dāng)確定后,可確定能夠確保R=1 的A。 定理4(循環(huán)周期)[12]設(shè)Lu是一具有單位主特征值和非本原性指數(shù)h的Leslie 矩陣,則在模型式(8)的軌線之間存在循環(huán),如果循環(huán)有周期k,則k是h的因子。 時(shí)期t,對(duì)當(dāng)前性別為u、年齡組為a的個(gè)體i來說,其特征個(gè)體集合的生成策略如下: (1)優(yōu)勢(shì)個(gè)體集合SIu,a(t)。從個(gè)個(gè)體中隨機(jī)選出M個(gè)個(gè)體,這些個(gè)體的FEI 指數(shù)要比當(dāng)前個(gè)體要高,形成優(yōu)勢(shì)個(gè)體集合SIu,a(t),M稱為特征個(gè)體數(shù)。 (2)普通個(gè)體集合GIu,a(t)。從個(gè)個(gè)體中隨機(jī)選出M個(gè)個(gè)體,形成普通個(gè)體集合GIu,a(t)。 演化算子設(shè)計(jì)方法如下: (1)新生算子。該算子描述種群內(nèi)個(gè)體的新生。從雌性和雄性優(yōu)勢(shì)個(gè)體集合SIu,a(t)中各隨機(jī)選擇一個(gè)個(gè)體進(jìn)行交配,產(chǎn)生新個(gè)體i,其性別隨機(jī)確定,所處年齡組為第1 組。 式中,w在{1,2}隨機(jī)選擇;α=Rnd(0,1),Rnd(a,b)為在區(qū)間[a,b]內(nèi)產(chǎn)生滿足均勻分布的隨機(jī)數(shù);a=A0~A,A0為雌性個(gè)體生育的起始年齡;iu在中隨機(jī)選擇,u∈{1,2};J0為在1~n中隨機(jī)選擇M個(gè)特征所形成的集合。由式(15)形成的新個(gè)體為 (2)死亡算子。該算子描述種群內(nèi)個(gè)體的死亡。時(shí)期t,從性別為u、年齡組為a的個(gè)體集合中,選出FEI指數(shù)最低的個(gè)體,將其刪除。 (3)學(xué)習(xí)算子。該算子描述的是處于相近年齡的普通個(gè)體會(huì)向其優(yōu)勢(shì)個(gè)體學(xué)習(xí),從而使得優(yōu)勢(shì)個(gè)體的一些特征傳遞給普通個(gè)體。與年齡組a相近的年齡組取為U={a-M,a-M+1,…,a,a+1,…,a+M},對(duì)于每個(gè)年齡組b∈U,任意選擇被學(xué)習(xí)的個(gè)體性別w,令Q(b)=w,w∈{1,2};進(jìn)一步令則對(duì)于性別為u、年齡組為a的當(dāng)前個(gè)體i來說,有: (4)影響算子。該算子描述的是年齡較大的個(gè)體的一些行為會(huì)對(duì)年齡小的個(gè)體造成影響。比年齡組a大的年齡組取為V={a+1,a+2,…,a+M},對(duì)于每個(gè)年齡組b∈V,任意選擇施加影響的個(gè)體性別w,令Z(b)=w,w∈{1,2};進(jìn)一步令則對(duì)于性別為u、年齡組為a的當(dāng)前個(gè)體i來說,有: 式中,YP=GP1?GP2。 (5)進(jìn)化算子。個(gè)體的進(jìn)化須滿足達(dá)爾文進(jìn)化論規(guī)律。對(duì)于性別為u、年齡組為a的當(dāng)前個(gè)體i,其進(jìn)化算子的定義如下: 假設(shè)優(yōu)化問題搜索空間的維數(shù)為n,每個(gè)變量的搜索區(qū)間為[li,ui],i=1~n,利用正交拉丁方生成方法產(chǎn)生W個(gè)初始解的正交表LM(Wn)的構(gòu)造算法如算法INIT 所述。 算法1INIT(W)//產(chǎn)生W個(gè)初始解的正交表LM(Wn)的構(gòu)造算法 步驟1計(jì)算每個(gè)變量的離散點(diǎn)yij: yij=li+(j-1)(ui-li)/(W-1),i=1~n;j=1~W 步驟2根據(jù)正交拉丁方的生成方法計(jì)算初始解xij: xij=yjk,i=1~W,j=1~n 式中,k=(i+j-1)modW;若k=0,則k=W。 算法INIT(W)所確定的W個(gè)初始解Xi=(xi1,xi2,…,xin),i=1~W,具有很好的均衡分散性和整齊可比性。 算法2PDO-DLAS 步驟1初始化 步驟2執(zhí)行下列操作 1.6.1 時(shí)間復(fù)雜度 PDO-DLAS 算法的時(shí)間復(fù)雜度計(jì)算如表1 所示,其中 1.6.2 PDO-DLAS 算法的全局收斂性證明 定理5PDO-DLAS 算法具有全局收斂性。 證明(1)從新生算子、學(xué)習(xí)算子、影響算子、生長(zhǎng)算子的定義式(15)~式(18)可知,滿足關(guān)系表明PDO-DLAS 算法的演變過程具有Markov 特性;(2)從生長(zhǎng)算子的定義式(18)知,任一個(gè)體的FEI 指數(shù)總是保持遞增態(tài)勢(shì)。依據(jù)文獻(xiàn)[23]可知,滿足上述兩個(gè)特性的PDO-DLAS算法具有全局收斂性,其相關(guān)證明可參見文獻(xiàn)[23],本文不再贅述。 Table 1 Time complexity表1 時(shí)間復(fù)雜度 PDO-DLAS 算法的參數(shù)由Leslie 模型參數(shù)和運(yùn)行控制參數(shù)兩部分組成,前者是算法的內(nèi)置參數(shù),一旦設(shè)定,無需修改;后者需要根據(jù)所求優(yōu)化問題的實(shí)際特征進(jìn)行人工設(shè)置。 依據(jù)1.2 節(jié)的結(jié)論,Leslie 模型參數(shù)設(shè)置應(yīng)滿足如下要求: (2)從定理2 和定理3 知,軌線的性質(zhì)依賴于時(shí)間尺度的選擇,故應(yīng)避免模型軌線的周期性。例如,可合并時(shí)間間隔或延長(zhǎng)時(shí)段,使得有非零出生率的年齡組成為相鄰的。 (3)從定理4 知,應(yīng)盡量使得Lu的主特征值不等于1,從而確保模型式(8)的軌線之間存在循環(huán)。 依據(jù)上述要求,Leslie 模型式(4)、式(6)和式(9)中的參數(shù)可按下列方式設(shè)置:A=20,A0=A/2,h=A0+1=11,n0=30,n1=50;b0=3,b1=5;s0=0.65,s1=0.846。此時(shí),個(gè)體總數(shù)隨演化周期的變化如圖1所示。由式(14)計(jì)算得R=1.000 378 ≈1;Lu的主特征值λ=1.000 3 ≈1,式(8)的軌線之間的循環(huán)周期為11 個(gè)演化周期。從圖1 可知,各年齡組個(gè)體數(shù)趨向極限分布,且具有很好的變化特征。 Fig.1 Changing rule of total number of individuals with time圖1 個(gè)體總數(shù)隨時(shí)間的變化規(guī)律 含有n個(gè)變量的Michalewicz 函數(shù)優(yōu)化問題具有n!個(gè)局部極小點(diǎn)。例如,對(duì)于50 維優(yōu)化問題,Michalewicz 函數(shù)有高達(dá)50!=3.041 41×1064個(gè)局部極小點(diǎn)。因此,搜索過程極易陷入局部最優(yōu)解陷阱。目前,該函數(shù)的理論全局最優(yōu)解還未可知,尋找該函數(shù)的全局最優(yōu)解具有很大的挑戰(zhàn)性。Michalewicz 函數(shù)優(yōu)化問題如下: 本文以求解Michalewicz 函數(shù)優(yōu)化問題為例來確定PDO-DLAS 算法中的運(yùn)行控制參數(shù)的適當(dāng)設(shè)置,這些參數(shù)包括如下幾類: (1)G和ε。這兩個(gè)參數(shù)是互補(bǔ)參數(shù),只要滿足其中一個(gè)即可。通常取G=106~1010,ε=10-10~10-5。 (2)E0和M。這兩個(gè)參數(shù)對(duì)PDO-DLAS 算法的性能影響較大,下面重點(diǎn)討論這兩個(gè)關(guān)鍵參數(shù)的取值規(guī)律。 令n=50,E0=0.01,G=108,PDO-DLAS 算法運(yùn)行100 次,表2 描述了M與最優(yōu)目標(biāo)函數(shù)值的平均值(AvgOFV)和計(jì)算時(shí)間的平均值(AvgCT)之間的關(guān)系。表2 表明,當(dāng)M=3~6 時(shí),AvgOFV的精度達(dá)到最佳,而AvgCT遞增不大。因此,建議M=3~6。 Table 2 Relationship of M with AvgOFV and AvgCT表2 M 與AvgOFV 和AvgCT 之間的關(guān)系 令n=50,M=3,G=108,PDO-DLAS 算法運(yùn)行100 次,表3 描述了E0、AvgOFV和AvgCT之間的關(guān)系。結(jié)果表明,當(dāng)E0=0.004~0.100 時(shí),AvgOFV精度較高,但AvgCT增加不大;當(dāng)E0>0.100 時(shí),AvgCT增加很大,但AvgOFV精度也大大降低;尤其當(dāng)E0=1.000時(shí),無法得到最優(yōu)解。因此,當(dāng)E0=0.004~0.100 時(shí),PDO-DLAS 算法性能最好。 Table 3 Relationship of E0 with AvgOFV and AvgCT表3 E0 與AvgOFV 和AvgCT 之間的關(guān)系 CEC2013[24]是一個(gè)國(guó)際上專門用來測(cè)試智能優(yōu)化算法的測(cè)試包,該測(cè)試包中包含有28 個(gè)優(yōu)化問題,每個(gè)優(yōu)化問題由一些著名的傳統(tǒng)優(yōu)化問題組合而成。這些優(yōu)化問題不但克服了傳統(tǒng)優(yōu)化問題的一些缺陷(如全局最優(yōu)解關(guān)于原點(diǎn)對(duì)稱、條件數(shù)過低等),而且其求解難度均大幅提高。本文在該測(cè)試包中選擇6 個(gè)難度很大的優(yōu)化問題來對(duì)PDO-DLAS 算法與其他算法進(jìn)行比較,如表4 所示。 Table 4 6 optimization problems表4 6 個(gè)優(yōu)化問題 表4 中,O是隨機(jī)產(chǎn)生的n維向量。求解這些優(yōu)化問題時(shí),PDO-DLAS 算法的參數(shù)設(shè)置是n=50,G=108,ε=10-8,E0=0.01,M=3。與PDO-DLAS 算法進(jìn)行比較的7 種智能優(yōu)化算法為RCGA(real-coded genetic algorithm)[25]、DASA(differential ant-stigmergy algorithm)[26]、NP-PSO(non-parametric particle swarm optimization)[27]、MpBBO(metropolis biogeographybased optimization)[28]、MDE-LiGO(modified differential evolution with locality induced genetic operators)[29]、SLADE(self-adaptive differential evolution)[30]、ABC(artificial bee colony)[31],這些算法各參數(shù)設(shè)置可參見其對(duì)應(yīng)文獻(xiàn)。 求解各個(gè)優(yōu)化問題時(shí),每個(gè)算法均獨(dú)立求解51次。表5 給出了各算法的求解結(jié)果。其中,表5 的列是所有參與比較的優(yōu)化算法,表5 的行是求解每個(gè)優(yōu)化問題時(shí)所獲得的關(guān)鍵對(duì)比參數(shù),即各算法所獲得的最優(yōu)解的均值、中值、標(biāo)準(zhǔn)誤、最小值、最大值、適應(yīng)度評(píng)價(jià)次數(shù)。 從表5 可以看出,這8 個(gè)算法按最終排名1 進(jìn)行排序所得的結(jié)果均如下: PDO-DLAS>MDE-LiGO>SLADE>NP-PSO>RCGA>DASA=MpBBO>ABC 按最終排名2 進(jìn)行排序所得的結(jié)果均如下: PDO-DLAS>MDE-LiGO>SLADE>NP-PSO>RCGA=DASA>MpBBO>ABC 圖2(a)~(f)給出了各算法求解6 個(gè)優(yōu)化問題時(shí)的樣本收斂曲線。各圖樣本曲線之間的差異可以用PDO-DLAS 算法的探索和求解過程來說明。 Table 5 Solution results of each algorithm表5 各算法的求解結(jié)果 表5(續(xù)) (1)對(duì)于圖2(a),PDO-DLAS 算法在區(qū)間[0,102]、[102,103]、[103,107]、[107,108]搜索期間,搜索分別處于求精狀態(tài)、探索狀態(tài)、再求精狀態(tài)、快速探索狀態(tài)轉(zhuǎn)求精狀態(tài),而進(jìn)行“求精→探索→再求精→快速探索”的狀態(tài)轉(zhuǎn)換等價(jià)于不斷從局部最優(yōu)解陷阱跳出的行為;其他算法在區(qū)間[0,102]、[102,106]、[106,108]處于初始化狀態(tài)、求精狀態(tài)、探索狀態(tài)轉(zhuǎn)再求精狀態(tài)。PDO-DLAS、MDE-LiGO、SLADE 具有最終的相同求解精度,其他算法最終的求解精度均很低。 Fig.2 Sample convergence curves圖2 樣本收斂曲線 (2)對(duì)于圖2(b),PDO-DLAS算法在區(qū)間[0,102]、[102,5×105]、[5×105,9×105]、[9×105,108]搜索期間,搜索分別處于求精狀態(tài)、緩慢探索狀態(tài)、快速探索狀態(tài)、再求精狀態(tài),即進(jìn)行“求精→緩慢探索→快速探索→再求精”的狀態(tài)轉(zhuǎn)換,實(shí)施相應(yīng)的局部最優(yōu)解陷阱逃逸操作;DASA、MpBBO、MDE-LiGO、SLADE 算法在區(qū)間[0,102]、[102,5×105]、[5×105,9×105]、[9×105,108]搜索期間,處于初始化狀態(tài)、緩慢探索狀態(tài)、快速探索狀態(tài)、求精狀態(tài);RCGA、NP-PSO、ABC 算法在區(qū)間[0,102]、[102,9×107]搜索期間,搜索分別處于初始化狀態(tài)、緩慢求精或緩慢探索狀態(tài),RCGA 在[9×107,108]期間進(jìn)入快速探索狀態(tài)。PDO-DLAS、MDELiGO、SLADE 具有最終的相同求解精度,其他算法最終的求解精度均很低。 采用上述類似的分析方法,可以分析圖2(c)~圖2(f),本文不再重復(fù)。 本文基于種群具有離散Leslie 年齡結(jié)構(gòu)的動(dòng)力學(xué)模型提出了一種具有全局收斂性的新型優(yōu)化算法,與其他典型群智能算法相比,PDO-DLAS 算法具有如下特點(diǎn): (1)個(gè)體依據(jù)其年齡組和性別被自動(dòng)劃分成2A類,每類個(gè)體數(shù)依據(jù)Leslie 模型自動(dòng)進(jìn)行動(dòng)態(tài)計(jì)算,這樣既大幅增加了個(gè)體的多樣性,又避免了人工確定個(gè)體數(shù)的困難。 (2)所有算子是通過利用Leslie 模型以及同齡組和不同齡組個(gè)體間的相互作用關(guān)系進(jìn)行構(gòu)造的,PDO-DLAS 算法與所求解的實(shí)際優(yōu)化問題無關(guān),故具有很好的普適性。 (3)PDO-DLAS 算法中的每個(gè)算子具有明確功能,其中學(xué)習(xí)算子可實(shí)現(xiàn)年齡組相近個(gè)體之間的信息交換;影響算子可實(shí)現(xiàn)不同齡組個(gè)體之間的信息交換;新生算子可增加強(qiáng)壯個(gè)體數(shù);死亡算子可以減少虛弱個(gè)體數(shù);進(jìn)化算子可確保算法具有全局收斂性。 (4)采用正交拉丁方方法生成初始試探解可確保其具有均衡分散性和整齊可比性。 (5)采用Leslie 模型的機(jī)理確定PDO-DLAS 算法中的相關(guān)參數(shù),大幅減少了PDO-DLAS 算法參數(shù)的人工確定個(gè)數(shù)。實(shí)際上,PDO-DLAS 算法需要人工確定的參數(shù)只有2 個(gè)。 (6)在進(jìn)行迭代計(jì)算時(shí),PDO-DLAS 算法每次只處理個(gè)體特征數(shù)的1/250~1/10,從而使時(shí)間復(fù)雜度大幅降低。因此,PDO-DLAS算法適于求解高維優(yōu)化問題。 PDO-DLAS 算法的下一步改進(jìn)方向如下: (1)深入研究學(xué)習(xí)算子、影響算子、新生算子和死亡算子的動(dòng)態(tài)特征。 (2)深入研究個(gè)體的動(dòng)態(tài)特征。
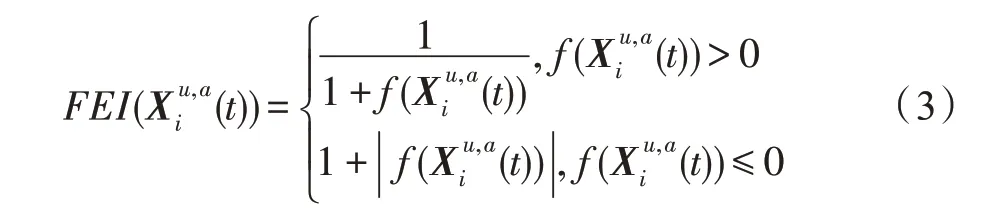
1.2 Leslie種群離散模型
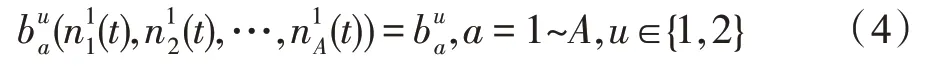
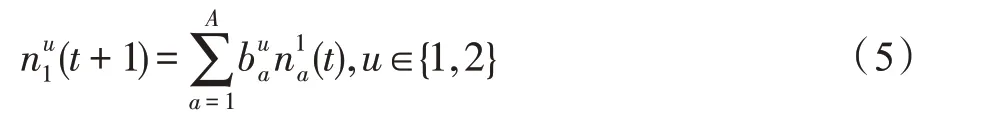
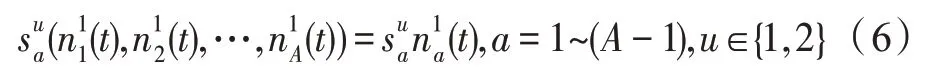
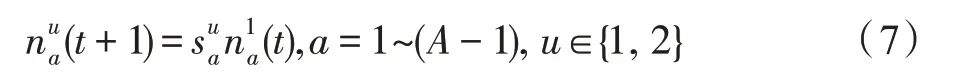
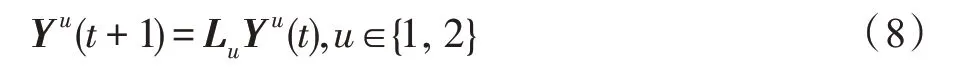
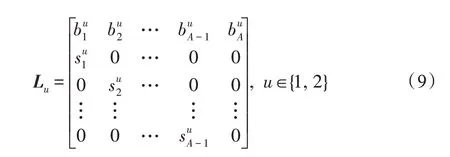
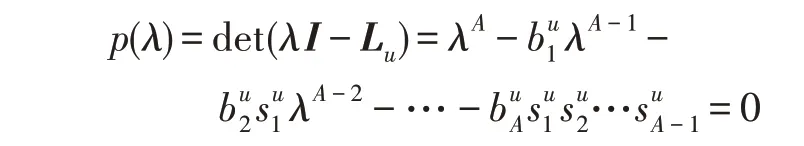
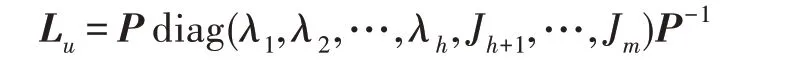


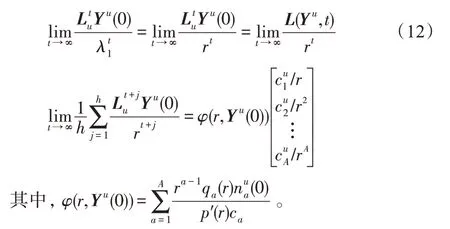
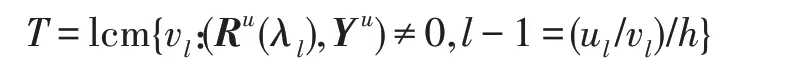

1.3 演化算子設(shè)計(jì)
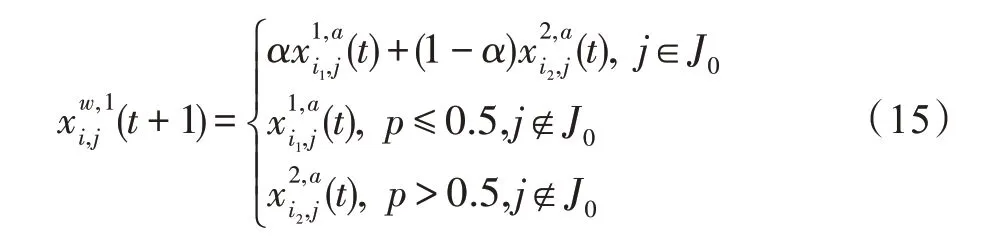
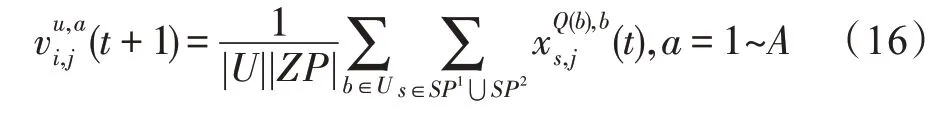
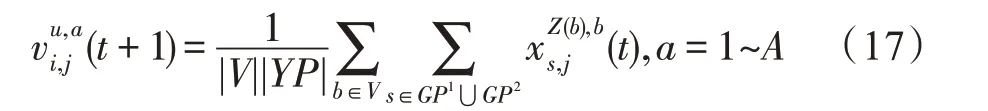
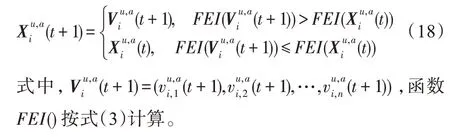
1.4 個(gè)體初始化
1.5 PDO-DLAS 算法構(gòu)造



1.6 算法特點(diǎn)分析
2 參數(shù)確定
2.1 Leslie模型參數(shù)設(shè)置方法
2.2 運(yùn)行控制參數(shù)設(shè)置方法
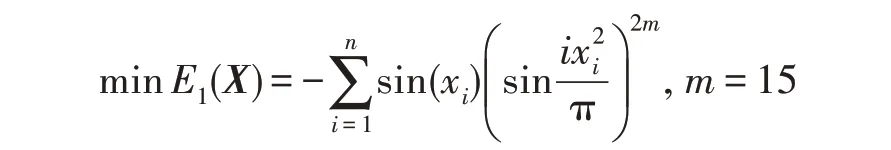
3 PDO-DLAS 算法與其他算法的比較
4 結(jié)束語

