基于預處理的快速冪算法及其實現*
段學松,曲中水,江緒楨,呂昌昊
(哈爾濱理工大學 計算機科學與技術學院,黑龍江 哈爾濱 150080)
1 概述
快速冪算法,即快速計算一個數或者矩陣的冪次的算法,一直是加密算法中的重要算法,并且在數論中有著相當廣泛的應用,更是算法競賽中最常遇到的問題,尤其在線性齊次遞推數列[1]的求解上。例如常見的斐波那契數列[1]第n 項的計算,通過構造轉移矩陣[1]和快速計算矩陣冪次[1]的方式能夠大大降低計算線性齊次遞推數列的時間復雜度。但是隨著矩陣的行數和列數不斷增加,每一次矩陣乘法會變得相當耗時,對于稀疏矩陣,雖然存在優化算法[2],甚至存在優化算法的硬件實現[3],但是如何減少矩陣乘法計算的次數變得極其重要。目前計算快速冪,最常用的算法是二進制拆分法[4],但是對于一個固定的數或者是固定矩陣的冪次來說,二進制拆分法并沒有保留每次拆分的過程,導致拆分的過程會做大量的重復計算。因此對于固定的數或者固定矩陣的冪次,可以預處理部分數據,達到減少重復運算,降低算法時間復雜度的目的。
2 傳統的二進制拆分快速冪算法概述
2.1 二進制拆分法的原理
計算an,傳統的快速冪算法的核心思想是二進制拆分。令m 為n 在二進制下最高位1 的位置,我們對n 進行二進制拆分,則有:

通過乘法原理,可以得到:

綜上,可以得到:

其中,ei是n 在二進制下第i 位的值,例如當n=13的時候,n 的二進制形式為:(1101)2,最高位 1 的位置 m=4,對n 進行二進制拆分得到的結果為:
2.2 二進制拆分快速冪算法的時間復雜度與空間復雜度分析
T(n)=O(log2n)
由于二進制拆分快速冪算法用迭代實現,在計算的過程中用于存儲計算用到的空間是常數級別的,因此二進制拆分快速冪算法的空間復雜度為:
S(n)=O(1)
如果計算k 次,總時間復雜度為:
T(n)=O(klog2n)
金壇區于2016年啟動長蕩湖清淤工程,在外源污染有效治理和控制的前提下,通過對長蕩湖湖區污染底泥實施生態清淤,有效削減底泥內源污染,促進湖泊水體水質改善,為長蕩湖水生態修復奠定基礎。
總空間復雜度為:
S(n)=O(1)
2.3 二進制拆分快速冪算法的C++實現

圖1 二進制拆分法的C++實現
2.4 多次計算時二進制拆分法的重復運算
當利用二進制拆分快速冪算法多次計算相同底數的冪次時,存在大量的冗余計算。例如:

3 基于預處理的快速冪算法
3.1 基于預處理的快速冪算法原理
首先我們用a mod b 表示a 對b 取余數。

證明 由取余運算的性質[5]可得,定理1 成例。

證畢。
根據定理2 以及乘法原理可得:

由于 u∈[0,P],v∈(0,P),因此可以在計算快速冪前預處理出 a0,a1,a2…aP-1,aP以及(aP)0,(aP)1,(aP)2…(aP)P-1,(aP)P并存儲起來,每次計算an時,首先計算出以及v=n mod P,之后從提前預處理的數據中選擇(aP)u和av進行一次乘法運算即可得到an的結果。
3.2 基于預處理的快速冪乘算法的時間復雜度與空間復雜度分析
3.2.1 預處理過程時間與空間復雜度分析
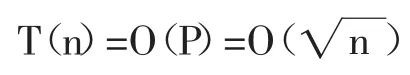
因為通過預處理能夠得到aP,因此,預處理(aP)0,(aP)1,(aP)2…(aP)P-1,(aP)P的時間復雜度:

所以,預處理的總時間復雜度:


3.2.2 計算快速冪的時間與空間復雜度分析
在計算快速冪的過程中,由于P,u,v 的計算消耗是常數級別的,而計算查表計算一次乘法的時間復雜度也是常數級別的,因此計算快速冪的時間復雜度:
T(n)=O(1)
計算過程中臨時變量的存儲空間都是常數級別的,因此計算快速冪的空間復雜度為:
S(n)=O(1)
3.2.3 計算k 次相同底數的an的總體時間空間復雜度分析
預處理的目的是去除重復運算,對于相同的底數,多次計算快速冪只用進行一次預處理操作,k 次計算快速冪的總體時間復雜度是:

總體空間復雜度為:

3.3 基于預處理的快速冪乘算法的C++實現

圖2 基于預處理的快速冪算法的C++實現
4 結束語
本文分析了二進制拆分快速冪算法的缺點,并針對相同底數的多次快速冪運算,提出了一種基于預處理的快速冪算法,通過預處理少量的數據,將時間復雜度為O(klog2n)求冪的算法優化至并給出了該算法的時間復雜度與空間復雜度的分析以及C++編程實現,為求解快速冪提供了新的思路。今后,隨著程序設計應用的不斷深入以及人們對算法的研究,更多更復雜的數學問題必定會迎刃而解。

