陣列旋轉對功率倒置算法性能的影響分析

戴鑫志，李瑞丹，陳飛強，賈 珣

(1.北京衛星導航中心，北京 100081； 2.32022部隊，武漢 430000； 3.國防科技大學，長沙 410005)

0 引言

面對日益擁擠的電磁頻譜和復雜的電磁環境，衛星導航信號由于到達地面時功率非常微弱而極其容易受到各種有意或者無意的干擾，因此現代衛星導航接收機一般都會采取一定的抗干擾措施，以確保接收機在干擾環境下的生存能力。

陣列天線抗干擾由于對干擾類型不敏感、抗干擾能力強等優點，是目前導航接收機最有效的抗干擾措施之一[1]。決定陣列天線接收機抗干擾能力的關鍵之一是抗干擾算法，根據能否在期望信號方向形成增益，抗干擾算法可分為波束形成類和零陷類算法。波束形成類算法的代表是最小方差無失真響應(Minimum Variance Distortionless Respo-nse, MVDR)算法[2-3]和最小均方誤差(Minimum Mean Square Error, MMSE)算法[4]等，能夠在零陷干擾的同時在期望信號方向形成增益，但是算法實現時需要先驗信息作為輸入條件。零陷類算法的代表是功率倒置(Power Inversion, PI)算法[5-6]，PI算法能夠在干擾方向上形成零陷，但不能對期望信號形成增益。不過由于PI算法不需要先驗信息輔助、計算復雜度相對較小、易于工程實現等優點，在實際的陣列天線接收機中得到了大量的應用[7-8]，因此本文主要結合PI算法展開研究。

事實上除了抗干擾算法，陣列天線接收機的抗干擾能力還與陣列構型有關[9-10]，其內在機理是：陣列構型能夠影響干擾信號與導航信號的空間相關系數，進而影響天線陣的抗干擾能力。其實，除了陣列構型，從空間相關系數的定義[11]可以看出，信號的來波方向也是影響空間相關系數的重要因素。文獻[12]和文獻[13]中已經發現，通過控制陣列旋轉，可以降低干擾信號和導航信號的空間相關系數，提升抗干擾后輸出信干噪比，但是沒有進一步分析其內在機理并發現一般性的規律。總之，目前鮮有文章專門研究陣列旋轉對PI算法抗干擾能力的影響，本文通過理論推導的方法建立了信號來波方向與PI算法抗干擾處理后陣列增益的關系，在此基礎上，通過數值計算的方法分析了陣列增益隨陣列旋轉的變化規律，分析結果表明，通過陣列旋轉能夠改善PI算法的抗干擾性能。

1 陣列信號模型

不失一般性，假設天線陣陣元個數為N且第1個陣元作為參考陣元位于空間坐標系原點處。為便于理論分析，假設遠場處有1個期望信號s(t)和1個干擾信號J(t)入射到天線陣,則天線陣的接收信號x(t)可表示為

x(t)=ass(t)+aJJ(t)+n

(1)

式中，as表示期望信號導向矢量;aJ表示干擾導向矢量;n表示方差為σ2的陣列通道噪聲。信號導向矢量的定義[14]如下

(2)

其中，λ表示信號載波波長；zn,n=1,2,…,N表示一個3×1的指向陣元位置的矢量；d表示一個3×1的指向信號源位置的矢量。

假設干擾信號與期望信號不相關，因此接收信號的自相關矩陣Rxx為

Rxx=Rss+Rjj+σ2I

(3)

式中,Rss表示期望信號的自相關矩陣；Rjj表示干擾的相關矩陣；σ2I表示噪聲的自相關矩陣，I表示一個單位矩陣。

天線陣抗干擾后，輸出信號y(t)可表示為

y(t)=wHx(t)

(4)

式中，w表示陣列權矢量；[·]H表示共軛轉置。

PI算法下，陣列權矢量由式(5)計算

(5)

(6)

式中，PJ表示干擾信號的功率。

將式(6)代入式(5)式,有

(7)

經過抗干擾處理后，期望信號輸出為

ys=wHass(t)

(8)

其中，ρ表示干擾信號與期望信號的空間相關系數，其定義由式(9)給出

(9)

為便于比較陣列輸出信號與單天線輸出信號的差異，將式(5)中的權矢量w歸一化,有

(10)

經陣列處理后，輸出期望信號可表示為

(11)

則輸出信噪比為

(12)

式中，ps表示單天線接收信號時的信號功率;pn表示噪聲功率;|?|表示取模運算。而單天線接收信號時，輸出信噪比為

(13)

利用式(12)和式(13)可得出陣列相較于單天線對期望信號的增益，即陣列增益為

(14)

經過理論推導，有如下結果

(15)

(16)

因此有

(17)

式(17)即為PI算法下，天線陣對期望信號增益的具體表達式，它與抗干擾后輸出載噪比的關系為

(18)

(19)

式(19)中雖然已經體現了PI算法抗干擾處理后陣列增益與空間相關系數的關系，但還沒有建立陣列增益與信號來波方向的聯系，因此還需要進一步分析。

2 陣列旋轉對陣列增益影響分析

對常見的四陣元Y型陣列進行分析，其陣列構型如圖1所示。

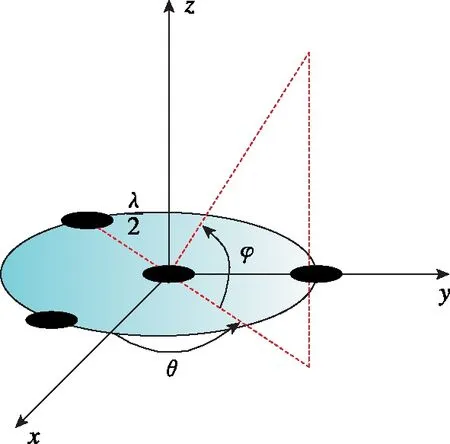
圖1 四陣元Y型陣列模型Fig.1 Four-element Y-array pattern

假設導航信號和干擾信號的方位角和俯仰角信息分別為：(θs,φs)，(θJ,φJ)。由式(2)可得期望信號和干擾信號的導向矢量分別為

(20)

(21)

令導航信號與干擾信號在方位角上的間隔為Δ，即θJ=θs+Δ。由式(9)可得導航信號與干擾信號的空間相關系數為

(22)

假設天線陣在水平面內旋轉，這意味著導航信號俯仰角φs、干擾信號俯仰角φJ以及方位角間隔Δ均不隨陣列旋轉而改變，式(22)中只有方位角θs會隨著陣列旋轉在[0,2π]范圍內連續變化。保留變化量θs，將式(22)經過適當化簡后，有

(23)

其中

(24)

進一步，由式(19)可以得到PI算法抗干擾處理后，陣列對導航信號的增益為

G=

(25)

式(25)形式比較復雜，但可以通過一些方法研究陣列增益G的一些性質。首先，通過式(25)中陣列增益的表達式不難得出：陣列增益G的取值受到方位角θs、導航信號俯仰角φs、干擾信號俯仰角φJ以及方位角間隔Δ這4個因素的影響。并且如果把陣列增益G看作一個函數G(θs)，則G(θs)是一個連續函數。

(26)

由于推導過程并不復雜，這里不給出詳細的推導過程。當然，式(26)僅針對四陣元Y型陣列，不難得出對于其他具有幾何對稱性的天線陣，G(θs)將有其他的周期。

陣列增益G(θs)還有其他的一些性質，可以通過數值計算的方法得到。需要說明的是，G(θs)是一個連續的、周期性的函數，對于任意形狀的天線陣都是成立的，其連續性可以通過復合函數的性質得到，周期性可以通過三角函數的性質得到。此外在理論分析過程中，均假設只存在一個干擾源，主要是考慮到對于多干擾存在時，數學表達式非常復雜，有的甚至難以用數學表達式描述。在后續的仿真實驗中，將研究多個干擾源同時存在的情況。

3 數值分析

數值計算時，考慮到實際條件下干擾信號一般來自低仰角，而接收機進行定位解算時一般不取仰角過低的衛星，因此式(25)中可以取干擾俯仰角φJ∈[1°,15°]，信號俯仰角φs∈[10°,90°]，方位角θs∈[1°,360°]，方位角間隔Δ∈[0°,360°]。

取干擾信號俯仰角為5°，信號俯仰角為40°，天線陣旋轉角度為360°，在方位角間隔分別為90°和150°時，利用式(25)畫出陣列增益變化曲線如圖2所示。

圖2 陣列增益變化曲線Fig.2 Array gain curve

從圖2可以看出，隨著陣列旋轉，不同方位角間隔下的陣列增益均以60°為周期連續變化，并且每個周期內，陣列增益存在一個最大值和一個最小值。通過計算機遍歷所有的數值組合發現，得到的陣列增益隨陣列旋轉的變化曲線都是相似的，只是陣列增益波動的范圍不同而已。由此可以得出G(θs)的另一個重要性質：在每個周期內，G(θs)存在一個最大值Gmax和一個最小值Gmin，最值的大小受到方位角間隔、導航信號俯仰角和干擾信號俯仰角的影響。

陣列增益曲線最大值Gmax與最小值Gmin之差Gmax-Gmin體現了陣列旋轉時抗干擾輸出載噪比的最大改善程度，也即對PI算法抗干擾性能的最佳改善程度。下面重點分析了陣列增益曲線中Gmax-Gmin的變化趨勢。固定干擾信號俯仰角為5°，天線陣旋轉角度為360°，方位角間隔從1°遍歷至360°，導航信號俯仰角從10°遍歷至90°，得到Gmax-Gmin值如圖3所示。

圖3 陣列增益最大值與最小值之差變化 趨勢(φJ=5°,φs=10°～90°)Fig.3 Difference between the maximum and minimum values of the array gain(φJ=5°,φs=10°～90°)

上述數值計算中干擾信號俯仰角φs保持不變，現令干擾俯仰角φJ從1°遍歷至15°，由于得到的圖像較多，這里不一一列出，僅給出干擾俯仰角為1°、10°和15°時的圖像作為示例，如圖4所示。

(a)φJ=1°

(b)φJ=10°

(c)φJ=15°圖4 陣列增益極大值與極小值之差變化趨勢(φs=10°～90°)Fig.4 Difference between the maximum and minimum values of the array gain(φs=10°～90°)

從圖4中可以發現：Gmax-Gmin的變化趨勢完全相同，不同干擾俯仰角下Gmax-Gmin最大值的差異僅有1dB左右，造成這一結果的原因是干擾俯仰角φJ變化范圍較小(僅1°～15°)，因此對陣列增益的取值范圍影響不大。此外，也可以發現，相同信號俯仰角條件下，Gmax-Gmin總是在方位角間隔180°左右取得最大值。綜上，可以得出結論：在信號俯仰角越低、方位角間隔越靠近180°時，陣列旋轉對陣列增益的改善程度越大，也即對PI算法抗干擾性能的提升越大。對于四陣元Y型陣列，在約束干擾來自低仰角、信號來自高仰角時，通過數值計算遍歷所有來波方向可得，陣列旋轉對抗干擾輸出后載噪比的改善理論上最大可以達到14dB左右。

考慮一個位于水平面的天線陣，以一定的角速度在平面內勻速旋轉，干擾源位置固定不變，或者相對天線陣以極小的角速度運動。由于導航衛星相對于地球運動的角速度很小，以GPS為例，GPS衛星運動角速度約0.0084(°)/s，因此在上述條件下可以認為衛星信號和干擾信號相對于旋轉天線陣，其俯仰角在短時間內是不變的，而他們的方位角由于陣列旋轉在[0,2π]內連續變化。

結合以上陣列增益G的性質可知，天線陣旋轉時，方位角θs連續變化，陣列增益G會在Gmax和Gmin之間周期性變化，相比固定天線陣不變的陣列增益G0，由于Gmin≤G0≤Gmax，因此旋轉天線陣能夠在一段時間內獲得更高的陣列增益(最大值附近)，即能夠輸出更高的載噪比，這意味著接收機將獲得更佳的捕獲性能。當然，陣列增益會隨著天線陣旋轉而周期性的變小，但由于導航接收機的跟蹤靈敏度一般比捕獲靈敏度低10dB左右[16]，因此只要信號被成功捕獲并跟蹤，載噪比減小時信號并不會輕易的失鎖；即使信號失鎖，信號失鎖后重捕的難度也遠小于直接捕獲的難度。因此從信號捕獲效果看，陣列旋轉能夠改善接收機的信號捕獲性能。

關于天線陣旋轉角速度，主要考慮2個約束因素，一方面要保證陣列增益在極大值附近時，接收機有足夠的數據實現捕獲跟蹤，因此角速度不能過快；另一方面，旋轉角速度也不能過慢，因為旋轉過慢會導致陣列增益變化緩慢，延長信號捕獲時間。陣列旋轉角速度需要考慮上述2個因素，并結合接收機的實際性能和使用需求進行選擇。

4 實驗驗證

為了驗證理論分析和數值計算的正確性，使用軟件接收機進行仿真。仿真中，天線陣使用四陣元Y型陣列，陣元間距半波長，導航信號使用北斗B3民碼信號，信噪比為-20dB，干擾為20M帶寬的高斯白噪聲干擾，干信比為70dB，天線陣以1(°)/s的角速度進行旋轉。不同的時間段，干擾信號和導航信號隨機選擇不同的來波方向，如表1所示。

表1 干擾信號及導航信號來波方向

經過PI算法抗干擾處理后，實際陣列增益與利用式(22)計算的理論陣列增益對此如圖5所示。

圖5 陣列增益仿真值與理論值對比Fig.5 Comparison of the simulation and the theoretical value of array gain

從圖5可以看出，不同來波方向下，仿真陣列增益均與理論陣列增益保持一致，證明了理論推導的正確性。鑒于理論推導和數值計算僅分析了單干擾的情況，利用仿真研究了多干擾條件下陣列增益隨陣列旋轉的變化規律。

對于雙干擾情況，假設環境中存在一個GNSS信號，信噪比為-20dB，還存在一個高斯寬帶干擾和一個連續波干擾，干信比均為70dB，天線陣以1(°)/s的角速度旋轉。不同的時間段，干擾信號和導航信號隨機選擇不同的來波方向，如表2所示。

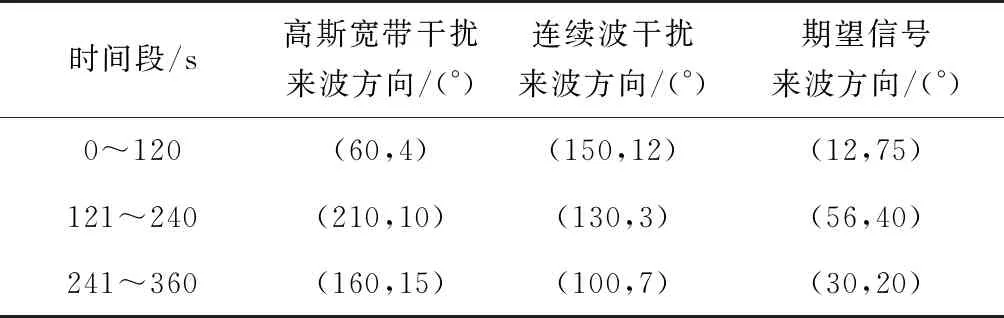
表2 雙干擾條件下信號來波方向

經過PI算法抗干擾處理后，陣列增益的仿真結果如圖6所示。

圖6 雙干擾存在條件下的陣列增益Fig.6 Array gain in the presence of two interfering signals

從圖6可以看出，雙干擾存在條件下，陣列增益變化曲線與單干擾條件下的變化曲線明顯不同。例如雙干擾條件下，增益變化曲線的極值點與最大值和最小值點并不一定重合；其次，對于不同的來波方向，曲線的變化形式也有較大的差異。但可以發現，隨著陣列旋轉，陣列增益仍然以60°為周期在最大值和最小值之間連續變化，在不同的時段，陣列增益的最大值與最小值之差分別為15dB、5dB和2dB。

在雙干擾仿真的基礎上，增加一個高斯窄帶干擾，使仿真環境中存在3個干擾。不同的時間段，干擾信號和期望信號的來波方向，如表3所示。

表3 三干擾條件下信號來波方向

經過PI算法抗干擾處理后，陣列增益的仿真結果如圖7所示。

圖7 三干擾存在條件下的陣列增益Fig.7 Array gain in the presence of three interfering signals

從圖7可以看出，三干擾條件下，陣列增益仍然以60°為周期在最大值和最小值之間連續變化，在不同時段，陣列增益的最大與最小值之差分別為4dB、5dB和14dB。

以上仿真結果說明，在存在多干擾條件下，旋轉天線陣仍然可以改善陣列對衛星信號的增益，提升抗干擾輸出后的載噪比。

5 結論

本文以陣列天線接收機中常用的PI算法為研究對象，通過理論推導的方法研究了信號來波方向與陣列增益的關系，并在此基礎上分析了陣列增益隨陣列旋轉的變化規律。分析結果表明，PI算法下陣列增益受到干擾和導航信號來波方向的影響，相比于固定天線陣，陣列旋轉可提升陣列增益，意味著陣列旋轉可改善輸出載噪比，并提升接收機捕獲性能。仿真結果證明了理論和數值分析的正確性，并進一步證明了在多干擾存在的條件下，陣列旋轉仍可得到相似結論。該研究成果對設計更高性能的衛星導航功率倒置陣具有一定的參考及借鑒價值。