改進Dijkstra算法在大型城市軌道交通網計價系統中的應用*
謝建平,陳治亞,鄧連波,謝宜斌,楊 坤
(1.中南大學 交通運輸工程學院,湖南 長沙 410075;2.長沙市軌道交通集團有限公司,湖南 長沙 410133)
隨著城市地鐵建設的迅猛發展,國內外眾多城市地鐵線路均已達到網絡化運營規模。這將使得兩個站點間存在多條行走路徑,以哪條路徑作為計價路徑,才能確保其計價的科學性、合理性,是當前軌道交通行業研究的熱點課題之一。
針對地鐵兩個站點間距離的長短對軌道交通計價的影響,國內外許多專家學者對此進行了深入的研究。文獻[1]通過構建城市客運系統整體出行時間最小的雙層規劃模型,研究了城市軌道交通系統在城市客運結構中的作用。文獻[2-6]通過建立模型對票價策略進行了優化,但未對軌道交通成網后各車站間票價計算方式進行深入探討。文獻[7-18]分別就節點約束型、改進的Dijkstra算法的最短路程計算,基于結合 Dijkstra算法的信息素遞減蟻群( Dijkstra and Ant Colony Optimization based on Pheromone Declining,Dijkstra-PD-ACO)算法的大城市公交線路優化等方面進行研究和探討,而對于Dijkstra算法優化,并將其應用于城市軌道交通各車站票價計算方面未做詳細且深入的研究。文獻[19-20]通過建立兩種定價方式的雙層規劃模型對影響票價的因素進行研究,研究結果表明對價格的敏感度是影響兩種定價的主要因素。
盡管有眾多的專家學者針對Dijkstra算法在大型城市軌道交通線網計價系統中的應用進行了深入研究,但是到目前為止,對Dijkstra算法進行改進并將其應用在大型城市軌道交通線網計價系統中的研究很少。因此,對Dijkstra算法進行改進并將其應用在大型城市軌道交通線網計價系統中具有非常重要的意義。本文對傳統的Dijkstra算法進行了改進,使用傳統的Dijkstra算法和改進的Dijkstra算法計算分析了長沙地鐵罐子嶺站至毛竹塘站間的最短距離,并對結果進行了分析。為進一步研究Dijkstra算法在大型城市軌道交通線網計價系統中的應用提供了參考。
1 改進Dijkstra算法的實現
1.1 改進Dijkstra算法的主要思想
本算法主要根據地鐵線網規劃、建設規劃、線路里程表等相關資料,提取線網各車站的里程標,繪制出地鐵線網示意圖,再篩選出線網所有換乘站,且對于同一線路中兩換乘站之間無其他換乘站可認定為相鄰換乘站。根據換乘站之間的關系及換乘站的中心線里程標,使用傳統的Dijkstra算法計算各換乘站之間的最短距離。算法詳細思路如圖1所示。
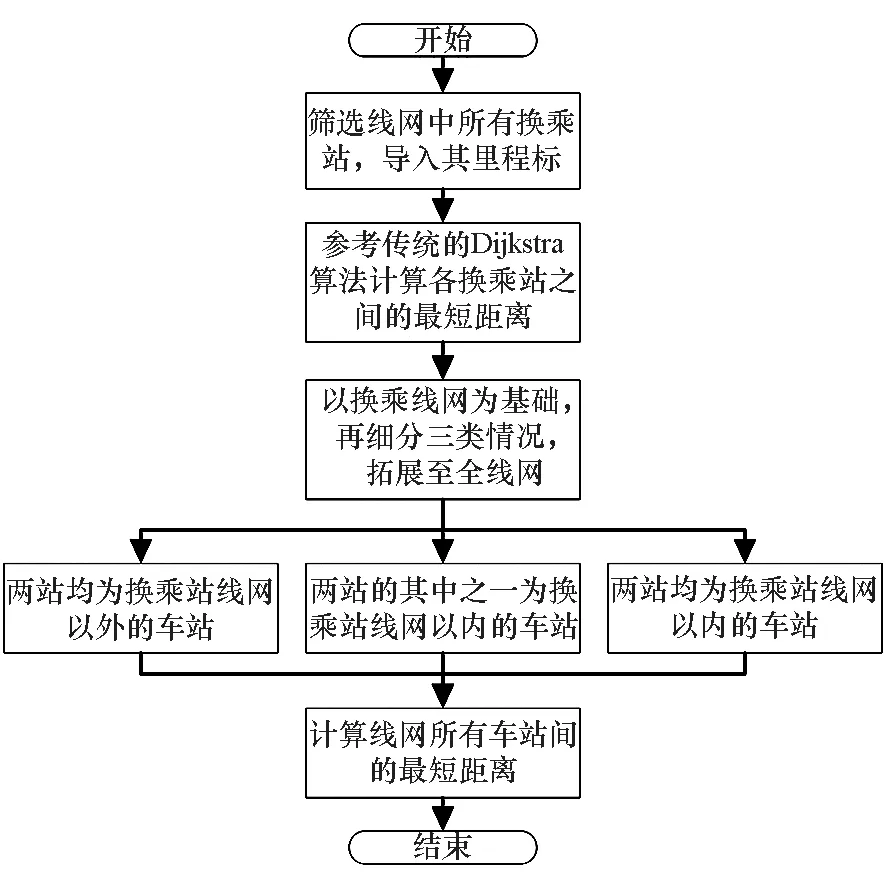
圖1 改進Dijkstra算法流程圖Fig.1 Improved Dijkstra algorithm flow chart
1.2 傳統的Dijkstra算法計算換乘站間最短距離
假定地鐵線網有n個換乘站,首先參照傳統的Dijkstra算法計算出線網所有換乘站之間的最短距離,算法實現如圖2所示。
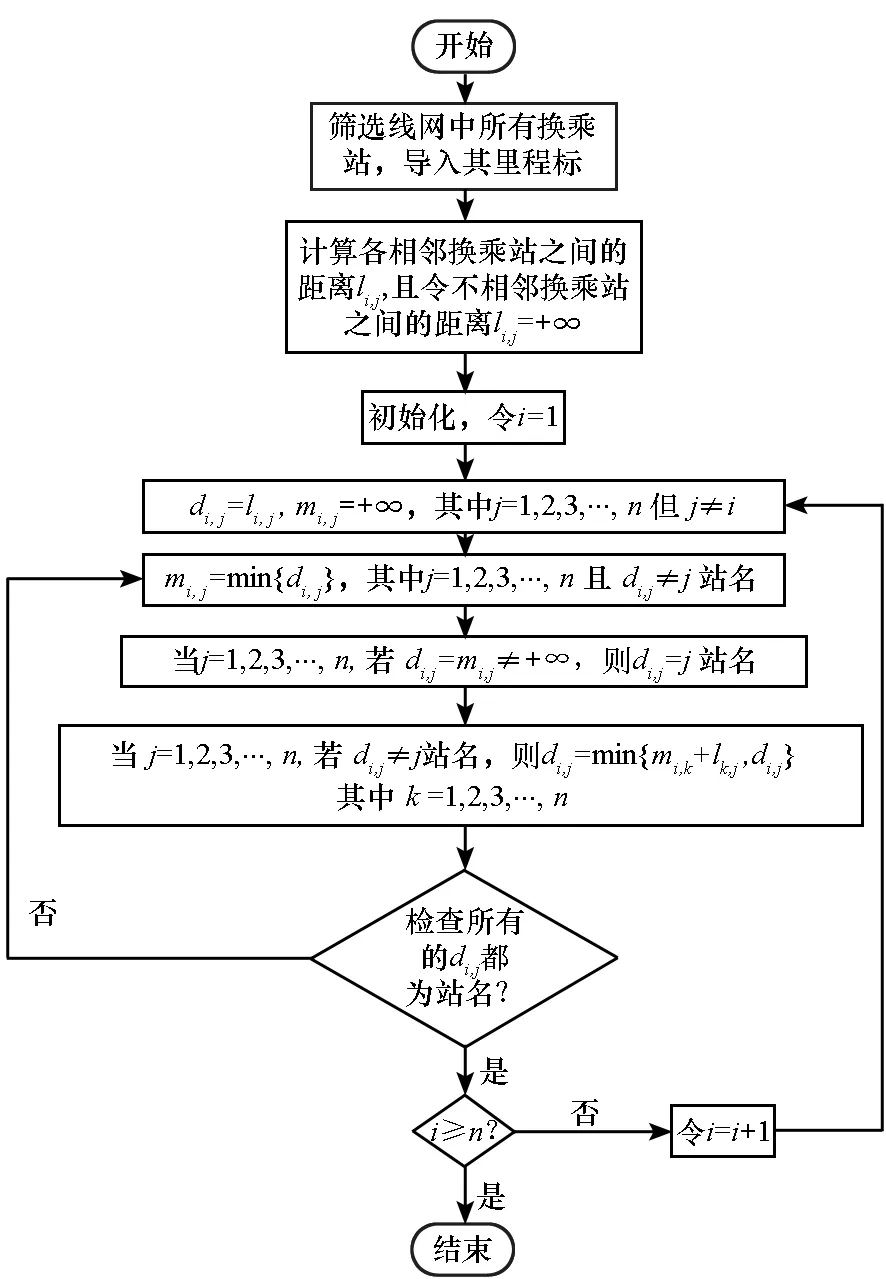
圖2 傳統的Dijkstra算法計算換乘站間最短距離流程圖Fig.2 Traditional Dijkstra algorithm to calculate the shortest distance flow chart between transfer stations
算法詳細描述如下:
Step1:篩選出線網中所有換乘站,導入其里程標。
Step2:計算所有相鄰換乘站之間的距離li,j,令本站的li,i=0且不相鄰換乘站之間的距離li,j=+∞,其中i=1,2,3,…,n。
Step3:初始化,令i=1。
Step4:初始化,令di,j=li,j,mi,j=+∞,其中j=1,2,3,…,n且j≠i。
Step5:比較所有新解且不為站名的di,j大小,即令mi,j=min{di,j},其中j=1,2,3,…,n且di,j≠j站名。
Step6:對于所有j=1,2,3,…,n,當di,j=mi,j≠+∞時,則令di,j=j站名。
Step7:對于所有j=1,2,3,…,n,若di,j≠j站名,則令di,j=min{mi,k+lk,j,di,j},其中k=1,2,3,…,n。
Step8:檢查是否所有j的di,j=j站名,其中j=1,2,3,…,n,若為否,則跳至Step 5,若為是,則跳至下一步。
Step9:檢查i是否大于等于n,若為否,則令i=i+1且跳至Step 4,若為是,則該算法結束。
其中:i,j表示換乘站線網中第i或j個換乘站;n表示換乘站線網總計有n個換乘站;li,j表示兩相鄰換乘站i和j之間的距離,若不相鄰,其取值為+∞;mi,j表示換乘站i與換乘站j之間的最短距離;di,j表示換乘站i與換乘站j之間的最短距離求值過程中經歷的中間值。
1.3 改進的Dijkstra算法計算線網各車站間最短距離
參考如上算法,計算出各換乘站之間最短距離表,再參考圖2流程圖中算法的主要思想,細分三個部分對線路各車站間最短距離進行計算,其具體的算法實現如圖3所示。
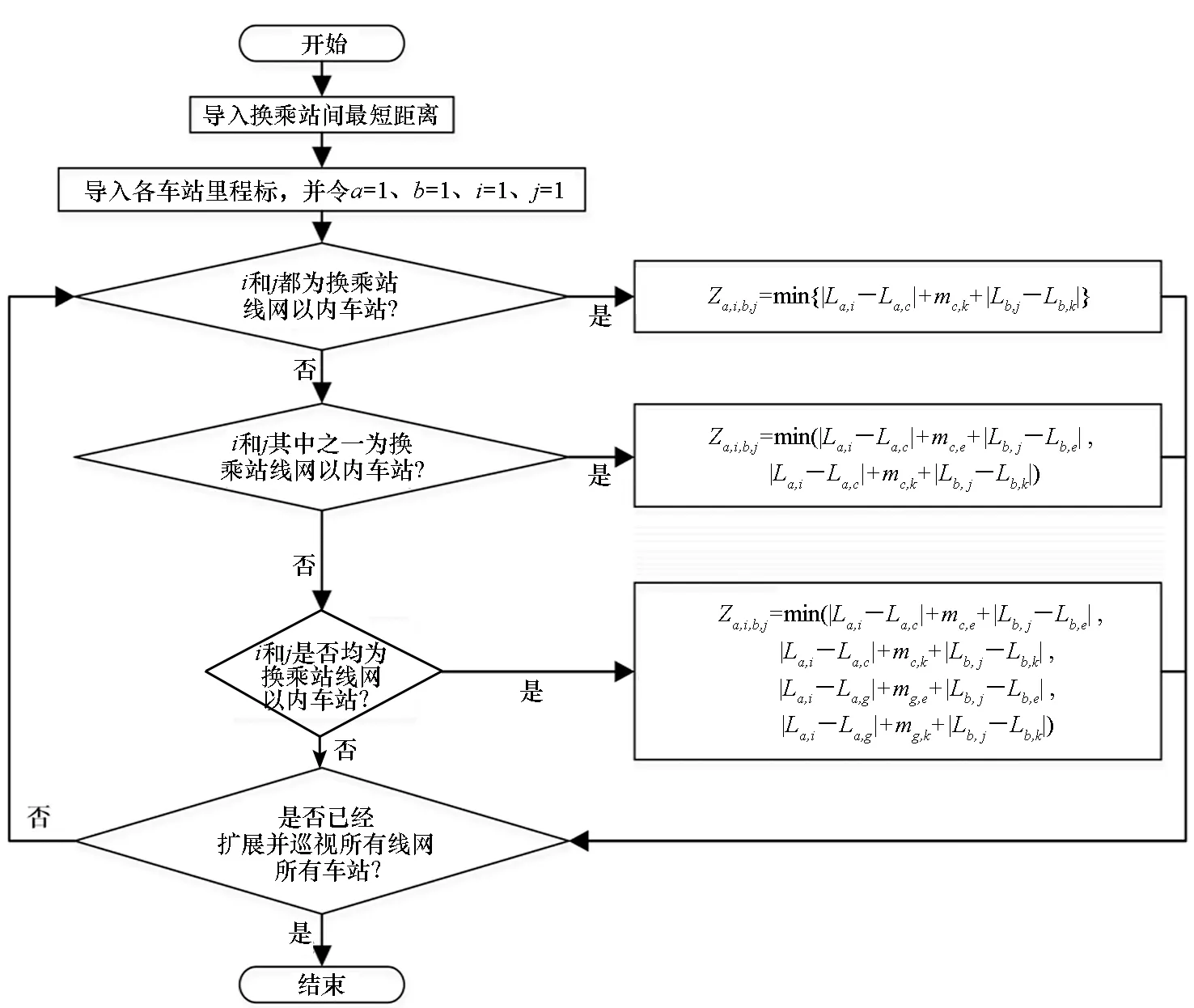
圖3 改進的Dijkstra算法計算換乘站間最短距離流程圖Fig.3 Flow chart which used the improved Dijkstra algorithm to calculate the shortest distance between the stations
算法詳細描述如下:
Step1:導入換乘站間的最短距離即圖2算法的結果,并參考換乘站在線網中的實際位置對算法結果進行適當的調整。
Step2:導入線網中各車站的線路里程標,并令a=1、b=1、i=1、j=1。
Step3:檢查i和j是否為換乘站線網以內的車站,若為否,則跳至下一步,若為是,則令:
Za,i,b,j=min{|La,i-La,c|+mc,k+|Lb,j-Lb,k|}
(1)
Step4:檢查i和j其中之一是否為換乘站線網以內的車站,若為否,則跳至下一步,若為是,則令:
Za,i,b,j=min(|La,i-La,c|+mc,e+|Lb,j-Lb,e|,
|La,i-La,c|+mc,k+|Lb,j-Lb,k|)
(2)
Step5:檢查i和j是否均為換乘站線網以內的車站,若為否,則跳至下一步,若為是,則令:
Za,i,b,j=min(|La,i-La,c|+mc,e+|Lb,j-Lb,e|,
|La,i-La,c|+mc,k+|Lb,j-Lb,k|,
|La,i-La,g|+mg,e+|Lb,j-Lb,e|,
|La,i-La,g|+mg,k+|Lb,j-Lb,k|)
(3)
Step6:判斷是否已經擴展并巡視所有線網所有車站,若為否,則跳至Step 3,若為是,則該算法結束。
其中:a、b表示線路編號,當算法巡視所有車站時,a和b均等于線路總數;i表示第a條線路中第i個車站,i不大于第a條線路車站總數;j表示第b條線路中第j個車站,j不大于第b條線路車站總數;La,i表示線路a中第i個車站的中心線里程標;Lb,j表示線路b中第j個車站的中心線里程標;Za,i,b,j表示第a條線路中第i個車站與第b條線路中第j個車站的最短距離;c、g表示為圖3中離線路a第i個車站最近的換乘站,是線路a上的第c和g個車站;e、k表示為圖3中離線路b第j個車站最近的換乘站,是線路b上的第e和k個車站;mc,e、mc,k表示換乘站c與換乘站e或k的最短距離,是根據圖2算法求出的結果。
1.4 線網各車站間票價計算算法
根據圖3中算法求出線網各車站之間最短距離Za,i,b,j,再參考如圖4所示算法,核算線網各車站之間的票價。

圖4 線網各車站間票價計算算法Fig.4 Algorithm flow chart of ticket price between stations in line network
算法詳細描述如下:
Step1:導入線網各車站間最短距離Za,i,b,j,即圖3的計算結果。
Step2:初始化,令p1=0,F、Pa,i,b,j均為+∞,f1=0。
Step3:初始化,令m=1。
Step4:判斷第a條線路第i個車站與第b條線路第j個車站之間的最短距離Za,i,b,j是否等于p1,即Za,i,b,j=p1,若為是,則跳至Step 6,若為否,則跳至Step 5。
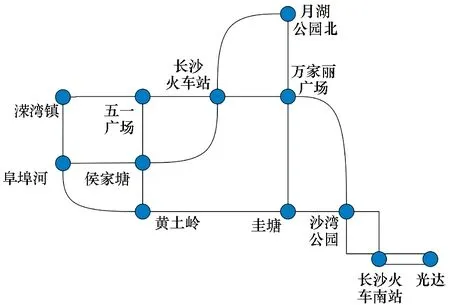
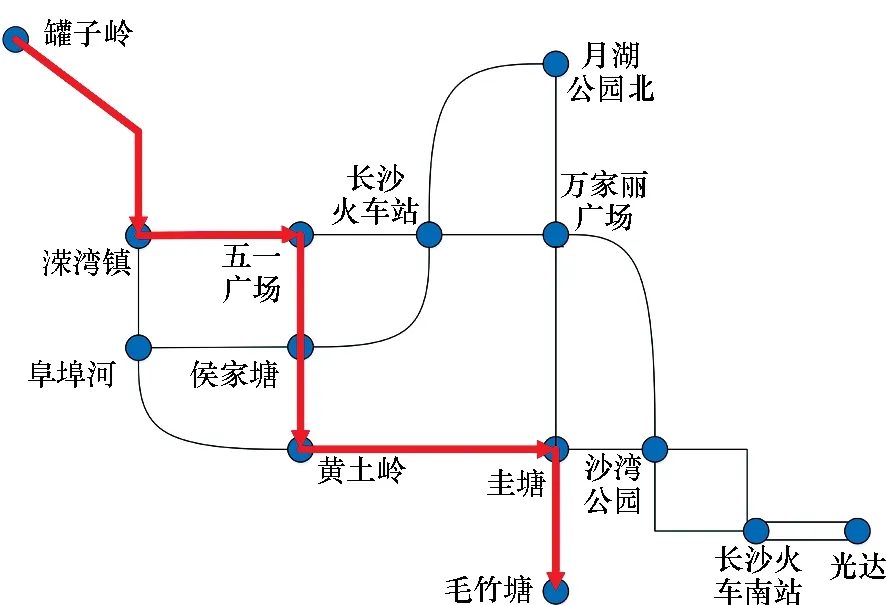
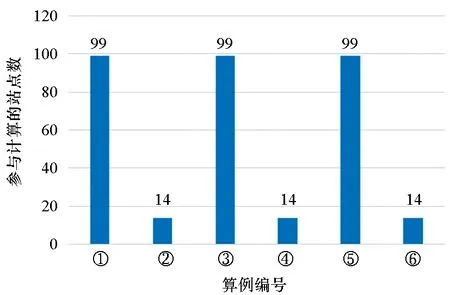
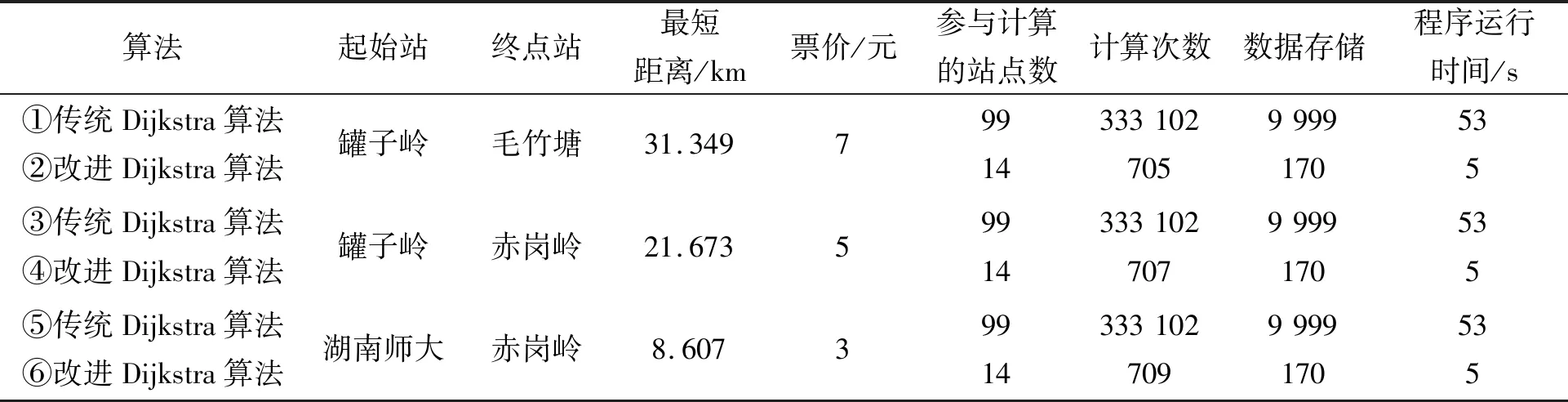
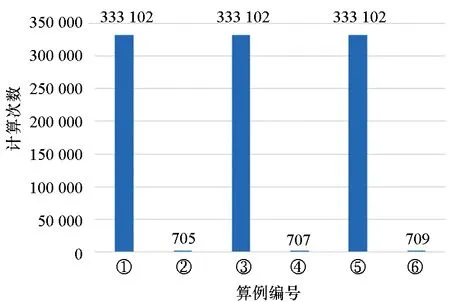
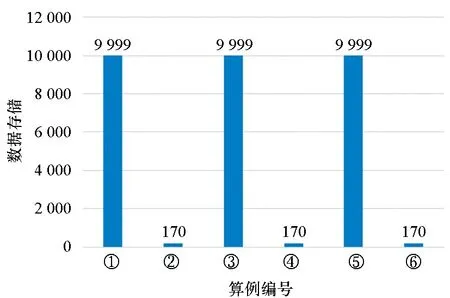
Step5:判斷第a條線路第i個車站與第b條線路第j個車站之間的最短距離Za,i,b,j屬于哪個計價區間,即檢查pm Step7:檢查所有Pa,i,b,j是否不等于+∞,即Pa,i,b,j≠+∞,若為否,則跳至Step 3,若為是,則該算法結束。 其中:m表示城市地鐵第m個計價區間;pm表示在第m個計價區間乘客可乘坐的距離,F表示城市地鐵起步票價;Pa,i,b,j表示第a條線路中第i個車站與第b條線路中第j個車站的票價,fm表示第m個計價區間較第m-1個計價區間需要調整的票價。 以長沙地鐵罐子嶺站至毛竹塘站、罐子嶺站至赤崗嶺站、湖南師大站至赤崗嶺站的最短距離計算為例。對于傳統算法需要根據長沙地鐵1~5號線線網布局及各車站的中心線里程標,計算線網中各相鄰車站之間的距離,以罐子嶺站(或湖南師大站)為目標節點,并建立集合1,開始遍歷長沙地鐵1~5號線線網各車站,逐步將計算出最短距離的車站納入集合1,算法在完成長沙地鐵線網99個車站間最短距離的計算后結束,并根據要求提取出罐子嶺站至毛竹塘站(或罐子嶺站至赤崗嶺站,或湖南師大站至赤崗嶺站)的最短距離。改進的Dijkstra算法需根據長沙地鐵1~5號線線網布局及各車站里程標,將線路中換乘站篩選出來,根據長沙地鐵1~5號線線網布局,共計有12個換乘站,若任意兩個換乘站在同一線路且其之間無其他換乘站,則認定其為相鄰換乘站,將相鄰換乘站連接起來,形成換乘站線網(如圖5所示),并計算相鄰換乘站之間的距離;再根據傳統Dijkstra算法,計算各換乘站之間最短距離,而長沙地鐵的換乘站線網圖只有12個換乘站,較線網99個車站,計算難度及消耗時間大大縮減;再詳細按照圖3將線網各車站細分為三類,計算罐子嶺站至毛竹塘站、罐子嶺站至赤崗嶺站,湖南師大站至赤崗嶺站的最短距離,如罐子嶺站和毛竹塘站均為換乘站線網以外的車站,則罐子嶺站至毛竹塘站的計算方法可參考圖3中第一種情況,對于罐子嶺站至赤崗嶺站而言,其中赤崗嶺站為換乘站線網以內車站,則罐子嶺站至赤崗嶺站的計算方法可參考圖3中第二種情況,湖南師大站和赤崗嶺站均為換乘站線網以內車站,則湖南師大站至赤崗嶺站的計算方法可參考圖3中第三種情況。圖6和圖7以罐子嶺站至毛竹塘站為例,使用兩種算法時所涉及的站點及最短距離行走路徑標記如下所示。 圖5 長沙地鐵1~5號線換乘站線網圖Fig.5 Transfer station network of Changsha metro line 1~5 圖6 傳統Dijkstra算法計算罐子嶺站至毛竹塘站最短距離時行走路徑Fig.6 Traditional Dijkstra algorithm to calculate the shortest walking path between Guanziling station and Maozhutang station 由圖6和圖7可知,使用傳統Dijkstra算法計算罐子嶺站至毛竹塘站間最短距離時,參與計算的站點數為99,使用改進的Dijkstra算法計算罐子嶺站至毛竹塘站間最短距離時,參與計算的站點數為14。具體情況如表1和圖8~10所示,圖中①~⑥與表1中標號相對應。 圖7 改進Dijkstra算法計算罐子嶺站至毛竹塘站最短距離時行走路徑Fig.7 Improved Dijkstra algorithm to calculate the shortest walking path between Guanziling station and Maozhutang station 圖8 參與計算的站點數比較圖Fig.8 Comparison chart of the number of stations participating in calculation 由表1可知,傳統Dijkstra算法與改進的Dijkstra算法的行走路徑和最短距離大致相同,但在參與計算的站點數、計算次數、數據存儲及運行時間方面,改進的Dijkstra算法都進行了大量縮減。 表1 傳統Dijkstra算法和改進Dijkstra算法的算例比較Tab.1 Example compared with traditional Dijkstra algorithm and improved Dijkstra algorithm 注:目前長沙地鐵票價政策是“起步價2元可乘坐6 km(含6 km),超過6 km采用‘遞遠遞減’的計價原則,6~16 km(含16 km)范圍每遞增5 km加1元,16~30 km(含30 km)范圍內每遞增7 km加1元,30 km以上每遞增9 km加1元”,參考表1可知,罐子嶺站至毛竹塘站的最短距離為31.349 km,屬于30 km以上范圍,票價為7元,罐子嶺站至赤崗嶺站的最短距離為21.673 km,屬于16~23 km(含23 km)范圍,票價為5元,湖南師大站至赤崗嶺站的最短距離為8.607 km,屬于6~11 km(含11 km)范圍,票價為3元。 圖9 計算次數比較圖Fig.9 Comparison chart of calculation times 圖10 數據存儲比較圖Fig.10 Data storage comparison chart 當使用傳統Dijkstra算法和改進的Dijkstra算法求任意兩車站之間最短距離時,所需參與計算的站點數、計算次數及數據存儲比較如表2所示。 表2 傳統Dijkstra算法和改進Dijkstra算法比較Tab.2 Comparison between original Dijkstra algorithm and improved Dijkstra algorithm 表2中,S為地鐵線網站點總數;n為地鐵線網中換乘站總數;x為已經尋找出最短路徑的站點,初始值為1;t為固定參數值,當兩車站均為換乘站線網(含換乘站)以外車站時t取1,其中之一為換乘站線網以內車站時t取3,兩個均為換乘站線網(含換乘站)以內車站時t取5。 在計算過程中,使用傳統Dijkstra算法計算某兩個站點的最短距離時,就需要先根據里程表計算各站點之間的距離初始值,相鄰站點之間的距離為|La,i-La,i+1|,非相鄰車站之間的距離為+∞,其計算次數為S2。而改進的算法中,需要先篩選相應換乘站,并根據換乘站之間的關系,求出各換乘站之間的距離初始值,其計算次數為n2。 在計算過程中,傳統的Dijkstra算法需要的第一個數組,大小為S2,存儲所有車站的初始距離值,并可以用來存儲計算中間值;第一個數組,大小為S,存儲起點至所有車站的最短距離;第三個數組,大小為S,存儲所有節點里程標。而改進的Dijkstra算法,需要存儲的換乘站數組及參與計算車站里程表的數組總數為n2+2n+2,此外,還需要一個變量存儲起點至要求節點的最短距離。 以長沙地鐵1號線北延線一期為例,假定La,i表示線路a中第i個車站的中心線里程標,Lb,j表示線路b中第j個車站的中心線里程標,使用改進Dijkstra算法求解如下: Step1:當i,j均為1號線北延線一期車站,則最短距離Z1,i,1,j=|L1,i-L1,j|。 Step2:當i或j之一為1號線北延線一期車站,假定i為1號線北延線一期車站,則最短距離Z1,i,b,j=|L1,i-L1,1|+Z1,1,b,j,由于i車站為1號線北延線一期車站,離其最近的車站為1號線第1個車站。 Step3:當i和j均非1號線北延線一期車站,則最短距離Za,i,b,j=Za,i,b,j。 算法實例如表3所示。 表3 改進的Dijkstra算法的延展性算例Tab.3 Example of extension of improved Dijkstra algorithm 由于長沙地鐵1號線北延線為1號線新增車站,若按照傳統的Dijkstra算法的原理計算線網中所有車站(含新增車站)間最短距離,需遍歷線網所有車站進行求解,計算煩瑣性增加,顯然其延展性較改進的Dijkstra算法差。 1)改進后的Dijkstra算法克服了傳統算法時間冗長的缺陷,創新地將換乘站從線網中獨立出來,再通過換乘站線網拓展至線網各站,實際中,換乘站數量遠遠小于線網車站總數,這就減少了節點遍歷數和查詢時間,增強了設計的可行性; 2)若需知道線網各車站間最短距離,無須逐一核算各相鄰車站之間的距離,減少了產生誤差的可能性; 3)在換乘站不變,但有新線開通時,只需將車站里程標導入,便可直接計算出該站至其他車站的最短距離,可延展性更強。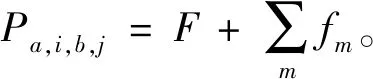
2 改進Dijkstra算法實例與分析
2.1 算法實例

2.2 比較分析

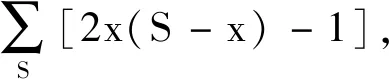
2.3 算法延展

3 結論

