輪式移動機器人滑模軌跡跟蹤控制*
靳宇星
(新疆交通職業技術學院,新疆 烏魯木齊 830001)
隨著人工智能在21 世紀的飛速發展,越來越多的智能化機器人開始在各行各業中被應用,代替人類完成一些具有重復性、危險性的工作。其中輪式移動機器人,因其操作方便、便于運輸和攜帶等優點在海底探測、抗震救災、礦井勘探等領域具有廣泛的應用[1]。由于其長期工作在條件較差、環境因素多變的工況下,因此對其控制性能的可靠性有較高的要求,對其控制策略的研究也一直是中外學者研究的熱門話題。
輪式移動機器人傳統的控制策略主要有PID 控制[2]、模糊控制[3]、反演控制[4]、非線性狀態反饋控制[5]等控制策略。其中PID 控制因其算法簡單易于實現等特點在工業應用中廣泛存在,也是目前移動機器人應用最多的控制策略,但這種線性控制方法,在處理欠驅動問題時往往會出現響應不夠快速、抗干擾能力弱的問題。因此后面的學者都將目光轉向了非線性的控制策略,如滑模控制、模型預測控制等。其中滑模變結構控制具有響應快速、抗干擾能力強、對系統參數依賴性小的優點,被廣泛應用在控制器的設計中,本文選取滑模控制來設計系統的控制律。
1 輪式移動機器人建模
輪式機器人的結構為前后各兩個輪子,兩個后輪是驅動輪為機器人本體提供動力來源,兩個前輪為從動輪,為機器人本體提供支撐作用[6]。驅動輪各有一個電機,用來提供動力,當兩個電機轉速一致時實現前后運動,當兩個電機轉速存在偏差時,由于“差速”的存在從而實現機器人的轉彎運動。在二維平面下其運行軌跡如圖1 所示。
圖1 中,X、Y代表二維平面的坐標軸,x0、y0表示移動機器人的初始位置,xd、yd表示移動機器人的給定參考位置,M為其質心位置。為了更加清晰地分析其運動軌跡,通過數學建模的方法建立其坐標軸下的數學模型。
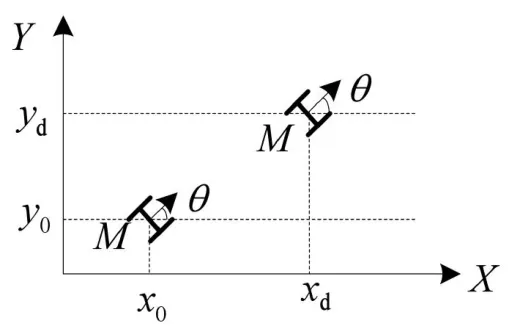
圖1 輪式移動機器人的運動軌跡圖
假設移動機器人的質心與其幾何中心在同一點上,選取相量P=[x,y,θ]T,其中x、y分別表示機器人在X、Y軸方向的位置,θ為機器人前方向同X軸方向的夾角。選取相量W=[v,m]T,其中v、m分別表示機器人的線速度和角速度作為運動學模型的輸入。由此可以將移動機器人建模如下:
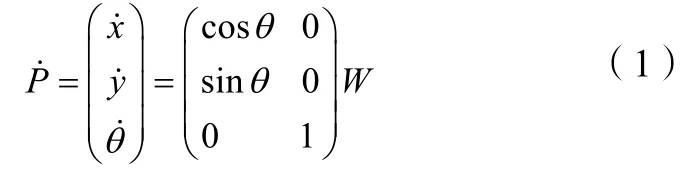
為了確保控制系統準確可靠,本文采用內外環的結構,將系統分為了位置子系統(外環)和姿態子系統(內環)的結構來分別設計控制律,系統的整體控制結構如圖2 所示。
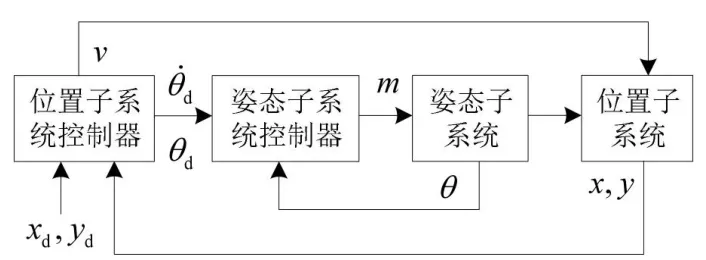
圖2 基于內外環結構的控制系統框圖
2 輪式移動機器人位置控制律設計
位置控制律的設計目標是使得移動機器人在二維平面的X、Y軸方向能夠快速地到達給定參考點。通過設計的位置控制律,實現X、Y軸方向準確及時的跟蹤,并保證前進角度θ的穩定。
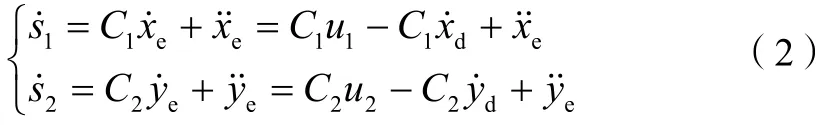
則可由此設計控制律為:
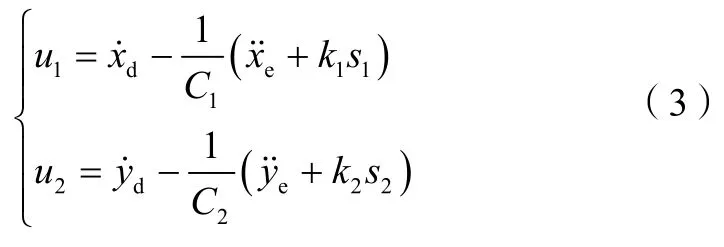
根據李亞普洛夫方程可以驗證系統是穩定的,跟蹤誤差呈指數形式收斂于0。
由vcosθ=u1、vsinθ=u2可得u1/u2=tanθ,可以看出系統機器人的前進角θ取值范圍為(-90°,90°)。則可以得到滿足理想跟蹤軌跡的θ值為θ=arctan(u1/u2)。該角度值即為滿足控制律式(3)所需要的角度。
在實際運行過程中這一角度無法滿足與給定角度值完全一致,尤其在控制初始階段,具有較大的偏差,可能會造成系統不穩定,因此在位置系統的輸出時刻將所求得的角度θ當成給定的理想值作為內環姿態控制律的輸入。為了保證系統的穩定性和跟蹤誤差的收斂性,在姿態子系統中設計控制的律時應當使其收斂速度大于位置子系統。
3 輪式移動機器人姿態控制律設計
通過位置控制律的設計實現了對位置方向的跟蹤,并獲得了滿足給定位置點的跟蹤角度θd,此時需要對系統的姿態也采用滑模控制算法實現θ跟蹤到θd。
同樣選取θ的跟蹤誤差θe=θ-θd,選取滑模函數為則有:
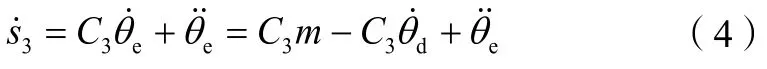
為了確保其誤差收斂速度大于位置子系統,可以選取收斂速度較快的指數趨近律來設計,并采用飽和函數代替開關函數以減小滑模控制中產生的抖振現象。則可由此設計控制律為:
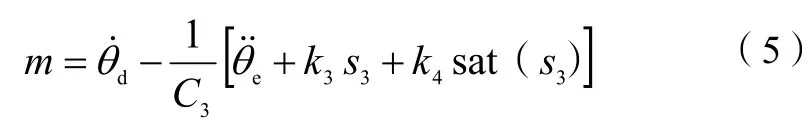
同樣可根據李亞普洛夫方程驗證系統是穩定的,姿態誤差呈指數形式快速收斂為0。
4 仿真實驗
為驗證本文設計的正確性,本文在MATLAB 仿真軟件下搭建了輪式移動機器人的仿真模型進行仿真驗證。運行過程中給定相關的仿真參數如下。
位置指令[xd,yd]T=[t,sin(2x)+x+1]T,取控制器參數C1=C1=C1=0.1,k1=k2=0.2,k3=3,k4=2。移動機器人初始位置位于[0,0,0]。
仿真實驗的目標是通過姿態控制器和位置控制器,使得移動機器人能夠在短時間內從初始位置以最小的誤差跟蹤到給定的參考點,并能夠保證穩定運行,圖3、圖4 給出了系統運行30 s 時間后,相應的被控對象的輸出響應曲線。
圖3 給出了移動機器人在仿真軟件中的二維平面軌跡跟蹤曲線,虛線代表期望的移動軌跡,實線代表機器人實際的運行軌跡。由圖3 可以看出,在仿真開始階段機器人運行軌跡同期望值存在偏差并在逐步縮小,到仿真進行至10 s之后,機器人運行軌跡同期望軌跡完全一致,說明系統能夠滿足控制要求。
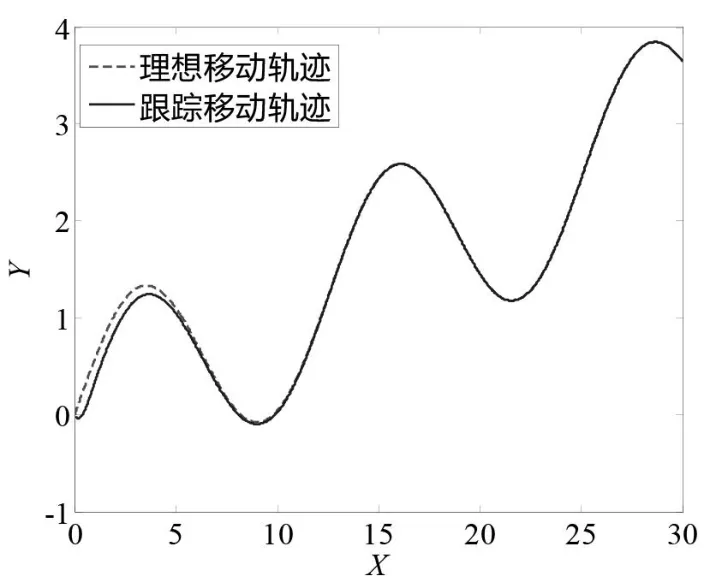
圖3 移動機器人在二維平面的軌跡跟蹤仿真圖
圖4 給出了移動機器人在仿真軟件中的x、y和θ的跟蹤曲線,由圖4 可以看出所設計的位置控制器和姿態控制器控制器能夠快速準確地跟蹤上兩個位置方向和一個角度方向的自由移動軌跡,確保系統穩定運行。
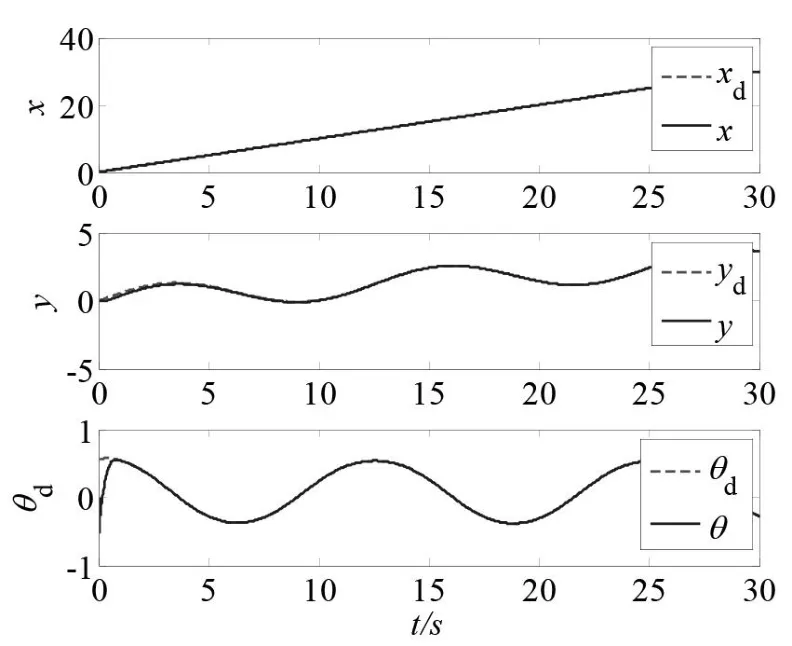
圖4 移動機器人在位置和角度的軌跡跟蹤仿真圖
5 結論
本文針對輪式移動機器人軌跡跟蹤系統,采用滑模控制技術,將被控系統分為姿態子系統和位置子系統的機構分別設計了相應的滑模控器,實現了輪式移動機器人在二維平面的軌跡跟蹤控制,具有控制響應速度快、精確性高的特點。最后進行仿真實驗,驗證了設計的正確性和可靠性。

