受特定變化趨勢限制的傳感器數據處理方法研究

周俊華，雷孟飛，梁曉東

（湖南聯智科技股份有限公司，湖南 長沙 410000）

0 引 言

在物聯網傳感技術領域，經常需要用到各種各樣的傳感器對物理世界進行感知，傳感器的一般原理是將現實世界的物理量通過各種手段變為電學量，通過標定物理量和電學量之間的對應關系后，則可以通過測量電學量的值反推出被測物理量。

現實世界中的很多物理量在一定的條件限制下，具有限定的變化趨勢，如隨著時間的變化，松軟地面的沉降呈現出遞增趨勢，混合液體中易揮發組分的含量會呈現遞減趨勢。對于這些具有明確呈遞增或遞減變化趨勢的物理量，其真實值只有可能在變化趨勢內單向變化，而因傳感器的原理及其精度等因素的制約，會出現部分測量的原始數據不符合已知的變化趨勢的問題，這種明顯的錯誤在數據展示的時候是不能出現的。

常用的處理方法為通過多個同類型的傳感器一起測量，然后采用數據融合的算法得到融合結果[1]，但是目前針對不同信息的融合算法仍然缺乏合適的評價體系[2]；另外基于成本考慮，單傳感器的系統目前仍然在大量采用[3]；廣大學者對單傳感器的數據處理方法也進行了很多研究，一般的處理技術可分為基于統計、基于最近鄰、基于聚類等方法[4]；另外也可基于傳感器的系統誤差原理，通過濾波的方式進行處理[5]，比如曾金芳提出了基于最大熵方法的數據處理[3]，宋強提出了極大似然法的數據處理等[6]。

筆者認為對于該類原始數據，其處理具有一定的特殊性。由于事物的“真值”是不可得的，只能通過不斷地提高測量精度逼近，所以對于傳感器所測量的每一個原始數據，都不能隨意地篡改或者剔除，更不能簡單地采用擬合或者其他的算法對整個原始數據做替換處理。本文基于可信傳感器測量得到的每一個數據，以及使曲線符合限定的變化趨勢的原則提出一種數據處理方法，該方法能夠通過剔除最少的數據個數來滿足上述需求。

1 傳感器數據處理算法

1.1 選定數據處理窗口，根據限定趨勢找出問題數據點

在原始數據中選取n(n≥3)個連續的原始數據作為一個處理窗口進行數據處理，窗口隨時間依次往后推移，最終實現對所有數據的處理。

假設處理窗口內原始數據滿足函數關系式Y=F(xi)，其中i=1, 2,...,n,n為處理窗口內原始數據的總數量。找出處理窗口內不符合已知限定變化趨勢的個別原始數據記為問題數據點，且問題數據對應的序號為jk，其中k=1, 2,...,m,m為問題數據的總數量；如果有連續p個數據不符合變化趨勢的則只記錄為一個問題數據點，同時引入參數tk，tk=p-1。

1.2 統計所有剔除問題數據事件的取值

對于序號為jk的問題數據點分別判斷其前后相鄰的原始數據是否符合處理窗口內原始數據的變化趨勢，若在序號為jk的問題數據之前相鄰的原始數據有不符合的，記為事件Jk1并統計事件包含的問題數據個數，若在序號為jk的問題數據之后相鄰的原始數據有不符合的，記為事件并統計事件包含的問題數據個數。

變化趨勢受限定則說明數據滿足呈遞增變化趨勢或遞減變化趨勢，遞增量（即后一個大數減去前一個小數的值）或遞減量（即前一個大數減去后一個小數的值）大于等于0。

（1）若處理窗口內的原始數據的變化趨勢為遞增變化趨勢，則：

如果F(xj)≥F(xj-2)，則處理窗口內序號jk之前的原始數據已經符合遞增變化趨勢，事件Jk1包含的問題數據個數為剔除的數據數量加上tk。

如果F(xj)＜F(xj-2)，取jk=jk-1，若jk-1＞jk-2，則返回步驟①；若jk-1≤jk-2，則結束，刪除小于等于jk且大于jk-1之間的所有數據。

如果F(xj+1)≥F(xj-1)，則處理窗口內序號jk之后且序號jk+1之前的原始數據已經符合遞增變化趨勢，事件包含的問題數據個數為剔除的數據數量。

如果F(xj+1)＜F(xj-1)，取jk=jk+1，若jk+1＜jk+1，則返回步驟①；若jk+1≥jk+1，則結束，刪除大于等于jk且小于jk+1之間的所有數據。

（2）若處理窗口內的原始數據的變化趨勢為遞減變化趨勢，則：

①對于Jk1事件，具體是：剔除序號為jk-1的問題數據；判斷序號為jk-2的原始數據Y=F(xj-2)與序號為jk原始數據Y=F(xj)的關系。

如果F(xj)≤F(xj-2)，則處理窗口內序號jk之前的原始數據已經符合遞減變化趨勢，事件包含的問題數據個數為剔除的數據數量加上tk；

如果F(xj)＞F(xj-2)，取jk=jk-1，若jk-1＞jk-1，則返回步驟①；若jk-1≤jk-1，則結束，刪除小于等于jk且大于jk-1之間的所有數據。

如果F(xj+1)≤F(xj-1)，則處理窗口內序號jk之后且序號jk+1之前的原始數據已經符合遞減變化趨勢，事件包含的問題數據個數為剔除的數據數量；

如果F(xj+1)＞F(xj-1)，取jk=jk+1，若jk+1＜jk+1，則返回步驟①；若jk+1≥jk+1，則結束，刪除大于等于jk且小于jk+1之間的所有數據。

1.3 選取最優剔除事件的集合

若上述不存在多組A值相等的情況，則所得數據為最終保留數據；若上述存在至少兩組A值相等的情況，則分別記為Ap，p為1, 2,...,q,q為A值相等的總組數。對多組A值相等的數據采用線性方程最小二乘法進行數據擬合，結合偏差平方和來進行輔助判斷，如下：

對原始數據函數Y=F(xi)進行擬合，得到擬合函數Yi=f(xi)=a'xi+b'，其中i=1, 2,...,n，求出a'和b'的值。

比較σ2p值之間的大小，選取數值最小的偏差平方和作為最優解，所述最優解對應的數據剔除方案為最優方案，采用最優方案剔除數據后得到最終保留數據為最佳處理結果。

2 實例驗證

采用激光測距儀測量一處具有沉降趨勢的淤泥堆積場的表面高度變化情況，由于淤泥具有沉降趨勢，所以測量數據應該呈現限定的遞增變化趨勢。原始數據見表1所列。

表1 原始數據表

在原始數據中選取n=24(n≥3)個連續的原始數據作為一個處理窗口進行處理，窗口內不符合原始數據變化趨勢的數據點為j1=7，j2=15和j3=20，且t1=0，t2=0，t3=1。

（1）對于J11事件，剔除序號為j1-1=7-1=6的問題數據之后，判斷序號為j1-2=7-2=5的原始數據Y=F(xj-2)=F(x5)與序號為j1=7的原始數據Y=F(xj)=F(x7)的關系。

因F(x7)≥F(x5)，所以處理窗口內序號j1=7之前的原始數據已經符合遞增變化趨勢，事件包含的問題數據個數為1。

（2）對于J12事件，剔除序號為j1=7的問題數據之后，判斷序號為j1+1=7+1=8的原始數據Y=F(xj+1)=F(x8)與序號為j1-1=7-1=6的原始數據Y=F(xj-1)=F(x6)的關系。

因F(x8)＜F(x6)，所以繼續剔除序號為j1+1=7+1=8的問題數據，判斷序號為j1+2=7+2=9的原始數據Y=F(xj+2)=F(x9)與序號為j1-1=7-1=6的原始數據Y=F(xj-1)=F(x6)的關系。

因F(x9)≥F(x6)，則處理窗口內序號j1=7之后且序號j2=15之前的原始數據已經符合遞增變化趨勢，事件J12包含的問題數據個數為2。

依此類推，分別判斷序號為j2和j3的問題數據的情況，求得 ：J11=1，J12=2，J21=1，J22=1，J31=3，J32=2。

將上述的事件J11，J12，J21，J22，J31和J32包含的問題數據個數按照表達式A=min(J11,J12)+min(J21,J22)+min(J31,J32)=min(J11,J21,J32)=min(J11,J22,J32)=1+1+2=4計算出最少問題數據個數A，得到相應的剔除問題數據最少的方案。由于有兩種方案得到的A值相等，所以繼續進行后續的處理判斷。

對處理窗口內的原始數據采用線性方程最小二乘法進行數據擬合，得到擬合函數Yi=f(xi)=a'xi+b'，其中i=1, 2,..., 24；求出a'=0.133 7和b'=5.378 3。

上述兩組A值相等的情況分別記為。

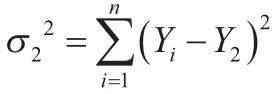
比較σ12和σ22值的大小，選取數值最小的偏差平方和σ22作為最優解，所述最優解對應的數據剔除方案為最優方案，采用最優方案剔除數據后得到最終保留數據為最佳處理結果，如圖1所示。

3 結 語

基于剔除最小數據量的原則進行受特定變化趨勢限制的單傳感器的數據處理，通過采用平滑窗口的方法依次處理所有數據，采用直觀選取不符合變化趨勢的數據并通過窮舉法結合排列組合選出剔除數據量最小的方案，對于存在多種情況得到剔除同樣數據量的方法，則繼續利用線性方程最小二乘法擬合并分別求取偏差平方和的方法，比較其離散程度，選取較小的值對應的方案作為最佳處理方法。結果表明，使用該方法能夠通過剔除較少的誤差數據使受特定變化趨勢限制的傳感器數據符合變化趨勢，并且曲線整體變化平穩，可信度較高。本文方法能有效地解決現有技術中存在的因傳感器測量得到的部分數據不符合已知變化趨勢的問題。