梯度密度黏彈性材料的波傳播研究*

李 毅，苗春賀，徐松林,2，張金詠，王鵬飛

（1. 中國科學技術大學中國科學院材料力學行為和設計重點實驗室，安徽 合肥 230027；2. 中國地震局地震預測研究所高壓物理與地震科技聯合實驗室，北京 100036；3. 武漢理工大學材料復合新技術國家重點實驗室，湖北 武漢 430070）

超結構/材料是解決復雜防護效應問題的關鍵之一，是一種微觀異構、宏觀連續的介質，表現出一些特別優異的功能和物理力學性質，例如同時兼具高強度和高韌性，在高技術領域，已經形成了分類眾多的工藝和產品。梯度密度材料是近幾年制作工藝逐漸成熟的一種超結構/材料，形成了生物功能梯度材料、光學功能梯度材料等，并逐漸在多種領域得到了應用。由于這種介質含有大量的多尺度的細微觀結構，這些細微觀結構會使得應力波產生波形彌散和衰減現象[1-2]，其宏觀響應均具有一定的黏彈性特征。研究沖擊載荷作用下這種梯度材料的黏彈性響應特征，有助于揭示介質的細微觀結構對應力波傳播的影響規律，為材料的優化設計提供依據。本文中將結合分離式霍普金森壓桿(SHPB)實驗技術對梯度密度黏彈性材料的沖擊響應進行研究。

SHPB 技術廣泛應用于測量材料動態力學特性[3]。Zhao 等[4]給出了采用黏彈性波導桿時確定試件動態本構關系的方法，Bacon[5]、王寶珍等[6]采用傳播系數法較系統地分析了黏彈性試件中波傳播過程中的彌散和衰減規律，以及動態本構關系的測試方法；朱玨等[7]分析了試件中傳播的黏彈性波對SHPB 實驗過程中應力均勻性等因素的影響規律。黏彈性波的傳播理論是研究波傳播特性的關鍵[8]，Ting 等[9]、Tedsco 等[10]、Han 等[11]基于波動方程的Laplace 變換方法研究了黏性層狀介質中彈性波的傳播特性和頻率域中的等效分析方法，Mukerji[12]通過測試研究了層狀介質中彈性波的衰減和彌散。這些研究對彈性波在不同的多層彈性介質中的傳播規律進行了實驗和理論探索，揭示了彈性波波速對材料細觀結構特征的頻率相關性。進一步，周風華等[13]、鄭宇軒等[14]基于波動方程的Laplace 變換和數值Laplace 逆變換對SHPB 實驗過程中黏彈性波的傳播做了卓有成效的工作。這些研究都是針對均勻的黏彈性材料進行的，如果黏彈性材料不是均勻的，即其密度具有一定的分布特征，則會給波動分析帶來較大的困難。張鳴等[15]基于Euler 方程的形式給出了垂直入射情況下梯度密度黏彈性材料中波動傳播分析的一個近似解，得到了一些初步結論。

基于此，本文中將在張鳴等[15]工作的基礎上，進行垂直入射情況下多層梯度密度黏彈性材料中波動傳播的分析，結合梯度鈦-硼化鈦材料[16]和碳纖維增強樹脂材料[17]進行初步實驗研究。

1 沖擊下多層梯度密度黏彈性介質中波的傳播

1.1 控制方程和近似解

梯度密度黏彈性介質中，密度ρ 是位置x的函數，即：ρ=ρ(x)。其中的變形連續方程、動量守恒方程分別為：

1.2 垂直入射多層梯度介質中波的傳播

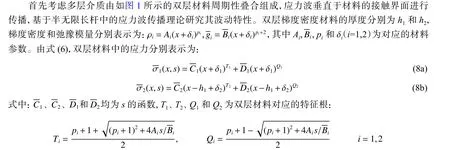
圖 1 垂直入射雙層周期性疊合介質示意圖Fig. 1 Schematic diagram of a two-layer periodically-superimposed medium with normal incidence

2 梯度密度鈦-硼化鈦材料的動力學行為

2.1 材料

梯度鈦-硼化鈦(TiB2-TiB-Ti)陶瓷材料由武漢理工大學材料復合新技術國家重點實驗室采用沉積燒結的工藝制備[16]。梯度材料的第1 層為純鈦，后續各層中逐次減少10%的鈦，并以同體積的硼化鈦進行填充，由此制備的樣品從光亮的白色（鈦）逐漸轉變為暗淡的灰黑色（硼化鈦），如圖2 所示。隨著硼化鈦含量的增加，樣品的硬度[16]逐漸增加，表現出較強的梯度分布特征。對3 個樣品中的密度分布進行統計，沿厚度方向均勻地切取6 個直徑(4±0.1) mm、厚度(1.5±0.1) mm 的圓柱體測量其密度，結果如圖2 所示，隨著硼化鈦含量的增加，樣品的密度逐漸增加。采用 ρ =A(x+δ)p對梯度密度分布進行擬合，δ 取為1.0，可得到密度遞增時的參數為：A=4.45 g/cm3，p=2.0。將此樣品反過來，可得到密度遞減時的參數為：A=4.56 g/cm3，p=-2.45。采用相似的形式也可對梯度硬度的分布進行擬合。

應用SHPB 加載裝置分別對單個試件和兩個樣品組合試件進行動態加載實驗，以對應研究單層梯度介質與雙層梯度介質中應力波的傳播。實驗采用了比較低的沖擊速度，例如本實驗中的5.0 m/s，以研究介質的黏彈性行為。單個試件尺寸為：直徑(13±0.1) mm，厚度(10±0.1) mm。

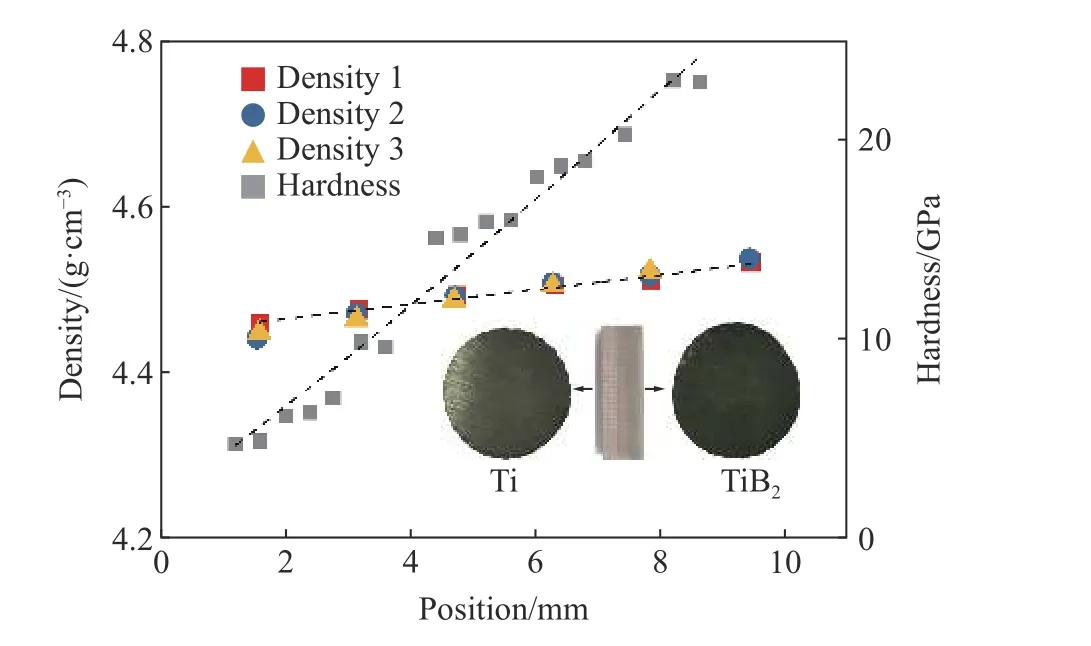
圖 2 梯度鈦-硼化鈦樣品中密度和硬度[16]分布Fig. 2 Distributions of density and hardness[16]in gradient Ti-TiB2 specimen

2.2 單層和雙層梯度鈦-硼化鈦材料的波傳播

實驗中入射波信號如圖3(a)所示，所有實驗中基本控制不變。測得的透射信號如圖3(b)所示，包含有：單層密度遞增、單層密度遞減、雙層密度遞增疊合、雙層密度遞減疊合、單層密度遞增與單層密度遞減疊合，以及單層密度遞減與單層密度遞增疊合等6 組實驗，每組重復3～5 次。

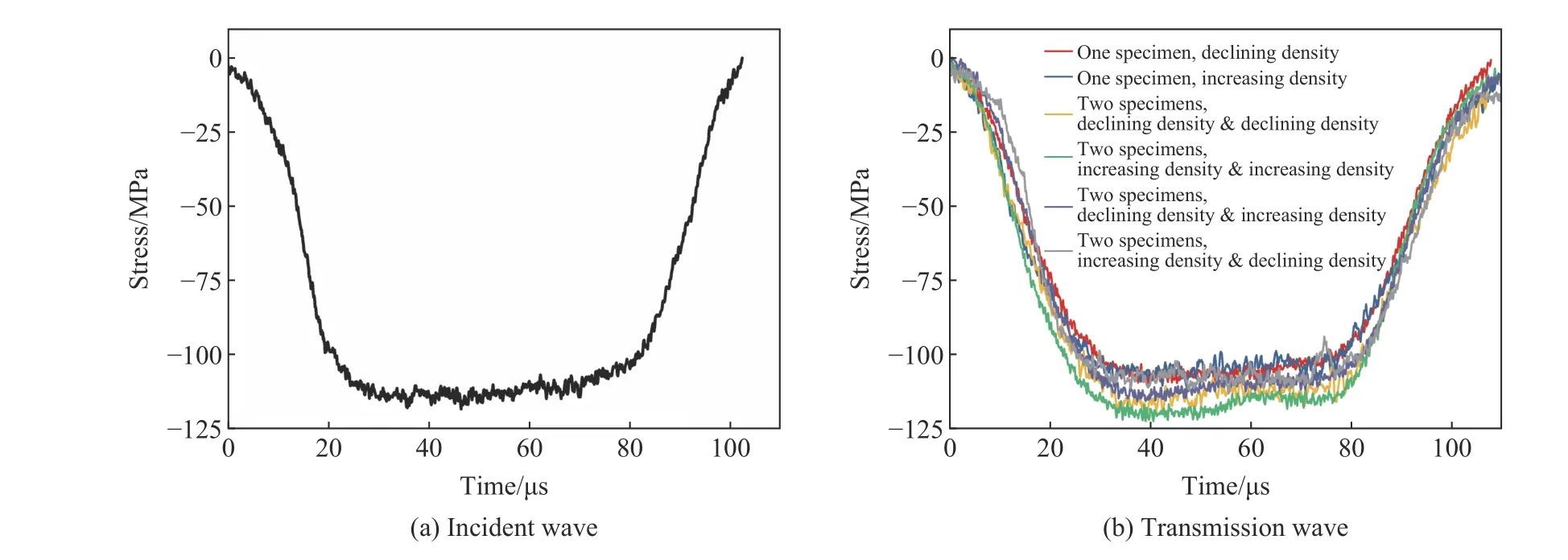
圖 3 梯度鈦-硼化鈦實驗波形Fig. 3 Recorded wave profiles in the gradient Ti-TiB2 specimens

基于上述理論分析，對于單層試件，由解的形式(6)和試件兩端的入射波信號 σin(t) 、透射波信號σout(t) ，可以得到：

將不同試件的入射波信號和透射波信號代入式(16)或式(17)進行計算。由于入射波信號 σint(t) 與透射波信號 σout(t) 均為離散的數據，進行Laplace 數值逆變換計算比較麻煩，因此，為簡化分析過程，對波形的加載部分均采用Asin(wt) 的形式進行擬合，然后進行Laplace 逆變換。圖4 為單層試件的分析結果，其中實線為采用SHPB 實驗的三波法進行處理的結果，虛線為上述理論模型計算的結果，分別進行了試件的撞擊端(x=0)、支撐端(x=L)，以及試件中部(x=L/2)的應力波形的計算。由此可見：(1)三個位置計算得到的應力-時間曲線有一定的差異，說明此梯度鈦-硼化鈦陶瓷材料中內界面的存在，使得梯度材料表現出一定的黏性，雖然還很弱；(2)計算得到的應力-時間曲線與SHPB 三波法處理得到的結果非常接近，此時反射波的波形結構比較簡單，黏性對SHPB 三波法分析影響不大。

圖5 為雙層材料疊合試件的計算結果。實線為采用SHPB 實驗的三波法進行處理的結果，虛線為計算結果，包含了試件的撞擊端(x=0)、支撐端(x=2L)，以及兩個試件之間(x=L)的計算波形，以作對比。由此可見：三波法處理得到的結果與兩個試件中部的計算結果比較接近；3 個位置計算得到的應力-時間曲線的幅值有一定的差別，且密度遞減介質中隨傳播距離的增加，應力幅值減小的幅度相對較大。雖然單層梯度鈦-硼化鈦陶瓷材料中由于內界面的存在產生的黏性不是很強，但是雙層密度梯度材料的疊合制造了新的宏觀界面，使疊合介質整體表現出更強的黏彈性特征，這主要表現在應力幅值和應力波形的上升過程隨傳播距離的增加都出現了明顯變化，反映出一種介質中多種微結構組成導致的黏彈性機制[12]。疊合試件的黏性使SHPB 三波法分析結果與材料的性能之間存在一定的差異。

3 碳纖維增強樹脂材料的動力學行為

3.1 復合材料

碳纖維增強環氧樹脂材料[17]中碳纖維粉末的型號為XGCP-300，密度為1.75 g/cm3。在環氧樹脂中加入4 種質量分數(0%、10%、30%、50%)的碳纖維粉末來制備4 種密度的復合材料，制得的材料如圖6 所示，隨著碳纖維含量的增加，樣品的密度顯著增加，即從質量分數0%時密度為(1.17±0.1) g/cm3，增加到質量分數10%時密度為(1.21±0.1) g/cm3、質量分數30%時密度為(1.35±0.2) g/cm3，最后增加到質量分數50%時密度為(1.57±0.2) g/cm3。環氧樹脂（碳纖維含量0%）弛豫模量為(1.20±0.1) GPa，其布洛克菲爾德黏度為800 MPa·s。隨碳纖維含量增加，弛豫模量增加到質量分數為10%時的(1.24±0.1) GPa、質量分數為30%時的(1.38±0.2) GPa，最后增加到質量分數為50%時的(1.61±0.2) GPa。同時，隨著碳纖維粉末含量的增加，樣品由透明狀逐漸變為黑色；樣品的灰度統計基于試樣表面顯微鏡拍攝圖片分析處理而來，灰度分布隨碳纖維含量的增加向灰度值較小的黑色區域移動，灰度分布區域隨含量的增加越來越集中，樣品的均勻性相對也較好。碳纖維增強環氧樹脂試件表現出明顯的黏性特性；但隨著碳纖維含量的增加，試件顯得越來越脆[17]。

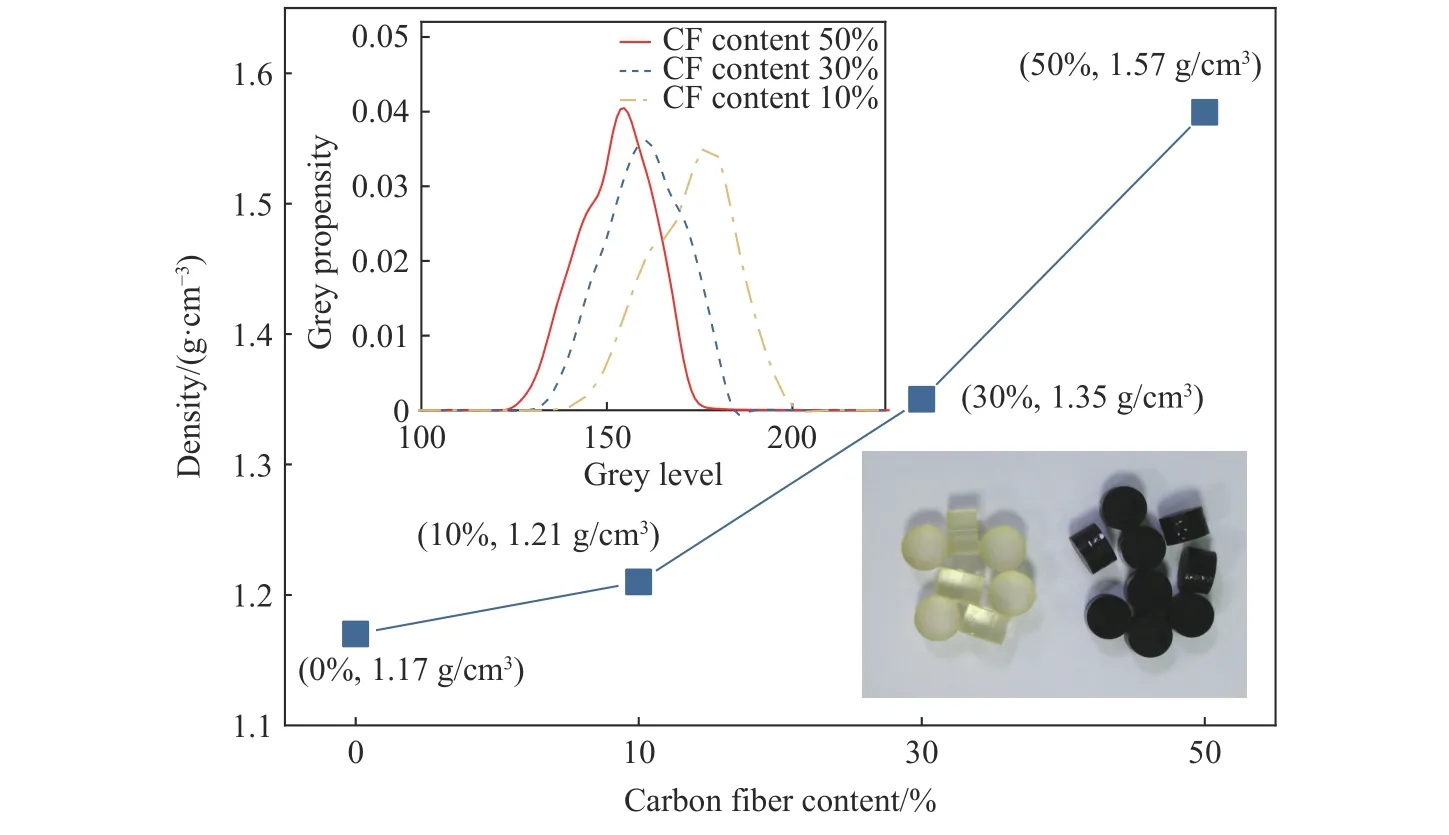
圖 6 制備的碳纖維增強樹脂復合材料的密度隨碳纖維質量分數的變化Fig. 6 Density change of prepared carbon-fiber reinforced resin composites with carbon fiber mass fraction

梯度密度黏彈性材料的制備很困難，初始擬采用不同密度的多層黏彈性材料來疊合成梯度密度介質，但是沖擊實驗成功率非常低，重復性也不好。因此，將僅對雙層黏彈性材料疊合介質應用SHPB 加載裝置進行動態加載實驗，以研究雙層黏彈性介質組成的近似“梯度密度”試件中應力波的傳播。實驗采用比較低的沖擊速度，例如5.0 m/s。單個試件尺寸為：直徑(8±0.1) mm，厚度(4±0.1) mm。

3.2 雙層碳纖維增強樹脂材料中的波傳播

圖7 為雙層材料疊合的近似“梯度密度”試件的計算結果。實線為SHPB 實驗三波法處理的結果，以作對比；分別進行了試件的撞擊端(x=0)、支撐端(x=2L)，以及兩個試件之間(x=L)的應力波形的計算。圖7(a)、(b)、(c)所示雙層疊合材料分別對應碳纖維質量分數由50%減小到30%、10%、0%；圖7(d)、(e)、(f)所示雙層疊合材料分別對應碳纖維質量分數由0%增加到10%、30%、50%。由此可見：三波法處理得到的結果與兩個試件中部的計算結果比較接近；三個位置計算得到的應力-時間曲線的幅值有較大的差別，且隨傳播距離的增加，應力幅值出現較大的減小幅度，表現出比單層材料更強的黏彈性特征。這種黏性特性包含材料本身的黏性和微結構組成導致的黏性等兩種機制。疊合試件的黏性使SHPB 三波法分析結果與材料的性能之間存在較大的差異：由于SHPB 三波法選取了入射桿與透射桿得到的入射波、反射波與透射波，在進行計算時，得到的是兩桿之間試件應力情況的平均值。而實驗所選取的材料具有變密度特性，而且對于碳纖維增強樹脂材料，其兩桿之間的密度變化較大，在試件的不同位置處，其應力會有一定的差距。因此采用SHPB 三波法分析得到的平均應力不能較好地反映試件密度的變化特性，也較難得到試件不同位置的應力變化情況。

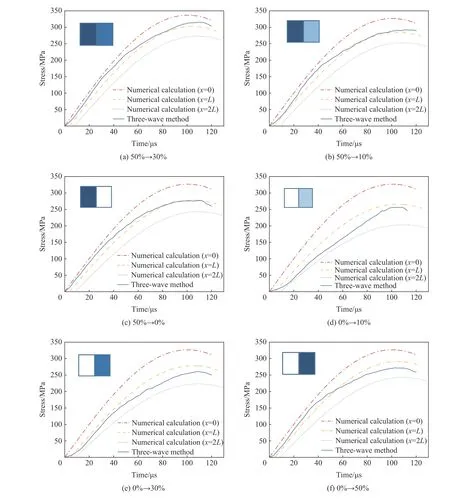
圖 7 雙層碳纖維增強樹脂疊合試件中的應力波形Fig. 7 Stress-time curves in two-layer superimposed specimens of carbon fiber reinforced resin

將雙層材料疊合的試件等效成單層等效的梯度密度黏彈性介質。首先，采用 ρ =A(x+δ)p的形式對近似梯度密度試件進行擬合，δ 取為1.0，可以得到密度遞減時的參數分別為：50% → 30% 時，A=1.57 g/cm3，p=-18.95；50% → 10%時，A=1.57 g/cm3，p=-32.69；50% → 0%時，A=1.57 g/cm3，p=-36.91。以及密度遞增時的參數分別為：0% → 10%時，A=1.17 g/cm3，p=4.22；0% → 30%時，A=1.17 g/cm3，p=17.96；0% → 50%時，A=1.17 g/cm3，p=36.91。其次，采用式(13)求解雙層材料的等效弛豫模量g。由此，計算等效的梯度密度黏彈性介質中波的傳播，結果如圖8 所示，圖中只列出了兩種密度差別較大的情況，即50% → 0%(遞減)和0% → 50%(遞增)。可以看出：兩種計算方法在試件兩側得到的結果基本一致；在試件夾層中間的位置，兩種計算方法得到的結果差別不是很大，但有一些差異，隨密度梯度增大，這種差異也越大。這體現了疊合試件中各種微結構對應力波形產生了影響。

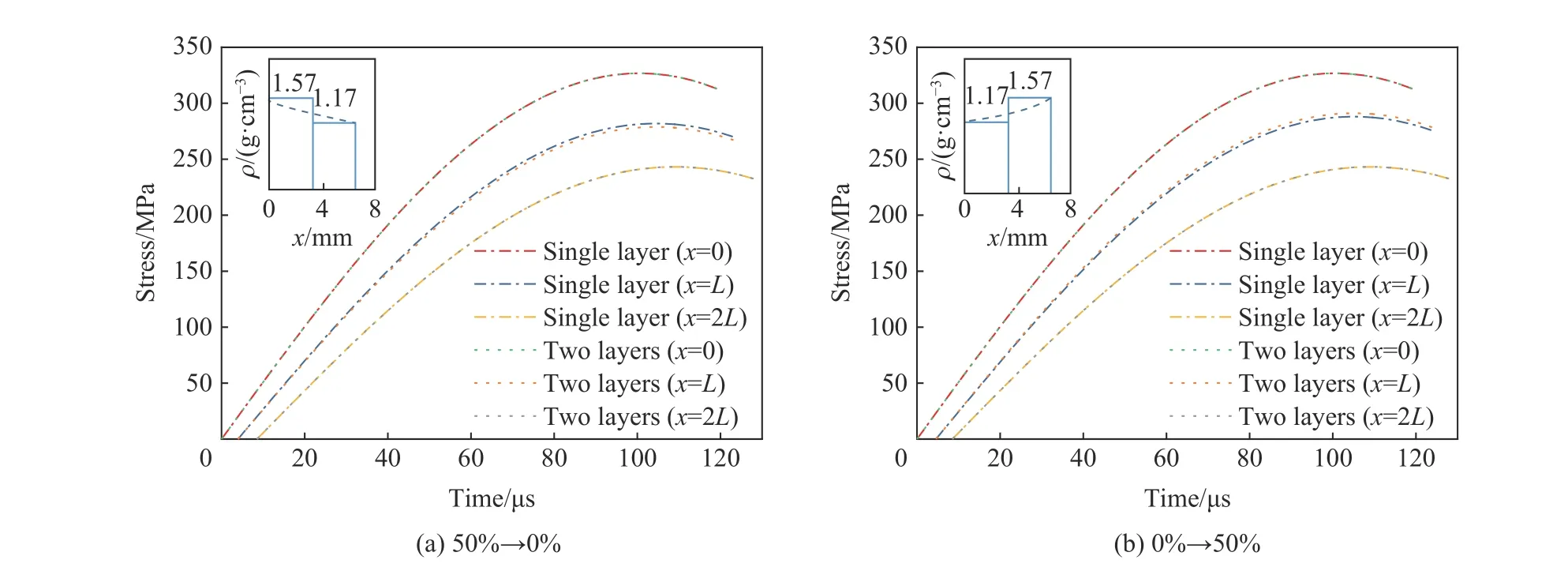
圖 8 等效梯度密度材料和雙層疊合試件中的應力波形的對比Fig. 8 Comparison of stress-time curves in the equivalent gradient-density materials with those in two-layer superimposed specimens

4 結 論

推導了多層梯度密度黏彈性材料中波傳播分析的理論解，結合SHPB 動態實驗技術，分析了梯度鈦-硼化鈦材料與碳纖維增強樹脂材料中波的傳播過程，主要結論如下。

（1）當密度和材料的彈性常數滿足一定的形式時，可得到梯度密度黏彈性材料中波傳播特性的一個近似解。原則上，擬合相關材料系數，此解能夠得到廣泛應用。將此解應用于M層梯度密度黏彈性材料，結合層間的應力與位移連續條件和兩側的邊界條件，可以得到多層介質中波傳播的理論解。

（2）將此理論解應用于單層和雙層梯度鈦-硼化鈦材料，發現：單層梯度鈦-硼化鈦材料中存在內界面，使得其表現出較弱的黏性，但這種黏性對SHPB 三波法分析影響不大；而雙層材料的疊合產生了新的宏觀界面，使其整體表現出更強的黏彈性特征，疊合試件的黏性使SHPB 三波法分析結果與材料的性能之間存在一定的差異。

（3）將此理論解應用于雙層碳纖維增強樹脂材料，發現：隨傳播距離的增加，碳纖維增強樹脂材料中的應力幅值減小較大，表現出更強的黏彈性特征，此過程包括材料本身的黏性和微結構組成導致的黏性等兩種機制。疊合試件的黏性使SHPB 三波法分析結果與材料的性能之間存在較大的差異。

基于此分析方法，為分析材料內部界面的實際情況，可進一步建立界面斜入射的情況。由于試樣制備比較困難，本文的相關結論尚需更多驗證和提高。