基于自適應陷波的光伏逆變器諧振抑制方法

李圣清，沈志超，彭自然，何元銘，谷昕鵬

(1. 湖南工業大學電氣與信息工程學院，湖南株洲412007；2. 光伏微電網智能控制技術湖南省工程研究中心，湖南株洲412007)

0 引言

近年來, 分布式可再生能源發電量在全國總發電量中的比重逐年增加[1-2], 而并網逆變器作為光伏陣列與大電網之間的接口裝置, 顯得尤其重要。為了對并網逆變器裝置進行優化, 提高系統穩定性, 越來越多組串式光伏逆變器被應用于光伏并網系統[3-4], 傳統集中式光伏逆變器無法達到每個光伏陣列最大功率點跟蹤 (maximum power point tracking, MPPT) 效率, 在多臺逆變器并聯的集群系統中采用組串式并網逆變器, 不僅能夠實現所有光伏陣列MPPT 控制, 而且多個光伏陣列與逆變器構成的發電單元并聯接入電網能夠提升系統的容錯率[5-6]。然而, 西部地區的光照更加充足, 經過長距離傳輸線路將系統與公共電網相連使線路阻抗無法被忽視, 導致公共電網顯弱電網特性[7]。在這類情況下, 并網逆變器與電網阻抗發生諧振, 原有控制方法失效, 并網失敗。

上述諧振問題嚴重阻礙了規模化光伏發電技術的發展, 因此, 國內外學者提出了大量抑制諧振的方法。文獻 [8] 提出在公共耦合點處增加自適應有源阻尼器以確保并網系統穩定, 并采用陷波器及比例多諧振補償器消除低次諧波。文獻 [9] 提出采用雙二階濾波器并在線修正陷波器頻率, 但是以上方法均未驗證多臺逆變器并聯時的情況。文獻[10] 在不改變逆變器拓撲結構的前提下, 提出了分支電壓與電流雙反饋協同控制的方法, 但是僅建立了單相逆變器并聯模型, 未驗證三相逆變器是否適用。文獻 [11] 從頻域角度研究了單臺并聯逆變器的阻抗模型, 并進一步分析多逆變器并聯的陷波控制方法, 但是沒有考慮電網阻抗對系統穩定性的影響。

針對這些問題, 文中首先對弱電網情況下的LCL 型組串式光伏逆變器系統結構及LCL 濾波器特性進行分析, 然后在傳統陷波器控制的定電網阻抗系統諧振抑制效果差的基礎上, 提出采用準被動測量方式實時測量電網阻抗, 更新改進后的陷波器及QPR 控制器參數, 得到系統的控制結構框圖并對比分析其穩定性, 最后通過Matlab 搭建兩臺組串式光伏逆變器集群系統證明所提諧振控制方法能有效抑制諧振。

1 組串式光伏集群并網系統

1.1 系統結構

組串式光伏逆變集群系統結構如圖1 所示。

圖1 中, 光伏并網系統包括光伏電池板、升壓電路、逆變器、LCL 濾波器和弱電網這5 個部分。PVi為組串式光伏陣列, 其中,i＝1, 2, 3…,n。MPPT 為光伏陣列的最大功率點跟蹤模塊。由直流側電感Ldci、穩壓電容Cdci和二極管、三極管構成的DC/DC 變換器與DC/AC 變換器組成了兩級式變換器, 通過LCL 濾波器與弱電網相連。uPCC為公共耦合點電壓。弱電網包括阻抗Rg、Lg和電網電壓ug。iL1n、iL2n、ig分別為逆變器側電感電流、網側電感電流、并網電流。

圖1 組串式光伏逆變器集群系統結構

1.2 LCL 濾波器特性分析

LCL 濾波器由逆變器側電感L1i、弱電網側電感L2i和濾波電容C1i構成,RL1i與RL2i為濾波電感的寄生電阻。由文獻 [12] 可知, 弱電網中的阻性分量能夠增加系統的阻尼, 提高系統穩定性。為驗證所提控制方法在系統諧振最嚴重情況下的抑制能力, 假設文中弱電網為純感性, 即阻抗只含有Lg。單臺逆變器的LCL 濾波電路如圖2 所示。

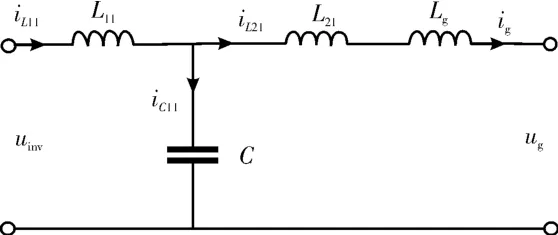
圖2 LCL 濾波電路

若忽略寄生電感, 由圖2 得uinv至并網電流ig的開環傳遞函數為:

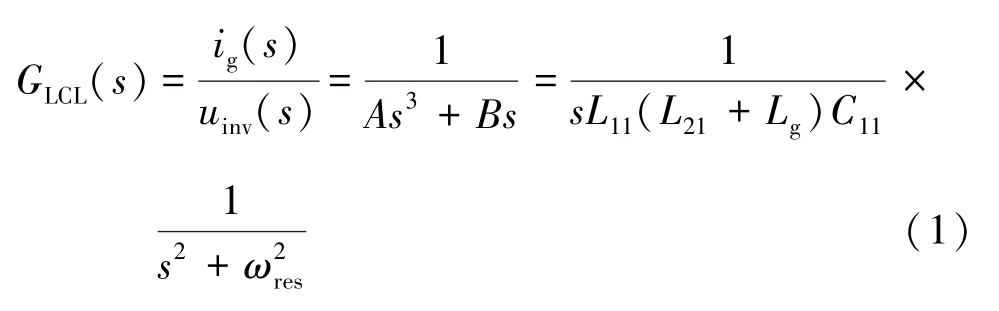
式中,A＝L11(L21+Lg)C11,B＝ (L11+L21+Lg),ωres為LCL 濾波器的諧振角頻率, 則諧振頻率表達式為:

由文獻 [13] 可知, 當并網逆變器臺數增加到n時, 諧振頻率為:

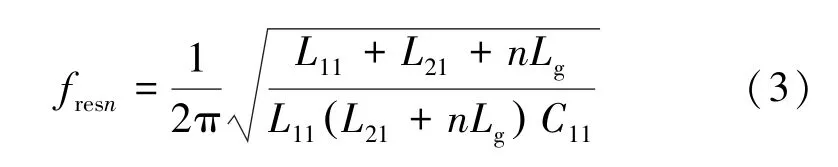
通過式 (3) 可得諧振頻率與并聯臺數及電網阻抗間關系如圖3 所示, 隨著逆變器并聯臺數n增加或電網阻抗Lg增大, 諧振頻率fres減小, 在n≥200 時,fres值穩定。

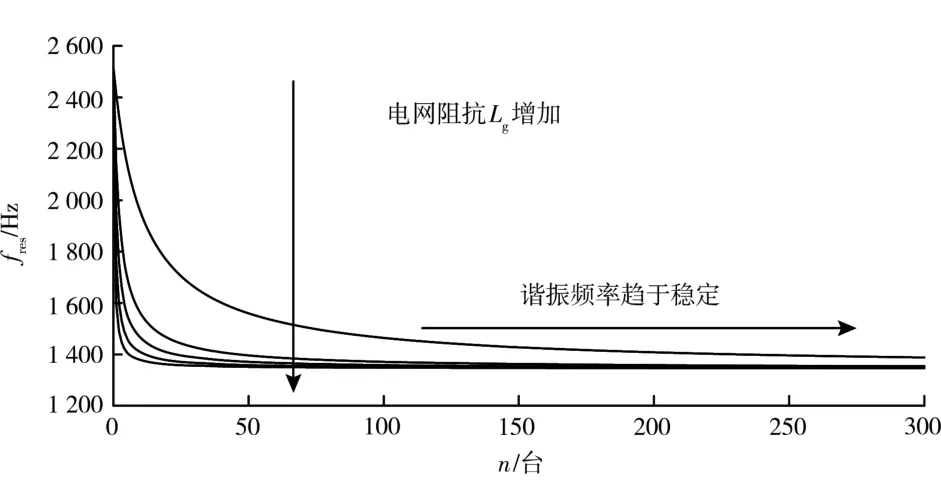
圖3 諧振頻率與并聯臺數及電網阻抗間關系

對諧振頻率fres、電網阻抗Lg與控制器參數優化可知, 電網阻抗實時測量環節必不可少。

2 傳統組串式光伏逆變器諧振抑制方法

相較于L 型濾波器, LCL 型濾波器階數較高,存在諧振尖峰, 因而需要增加系統阻尼來抑制諧振。

目前, 使用最廣泛的兩種抑制諧振尖峰的方法為: 一是無源阻尼法, 加入實際電阻；二是有源阻尼法, 既可通過改變系統控制結構增加系統阻尼,如電容電流反饋有源阻尼法, 也可通過在系統前向通道中加入濾波環節, 例如, 在圖4 傳統控制結構框圖中加入虛線框內所示濾波環節。

圖4 傳統控制方法框圖

文中采用陷波濾波器, 并引入并網電流反饋。其中,Ga(s) 為 PI 電流控制器,Ga(s)＝kp+ ki/s,逆變器等效增益KPWM＝1。陷波濾波器傳遞函數如式 (4) 中GN(s) 所示, 其中Q為陷波品質,ωa為陷波角頻率。

結合式 (4) 及圖4 可得傳統控制方法的系統開環傳遞函數為:

GN(s)中ωa＝2πfa, 經化簡可得雙二階陷波器傳遞函數為:

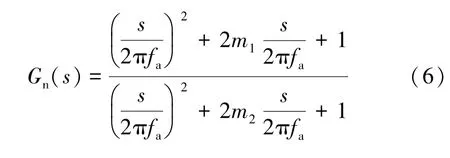
由圖5 可知, 加入陷波器可抑制由LCL 濾波器帶來的特定諧振頻率fres處的諧振尖峰, 而不影響其他頻率。

圖5 LCL、Notch 伯德圖

結合式 (5)、(6) 可得系統開環傳遞函數為:

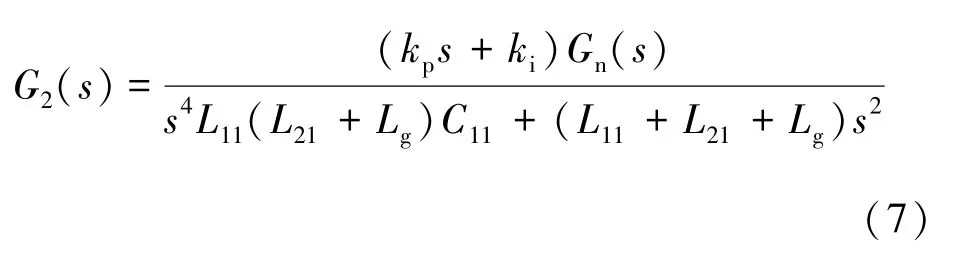
電網阻抗對系統穩定性影響如圖6 所示, 由于弱電網下電網阻抗Lg的不確定性, 在Lg逐漸增大的情下, 諧振頻率fres不斷減小, 系統幅值減小,穩定性降低, 相角在fres處發生-180°跳變從而引發系統諧振。

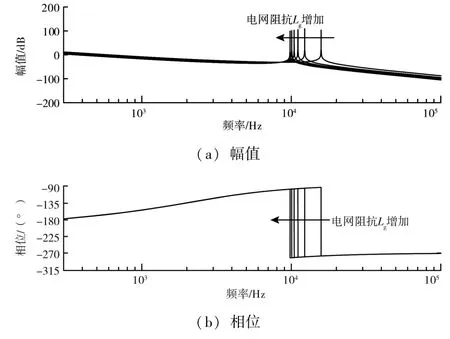
圖6 電網阻抗對系統穩定性影響

3 自適應陷波的組串式光伏逆變器諧振抑制方法

3.1 系統控制結構

為了解決傳統控制方法帶來的系統穩定性差的問題。首先將PI 控制器替換為QPR 控制器能夠更好地無靜差追蹤特定頻率, 如文中所需的fres。

式中,kp為比例系數；kr為諧振系數；ω0為基波角頻率；ωi為截止角頻率。裝機容量 3GW 以下電網頻率通常為50 Hz±0.5 Hz, 式 (8) QPR 傳遞函數中的2ωi雖然使fres處的增益減小, 但是引入了一個較大的帶寬, 以此來減小電網頻率波動帶來的影響。

然后, 對式 (6) 中涉及到的比例系數m1、m2進行選取。由圖 7、8 可知, 圖 7 中比例系數m1、m2由 2×10-4、2×10-1減小或增大到 0.2×10-4、0.2×10-1、5×10-4、5×10-1時,m1/m2不變, 則陷波深度不變, 帶寬隨m1、m2減小而減小；圖 8 中比例系數m1、m2由 5×10-4、5×10-1減小或增大到5×10-6、5×10-1, 5×10-2、5×10-1時,m1/m2改變,則帶寬不變, 陷波深度隨m1/m2減小而增大。

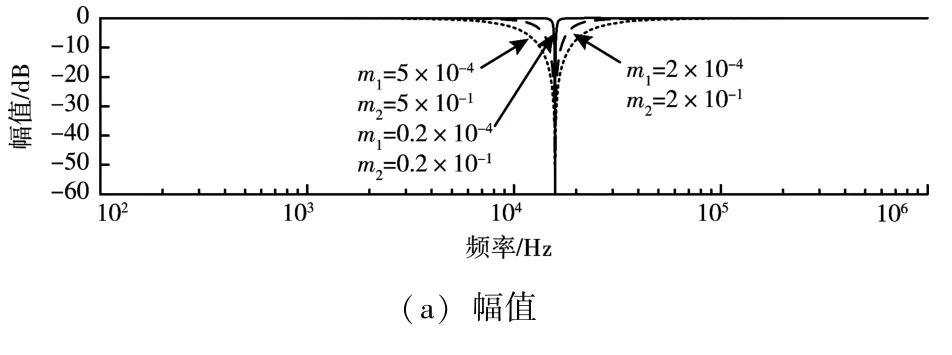
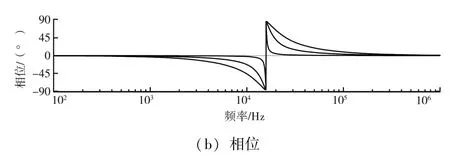
圖7 m1/m2 不變時的陷波器伯德圖

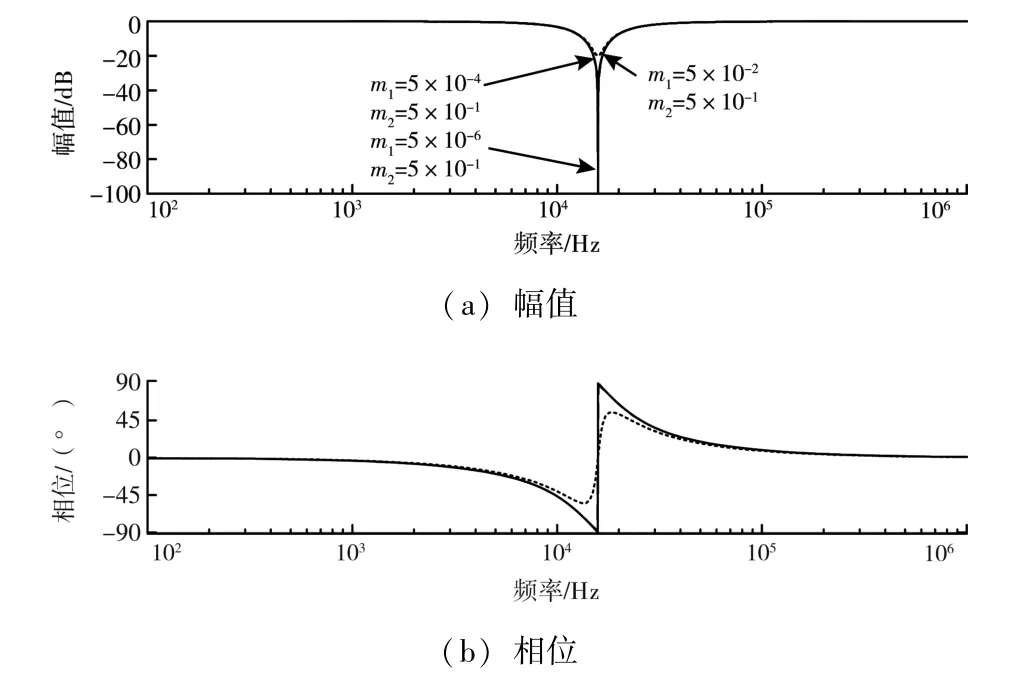
圖8 m1/m2變化時的陷波器伯德圖

最后, 得出改進后控制方法框圖如圖9 所示。

圖9 改進后控制方法框圖

由圖9 可得改進后系統開環傳遞函數為:

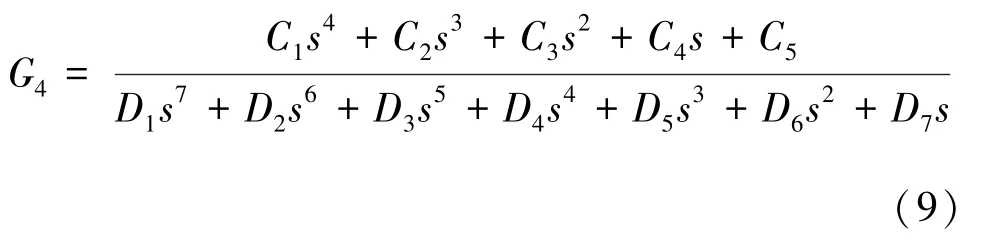
式中,

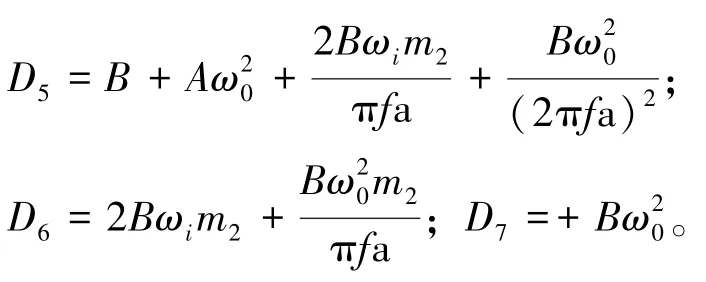
3.2 參數自適應系統

電網阻抗值實時變化的特性導致系統需要相應的高精度測量方法以解決其與系統諧振頻率的關聯性。

3.2.1 電網阻抗自適應

電網阻抗準被動測量方式如圖10 所示, 采用小信號注入法, 在檢測到電網阻抗變化Rest大于或等于閾值時啟動主動測量。分別采集兩臺并網逆變器電網側電感電流送入Lg準被動測量模塊, 得到更新后的Lg等效至L2中。

圖10 電網阻抗準被動測量方式

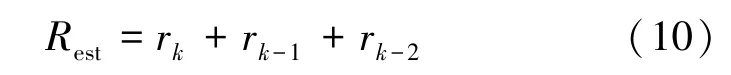
式中,ik＝kTs,ik-1＝ (k-1)Ts；ik-2＝ (k-2)Ts；Ts為系統采樣時間。

3.2.2 電流控制器自適應

采用QPR 控制器, 引用文獻 [14] 中的參數設計原則, 可計算出QPR 控制器中所涉及的參數kp、ωi、kr。但是, 由文獻 [15] 可知, 為保證系統良好的相位裕度 (Phase Margin, PM), 需要提高系統開環增益, 保持系統帶寬不變。因此, 設實時測得諧振頻率為fb, 則有諧振頻率fa與fb比值的平方α為:

在低頻段忽略濾波電容帶來的高階項, 可得僅并網電流反饋的系統開環傳遞函數為:

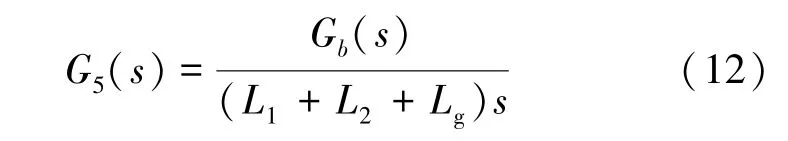
將α代入式 (12) 可得:

則有優化函數F(α) 與自適應QPR 函數為:

綜上所述, 改進后系統伯德圖如圖11 所示,與圖6 比較可知, 諧振點處波形平滑, 系統穩定。

圖11 改進后系統伯德圖

4 仿真驗證

為驗證改進后集群諧振抑制方法的正確性及有效性, 文中使用Matlab/Simulink 搭建了兩臺組串式光伏逆變器系統的仿真模型, 控制原理如圖12所示, 系統所涉及參數見表1。

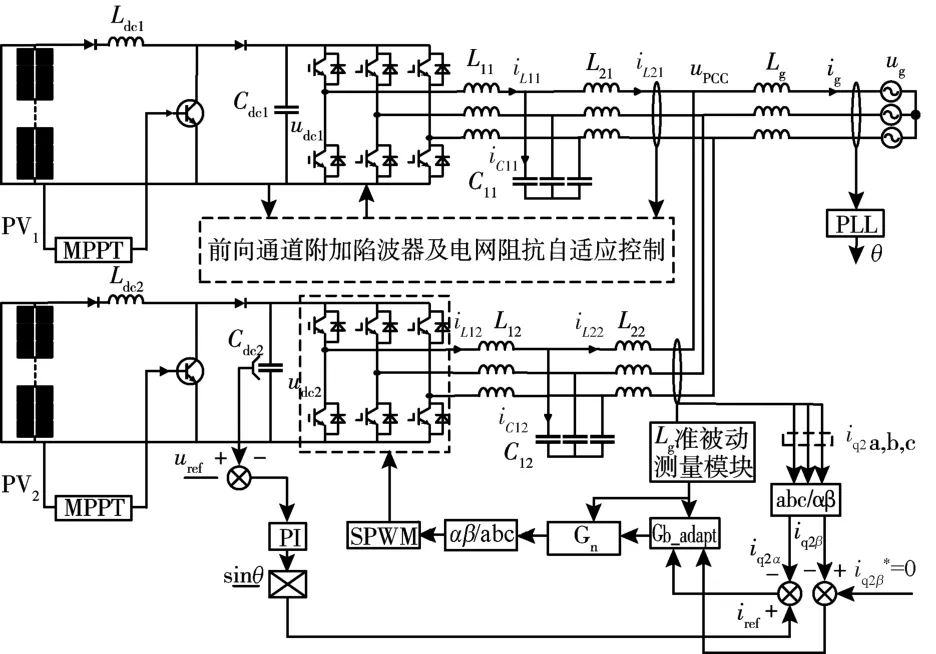
圖12 2 臺組串式光伏逆變器并網系統控制圖

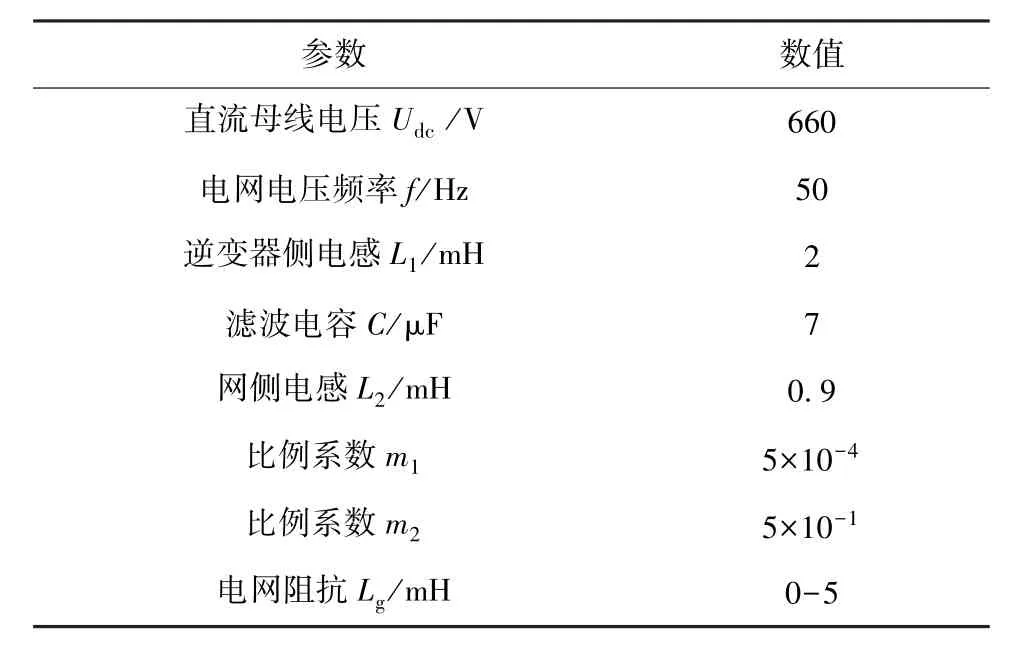
表1 系統參數

以第二臺逆變器為例, 改進前后并網電壓電流波形, 并網電流 FFT 分析分別如圖 13、14、15所示。

圖13 Lg ＝1 mH 時改進前的并網電壓電流波形

圖14 Lg ＝1 mH 時改進后的并網電壓電流波形

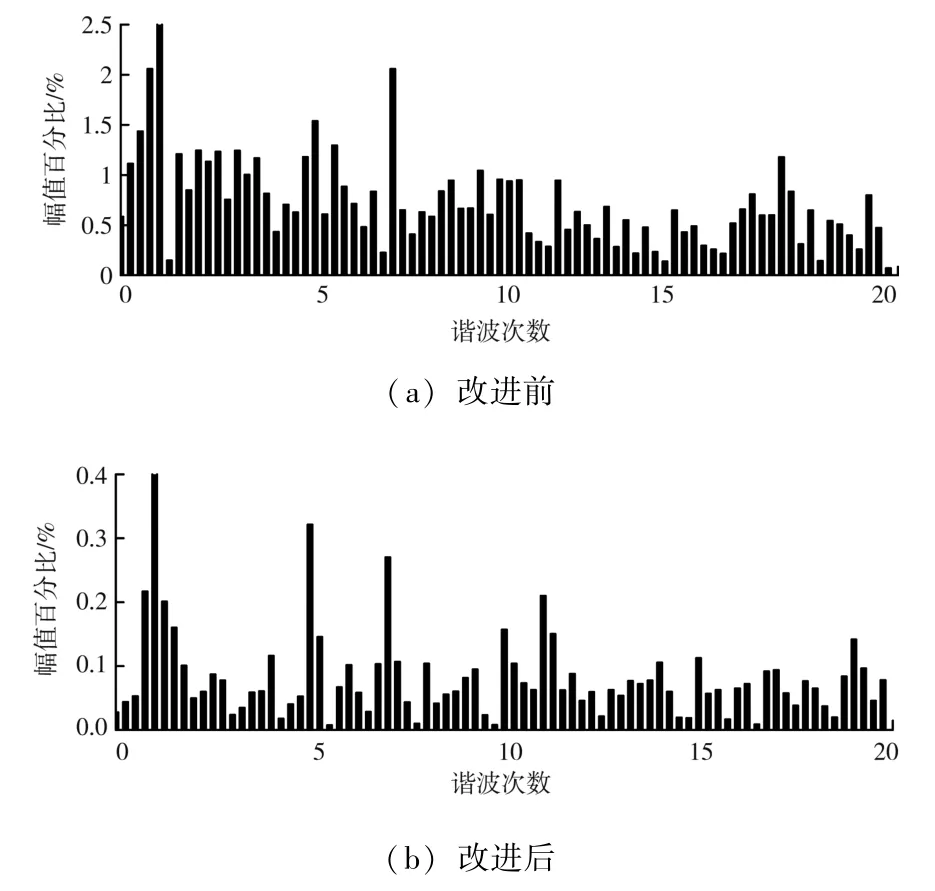
圖15 Lg ＝1 mH 時改進前后的并網電流FFT 分析

由圖15 可知, 改進前并網電流波形畸變嚴重,諧波含量THD 為8.42%, 在加入改進后的陷波器及電網阻抗自適應控制后諧波含量THD 減小到3.10%, 系統諧振得到有效抑制。此外, 由于電網電壓的背景諧波電壓, 改進后的FFT 分析中含少量 3、5、7 次低次諧波。

考慮實際電網環境下電網阻抗值會有波動, 在Matlab 中, 當電網阻抗在0.15 s 時由4 mH 減小為1 mH, 為驗證系統動態性能, 分別對加入自適應陷波前后的系統進行仿真, 仿真波形如圖16、17所示。

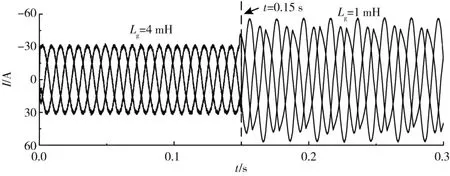
圖16 未加入自適應陷波的并網電流波形

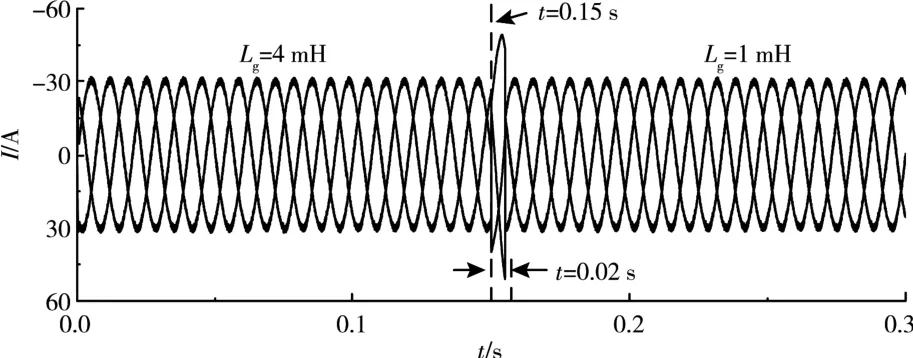
圖17 加入自適應陷波的并網電流波形

由圖16 可知, 未加入自適應陷波的系統并網電流在0.15 s 后發生波動且系統無法保持穩定, 而圖17 中加入自適應陷波的系統, 首先在0.15 s 時檢測到電網阻抗發生改變, 然后在0.02 s 內重新測量和分配電網阻抗值, 并更新系統參數, 最后并網電流經過短暫波動后恢復穩定, 系統也趨于穩態。

5 結論

文中針對弱電網情況下組串式逆變器集群諧振問題, 提出了一種基于改進型陷波器的諧振抑制方法, 該方法通過伯德圖分析電網阻抗對并網系統的影響, 得出以下結論:

1) 并網系統中諧振頻率與并網逆變器臺數和電網阻抗成負相關, 電網阻抗與并網系統穩定性成負相關。

2) 加入電網阻抗準被動測量模塊后, 電流控制器QPR 及陷波器傳遞函數能得到實時更新。

3) 在多臺逆變器并聯接入系統時, 改進后的并網系統能快速分配每臺逆變器網側電感值, 有效抑制系統諧振。