靜位移法求解理論力學中單自由度系統的自由振動問題

楊靜寧，趙永剛*，張亞民，雷芳明

(1.蘭州理工大學理學院，730050，蘭州；2.中如建工集團有限公司，226500，江蘇，南通)

0 引言

振動現象廣泛存在于日常生活或生產實踐中，也是工程實踐中經常遇到的現象。而在工程實際中，經常遇到的最簡單的振動系統則是單自由度系統，單自由度系統的自由振動反映了振動的一些最基本的規律。現行的理論力學教科書中，對振動系統(尤其是單自由度系統)微幅自由振動的固有頻率求解均作了介紹。通常情況下，單自由度系統微幅自由振動的固有頻率可通過振動的微分方程、能量法以及靜位移(靜變形)法3種途徑來求解。但是現有教科書[1-5]以及相關資料[6-8]中大多通過微分方程和能量法來求解單自由度系統自由振動的固有頻率，而對靜位移法介紹甚少。本文將對靜位移法做進一步的討論和推廣，得到了利用系統在外力(外力偶)作用下產生的靜位移(靜角位移)來求一般單自由度系統微幅自由振動固有頻率的一般方法。

1 理論分析

如圖1所示，鉛垂平面內的質量-彈簧系統，彈簧(彈性元件)的剛性系數為k，物體(慣性元件)的質量為m。圖1中δsd為物體產生的微小位移，稱為靜位移。以平衡位置為鉛直坐標x的原點，其自由振動微分方程為[5]

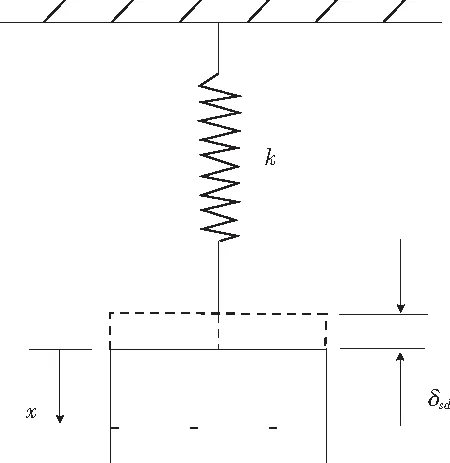
圖1 鉛垂面內的質量-彈簧系統

(1)

固有頻率為

(2)

一般的單自由度振動系統，均可簡化成如圖2所示的質量-彈簧系統。設等效在集中質量點的質量為m，等效剛性系數為k。在集中質量點加一振動方向上的小常力F，m產生的靜位移為δsd，則δsd=F/k，以平衡位置為坐標x的原點，微幅自由振動時的振動方程與式(1)相同，固有頻率為

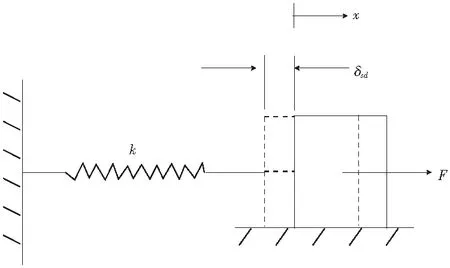
圖2 單自由度系統的簡化模型

(3)

由振動方程可見，此常力并不影響系統自由振動的固有頻率；而從式(3)可知，固有頻率可通過外力F和外力作用下產生的靜位移δsd來計算。

水平面內可繞定軸轉動的剛體，如圖3所示。盤簧的剛性系數為k，剛體繞定軸的轉動慣量為J，在小的外力偶M作用下轉過一個角度φsd=M/k，稱為靜角位移。以相對于平衡位置的轉角φ為位移坐標，其自由振動微分方程為

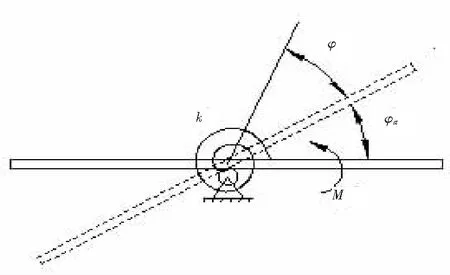
圖3 水平面內可繞定軸轉動的剛體

(4)

(5)

考慮一般的有轉動的單自由度振動系統(如具有一個自由度的平移剛體或機構)，由于是單自由度系統，運動中各構件角速度ωi的比例關系可由各構件間的運動關系確定。設系統微幅振動時，各構件對其各自速度瞬心的轉動慣量為Ji，則定義系統對于第j個構件瞬心的廣義轉動慣量(平移剛體可設與運動方向垂直線上一點為其速度瞬心，按集中質量來計算，對廣義轉動慣量不產生影響)為

在第j個構件上作用一轉動方向上的小力偶M，該構件在振動方向上繞瞬心轉過一個微小轉角φsd，此時振動系統的固有頻率可表示為

(6)

2 實例分析

2.1 無轉動的振動

如圖4所示，斜面上的質量-彈簧系統，集中質量為m，彈簧的剛性系數為k，斜面的傾角為α，在重力作用下物體的靜位移[5]為δsd=mgsinα/k，由式(3)可知其固有頻率為

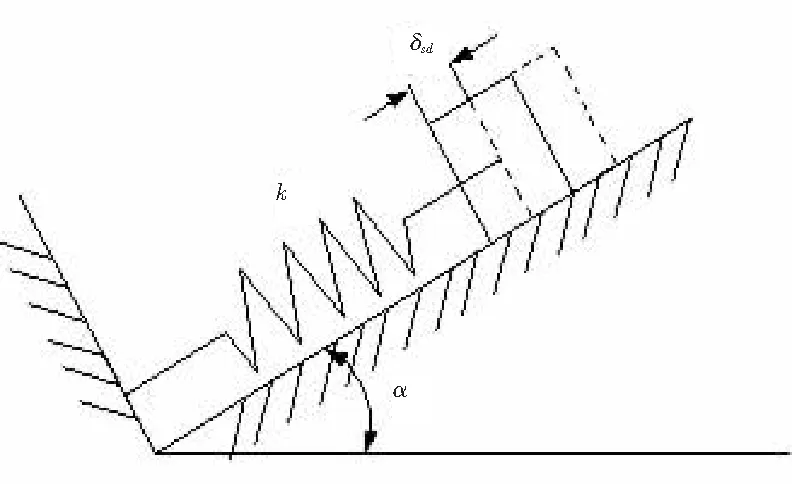
圖4 斜面上的質量-彈簧系統

而由式(2)得出的結果是錯誤的，這是因為重力作用的方向和振動方向不同。

2.2 有轉動的振動

如圖5所示的有轉動的系統，設繩子不可伸長，均質圓輪半徑為r，對輪心的轉動慣量為J，物體重P=mg，彈簧的剛性系數為k。不考慮輪軸的摩擦，則靜位移δsd=P/k，靜角位移φsd=δsd/r=P/(rk)。系統對輪心的廣義轉動慣量為JQ=J+mr2，根據式(6)，系統的固有頻率為

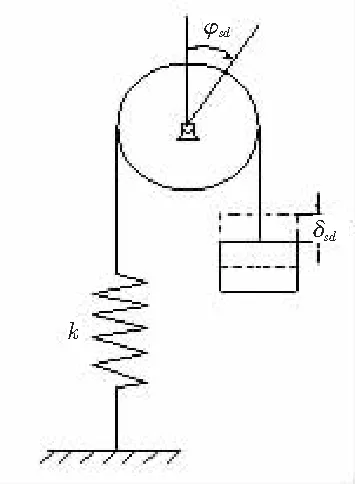
圖5 有轉動的單自由度系統

(7)

而根據式(3)得出的結果是錯誤的，這說明系統中的構件有轉動時，式(3)將不再適用。

2.3 多機構的振動

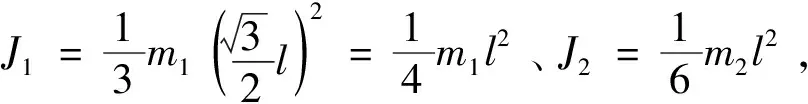
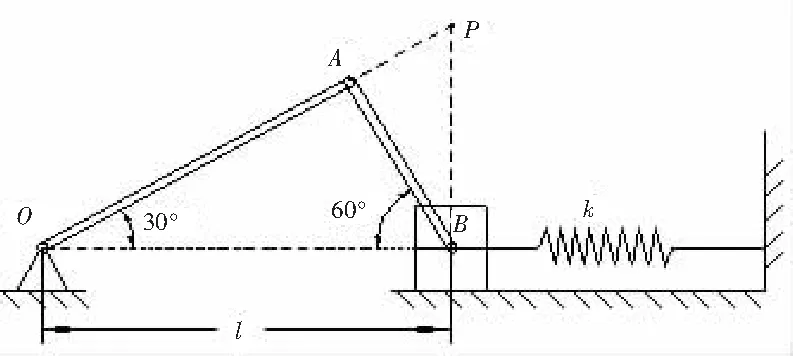
圖6 與彈簧及滑塊相連的曲柄連桿機構

(8)

這說明系統中的構件有轉動時，可利用任一構件的靜角位移來計算固有頻率。

2.4 平面運動剛體的振動

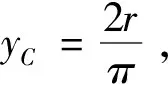
若水平面是光滑的，半圓環此時的速度瞬心在C點，如圖7(b)所示，則固有頻率

(9)

若水平面是粗糙的，半圓環微幅振動時為純滾動，瞬心在A點，如圖7(c)所示，則固有頻率

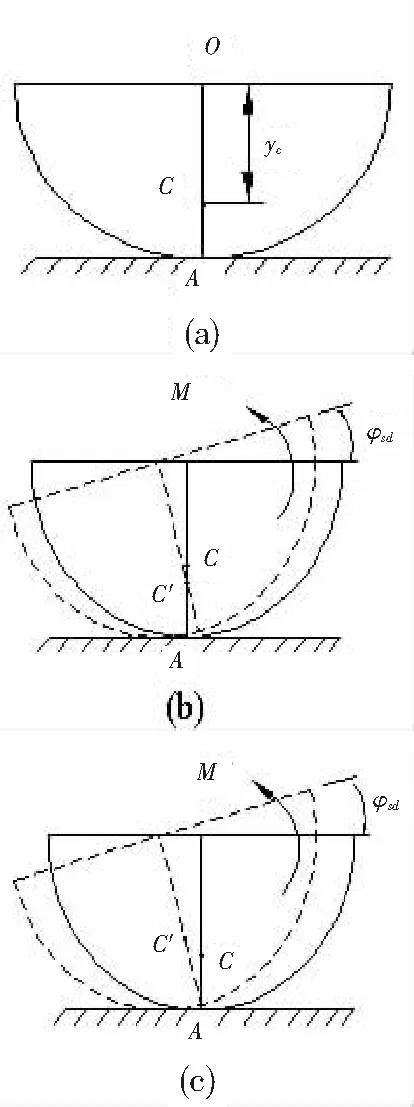
圖7 垂直放置在水平面上做微幅自由振動的半圓環

(10)

可以看出，利用靜位移法求解此振動系統固有頻率簡捷有效。

3 結束語

本文對靜位移法作了進一步的討論和推廣，得到了利用系統在外力(外力偶)作用下產生的靜位移(靜角位移)來求一般單自由度系統微幅自由振動固有頻率的一般方法，此方法簡潔有效，可用于理論力學教學的補充。并得出如下結論。

1)單自由度系統微幅自由振動時的固有頻率可利用在其振動方向上作用常力時產生的靜位移，通過式(3)或式(6)計算求得。

2)所加的微小常力的方向必須是在振動方向上，靜位移為此力作用處的微小位移。

3)系統中的構件沒有轉動時可應用式(3)計算其固有頻率，若存在轉動構件則必須應用式(6)。

4)應用式(6)時，可把機構的振動等效到任一轉動剛體上，不影響固有頻率計算結果的正確性。