基于鄰層傳播的相對重要節點挖掘方法

趙 娜，李 杰，王 劍，彭西陽，景 銘，聶永杰，郁 湧*

(1. 云南大學軟件學院 昆明 650091；2. 云南大學云南省軟件工程重點實驗室 昆明 650091；3. 云南電網有限責任公司電力科學研究院 昆明 650217；4. 昆明理工大學信息工程及自動化學院 昆明 650504)

分析復雜網絡中的節點重要性，是一個被廣泛關注且具有重要意義的研究方向。目前，節點重要性的研究方法主要是針對網絡中的所有節點做全局排序，以判斷節點重要性[1-3]。然而，“相對于一個或一組特定的節點，網絡中哪些節點是最重要的?”這類問題顯示了節點的相對重要性、局部重要性同樣具有較強的現實意義，尤其是當網絡的規模非常大的時候。解決這類問題的一種典型辦法就是先量化一個節點相對于一個已知重要節點的重要性(稱為相對重要性，有時也稱為接近性或者相似性)，再計算一個節點相對已知的重要節點集的重要性，從而找到相對重要節點，即相對重要節點挖掘[4]。如在罪犯關系網絡中，通過已知罪犯查找其余罪犯[5-7]；在蛋白質網絡中，通過已知致病基因查找未知致病基因[8]，或通過已知染病節點查找或預測風險節點[9]；在傳染病網絡中，可針對已知感染人員，優先找出易感人群進行治療、隔離，有效防止病毒的傳播和擴散；在電力網絡中，通過已知重要斷路器或發電單元找出相對重要的斷路器、發電單元等進行保護，可有效防止由相繼故障引起的大范圍停電。可見，挖掘網絡中的相對重要節點具有重要的應用價值。

1 相對重要節點挖掘算法研究現狀

相對重要節點挖掘的工作可以追溯到文獻[10]在2000 年提出的一種個性化的變種HITS 算法研究工作。其后，文獻[11-12]分別提出了個性化變種PageRank 算法，開始更多地考慮網絡中節點的相對重要性。2003 年，文獻[13]定義了相對重要節點挖掘算法的通用框架，還明確提出了網絡中節點的相對重要性是相對于一個或一組指定的特定節點集的重要性。隨后相對重要節點的算法不斷被提出。文獻[14]提出了路徑概率求和的方法，該方法將節點s相對于最近鄰居節點s′的重要性定義為隨機游走過程中從節點s跳到節點s′的概率。文獻[15]提出集群粒子傳播法來評價節點的相對重要性。文獻[16]采用最短距離本身作為相對重要性衡量指標，文獻[17]采用最短路徑距離的P范數的倒數作為相對重要性衡量指標。文獻[18]在介數中心性的基礎上提出了信賴值的方法查找犯罪網絡中的其余罪犯。盡管相對重要性挖掘方法已有一些成果，但仍存在諸多問題，如方法的效率和準確性有待提高；在不同網絡上，方法的參數也需要明確如何選取等。

2 基于鄰層傳播的相對重要節點挖掘方法

在現實生活中，人類遺傳病通常由多種致病基因(含未知和已知的基因)引起，由于它們導致相同或相似的疾病表型，因此未知的致病基因與已知的致病基因功能相關性越強，即某一基因與已知致病基因有越多的關聯，該基因為致病基因的概率越大[19]。基于此思想，本文提出一個新的基于鄰層傳播(neighbor layout diffuse, NLD)的方法來挖掘相對重要節點，該算法的核心思想是：在網絡中，與已知重要節點連接越多的節點，該節點與已知重要節點具有的共同特征越多，其為已知重要節點的相對重要節點的概率越大。

2.1 問題定義

對于由N個節點構成的網絡G(V,E)，其中，N1個 節點構成重要節點集V1，N2個節點構成非重要節點集V2。 重要節點集V1=R∪U，其中R是已知重要節點集，U是未知重要節點集。

本文的工作是：基于已知重要節點集R，分析目標節點集T=V-R中任意節點t相對于已知重要節點集R的重要性，最終找出目標節點集T中top-k個相對重要節點，并對結果進行AUC、準確率和召回率分析。

2.2 NLD 算法中的分層

NLD 算法分為分層和傳播兩個步驟，傳播是在分層的基礎上進行的。分層是將已知重要節點作為第一層，放入集合L1，將第一層節點的鄰居節點作為第二層，放入集合L2，將第二層節點的鄰居節點(不在第一層)作為第三層，放入集合L3，以此類推，直到將所有節點進行分層，得到分層結果Layer={L1,L2,···,Lm}。

2.3 NLD 算法的傳播

在上述分層過程完成后，算法進入傳播步驟。NLD 算法的傳播采用相對重要性分數值來量化節點重要性的傳播情況。分層后，只有第一層節點為已知重要節點，且相鄰兩層的節點間有鏈接。設第一層的相對重要性分數值為1，其他節點的值為0。第一次傳播時，由于第二層節點與第一層節點有鏈接，因此將第一層節點的相對重要性分數值通過鏈接傳給第二層，即將第一層節點的重要性傳給第二層，第二層任意節點與第一層節點聯系越多，被傳給的值就越多，即被傳給的重要性越大。第二次傳播時，把第二層節點作為傳播源，第二層節點通過鏈接會傳給相鄰的第三層，同時會回傳給相鄰的第一層，以此類推。需要說明的是回傳影響的僅是上一層，而下一層的節點值往往小于上一層的，所以回傳的值會更小，回傳不會影響整體的排序結果，并且能對上一層節點的相對重要性進行區分。NLD 算法描述如下：令傳播輪數為S，初始時，S=0，令已知重要節點集R中任意節點r的相對重要性分數值Zr(0)=1，目標節點集T中的任意節點t的相對重要性分數值Zt(0)=0。

第一輪傳播時，S=1，對于第一層中任意節點i，其相對重要性分數Zi(0)≠0 ，將Zi(0)/k傳遞給鄰居，k為節點度數；第二輪傳播時，S=2，對于第二層中任意節點i，其相對重要性分數Zi(1)≠0，將Zi(1)/k傳遞給鄰居，以此類推，當S=m-1 時，網絡中任意節點i的相對重要分數Zi(S)≠0，停止傳播。對于任意節點i，相對重要性分數值Zi(S)的公式表示如下：

傳播結束后，比較所有節點的相對重要性分數值，相對重要性分數值越大的越可能是相對重要節點。

2.4 方法示例

以圖1 所示的網絡為例，說明鄰層傳播算法的計算過程。

圖1 示例網絡

把圖中節點按順序編號為[1, 2, 3, 4, 5, 6, 7, 8,9, 10]。設節點1 為已知重要節點。首先根據已知重要節點對網絡進行分層。節點1 屬于第一層，節點2, 3, 4 屬于第二層，節點5, 6, 7, 8 屬于第三層，節點9, 10 屬于第四層。

初始時，根據節點編號順序，節點對應的相對重要性分數值為[1, 0, 0, 0, 0, 0, 0, 0, 0, 0]。經過第一輪傳播后，各節點對應的相對重要性分數值為[1, 0.333 3, 0.333 3, 0.333 3, 0, 0, 0, 0, 0, 0]。

經過第二輪傳播后，各節點對應的相對重要性分數值為[1.388 9, 0.333 3, 0.333 3, 0.333 3, 0.277 8,0.111 1, 0.111 1, 0.111 1, 0, 0]。

經過第三輪傳播后，各節點對應的相對重要性分 數 值 為[1.388 9, 0.463 0, 0.425 9, 0.5, 0.277 8,0.166 7, 0.148 1, 0.111 1, 0.037 0, 0.092 6]。

此時，所有節點都有了相對重要性分數值，傳播結束。然后，根據相對重要性分數值對節點進行排序。從示例網絡的計算結果可得，對于節點1，相對重要節點可能性的順序應為4, 2, 3, 5, 6, 7, 8,10, 9。

3 實 驗

3.1 數據集

實驗采用了4 個真實網絡數據集，忽略網絡連邊的權重與方向，分別是：

1) 國際航空網絡[20]，節點為國家，邊代表兩個國家有航線，SARS 病毒爆發早期傳播到的國家為重要節點集。

2) 人類蛋白質相互作用網絡PPI[21]，節點代表蛋白質，邊代表蛋白質之間存在相互作用，重要節點集是心臟病基因翻譯的蛋白質。

3) Human 人類蛋白質相互作用網絡[22]，節點代表人類蛋白質，邊代表蛋白質之間存在相互作用，人類蛋白激酶這類蛋白質為重要節點集。

4) Mouse 小鼠蛋白質相互作用網絡[22]，節點代表小鼠蛋白質，邊代表蛋白質之間存在相互作用，小鼠蛋白激酶這類蛋白質為重要節點集。

以上網絡數據集的基本拓撲特征如表1 所示。

表1 網絡基本拓撲特征

其中N表示網絡節點個數，N′表示網絡中重要節點個數，M表示網絡的邊數，K表示網絡平均度，C表示網絡平均聚類系數。

3.2 評價指標

3.3 實證比較

圖2 網絡的AUC 結果

對比不同的算法可知，KSmar 的結果會把距離所有已知重要節點更近的節點的相對重要性分數調高。通過Ksmar 的公式KS=[TP+T2P+····+TkP]也可看出，轉移概率矩陣會給k步內已知重要節點所能到達的節點賦予重要分數，k越小時，所獲得的相對重要分數越高。PPR 是PageRank 的改進方法，在無向圖中，對于度大的節點往往會獲得更多的相對重要性分數。PHITS 是HITS 算法的改進，在無向圖中，已知重要節點是權威節點也是中心節點，因此它往往給已知重要節點的鄰居更高的重要性分數。NLD 則會給每層共同鄰居越多的節點更多的重要性分數。在SARS 網絡中，SARS 爆發的國家與某個國家有越多的航班，該國家成為下一個爆發的國家的可能性更大，這符合NLD 的思想，因此NLD 在SARS 網絡上表現的較好。對于PPI網絡，某一基因與已知致病基因有越多的關聯，該基因為致病基因的概率越大[19]，符合NLD 的思想，因此在PPI 網絡上表現也較好。

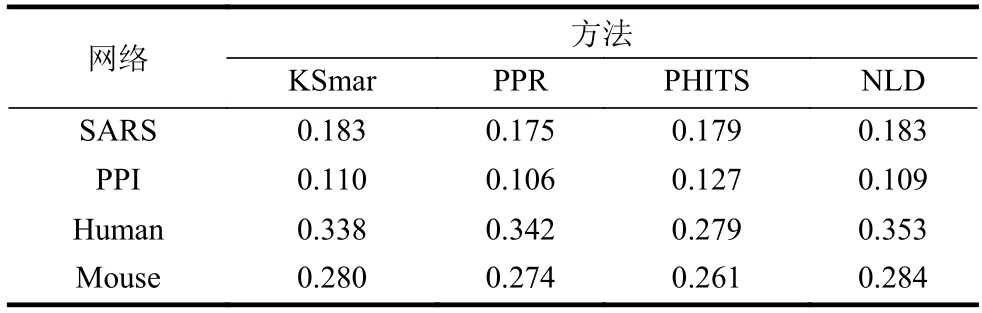
表2 不同的方法在4 個網絡的平均準確率

表3 不同的方法在4 個網絡的平均召回率

從實驗的數據集來看，總體而言，NLD 方法優于其他方法，這說明NLD 在相對重要節點挖掘方面具備準確性與適用性。由于這些方法的優劣一定程度上取決于網絡結構本身，根據網絡結構確定研究方法這也是今后研究的一個問題。

4 結 束 語

本文提出了一種挖掘相對重要節點的方法——NLD，該方法基于與越多已知重要節點關聯，其為相對重要節點的概率越大的假設。本文將NLD與已有的挖掘相對重要節點較好的方法KSmar、PPR、PHITS 進行對比，實驗結果證明NLD 在一定程度優于這些方法。同時，NLD 方法也為網絡信息挖掘提供了新思路。在今后的工作中仍然有很多問題值得深入研究：1) 現有的各種度量網絡中節點相對重要性的指標，比如路徑長度的倒數、介數等，它們之間是否具有一定的聯系。2) 現實世界中雖然很多網絡都可以抽象為復雜網絡，但針對不同網絡設計其適用的挖掘算法仍是亟待研究的。

本文研究工作得到昆明市衛健委項目(2020-09-04-112)的資助，在此表示感謝。