面向高鐵站的熱舒適度和能耗綜合預測

蔣陽升，王勝男，涂家祺，李 莎，王紅軍

（1.西南交通大學交通運輸與物流學院，成都 611756；2.中鐵二院工程集團有限責任公司建筑工程設計研究院，成都 610031；3.西南交通大學經濟管理學院，成都 610031；4.西南交通大學信息科學與技術學院，成都 611756）

0 引言

高鐵站是大量客流聚集的公共場所，其室內環境舒適程度對乘客候車過程中的身心健康和出行狀態具有直接影響。為方便旅客進出，高鐵站進出站口通常處于半封閉半開放狀態，室內外能量交換頻繁，使得高鐵站室內環境舒適度受到諸多因素的影響。為了提高室內環境舒適度，通常高鐵站配置有多聯機及熱交換機等空調系統，但由于高鐵站樓層高、空間跨度大、空氣流動性強以及圍護結構多為玻璃建筑等特點，由此又帶來巨大的能耗。高鐵站作為城市中重要的空間節點，如何借助傳感器技術、數據挖掘技術、機器學習算法等有效感知高鐵站室內環境舒適度特征，獲取影響高鐵站室內環境舒適度和能耗的關鍵因素，并準確預測其變化規律，實現舒適的高鐵站室內環境同時又達到節能降耗的目標是城市計算的新課題［1-2］。

基于此，本文以四川省某高鐵站為研究對象，基于城市計算框架，以表征室內環境舒適度的指標——PMV（Predicted Mean Vote）、空調能耗綜合值為目標，使用6 種機器學習模型進行綜合預測。預測結果能夠用于制定高鐵站智慧溫控系統的控制策略。

本文的主要研究貢獻如下：

1）考慮到高鐵站屬于半封閉公共建筑空間、室內外熱交換頻繁、旅客集聚密度高等特點，針對性地提出影響高鐵站室內環境熱舒適度和能耗的8 個因素——室外溫度、客流密度、多聯機開啟臺數、多聯機設置溫度、熱交換機開啟臺數、室內溫度、室內濕度、室內二氧化碳濃度。

2）為了全面刻畫高鐵站的室內舒適度、能耗的變化規律，本文提出采用傳感器數據捕捉及Energy Plus仿真兩種方式對高鐵站室內外狀態、多聯機及熱交換機等控制單元及熱能傳導環境進行建模，并設計424 種運行工況以充分獲取數據資源。

3）為了描述熱舒適度及能耗與各影響因素的非線性關系，本文提出回歸預測模型選擇框架，通過內嵌6 種機器學習方法，并采用兩個預測性能評價指標以及Friedman 統計量及Iman-Davenport 統計量選擇最佳的高鐵站室內熱舒適度和能耗預測模型。該模型所獲得的預測數據能夠有助于溫控系統主動預判環境狀態參數，為下一階段的溫度控制策略制定提供準確實時的決策場景，避免傳統溫控系統所產生延時的控制策略而影響溫控效果。

1 相關工作

1.1 熱舒適度

20世紀70年代，Fanger［3］通過大量氣候室實驗研究，首次提出了PMV 指標。該指標綜合了空氣溫度、濕度、流速、平均輻射溫度、服裝熱阻以及人體新陳代謝率6 個因素，是迄今為止應用最廣、最全面的熱舒適度評價指標［4］。近年來，有不少國內外學者已經對熱舒適度預測展開研究。主要研究成果可以分為熱舒適度影響因素分析、基于機器學習方法的熱舒適度預測兩類。

1）熱舒適度影響因素分析。該類研究側重于研究環境因素對熱舒適度的影響。Chow等［5］在香港進行了一項以實驗室為基礎的熱舒適性調查，發現人的熱舒適感對空氣溫度和速度很敏感，但對濕度不敏感。劉永頡等［6］利用PMV 方程對典型溫帶地區的熱舒適度影響因素進行分析，最終確定空氣溫度和平均輻射溫度是主要因素。Chan等［7］則通過建立人工神經網絡模型來預測香港室外城市公園的熱舒適性，研究表明，熱感覺是影響熱舒適評價的最重要因素，其次是夏季和冬季的氣溫。為了研究人的熱歷史是否會影響熱舒適度，Jowkar等［8］選取了1 225名在英國居住不到3年的學生以消除在英國適應氣候變化的影響進行實驗，研究表明，有較溫暖熱歷史的人的熱偏好和舒適溫度值高于普通人，為后續研究熱舒適度影響因素提供了更好的參考。

2）基于機器學習方法的熱舒適度預測。該類研究主要采用機器學習相關算法對熱舒適度進行預測。高立新［9］和Yuce等［10］分別利用人工神經網絡來建立智能預測器以及預測室內游泳池的能耗和熱舒適度水平。侯贊等［11］將集成學習運用到了列車的熱舒適度評價上，研究證明，集成學習能提高熱舒適度評價的準確性。Marvuglia 等［12］提出了一種基于神經模糊聯合模型的室內溫度控制器，通過自回歸神經網絡進行室內溫度預測，驅動模糊控制器，從而實現對辦公大樓室內的溫度控制。潘偉強等［13］和楊福邁［14］均利用支持向量機對室內熱舒適度進行評價，前者將結果與反向傳播（Back Propagation，BP）神經網絡和概率神經網絡比較，證明該方法的可行性，后者則提出了針對寒冷地區的熱舒適度評價方法及評價規則，為該地區熱舒適度的評價提供了依據。張玲等［15］和郭彤穎等［16］分別利用改進的粒子群算法和鳥群算法去優化BP 神經網絡，并在此基礎上提出了熱舒適度預測模型，結果證明，改進后的模型比傳統模型預測精度更高、收斂更快。Salamone等［17］在PMV 的基礎上，增加PPD（Predicted Percentage of Dissatisfied）和用戶反饋，作為個人熱舒適的評價指標，并使用機器學習中的分類回歸樹（Classification And Regression Tree，CART）方法來預測用戶的個人資料和熱舒適感知對室內環境的影響。Guenther 等［18］則另辟蹊徑，提出了一種基于高斯過程回歸方法的個性化舒適預測模型。Ji等［19］通過對哈爾濱地區居民樓的實地考察和調查問卷，得出了住戶的舒適度區間，并利用邏輯回歸分析進行驗證，給出了我國嚴寒地區舒適和節能的具體設置溫度，為寒冷地區的節能控制提供了新的參考。Wang等［20］通過分析美國供暖、制冷和空調工程師協會（American Society of Heating，Refrigerating and Air-Conditioning Engineers Ⅱ，ASHRAE Ⅱ）數據，確定了居住者熱體驗的指標，并利用邏輯回歸和支持向量機方法進行熱可接受性和熱偏好的預測。Mui 等［21］為了提高熱舒適模型預測的精確度，提出了兩種貝葉斯更新方法（全局更新和個體更新）用于改進現有的熱舒適模型。Luo 等［22］對比了機器學習中用于預測熱舒適參數的9 種方法，得出隨機森林具有最高的預測準確性。Ngarambe 等［23］將人工智能方法運用到熱舒適度的預測中，力求在不犧牲居住者熱舒適性的情況下優化能源性能。

1.2 空調能耗預測

空調能耗預測一直是暖通空調的熱門研究方向。目前學者對空調能耗預測方法主要分為傳統預測方法和機器學習方法。

1）傳統預測方法。Kikegawa 等［24］和Li 等［25］均考慮了城市熱島效應對夏季建筑空調能耗的可能影響，并建立了建筑物能源使用與城市氣象條件之間的相互作用的多尺度模型。研究指出，估計的空調能源消耗遠大于以往文獻報道的空調能源消耗。楊世忠等［26］對空調冷卻水系統進行節能研究，為空調節能提供了新的研究途徑。Jim［27］和Yuan 等［28］則從建筑的屋頂設計和保溫特性出發，分別在香港和上海兩地展開建筑特性對空調能耗的實地調查，為炎熱夏季城市的綠色屋頂和相關建筑保溫的政策和設計提供了參考。Ma 等［29］則利用組合權重法選擇相似天數對建筑物空調系統能耗進行預測，并采用eQUEST 仿真驗證，結果表明，利用相似天數預測能耗具有較高的準確性。Zhou 等［30］在前人的基礎上，通過分析北京、臺灣、香港和伯克利四個地點在氣候、圍護結構、居住者行為上的差異以及辦公樓的空調能源使用情況，得出了居住者行為影響最大的結論。

2）機器學習方法。為了提高空調能耗預測的準確性，研究者將機器學習應用到了空調的能耗預測上。Atthajariyakul等［31-32］將PMV、二氧化碳濃度和冷熱負荷分別作為熱舒適、室內空氣質量和能耗的參數指標，提出了一種基于神經網絡的PMV 模型用于確定暖通空調系統最佳室內空氣狀態。實驗結果表明，與傳統方法相比，該方法可以有效地實現暖通空調系統室內空氣狀態的實時監測，同時降低能耗。Wei 等［33］提出了一種數據驅動的方法來優化典型辦公設施中暖通空調（供暖、通風和空調）系統的總能耗，并建立了一種綜合設施溫度、相對濕度、二氧化碳濃度的總能量模型，利用改進的多目標粒子群算法對模型做進一步優化，在節能方面取得顯著進展。Zheng 等［34］提出了一種改進的入侵雜草優化算法，以解決使功耗最小化的冷水機組負荷問題，與其他算法相比，該算法可以找到相等或更好的最優解。段冠囡等［35］提出了一種基于GM-RBF（Grey Model-Radical Basis Function）的神經網絡方法對超高層建筑的空調能耗進行預測，并達到較高的預測精度。錢青等［36］則將總能耗分項，利用自回歸和深度置信網絡（Auto-Regression-Deep Belief Network，AR-DBN）建立能耗短期預測模型，與不分項模型相比，該模型預測精度較高。Tran等［37］利用最小二乘支持向量回歸和徑向基函數神經網絡兩種機器學習方法，構建了進化神經機器推理模型。該模型比其他人工智能技術具有更高的預測精度。魏崢等［38］討論了使用機器學習的方法對冷水機組進行控制以降低能耗，優化運行的情況，得出支持向量機（較差）、神經網絡、隨機森林三種算法都有較好的適用性的結論。Zhou 等［39］利用長短期記憶模型預測廣州某高校圖書館的空調系統。結果表明，長短期記憶模型能夠產生更可靠的預測結果。綜上，當前對熱舒適性以及空調能耗的研究有比較豐富的研究成果，但還存在以下不足：

1）大多文獻主要考慮封閉空間的熱舒適度，而高鐵站是一類典型的半封閉半開放的建筑空間，承擔大量客流集散任務，同時室內室外熱交換頻繁，熱舒適會受到室內室外諸多因素的影響，需要針對高鐵站的特點，提煉其室內熱舒適度的影響因素。

2）大多文獻采用某種機器學習算法對熱舒適度或者能耗進行預測。而對于高鐵站而言，由于其半開放的建筑空間特點，各類因素的影響路徑復雜，需要設計多個機器學習算法以確定最佳的預測性能。

3）大多文獻沒有將熱舒適度和能耗結合起來共同預測。由于熱舒適度和能耗存在背反關系，即追求高舒適度會導致高的能耗，如何同時預測兩個目標并協調兩者關系仍待解決。

基于此，本文以四川省某高鐵站為研究對象，提煉了影響其室內舒適度及能耗的多個因素，并建立了熱工環境模型，同時將雙目標（PMV 和能耗）轉化為單目標，并采用了6 種機器學習方法對兩者進行綜合預測。通過大量實驗對比6 種機器學習方法在實驗數據集上的測試效果，最終選出最優預測模型。

2 問題描述

通過大量的文獻調研及實地走訪，本文最終確定影響高鐵站室內舒適度和能耗的因素分別為：多聯機開啟臺數、多聯機設置溫度、熱交換機開啟臺數、客流密度、室外溫度、室內溫度、室內濕度、室內二氧化碳濃度。高鐵站室內熱舒適度評價選用目前廣泛應用的PMV 指標。為了獲取各影響因素與PMV 和能耗之間的復雜非線性關系，本文首先基于現場安裝傳感器進行數據捕捉，然后基于Energy Plus 構建高鐵站的熱工環境模型，并使用傳感器數據對模型進行校正與多輪調試，保證所構建的模型能夠復現高鐵站真實的熱工環境。根據各影響因素的作用范圍，設計不同工況以獲取海量數據，并計算PMV 與能耗值。最后通過6種預測方法（線性回歸、深度神經網絡、嶺回歸、支持向量回歸、貝葉斯嶺回歸、決策樹回歸）進行綜合預測。

2.1 PMV定義

PMV 代表了大多數人在同一環境中的平均冷熱感覺，它根據人體產熱和散熱之間的差值進行計算，該值一般與用戶在房間中的運動和服裝情況及環境情況有關。本文的PMV值采用計算值，具體計算公式如下式（1）［40］所示：

其中：M表示人體能量代謝率，單位為W/s；W表示人體所做的機械功，單位為W/s；Pa表示人體周圍空氣的水蒸氣分壓力，單位為Pa；ta表示人體周圍的空氣溫度，單位為℃；ts表示房間的平均輻射溫度，單位為℃；fcl表示人體著裝后的實際表面積和人體裸身表面積之比，即服裝的表面系數；tcl表示人體外表面溫度，單位為℃；hc表示對流換熱系數，單位為W/s·m2·℃；

本文中將根據所構建的熱工環境中各時刻的狀態參數，如人體周圍的空氣溫度等，依據式（1）對該時刻的PMV 進行計算。

2.2 預測目標函數的建立

為了同時預測PMV 和能耗，并減少預測復雜度，本文將這兩個目標通過線性加權的方式轉化為單目標。根據文獻［41］，本文PMV權重取值為0.6，能耗項權重取值為0.4，以求得熱舒適性和能耗的綜合值為最優。

由于兩個目標的取值與量綱存在較大的差異，為了減少誤差，需要對其進行標準化處理。此外，考慮到PMV 的取值范圍，對其進行絕對值處理。處理之后的預測目標如式（2）所示。

其中：f(x1，x2)為預測目標值；x1為PMV 值；x2為能耗值，為開啟的多聯機和熱回收機的能耗總和；max(|x1|)、min(|x1|)為PMV 值中的最大、最小值；max(|x2|)、min(|x2|)為總能耗中的最大、最小值。

3 高鐵車站熱工環境建模

3.1 高鐵車站調研概況

本次調研選取處于夏熱冬冷地區的四川省某高鐵站為研究對象，該車站為高架車站，站廳層高6 m，吊頂1 m，可大致分為辦公區、候車區、離站區3 個區域，其中候車區的尺寸為74 m×28 m×5 m。該車站共配有5臺多聯機和8臺熱交換機。

本次調研時間為2019年12月31日—2020年1月3日，調研的內容包括高鐵站室內外環境因素的現場實時測試（包含溫度傳感器、濕度傳感器、二氧化碳傳感器的安裝與數據捕捉）、客流密度的實時統計以及站內候車乘客的問卷調查。問卷調查時間間隔為半小時。

3.2 建模數據收集

為了獲得海量數據，本文基于Energy Plus 軟件建立高鐵車站的熱工環境模型，模擬了高鐵車站全年的熱交換與空調能耗情況。該高鐵車站位于四川（北緯30.61°，東經103.68°），建筑朝向為北偏東30°。根據高鐵車站平面圖在sketch up 中建立一個長81.8 m、寬74 m、高5 m 的三維模型；模型中圍護結構構造、建筑結構等參數均嚴格按照該高鐵站實際數據進行設置，各結構布置完成后match 最終模型，從而進行內外墻的識別，確認模型無誤以后，生成IDF 文件，導入EP-Launch進行參數設置及能耗模擬。數據模擬從1月1日開始，12月31日結束，模擬的時間段為7：00—23：00。與此同時根據實地調研結果，對所建模型進行校正與調試。就控制系統開行狀態，本文設計了5+8+40=53種工況，分別為單獨開多聯機、單獨開熱交換機以及多聯機和熱交換機的組合。與此同時，通過文獻調研與實地訪談，設置了8 種多聯機夏季溫度與冬季溫度組合，具體情況如表1。生成了53×8=424種工況，因此，共獲取424×8 760=3 714 240個實例。

表1 多聯機溫度組合Tab.1 Temperature combination of multi-evaporator air conditioners

4 高鐵站熱舒適度和能耗綜合值預測模型

4.1 回歸預測模型的理論

高鐵站熱舒適度與能耗綜合預測是一類回歸問題，因此本文選取深度神經網絡、支持向量回歸、決策樹回歸、線性回歸、嶺回歸、貝葉斯嶺回歸共6 種機器學習方法，建立以PMV和空調能耗綜合值為目標的回歸預測模型，根據回歸預測模型選擇框架最終確定最佳的模型。各模型簡述如下。

1）深度神經網絡（Deep Neural Network，DNN），也稱為多層感知機。在2006 年，Hinton 等［42］利用預訓練方法緩解了局部最優解問題，將隱藏層推動到了7 層，深度神經網絡由此出現。近年來，很多學者也將其應用到回歸問題上。神經網絡中，設置激活函數是σ(z)，隱藏層和輸出層的輸出值為a，第l-1 層共有m個神經元，則對于第l層的第j個神經元的輸出得到式（3）：

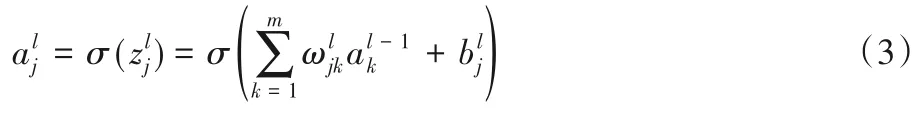
2）支持向量回歸（Support Vector Regression，SVR）。1998年，Haykin［43］將支持向量（Support Vector，SV）學習正式納入機器學習標準方法工具箱，在2002 年Smola［44］對支持向量回歸有了更深入的概述。SVR 作為支持向量機的延伸，設容忍f(x)與y之間有ε的偏差，則SVR問題可以寫為式（4）：

其中：C為懲罰因子，?ε為不敏感損失函數。

3）線性回歸（Linear Regression，LR）［45］。設預測值為則LR問題可以寫為式（5）：

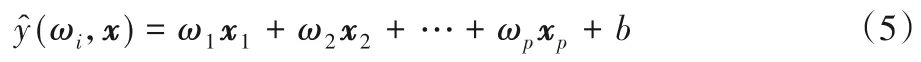
其中：ω=(ω1，ω2，…，ωp)，xi=(xi1，xi2，…，xip)。

4）嶺回歸（Ridge Regression，RR）［46］。通過對系數的大小進行懲罰來解決普通最小二乘問題，其函數可以表示為式（6）：

其中復雜性參數α≥0 控制收縮量：α的值越大，收縮量就越大，因此共線性系數也更大。

5）貝葉斯嶺回歸（Bayesian Ridge Regression，BRR）［47］，具體模型表示為式（7）：

其中：α1、α2、λ1和λ2分別是關于α和λ的γ分布的先驗。

6）決策樹回歸（Decision Tree Regression，DTR）［48］是一種可以用于回歸的決策樹模型，通過非參數分類和回歸方法進行有效的預測。假設X和Y分別為輸入和輸出變量，給定訓練數據集為D={(x1，y1)，(x2，y2)，…，(xN，yN}) 其中xi=為輸入實例（特征向量），n為特征個數，i=1，2，…，N，N為樣本數量。

對特征空間的劃分采用啟發式方法，每次劃分逐一考察當前集合中所有特征的所有取值，根據平方誤差最小化準則選擇其中最優的一個作為切分點。如對訓練集中第j個特征變量x(j)和它的取值s，作為切分變量和切分點，并定義區域R1(j，s)={x|x(j) ≤s}和R2(j，s)={x|x(j) ＞s}，為找出最優的j和s，求解式為式（8）：

找出使要劃分的兩個區域平方誤差和最小的j和s。其中，c1、c2為劃分后兩個區域內固定的輸出值，方括號內的兩個min 意為使用的是最優的c1和c2，也就是使各自區域內平方誤差最小的c1和c2，易知這兩個最優的輸出值就是各自對應區域內y的均值，所以式（8）可寫為式（9）：

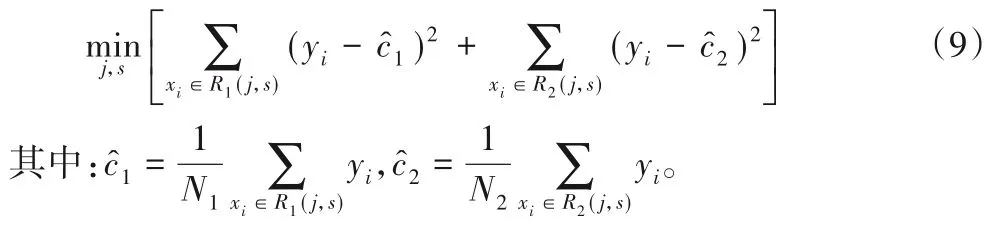
找到最優的切分點(j，s)后，依次將輸入空間劃分為兩個區域，接著對每個區域重復上述劃分過程，直到滿足停止條件為止。這樣就生成了一棵決策回歸樹。本研究通過對比6 種機器學習方法對仿真數據預測的準確性，最終選出適合于本研究的最優回歸預測模型。

4.2 熱舒適度和能耗綜合預測模型選擇框架

為了選擇合適的模型對高鐵站室內熱舒適度和能耗進行準確預測，本文設計了回歸預測模型選擇框架，具體過程如圖1所示。

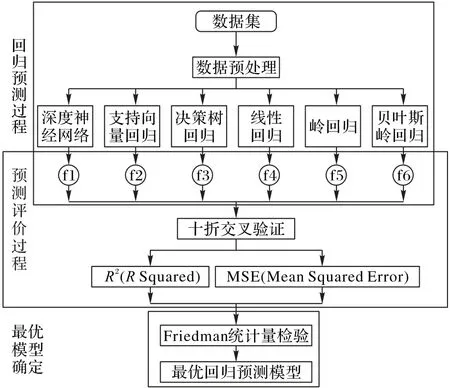
圖1 回歸預測模型選擇框架Fig.1 Selection framework of regression prediction model

5 實驗與結果

5.1 數據預處理

將數據集輸入模型進行訓練前，需要對其進行預處理，具體步驟包括：

步驟1 數據劃分。按月份將數據分為12組。

步驟2 缺失值與異常值的處理。刪除數據集中缺失能耗的數據及異常值。

數據預處理后的數據集如表2所示。

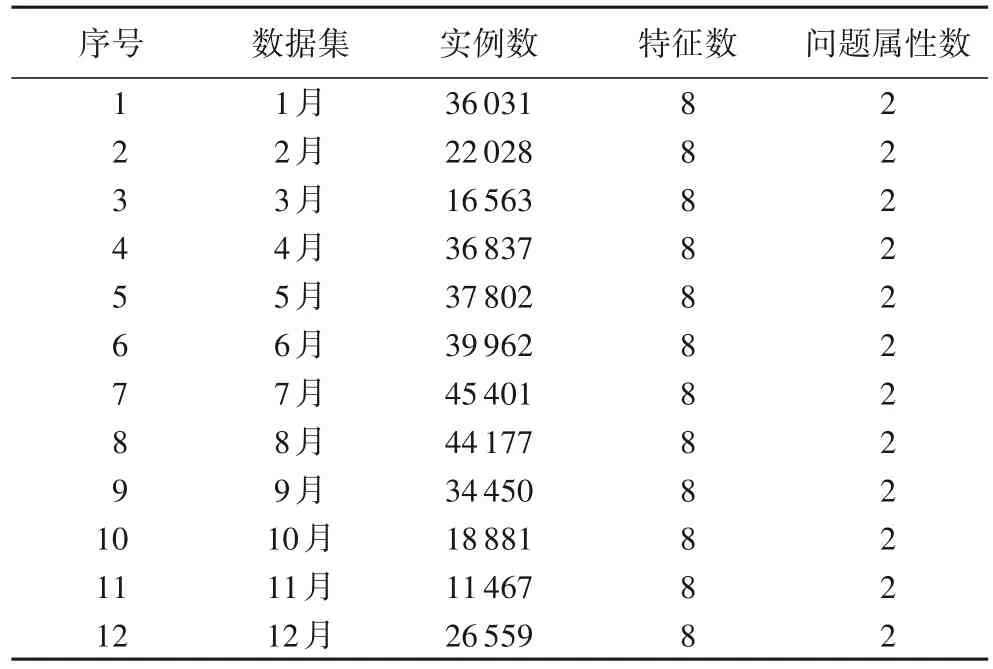
表2 實驗數據集的樣本、特征、問題屬性數量Tab.2 Numbers of instances，features and problem properties of experimental datasets

表2 中的問題屬性即為本研究的目標函數，包括PMV 值和總能耗值兩種屬性。

5.2 評價指標

本文選取均方誤差（Mean Squared Error，MSE）［49］和擬合優度（RSquared，R2）［50］兩個指標來評價模型預測性能。

MSE標準計算如式（10）所示：

其中：n為測試樣本的數量，yi表示PMV 和能耗綜合值的實際值表示回歸模型的預測值。MSE的值越小，代表預測的準確率越高。

R2標準計算如式（11）所示：

為了進一步測試算法準確性，本文使用十折交叉驗證對6 種算法進行測試，即將數據集分成10 份，依次將其中9 份作為訓練數據，1份作為測試數據，進行實驗。將10次結果的正確率（或差錯率）的平均值作為對算法精度的估計。

為了檢驗不同算法的差異，本文使用Friedman統計量，其定義如下：

5.3 實驗參數設置

本研究的部分模型依賴超參數的選擇，為了保證實驗的嚴謹性，在測試模型的過程中，根據超參數不同設置對模型進行調參優化操作。因線性回歸不需調參，本研究對其他5 個模型的超參數進行調試優化，具體過程如下。

針對嶺回歸中的超參數α，首先設置取值范圍為［0，1 000］，步長為100進行調參。實驗表明當α取值為100，MSE的值達到最小0.005 6。隨之將α取值范圍調至［50，150］，步長為10；取值范圍為［80，100］，步長為2以及取值范圍為［85，95］，步長為1 進行參數微調。最終確定當α=90 時MSE的值最小。

對于支持向量機回歸，本實驗主要調節懲罰系數C的設置。設置C的取值范圍為［0.5，1.5］，步長為0.1 進行實驗。結果表明當C=1.1時，MSE的值達到最優，為0.012 7。

決策樹回歸主要通過min_samples_split參數來控制葉節點上的樣本數量。設置min_samples_split的取值范圍為［2，15］，步長為1進行參數測試。結果表明，當min_samples_split=11時，MSE最優，為0.002 0。

貝葉斯嶺回歸主要調節超參數α1、α2，它們是α關于γ分布的先驗，默認α1=α2=10-6。本研究測試了α1、α2分別取值10-7、10-6、10-5下的9 種組合，最終測試結果表明α1、α2的變化對MSE值不產生影響。

深度神經網絡的效果主要依賴網絡層數的選擇，本研究測試了1）8→16→18→12→1；2）8→24→12→1；3）9→16→18→24→12→1 三種不同層數、不同神經元個數的網絡結構，最終測試結果顯示第1）種優于其后兩者，MSE為0.011 3，故選擇1）結構構建模型。

5.4 實驗與結果

本文所選取的6 種機器學習算法，其MSE和R2結果以及測試時間如圖2～4及表3～5所示。

圖2 MSE標準的十折交叉驗證結果對比Fig.2 comparison on MSE

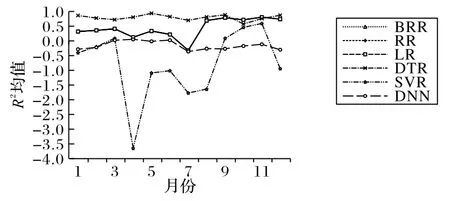
圖3 R2標準的十折交叉驗證結果對比Fig.3 Ten-fold cross-validation result comparison on R2

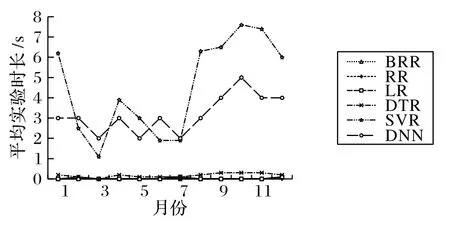
圖4 十折交叉驗證結果的實驗時間對比Fig.4 Ten-fold cross-validation result comparison on experimental time

由圖2～4可知，不論是在MSE標準的十折交叉驗證下，還是在R2標準的十折交叉驗證下，6 種算法中，DTR 的預測性能最佳。由表3～5 可知，6 種回歸模型中，DTR 的綜合預測性能最佳。在MSE方面，12 個數據集中有11 個DTR 都取得了最小值。在所有的數據集中，DTR的平均MSE最低，為0.002 2。其余算法的平均MSE從小到大依次為0.005 6（LR），0.005 6（RR），0.005 6（BRR），0.016 1（SVR），0.025 2（DNN）。在R2方面，12個數據集中有10個數據集DTR都取得了最大值。在所有的數據集中，DTR 的平均R2最大，為0.793 8。在第5 個數據集達到了最大R2（0.937 2）。其余算法的平均R2從大到小依次為 0.431 6（RR），0.431 1（BRR），0.431 0（LR），-0.159 0（DNN），-0.789 8（SVR）。在運行時間方面，DTR 的平均運行時間0.175 0 s，也大大優于DNN（3.166 7 s）。

表3 6種機器學習算法的均方誤差及秩次Tab.3 Mean square error and rank for six machine learning methods

為了檢驗6 種機器學習算法的總體性能，本文使用Friedman 統計量進行假設檢驗。6 種算法在各個數據集上MSE的平均秩次分別為5.750 0，5.250 0，2.916 7，2.916 7，2.916 7，1.250 0。MSE的Friedman統計量為：

6 種算法在各個數據集上R2的平均秩次分別為5.583 3，5.416 7，3.166 7，2.916 7，2.416 7，1.500 0。R2的Friedman 統計量為：

本次對比實驗基于6個算法，12個數據集，FF服從于自由度為6-1=5 和（12-1）（6-1）=55 的F 分布。由F（5，55）分布計算FFMSE、FFR2所對應的p的值分別為9.486 26E-19、7.205 94E-17，所以在高顯著性水平下拒絕原假設，綜合圖2～4結果可知DTR 算法在高鐵站熱舒適度和能耗預測的準確率均優于其他對比算法。

表4 6種機器學習算法的擬合優度及秩次Tab.4 R2 and rank for six machine learning methods

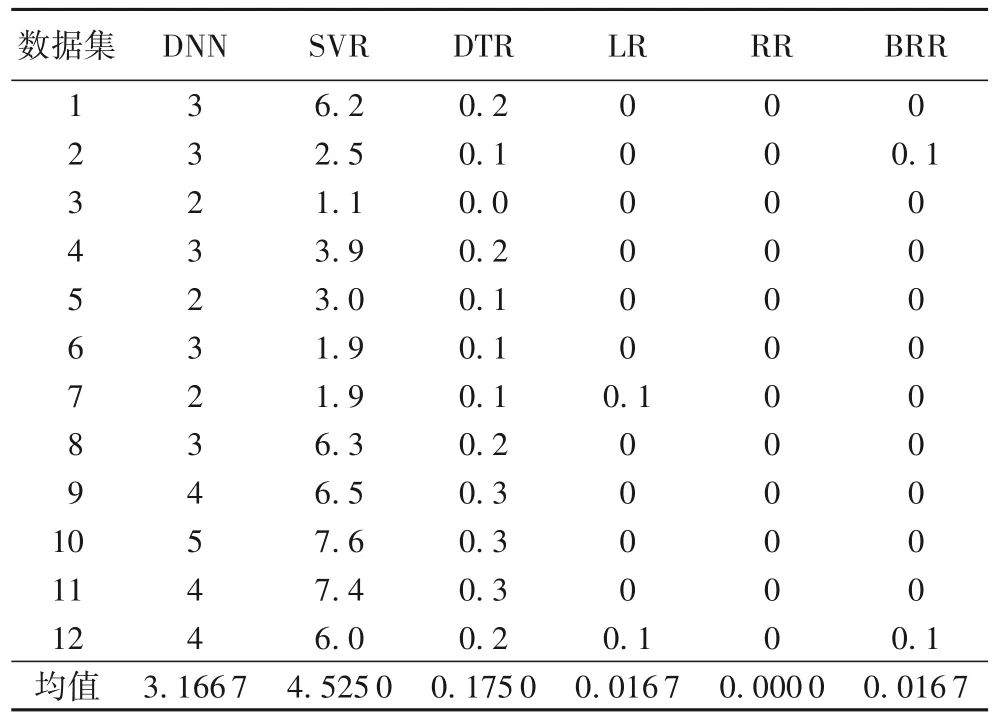
表5 均方誤差及R2的實驗時長比較 單位：sTab.5 Comparison of experimental time for MSE and R2 unit：s

6 結語

對于高鐵站熱舒適度和能耗的預測研究，對實現高鐵站智能溫控，改善人們的生活環境和節能減耗具有重要意義。

本文通過現場傳感器數據捕捉及Energy Plus平臺對四川省某高鐵候車廳室內外狀態、多聯機及熱交換機等控制單元及熱能傳導環境進行建模，獲取影響高鐵站室內熱舒適度和能耗的8 個因素：室外溫度、客流密度、多聯機開啟臺數、多聯機設置溫度、熱交換機開啟臺數、室內溫度、室內濕度、室內二氧化碳濃度。通過傳感器數據對所建熱工模型進行校正與調試，并運行424種工況，生成3 714 240個實例。為了獲取熱舒適度及能耗的變化規律，本文基于回歸預測模型選擇框架，運用6 種機器學習方法（深度神經網絡、支持向量回歸、決策樹回歸、線性回歸、嶺回歸、貝葉斯嶺回歸）對高鐵站室內熱舒適度及能耗進行綜合預測。通過大量實驗可知，6 種機器學習算法中，決策樹回歸模型預測能夠在較短的時間內獲得最佳的預測性能。相比其他算法，決策樹回歸模型在所有的數據集里，其平均R2最大，為0.793 8，平均MSE最低，為0.002 2。綜上，決策樹回歸能夠較好地反映高鐵站室內熱舒適度和能耗的變化規律，可以為室內環境的智慧溫控系統的控制和節能減耗提供決策支持。