低頻波動條件下單相流體多孔介質(zhì)滲流規(guī)律

陳濤濤，王 強，劉 甜

（1.西安石油大學(xué)石油工程學(xué)院，陜西西安 710065；2.陜西省油氣田特種增產(chǎn)技術(shù)重點實驗室，陜西西安 710065）

低頻水力脈沖采油技術(shù)，是一種物理法采油技術(shù)。其工藝是將用表面活性劑處理過的水或輕質(zhì)油經(jīng)多次瞬間升降壓注入地層，從而恢復(fù)、增強油層滲流能力[1]。在低頻水力脈沖波的激勵作用下，儲層將產(chǎn)生微裂縫，油氣滲流通道增多，絕對滲透率提高。低頻脈沖波作用于地層，其沖擊作用可以提高水驅(qū)波及系數(shù)，進而提高最終采收率。同時，由于注入地層的脈沖液與油、水及巖石密度不同，可以降低原油黏度及巖層水的表面張力，使原油更易流動。

室內(nèi)實驗已證明低頻波動采油技術(shù)在一定條件下可以提高油藏最終采收率，該技術(shù)在油田現(xiàn)場也已廣泛應(yīng)用，但因其背后的物理過程非常復(fù)雜，有關(guān)學(xué)者提出了各種假設(shè)來揭示提高采收率的實際原因。目前普遍接受的觀點是，脈沖波為油分子提供能量，以克服毛細管力，從而增加原油的流動性。毛管壓力的降低導(dǎo)致界面張力減小，使采出更多的油成為可能。目前對低頻水力脈沖采油技術(shù)理論模型的研究主要有兩大方向：（1）不考慮固體與流體的耦合作用，通過較為簡單的假設(shè)與近似，將波動壓力直接疊加到運動方程中；（2）考慮較為復(fù)雜的流-固耦合關(guān)系，建立方程并進行數(shù)學(xué)求解。

本文以波動采油技術(shù)作用機理、多孔介質(zhì)彈性波傳播模型、常規(guī)滲流模型為基礎(chǔ)，建立低頻波動條件下單相流體滲流模型。通過對儲層物性參數(shù)的敏感性分析，來揭示低頻波動激勵下飽和單相流體多孔介質(zhì)滲流規(guī)律變化和儲層物性特征。

1 簡化的波動滲流模型

簡化的波動滲流模型忽略流-固耦合作用，通過較為簡單的假設(shè)與近似，直接將波動壓力疊加到滲流運動方程中。

1.1 模型假設(shè)條件

多孔介質(zhì)中脈沖流體運動模型的推導(dǎo)，有以下假設(shè)條件：

（1）不考慮固體與流體的耦合作用；（2）假設(shè)地層中的流體是單相的；（3）無波動條件時，地層中流體具有一定的滲流速度；（4）假設(shè)同一截面上的質(zhì)點振動速度、初始相位相同。

1.2 波動滲流模型的建立

脈沖波為簡諧波，其一般振動方程為：

式中：A-初始振幅，cm；ω-振動頻率，Hz；t-振動時間，s；x-波傳播的距離，cm；u-波在介質(zhì)中的傳播速度，cm/s；φ-初始相位。

在多孔介質(zhì)中傳播時，低頻脈沖波存在一定的能量損耗，引入耗散系數(shù)e-αx可表征脈沖波在多孔介質(zhì)的振動方程[2]：

式中：α-衰減系數(shù)。

同一振源產(chǎn)生的n 列波具有相同的振幅和相位，將n 列波疊加后，其振動方程為：

將n 列波疊加后，質(zhì)點的振動速度為：

將無波動時多孔介質(zhì)中流體的流速與式（4）得到的振動速度相加，可得波動條件下，流體在多孔介質(zhì)中的流速：

式中：v-流體在波動條件下的流速，μm/s；v1-流體在無波動條件下的流速，μm/s。

保持其他參數(shù)不變，改變公式（5）中單個參數(shù)，可得到時間、距離、波動頻率和振幅與滲流速度的相對關(guān)系。

波動條件下單相流體在地層中傳播的動力學(xué)理論分析表明，通過較為簡單的假設(shè)與近似，將儲層流體原來的流速與n 列波疊加后的振動速度相加[3]，可得到脈沖波激勵下地層流體速度，從而得到低頻波動激勵下地層流體的流速方程。文中波動條件下的滲流方程可從理論上揭示不同參數(shù)導(dǎo)致滲流速度的改變，為脈沖波采油技術(shù)在現(xiàn)場的應(yīng)用奠定理論基礎(chǔ)。

模型不足之處在于，未充分考慮初始滲流狀態(tài)、儲層物性特征、波動激勵下的流-固耦合等[3，4]，只是將波動壓力疊加至常規(guī)滲流方程。

2 復(fù)雜的波動滲流流-固耦合模型

流-固耦合是一些可動或可變形的結(jié)構(gòu)與內(nèi)部或周圍流體的相互作用。其引起的流固相互作用和相互影響既可以是穩(wěn)定的，也可以是振蕩的。在振蕩相互作用中，固體結(jié)構(gòu)中引起的應(yīng)變使其移動，從而應(yīng)變源減少，并且只有在重復(fù)該過程的情況下，結(jié)構(gòu)才恢復(fù)到原來的狀態(tài)。

通常，流-固耦合問題和多物理場問題往往太過復(fù)雜，無法分析求解，因此常需要通過實驗或數(shù)值模擬對其進行求解。盡管計算流體動力學(xué)和計算結(jié)構(gòu)動力學(xué)領(lǐng)域中的研究仍在進行中，但是這些領(lǐng)域的成熟使得對流-固耦合進行數(shù)值模擬變得可能。

2.1 模型假設(shè)條件

飽和單相流體的多孔介質(zhì)彈性波傳播模型的推導(dǎo)，有以下假設(shè)條件：（1）彈性波傳播區(qū)域外的多孔介質(zhì)，不考慮其流-固耦合作用；（2）巖石本身彈塑性不隨應(yīng)力變化，多孔介質(zhì)為完全彈性且本構(gòu)關(guān)系不變；（3）儲層裂縫不發(fā)育，忽略固體顆粒影響；（4）多孔介質(zhì)為均質(zhì)砂巖，飽和單相可壓縮流體；（5）忽略熱彈性造成的波動能量耗散；（6）彈性波波長遠大于孔隙單元尺寸。

2.2 彈性波傳播模型的建立

根據(jù)上面的假設(shè)條件，可建立相應(yīng)數(shù)學(xué)模型來描述低頻脈沖波作用下飽和單相流體多孔介質(zhì)滲流規(guī)律。分析以Biot 模型為代表的飽和單相流體孔隙介質(zhì)彈性波傳播理論模型，建立考慮儲層流-固耦合作用的動力學(xué)模型，可用于波動采油對儲層滲流影響的敏感性分析[4]。通常需要用到的物理原理包括：運動方程、連續(xù)性方程、狀態(tài)方程，再結(jié)合輔助方程和初邊條件，可推導(dǎo)低頻脈沖波作用下飽和單相流體多孔介質(zhì)滲流模型。

式中：μ、λ、α-拉梅系數(shù)；u、w-固體、液體相對位移，μm；ξ-相對膨脹比；e-巖石體應(yīng)變，無因次；b-耗散因子，kg/（m3·s）；M-新定義的參數(shù)，MPa；ρ-多孔介質(zhì)密度，kg/m3；ρf、ρs-表示液體、巖石骨架的密度，kg/m3；η-流體黏度，mPa·s；φ-多孔介質(zhì)孔隙度；k-多孔介質(zhì)滲透率，10-3μm2。

考慮脈沖激勵條件下孔隙度與流壓變化較小，忽略體力項參數(shù)，可得飽和單相流體多孔介質(zhì)滲流的控制方程為：

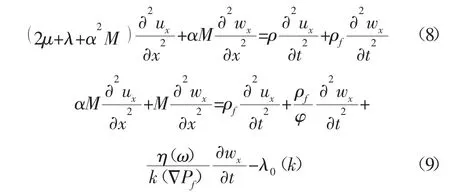
通過對控制方程（8）、（9）進行Laplace 變換，得到Laplace 變換域內(nèi)定壓或定流量開采的液體位移和固體位移解[5]，并利用DURBIN 逆變換得到原問題的解。然后通過MATLAB 編程，最終得到低頻波動條件下多孔介質(zhì)中液體位移、固體位移、孔隙度、孔隙壓力的變化。

上述模型主要考慮流-固間相對關(guān)系，為多孔介質(zhì)中滲流規(guī)律變化和儲層物性變化分析奠定基礎(chǔ)，模型結(jié)果可用于低頻波動采油技術(shù)或其他波動激勵下的油藏增產(chǎn)措施。

3 結(jié)論及發(fā)展

研究單相不可壓縮流體的穩(wěn)定滲流規(guī)律時，必須先從連續(xù)性方程、狀態(tài)方程和達西方程出發(fā)，導(dǎo)出基本微分方程式，然后再結(jié)合邊界條件進行數(shù)學(xué)求解[6]。對于形狀規(guī)則的均質(zhì)地層；可以用復(fù)變函數(shù)的方法求得壓力分布和運動規(guī)律，也可以用無窮乘積方法解決這一問題。對于任意形狀、不等厚非均質(zhì)油氣藏中的滲流問題，目前只能用數(shù)值積分方法來求解。

（1）低頻波動采油技術(shù)以較低的成本增加了產(chǎn)量，該方法適用于所有油藏，無論地層類型如何，對非均質(zhì)油藏都能有效地采出剩余油。它還可以與其他開采技術(shù)聯(lián)合使用，以提高區(qū)域波及效率。

（2）目前對低頻水力脈沖采油技術(shù)理論模型的研究主要有兩大方向：一是不考慮固體與流體的耦合作用，通過較為簡單的假設(shè)與近似，將波動壓力直接疊加到運動方程中；二是考慮較為復(fù)雜的流-固耦合關(guān)系，建立方程并進行數(shù)學(xué)求解。

（3）研究表明，脈沖波激勵下儲層流體速度可由儲層流體初始流速與n 列波疊加后的振動速度相加得到。

（4）以Biot 模型為基礎(chǔ)的飽和單相流體孔隙介質(zhì)彈性波傳播理論模型，可從理論上解釋波動采油對儲層滲流的影響。

數(shù)學(xué)模型建立時，未充分考慮儲層物性參數(shù)受彈性波振動的影響，彈性波作用對多孔介質(zhì)單相滲流影響的部分微觀方面無法準確體現(xiàn)。因此，開展相關(guān)數(shù)值模擬研究，有助于準確揭示低頻波動采油技術(shù)對低滲透油藏孔-滲參數(shù)的影響。