基于雙鏈量子遺傳優化的分類規則挖掘算法*

張宇獻，陳向文，錢小毅

(沈陽工業大學 a. 電氣工程學院，b. 信息科學與工程學院，沈陽 110870)

基于規則的分類系統(rule-based classification systems，RBCSs)由若干條包含數值型前件的規則構成，通過對訓練樣本的學習實現規則挖掘，根據規則與新樣本的匹配程度進行分類.與其他分類系統相比，基于規則的分類系統除了可同時處理專家知識、數學模型和經驗數據等多源信息，其輸出結果還具有極強的可解釋性，給決策者或操作者提供了更好的決策依據，因此，系統被廣泛應用于縱多領域[1-2].

文獻[3]提出一種基于小生境遺傳算法的規則提取算法，從規則編碼、適應度設計、搜索策略三個方面做了討論和分析，但算法耗時長，計算量大，同時種群多樣性差；文獻[4]通過改進基因表達式編程(GEP)提出兼顧規則一致性增益和完備性的適應度函數，但是GEP采用多基因染色體模式解決問題時，染色體中基因數目不好控制；文獻[5]提出一種基于粗糙集增量式規則自動學習的方法獲取分類規則，避免了繁瑣的重訓練過程，但此方法不能準確找到規則進行樣本分類且更新過程繁瑣；文獻[6]通過采用自適應信息素更新和更換啟發式函數的蟻群算法(ACO)實現分類規則的挖掘，精度有所提升，但是算法收斂速度緩慢，且易陷入局部最優解；文獻[7]在ACO算法的基礎上提出了一種自適應蟻群算法，通過動態調整決定性選擇概率和波動系數值，加快ACO收斂速度，但搜索空間有限且魯棒性較差；文獻[8]將粒子群算法(PSO)用于分類規則挖掘，通過改變粒子群的位置和速度以及適應度評價指標減少分類規則數目和縮短運行時間，但此方法易早熟收斂，且尋優能力差.

上述基于規則的分類算法中普遍存在著全局搜索能力不強、魯棒性和種群多樣性較差的問題.本文提出基于雙鏈量子遺傳的分類規則挖掘算法(DCQGA-CRM)，該算法以雙鏈量子遺傳算法為框架，采用雙鏈量子和目標函數梯度信息進行分類器構建，將量子比特的兩個概率幅作為基因位描述可行解，利用量子旋轉門加快規則挖掘收斂速度，通過量子非門對規則前件進行變異.

1 基于規則的分類系統

分類系統由多條分類規則表示，通過分析訓練樣本數據構建分類系統模型，進而檢驗分類精確度，實現對未來采集樣本數據分類.每個數據樣本可看作由條件屬性和類標簽(目標屬性)組成，其表達式為

Vq=(vqj，gl)

(1)

式中：vqj為第q個樣本第j個條件屬性值，q=1，2，…，N，j=1，2，…，n；gl為第l類標簽，l=1，2，…，c.

通常用具有高層次性和象征性的If-Then分類規則來搭建分類器模型，典型的分類規則形式為

Rk：ifA1=xk1and … andAj=xkjthenCk=gkl

(2)

式中：Aj為第j個條件屬性；Ck為第k條規則所屬類別；gkl為第k條規則第l類標簽.

精確度是評價基于規則分類器的重要指標，分類精度越高，表明分類器分類效果越好.本文用正確分類樣本數占分類樣本總數的比例表示精確度.

分類問題中樣本正確分類數目確定過程如下：1)計算樣本數據與分類規則前件差；2)選擇前件差最小值作為樣本適用規則；3)對樣本分類，設樣本正確分類數目初值為零，比較樣本類標簽gl和分類規則類標簽gkl是否相等.

采用測試樣本對分類模型進行檢驗，精度越高，表明搭建分類器模型越好，進而對新測試樣本數據進行分類，賦予類標簽.

2 基于DCQGA的分類規則挖掘

量子遺傳算法(QGA)是在遺傳算法的基礎上，將量子理論引入到其中的智能優化算法.本節將雙鏈量子與分類規則挖掘相結合，主要過程包括量子位實數編碼、解空間變換、量子旋轉門操作和量子非門變異幾個部分.

2.1 量子位實數編碼

DCQGA-CRM采用雙鏈量子位實數編碼方式產生分類規則，每個個體包含上下兩條基因鏈，每條基因鏈對應優化問題的一個分類規則.在種群規模一定的條件下，通過雙鏈量子位實數編碼方式增加種群多樣性，加倍搜索空間.

QGA以充當信息存儲單元的雙態量子比特系統為基礎，用量子比特表示染色體，兩個量子態的線性疊加態表示一個量子位，其形式為

|φ〉=γ|0〉+β|1〉

(2)

式中，γ、β為量子比特的概率幅，滿足歸一化條件.考慮歸一化約束性，用概率幅編碼，則DCQGA-CRM雙鏈編碼方式表示為

(3)

式中，costij、sintij為第i個種群、第j個量子位的兩個概率幅值.

2.2 解空間變換

雙鏈量子實數編碼產生分類規則的概率幅在[-1，1]之間，與原始樣本數據存在差異.利用解空間變換將量子位概率幅轉換為指定范圍內相對應實數集，便于分類規則與樣本對比.由于每條染色體含有2m個量子位的概率幅，可利用線性變換將m維單位空間Im=[-1，1]轉換到實數解空間.令aj表示第j個量子位下限值，bj表示第j個量子位上限值，則相應解空間變換為

(4)

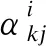
2.3 量子旋轉門轉角方向

量子旋轉門操作的作用是促使染色體上每個基因位概率幅值收斂到預先設定幅值，從而使其收斂到全局最優解.量子旋轉門表達式為

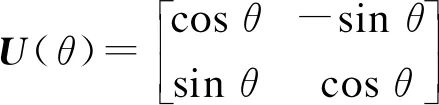
(5)

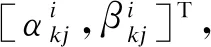
(6)

量子旋轉門更新過程中，旋轉角方向和大小是根據預先設定調整策略確定的.量子旋轉門只改變相位大小，不改變量子位長度.量子基因位幅值對收斂速度造成直接影響，其值一般設置為0.001π～0.1π.

2.4 量子旋轉門轉角大小

量子旋轉門轉角大小更新策略為：目標函數在搜索點處梯度較大，即所處搜索過程較陡時，適當減小步長，避免越過全局最優解；反之，適當增大步長，加速其搜索過程，盡快搜尋到全局最優解.根據搜索點處目標函數梯度變化確定搜索點處步長，即

(7)

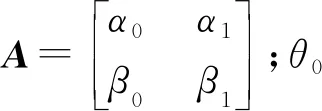
2.5 量子變異

依據變異概率選擇最優染色體，對染色體量子位施加量子非門操作，通過改變量子位概率幅使兩條基因鏈上量子位同時得到變異，其變異過程為

(8)

基于雙鏈量子遺傳優化的分類規則挖掘算法流程圖如圖1所示.

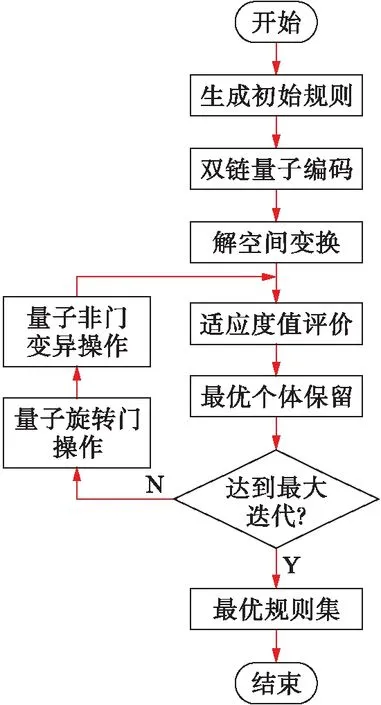
圖1 DCQGA-CRM算法流程圖Fig.1 Flow chart of DCQGA-CRM algorithm

3 實驗與結果分析

本文選取UCI數據庫中9個數據集對算法的分類精度和魯棒性進行對比分析.首先將所提算法與兩種基于規則的分類算法(Michigan算法和Pittsburgh算法)進行對比分析.在此基礎上，在訓練集中添加類噪聲，將所提算法與Michigan算法[9]、Pittsburgh算法[10]、C4.5算法[11]和BP神經網絡[12]進行對比，驗證所提算法的噪聲容忍度.

3.1 數據集與算法評價指標描述

數據集具體描述如表1所示，其中，#Ex.為樣本數，#Atts.為屬性數，#Class.為類別數.

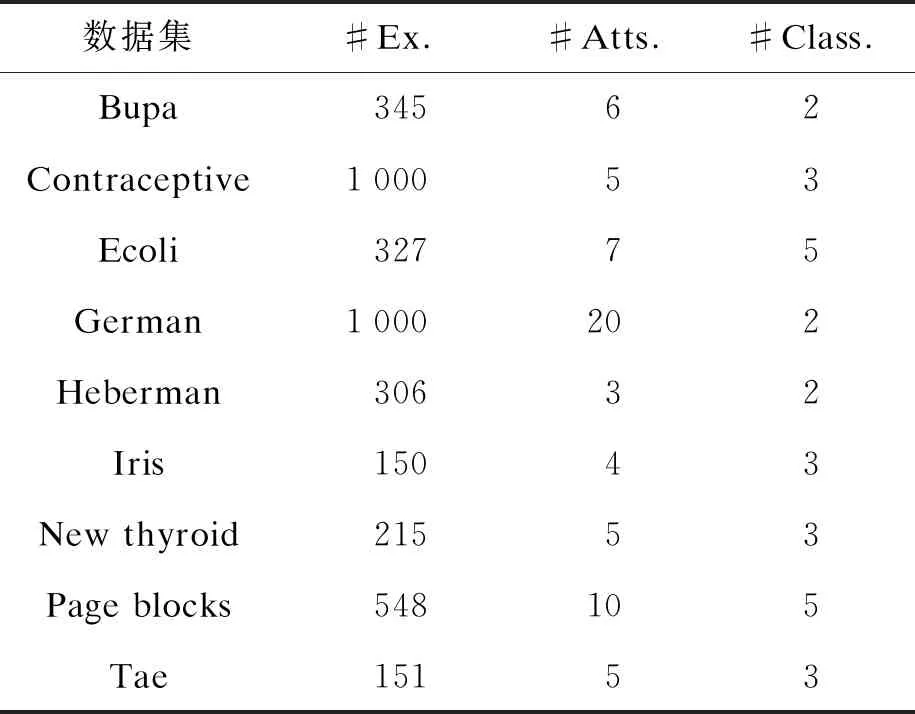
表1 UCI數據集描述Tab.1 Description of UCI datasets

本文采用樣本正確分類數占樣本總數的比例來進行描述分類精度；引入相對損失精度RLA來描述魯棒性優劣，其定義為

(9)

式中：e0%為原始數據集下測試分類精度；ex%為噪聲水平下測試分類精度.

為驗證所提出的DCQGA-CRM與其他分類算法相比具有顯著性能，采用Wilcoxon符號秩檢驗[9]進行顯著性測試.比較檢驗概率p值與顯著水平α的大小，判斷兩個算法預測階段平均值與各自所代表的總體差異是否顯著，本文選取顯著水平α=0.05.本實驗采用5折交叉驗證方式進行算法性能驗證，即將數據集隨機分成5等份，選取其中的4份作為訓練樣本集，其余部分作為測試樣本，實驗結果選取5次運行結果平均值和標準差.

3.2 分類精度分析

將本文算法與Michigan算法和Pittsburgh算法進行分類精度比較分析，各算法參數設置如表2所示.

表2 不同算法參數設置Tab.2 Parameters settings of different algorithms

表3為DCQGA-CRM與Michigan算法和Pittsburgh算法分類精度對比，分別記錄了各算法對9組數據集的訓練精度(eTr)與測試精度(eTst)結果，精度值后面的數值為分類精度的標準差.由表3可以看出，在9個數據集的實驗結果中，DCQGA-CRM在測試結果的分類正確率明顯高于其他兩種對比算法.將DCQGA-CRM與Michigan算法、Pittsburgh算法的Wilcoxon符號秩檢驗進行對比，本文所提出算法得到的檢驗概率p值均小于0.05，說明本文提出的DCQGA-CRM與Michigan算法、Pittsburgh算法相比，分類性能有顯著性提高.

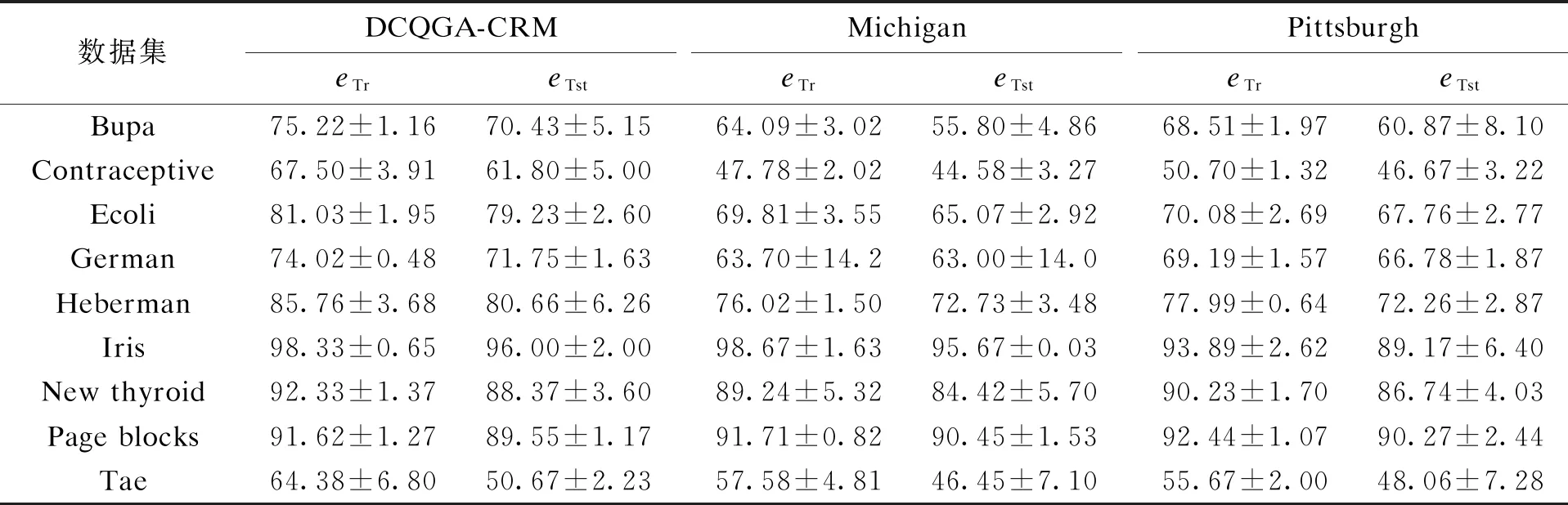
表3 DCQGA-CRM與其他分類算法分類精度對比Tab.3 Comparison in classification accuracy between DCQGA-CRM and other classification algorithms %

表4為本文所提算法與其他算法在分類精度實驗中數據集單次運行的時間對比，其中，Pittsburgh算法和本文提出算法中的單個個體均代表一個分類器，因此，單次運行的時間要高于以單條規則為優化對象的Michigan算法，但本文所提算法采用量子旋轉門策略提高了單次迭代的運行速度.

表4 各算法運算時間對比Tab.4 Comparison of operation time among different algorithms s

3.3 分類魯棒性分析

通過向訓練數據集中加入類噪聲來分析DCQGA-CRM的噪聲容忍度.采用不同類噪聲水平(noise level，NL)測試其預測精度，并通過相對損失精度RLA分析算法在類噪聲作用下的噪聲容忍度.

本實驗還選擇了對類噪聲容忍度較強的C4.5算法和BP神經網絡進行比較分析.圖2為噪聲水平分別取NL=10%，20%，30%，40%和50%時不同算法對樣本數據集的分類精度.在大多數數據集情況下，DCQGA-CRM類噪聲容忍度優于其他算法.

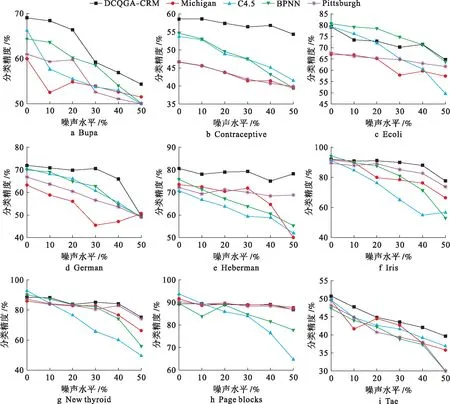
圖2 不同噪聲水平下DCQGA-CRM與其他算法分類精度對比Fig.2 Comparison of classification accuracy between DCQGA-CRM and other algorithms under different noise levels

本文給出了類噪聲分別為10%、30%、50%時的RLA值，如表5所示.表5中，(·)值表示同一噪聲水平下各算法的RLA值排名，Av.Rank表示各算法在9個數據集測試中的平均排名.從表5中可以看出，DCQGA-CRM的RLA在大多數情況下小于其他對比分類算法，擁有良好的噪聲容忍度.

4 結 論

本文針對智能優化分類規則挖掘算法中分類精度低及噪聲容忍度差等問題，提出一種DCQGA-CRM算法，以基于規則的分類系統為框架，采用雙鏈量子實數編碼增加搜索空間多樣性，通過量子旋轉門操作和量子非門進行策略更新，利用目標梯度函數避免陷入局部最優解.實驗利用UCI數據庫中9個數據集，將所提出的DCQGA-CRM與對比分類方法相比，實驗結果表明，DCQGA-CRM具有較高分類精度和噪聲容忍度.相對精度損失RLA和Wilcoxon符號秩檢驗表明，DCQGA-CRM與其他分類方法相比，噪聲容忍度有顯著性提高.

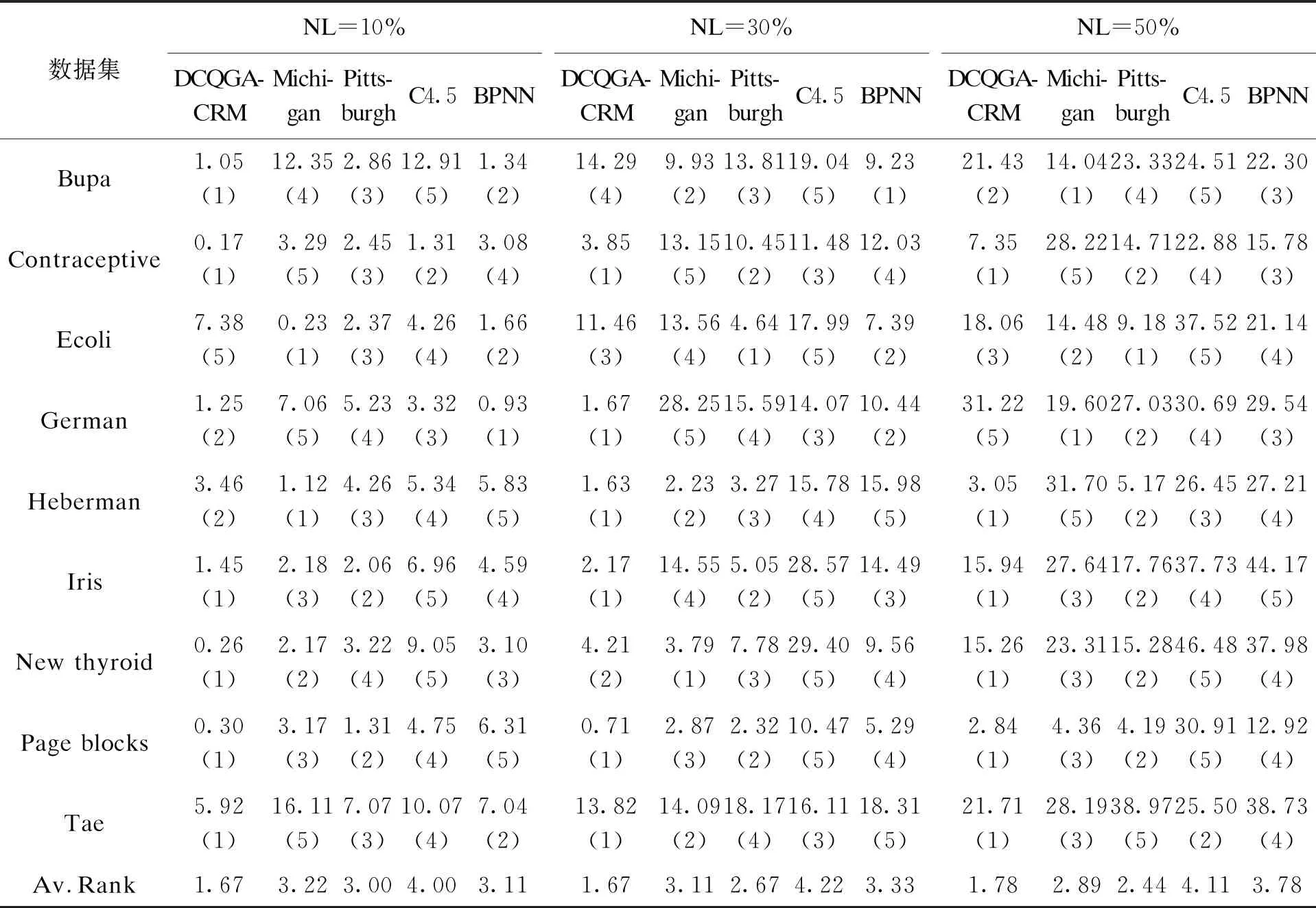
表5 不同噪聲水平下DCQGA-CRM與其他算法的RLA對比Tab.5 Comparison of RLA between DCQGA-CRM and other algorithms under different noise levels