獨塔斜拉橋基于流體粘滯阻尼器的減震分析

方曄飛，晏 竣，賀 峰

（1、長沙理工大學土木工程學院 長沙410114；2、中鐵五局集團第二工程有限責任公司 湖南衡陽421002）

獨塔斜拉橋因為其美觀、經(jīng)濟以及跨度大等特點，近年來越來越受到橋梁界的重視，并在全國各地迅速發(fā)展起來。雖然獨塔斜拉橋的數(shù)量在不斷增加，跨度在變大，但是由于其歷史較短，經(jīng)受地震等考驗也有限，相關震害資料不是很多，對其動力特性以及地震反應分析研究還不太全面也不完善。但是斜拉橋通常在交通運輸中占據(jù)著很重要的地位，并且投入的人力、財力巨大，對國家的經(jīng)濟有著非常重大的影響［1］。所以在斜拉橋結構設計中，必須進行嚴格的抗震分析，利用其地震響應規(guī)律，選出合理的方案。

1 工程概況

酉水三橋設計起點為K0+144.000，設計終點為K0+461.000，全長417 m。其中主橋設計成獨塔雙索面斜拉橋，斜拉橋全長359 m，其中主跨為196 m，邊跨為101 m+62 m=163 m ，邊跨只設有一個輔助墩。橋面寬度為29.5 m，主塔采用的是鉆石型塔，主梁采用的是預應力混凝土箱梁結構，主梁的截面形式為單箱三室截面，斜拉索進行扇形布置，采用的是雙索面，主塔每側設26對斜拉索，斜拉索在主梁上的基本索距為7 m，邊跨尾索區(qū)為4.5 m；塔上索距為2 m，全橋共104根斜拉索。鋼絲標準強度fpk=1 770 MPa。左邊三亭路方向的引橋為2×25 m 的預制小箱梁結構。其總體布置如圖1所示。

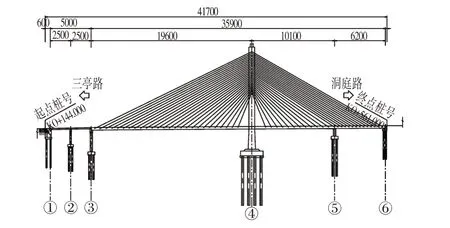
圖1 酉水三橋立面布置Fig.1 Elevation Layout of Youshui Third Bridge (cm)

主橋的主塔結構形狀為鉆石形，由下、中、上塔柱及下橫梁組成，總高127.586 m，分為下塔25.236 m、中塔59.84 m、上塔42.51 m，其混凝土標號為C50。橋梁主梁的橫斷面寬為29.5 m，具體布置為：1.5 m 索區(qū)+2.25 m人行道+10.5 m機動車道+1.0 m中央護欄+10.5 m機動車道+2.25 m 人行道+1.5 m 索區(qū)。其截面形式為單箱三室的混凝土箱梁，混凝土標號為C55；主梁梁高3 m。

2 有限元模型建立

主梁采用脊梁模式，這種模式的主梁的剛度系統(tǒng)和質量系統(tǒng)是正確無誤的［2］。斜拉索不考慮其垂度效應，所以采用桁架單元。主塔采用三維梁單元來進行模擬。主塔底部直接采用固結方式進行模擬。

本文借助專業(yè)軟件MIDAS/CIVIL 進行建模分析，模型共建立了401 個節(jié)點，294 個單元，漂浮體系（模型a）與加阻尼器的漂浮體系（模型b）唯一的區(qū)別就是在主梁與主塔之間是否添加縱向阻尼器。具體建模模型如圖2所示。

圖2 獨塔斜拉橋漂浮體系有限元模型（模型a）Fig.2 Finite Element Model of Floating System of Single-tower Cable-stayed Bridge（Model A）

3 粘滯阻尼器參數(shù)選取

葉愛君等人［3］的研究得出粘滯阻尼器的阻尼力跟相對速度關系可以表示為：

式中：F為阻尼力；C為阻尼系數(shù)；V為阻尼器兩端間的相對運動速度；a為速度指數(shù)。

從式⑴可知，粘滯阻尼器的主要控制參數(shù)是阻尼系數(shù)C 和速度指數(shù)a，其中a在抗震角度一般取0.3～1.0 之間［4］。所以對這2 個參數(shù)的選取直接關乎到它對整個結構的減震性能。為了確定合理的粘滯阻尼器參數(shù)，對速度指數(shù)a分別取0.3、0.5、0.7、1.0，阻尼系數(shù)分別取3 000 kN·s/m、5 000 kN·s/m、8 000 kN·s/m、10 000 kN·s/m，然后在單一縱向地震荷載作用下，對主塔塔頂（1#）、主梁主跨梁端（2#）進行縱向位移分析對比，對主塔塔底（3#）進行彎矩My分析對比。

從圖3、圖4 可以看出，當阻尼系數(shù)不變時，速度指數(shù)越大，主梁主塔的縱向位移越大，主塔塔底的彎矩也基本呈增大趨勢；當速度指數(shù)不變時，阻尼系數(shù)越大，主梁主塔的縱向位移越小，主塔塔底的彎矩剛開始減小后面趨于平緩，并且有增大的趨勢，與趙子鵬［5］的結論一致。在本模型中，從圖3、圖4 中的曲線趨勢可以知道，當阻尼系數(shù)C值小于5 000 kN·s/m時，主梁主塔的位移曲線變化趨勢明顯增大，當C值大于5 000 kN·s/m 以后，曲線要緩和很多；隨著阻尼系數(shù)C值的增大，主塔塔底的彎矩剛開始是減小，但是當C值增大到6 000 kN·s/m 時，彎矩減小的幅度趨于平緩，再往后面進行增大C值時，就有開始往上增加的趨勢。所以本文中的阻尼系數(shù)C取6 000 kN·s/m，而其速度指數(shù)a，本文主要考慮控制位移，然后綜合考慮內力變化，所以本文速度指數(shù)a值取0.5。模型b 將粘滯阻尼器設置在主梁和主塔之間，縱向對稱布置2個。

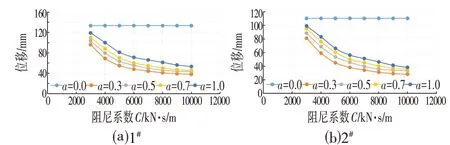
圖3 阻尼參數(shù)對縱向位移的影響Fig.3 Influence of Damping Parameters on the Longitudinal Displacement

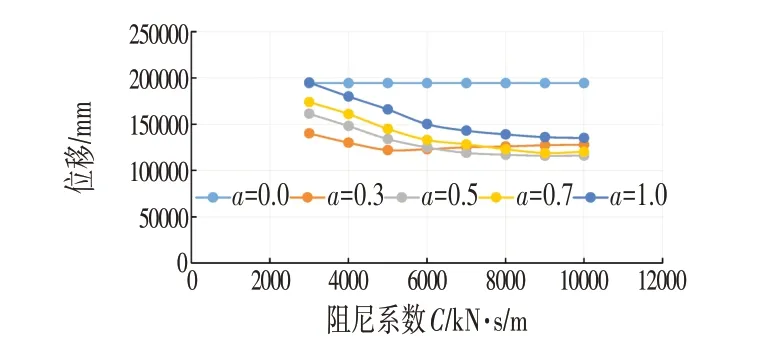
圖4 阻尼參數(shù)對3#彎矩My的影響Fig.4 Influence of Damping Parameters on 3# Bending Moment My

4 動力特性對比分析

程序中提供了3 種計算特征值的方法，本文采用子空間法。為了能夠使3個方向的振型參與質量達到90%以上，侯宇新等人［6］分析了150 階，因篇幅有限，本文只對前10階頻率和振型進行對比。

由表1 可知，加了阻尼器的模型b 的振型特征跟沒有加阻尼器的模型a 一樣，這表明添加粘滯阻尼器不會改變結構的振型特征。模型b 的頻率跟模型a 非常接近，只是模型b 的頻率比模型a 的頻率稍微小一點，這主要是因為模型b添加了縱向粘滯阻尼器，增加了阻尼，與范立礎［7］的結論一致。

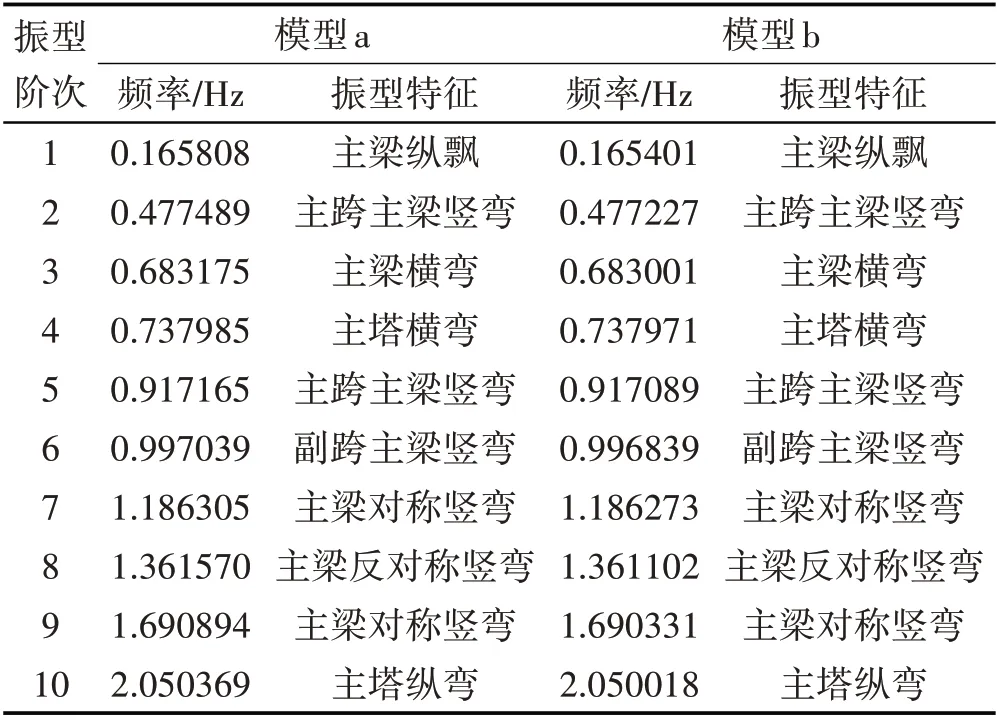
表1 2種模型前10階自振頻率統(tǒng)計Tab.1 Statistics of the First Ten Order Natural Vibration Frequencies of the Two Models

5 2種模型的時程分析對比

5.1 地震波的輸入

《公路橋梁抗震設計規(guī)范：JTG/T 2231-01-2020》規(guī)定對于沒有地震安全性評價報告的橋梁，可以參考已有的典型地震波根據(jù)實際情況進行調幅，或者人工合成地震波。在地震地面運動特征當中，對結構破壞有重要影響的主要因素有3個：頻譜特性、地震動強度和強震持續(xù)時間［8，9］。所以在本文中進行選取地震波時，根據(jù)這3個要素選取符合本橋場地情況的地震波，選取了1940 年的EI Centro Site，180 Deg，并對其進行調幅，具體如圖5所示。

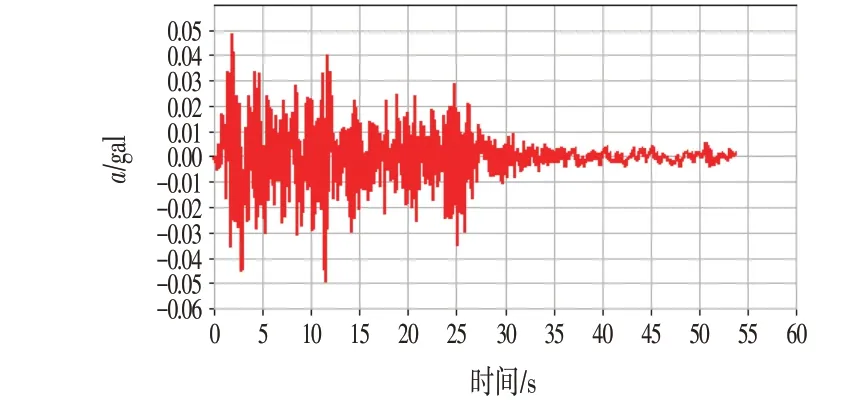
圖5 調整后的EI-Centro波Fig.5 Adjusted EI-Centro Wave

5.2 內力位移分析對比

在本文中，對2 個模型進行縱向和豎向2 個地震波方向輸入，對比在這個工況下2 個模型的主塔塔頂（1#）、主梁主跨梁端（2#）位移和2個模型主塔塔底（3#）的內力，具體結果對比分別如表2、表3所示。

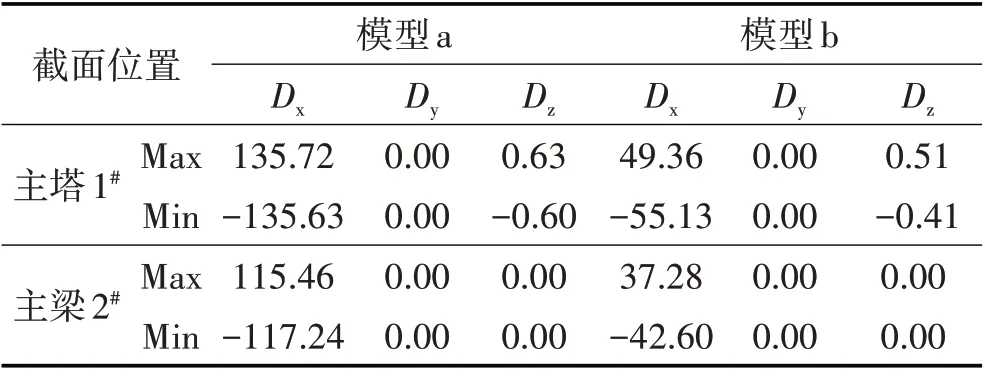
表2 地震荷載作用下2種模型的位移對比Tab.2 Displacement Comparison of The Two Models under Seismic Load（mm）

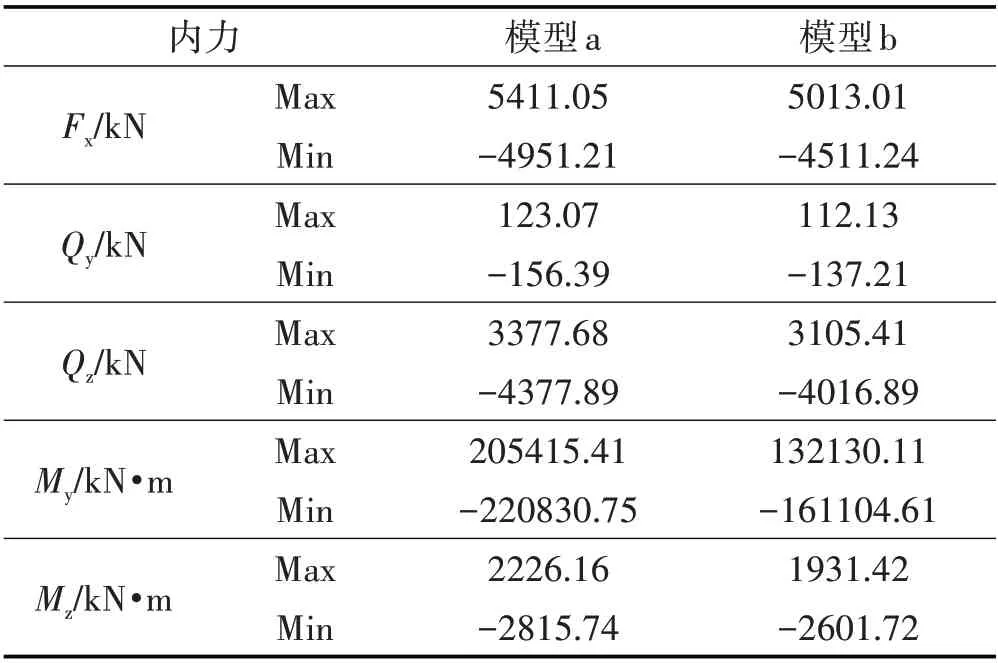
表3 地震荷載作用下2種模型3#截面的內力對比Tab.3 Comparison of the Internal Forces of Section 3 of the Two Models under Seismic Load

由表2、表3可知：

⑴對比表2 中的加阻尼器前和加阻尼器后結構的位移，可以看出縱向設置粘滯阻尼器可以起到明顯有效的抗震作用，其最大抗震率達68.08%。它之所以可以減小結構的位移，主要是因為阻尼器改變了橋面慣性力的傳播路徑，起到了良好的減震效果，與王雷［10］的研究結果一致。

⑵加粘滯阻尼器后，結構在地震荷載作用下，主塔的內力整體都有所減小，但是效果并沒有位移那么明顯。這是因為本文主要以結構位移為控制目標，所取的參數(shù)對于內力的影響沒有這么大。

6 結論

⑴通過對粘滯阻尼器的參數(shù)敏感性分析對比可知，不同的參數(shù)取值對結構的抗震效應影響非常大。所以在實際工程中，進行抗震設計時需要綜合考慮各種因素，確定合適的參數(shù)。

⑵加粘滯阻尼器后，結構頻率跟沒加之前的漂浮體系非常接近，只是稍微減小了一點，主要是因為粘滯阻尼器增加了結構的阻尼。

⑶通過添加粘滯阻尼器，既可以減小結構的位移又可以減小結構的內力，有效地起到抗震消能作用。