支護樁危險點的判定方法研究

何 欽，張記峰，丘北劉

（廣東省建設工程質量安全檢測總站有限公司 廣州510500）

0 引言

支護樁常見于基坑及邊坡支護、滑坡治理等工程，用于承載水平方向的土壓力或滑坡推力。在支護體系的設計有效期內，一般采用預埋測斜管的方式對支護樁進行水平位移監測。監測單位定期觀測并以變形允許值作為支護樁安全穩定性的判定標準，超限報警，向委托方反饋分析建議，為優化設計和指導施工提供依據，保障支護體系和周邊環境安全。

在進行支護樁水平位移監測數據分析時，通常認為樁體水平位移最大值處的應力狀態是最危險的［1-5］，即危險點。在監測數據超過變形允許值、樁體開裂漏水等異常情況下，采取搶險加固措施時通常基于這個結論展開。但結論并不能涵蓋所有情況，如2012 年12 月30 日發生的武漢市軌道交通3 號線王家灣站基坑垮塌事故［6］，項目設計開挖深度20.6 m，采用φ1 000@1 200 灌注樁圍護結構，樁長為31.6 m。開挖至17 m 左右時，支護樁在樁頂以下10 m 處折斷，引發冠梁破壞和基坑局部坍塌。而斷樁處水平位移監測值并非最大值。

因此，支護樁危險點的判斷方法應進一步完善，以便更準確地找到支護樁危險點。為此，本文以某項目中的支護樁水平位移監測數據為例，利用有限元分析方法對樁體的應力狀態進行了模擬，對樁體最大位移值并非最危險點的情況進行了分析。根據分析結果，本文提出了一種以樁段相對位移判斷最危險點的方法，并對該方法的適用性進行了分析和討論。結果表明，在樁身不存在明顯激凸點時，基于樁段相對位移的判別方法能有效找出樁體的最危險點。

1 基于測斜數據的樁體危險點數值分析

為彌補實際工程中樁體水平位移最大值處并非最危險點處而導致的判斷不準問題，本文首先利用測斜數據對樁體進行了有限元模擬分析，以找出樁體的最大應力點（危險點）。

1.1 方法介紹

本文建模所用測斜數據近似拋物線型樁，如圖1所示，測斜數據間距為0.5 m。由于實際工作中，測斜并非將樁體各處的水平位移均測出，而是按照固定間距測到某一深度為止［7］。因此在構建有限元模型時，其邊界條件應選為樁體底部僅限制縱向位移（重力方向）的單向約束，如圖1b 所示。該約束條件可考慮最后一個測點（最深處）水平位移對該點以上樁體的影響。同時，不限定該點轉動，即認為該點仍可因彎矩而產生轉角，使其與實際情況相符。

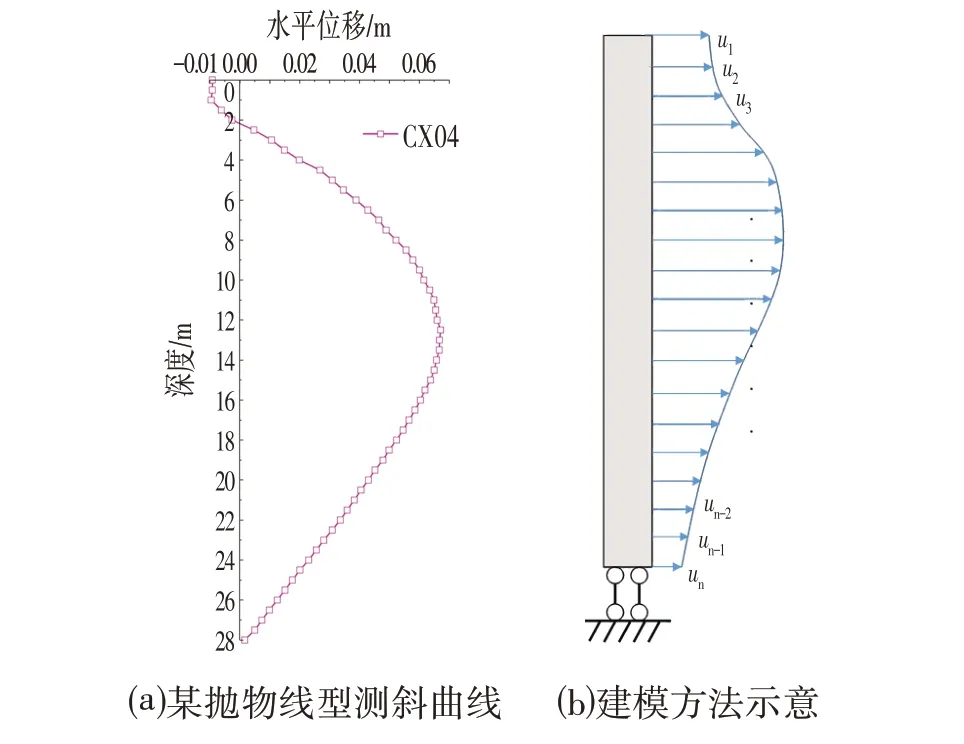
圖1 某拋物線型測斜及建模方法示意Fig.1 Schematic Diagram of a Parabolic Inclinometer and Modeling Method

模型邊界設置后，參考位移法［8］，將各深度的水平位移作為邊界約束條件作用在樁身各處，即以若干個集中荷載去逼近實際的外荷載條件，并限定其各點位移與實際相同。以此方法可以逼近樁體真實的受力情況，已知水平位移測點數越多則計算結果越接近實際。參考工程實例將支護樁截面取為直徑為1.2 m的圓形截面，單元類型為B22 梁單元，單元尺寸統一取為1 cm；其中，鋼筋混凝土的彈性模量E=31.5 GPa，泊松比ν=0.2。為使計算結果區分度更為明顯，本文選用的拋物線數據為一事故基坑的監測數據，此時樁體位移值已超過允許位移值。

1.2 模擬結果分析

模型計算得到全樁的主應力面最大主應力和最小主應力的分布曲線如圖2所示。

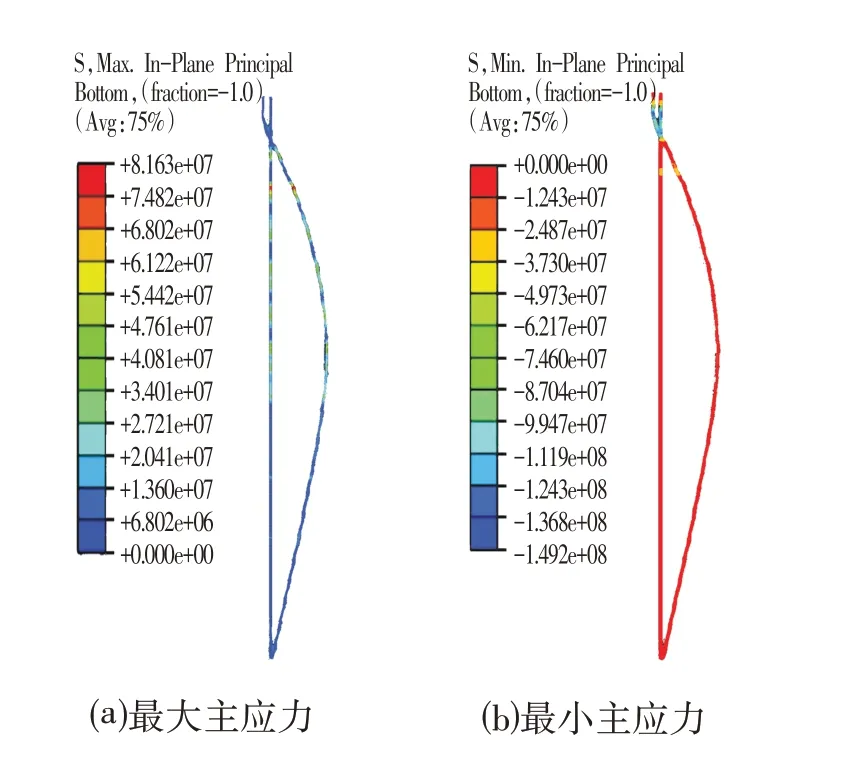
圖2 應力分布曲線Fig.2 Stress Distribution Curve

由于建模時樁單元局部坐標選擇以向上為正。因此，最大主應力對應著最大拉應力，而最小主應力對應著最大壓應力。經對比，樁體最大拉應力出現在4.53 m 深度處；最大壓應力處為1.06 m 深度附近。由于樁體最大水平位移位置分別為深度1.0 m（最大負水平位移）和12.5 m（最大正水平位移）處。因此，可以得出結論，樁體水平位移最大處并不一定是樁體應力狀態最危險處。上述結果說明，除采用規范規定的最大位移點對樁體危險點進行判別外，還需采用有限元分析等其他方法對其進行輔助判別。

2 判斷樁體危險點的樁段相對位移方法

在1.2 節分析中，本文通過數值分析再次說明了樁體最大水平位移值處不一定是最危險點的問題；說明實際工程中為確保樁體的及時二次支護，需要補充其他方法對樁體最不利應力位置進行分析。而利用樁體所有測斜數據對工程中所有樁體進行有限元建模分析，存在實際操作上的困難。為此，本文進一步提出了以樁段最大相對位移（相對位移法）對樁體最危險點進行判斷的方法，并對該方法的適用性利用有限元模擬分析進行了討論。

2.1 相對位移判別法

根據等距間隔的監測數據將樁體分割成多段小短樁，可以單獨研究其小段內的撓度變化。參考《建筑變形測量規范：JGJ 8-2016》［9］給出的撓度計算公式⑴（見圖3），將各小段兩端的水平位移監測數據視作梁段的整體位移進行扣除，則可以根據小段中點的水平位移計算出小梁段中點的相對撓度f1。

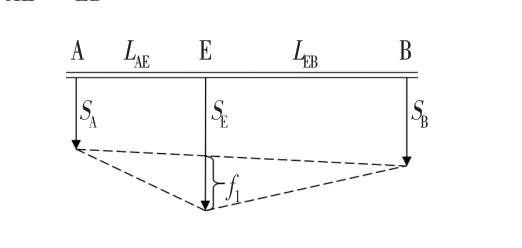
圖3 撓度計算方法Fig.3 Deflection Calculation Method

以圖1中拋物線型測斜曲線為例，經計算，該拋物線型變形樁體的各點換算的撓度（相對位移）按樁身方向繪制曲線如圖4所示。

圖4表明，樁體的最大正相對水平位移位于4～5 m深度間，而最大負相對水平位移則位于1 m深度附近；這一結果與1.1 節中有限元分析得到的最危險位置相符。說明相對位移法具有實用的可能性。

2.2 相對位移法適用性分析

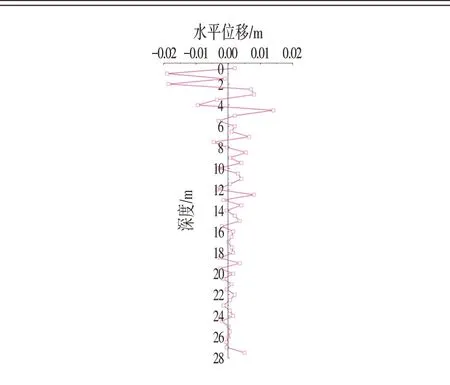
圖4 拋物線型測斜數據換算后樁相對位移曲線Fig.4 Pile Relative Displacement Curve after Conversion of Parabolic Inclinometer Data

2.1 節的換算結果說明相對位移法與利用所有測斜數據的有限元分析方法得到的危險點結果較為一致，但其對危險點的預測是否合理還需進一步的分析討論。為此，本文按照監測數據將樁體截成多段兩端固定梁體，將最大相對位移段取出單獨進行有限元模擬計算，并將其最大應力與全樁的有限元計算結果進行對比。然而，在實際案例中［10，11］，除連續光滑的拋物線型類測斜曲線外，還存在樁體變形出現突變點的激凸型測斜曲線（見圖5）。相對位移法對具有不同變形特征的樁體危險點的預測適用性可能存在明顯區別。為此，本文同時選用了2 組分布特點相差較大的連續光滑型（拋物線型）和曲線有較大凸變值的激凸型測斜曲線進行分析，以研究相對位移值作為樁體危險點分析方法的整體可行性。

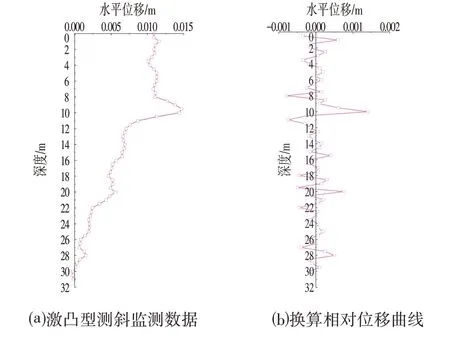
圖5 激凸型測斜監測數據和換算相對位移曲線Fig.5 Monitoring Data of Protruding Type Inclinometer and Conversion Relative Displacement Curve

2.2.1 建模方法

其具體建模思路如下：由于小梁段兩端的水平位移作為小梁段的整體位移扣除，因此小梁段應不存在水平和豎向位移，而僅存在由于彎曲而產生的轉動。因此建立模型時應約束小梁段的水平和豎向位移，而不約束轉動，如圖6a 所示。加載時，模型選為位移加載，在梁端中間施加計算得到的相對位移值。小梁段的梁單元局部坐標亦選擇向上為正反向，局部坐標選取如圖6b所示；梁單元截面尺寸和材料參數均設置與全樁計算相同。

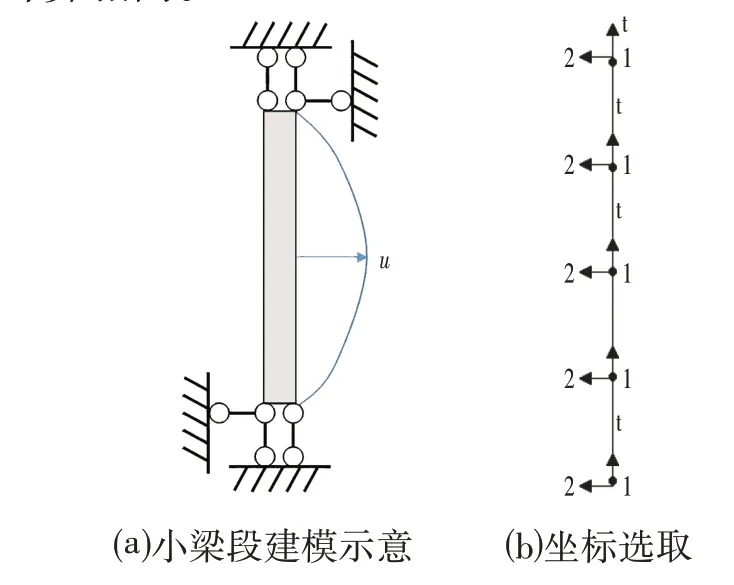
圖6 小梁段建模示意及其坐標選取Fig.6 Modeling of Trabecular Segment and its Coordinate Selection

模型計算所用加載位移值分別采用拋物線型（見圖4）以及激凸型測斜數據（見圖5）的最大和最小（負值）相對位移值。其中，圖5b 中的相對位移曲線是利用圖5a 中數據根據式⑴換算所得。因圖中有較明顯的位移突變點而命名為激凸型測斜曲線（見圖5a）。該激凸數據來自一處于安全狀態的基坑。

2.2.2 模擬計算結果與分析

經計算，拋物線型測斜數據換算得到的最危險梁段的最大正相對水平位移和最小水平位移計算結果分別如圖7所示。

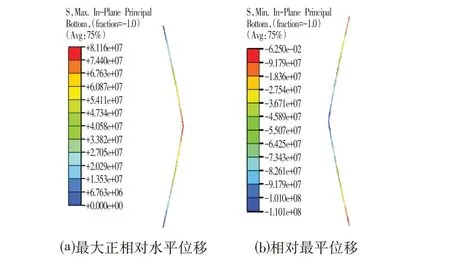
圖7 拋物線型變形樁樁身最大正相對水平位移和最小水平位移計算結果Fig.7 The Maximum Positive Relative Horizontal Displacement of the Parabolic Deformed Pile Minimum Horizontal Displacement Calculation Result

圖7 表明，最大正相對位移段的最大拉應力為8.116×107Pa，而全樁計算的對應結果為8.163×107Pa；最大負相對位移段最大壓應力為1.101×108Pa，而全樁計算結果相近位置處應力大致為1.492×108Pa。說明小梁段簡化單元的計算結果十分接近樁體整體計算的結果。相對位移法替代有限元分析方法用于輔助判別拋物線型變形樁體的適用性較好。

與之相應，激凸型曲線的樁體有限元建模計算結果如圖8、圖9所示。

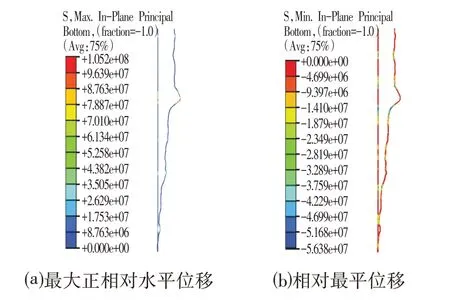
圖8 激凸型樁體全段應力分布情況Fig.8 Stress Distribution of the Whole Section of the Excited Convex Pile

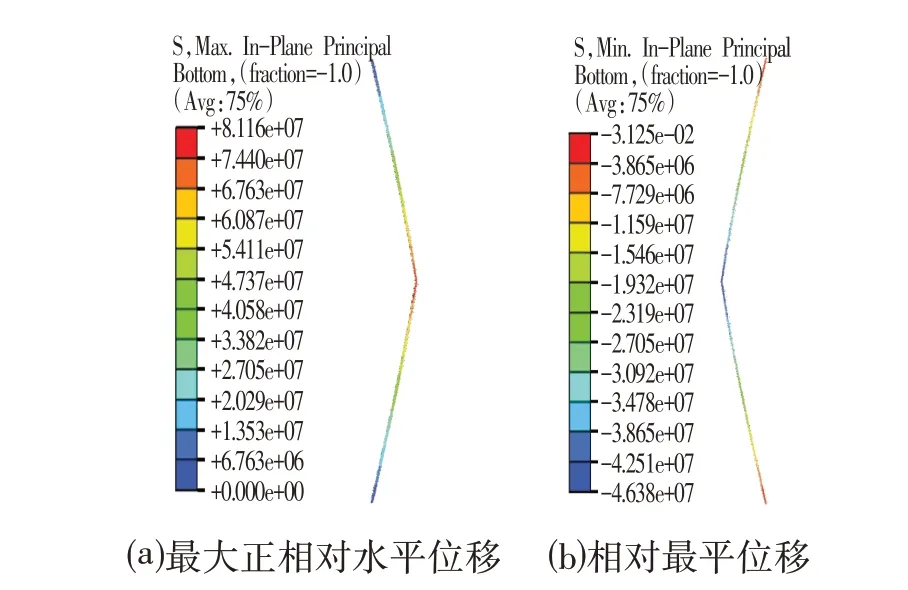
圖9 激凸型樁體小梁段應力分布情況Fig.9 Stress Distribution of Small Beam Section of Stimulated Convex Pile

根據圖8可知，全樁段分析時，激凸型變形樁體最大拉應力和最大壓應力位置分別位于深度9.902 43 m和10.051 90 m 處。而根據圖9 相對位移曲線找到的正負最大位移點分別為10.0 m 和8.0 m。說明存在激凸時，對應最大正相對位移點與整體計算結果的拉應力最大點較接近，但其最大負相對位移點僅對應整體計算結果的壓應力較危險點，而不是壓應力最危險點。因此，當曲線存在明顯的激凸點（曲線欠光滑，二階導數不為0）時，用相對位移判斷的方法可能會錯過最危險點。此外，從計算結果可以看出，處于安全狀態的激凸測斜曲線算出來的最大應力值已接近危險基坑（拋物線形）的計算結果，說明激凸形變形的樁體較平滑變形的樁體更為危險。

造成樁體激凸變形的可能原因有很多，一般是因為樁體本身或外荷載導致樁體受力情況不能保持平滑的過渡，例如樁身存在缺陷，樁后土體不均勻等情況。因此，利用短梁段相對位移分析的方法可能因為簡化條件不滿足而產生過大誤差；又或者因激凸變化的最大點沒有被監測點覆蓋而不能反應其最危險位置。不過，根據激凸型變形樁體全段有限元計算結果不難發現，激凸點一般為最危險受拉點；而激凸峰的突起兩端點一般為最危險受壓點。這一結論可以有效輔助判斷樁體的最不利受力位置。

3 結論

由于文獻［7］以樁體測斜水平位移絕對值作為判斷樁體危險點的主要判據，而實際工程事故表明存在例外，即樁體破壞點并非位移最大點的情況。為優化判斷方法，本文以某工程實測樁體測斜數據為例，通過有限元數值分析方法對其進行了探索和討論。本文先根據測斜數據作為位移量進行梁單元受彎情況分析，對樁體水平位移最大點并非應力最大點的問題進行了討論；之后給出了一種利用相對位移進行危險點判斷的方法，并利用截取小梁段進行有限元分析計算的方式對其適用性進行了討論。根據建模分析結果，本文得出如下主要結論：

⑴本文提出了一種較為簡便的樁體危險點判別方法——相對位移法，在樁體變形為連續光滑曲線時，該方法可得到與有限元位移分析較為接近的計算結果，以輔助判斷樁體的最不利受力位置。

⑵當樁體變形曲線出現明顯激凸點時，采用相對位移法不一定能準確地找出樁體最不利位置，存在錯過最危險點的可能性。

⑶激凸型變形樁體的激凸點一般為最危險受拉點；而激凸峰的突起兩端點一般為最危險受壓點。這一結論可以有效輔助判斷樁體的最不利受力位置。

本文所得結論均基于連續體有限元分析，將樁體視為均質彈性體，這在樁體出現較大塑性變形時可能并不適用。但本文給出的相關規律和判斷方法可為工程實踐提供參考。至于樁體的塑性變形狀態分析有待進一步的試驗和理論研究。