非線性動力吸振器式準零剛度隔振器的研究*

劉 楠，郭雅卓

(1.石家莊鐵道大學，省部共建交通工程結構力學行為與系統安全國家重點實驗室，河北 石家莊 050043;2.河北師范大學，化學與材料科學學院，河北 石家莊 050016)

0 引 言

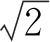
近年來，國內外學者也在不斷完善和發展準零剛度隔振器，并針對準零剛度的各種不足提出了多種辦法進行優化。彭獻[1]利用連桿機構設計制作了準零剛度隔振器的負剛度機構。徐道臨[2]利用五根螺旋彈簧設計了一種高頻低動隔振器。Wang Zhou[3]提出一種具有兩級準零剛度隔振系統，并建立了分段非線性動力學模型。Liu Yu[4]在隔振系統中加了輔助系統，降低傳遞率和跳躍現象。宋春芳[5]設計了一個隔振床用碟形彈簧與螺旋彈簧并聯實現負剛度機構。劉德穩[6]設計一種豎向準零剛度隔振器運用到建筑上，來防止地震波的影響。Han Liu[7]使用電磁非對稱磁齒結構設計了一種電磁隔振器。Liu Zhao[8]研究了庫侖摩擦對歐拉屈曲梁隔振器的影響。但是，經過多年發展，準零剛度隔振器存在較大共振峰的問題依然沒有得到有效解決。

筆者對準零剛度隔振器進行了創新，拉伸彈簧作為準零剛度隔振器的負剛度機構，設計了一種準零剛度隔振器，實現隔絕低頻的效果，但隔振系統存在較大共振峰。在此基礎上，設計了一個動力吸振器的準零剛度隔振器，即可有效減小幅頻響應曲線峰值，對低頻激勵進行有效隔絕，又可解決強共振峰問題。通過取長補短，使主系統不產生大的共振峰，在大部分激勵頻率下也能保持系統的穩定。

1 隔振器的靜力學分析

準零剛度隔振器由負剛度機構和正剛度機構組成，如圖1(a)和(b)所示。負剛度機構由拉伸彈簧4、活塞桿3和缸體2組成，在左側負剛度機構中拉伸彈簧4左端和活塞桿3連接，右側和缸體2連接。拉伸彈簧4在靜平衡位置處的拉伸量δ，剛度為kh。Fμ為負剛度系統中缸體2與活塞桿3發生相對運動時產生的庫侖摩擦力，l為負剛度機構單側的長度。正剛度系統由一個垂向彈簧6、立柱1和基座7構成，剛度為k1，阻尼為c1。質量塊5的質量為m1，在受到沿立柱1方向簡諧力F0cos(ωt)時，質量塊5位移用X1來表示。

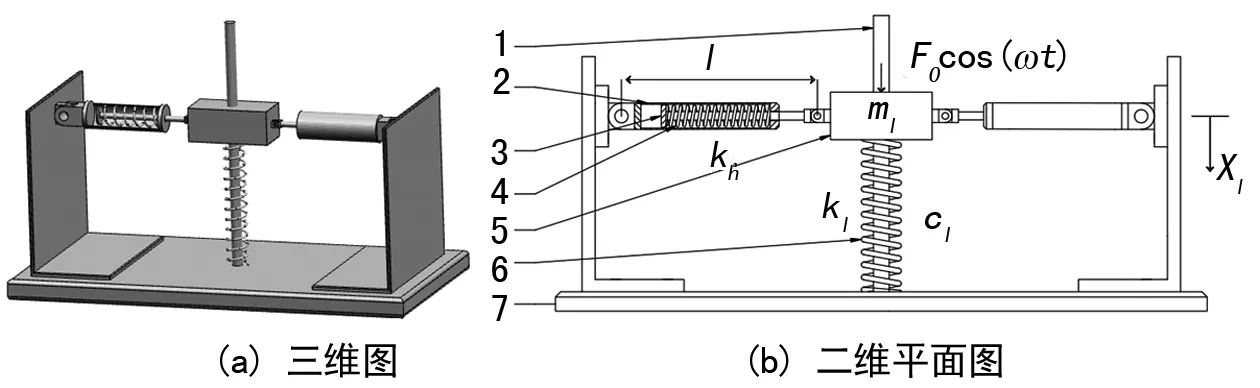
圖1 非線性準零剛度隔振器1.立柱 2.缸體 3.活塞桿 4.拉伸彈簧 5.質量塊 6.垂向彈簧 7.基座

在激振力作用下，m1質量塊進行位移X1，準零剛度隔振器的豎向恢復力為:

(1)

(2)

當式(2)除以x1時，可以得到隔振器的無量綱剛度:

(3)

令x1=0，代入式(3)確定隔振器準零剛度條件:

(4)

當滿足系統參數滿足式(4)時，隔振系統具有準零剛度。

由式(2)、(3)可得不同庫侖摩擦fμ、預緊力δ1和剛度比k下隔振器的恢復力-位移曲線，如圖2所示。在負剛度機構作用下，在只改變庫倫摩擦fμ，當庫倫摩擦fμ=0時，隔振系統在x1=0附近，出現系統剛度為零的情況，隨著庫侖摩擦fμ的增大，系統在靜平衡附近的正剛度特性不斷增強，零剛度特性消失。

圖2 在不同庫倫摩擦力條件下無量綱恢復力和無量綱剛度

從圖3中可以看出，在僅改變預拉伸長度δ1下，隔振系統的剛度也隨之發生改變，當預拉伸長度δ1=0.6時，在靜平衡位置x1=0附近，隔振系統出現剛度為零的情況，當負剛度機構中延長彈簧的預拉伸長度δ1不斷減小時，準零剛度隔振系統的正剛度特性呈增大趨勢。且從圖3中得到，系統剛度對預拉伸長度δ1的變化較敏感。

圖3 在不同預拉伸長度條件下無量綱恢復力和無量綱剛度

由圖4可知，只改變隔振系統剛度比k，系統的剛度特性發生改變，當系統剛度比k=0.7時，在靜平衡位置x1=0附近，隔振系統出現剛度為零的情況，而隨著剛度比k的增大，隔振系統正剛度特性越發明顯，零剛度特性消失。從各剛度-位移曲線可以得到，不同系統參數的變化對隔振系統零剛度特性的影響是不相同的，只有當系統參數滿足式(4)時，系統在靜平衡位置表現出準零剛度特性。

圖4 在不同剛度比條件下無量綱恢復力和無量綱剛度

使用泰勒展開[9]，將式(2)、(3)展開為:

(5)

(6)

由圖2～4所示，與式(5)、(6)可知，隔振系統無量綱力為奇函數，無量綱剛度為偶函數。

圖5給出了泰勒展開與原始表達式的比較。由式(5)和式(2)得到隔振系統的恢復力特性圖，如圖5(a)所示。由式(6)和式(3)得到的剛度特性如圖5(b)所示。圖中虛線為泰勒擬合式，實線為系統無量綱恢復力和無量綱剛度原式，從圖5可以看出，當位移x1較小時，泰勒展開的結果與原表達式一致，因此在小位移x1下，泰勒展開式(5)和(6)能夠近似表示隔振器的準零剛度特性。

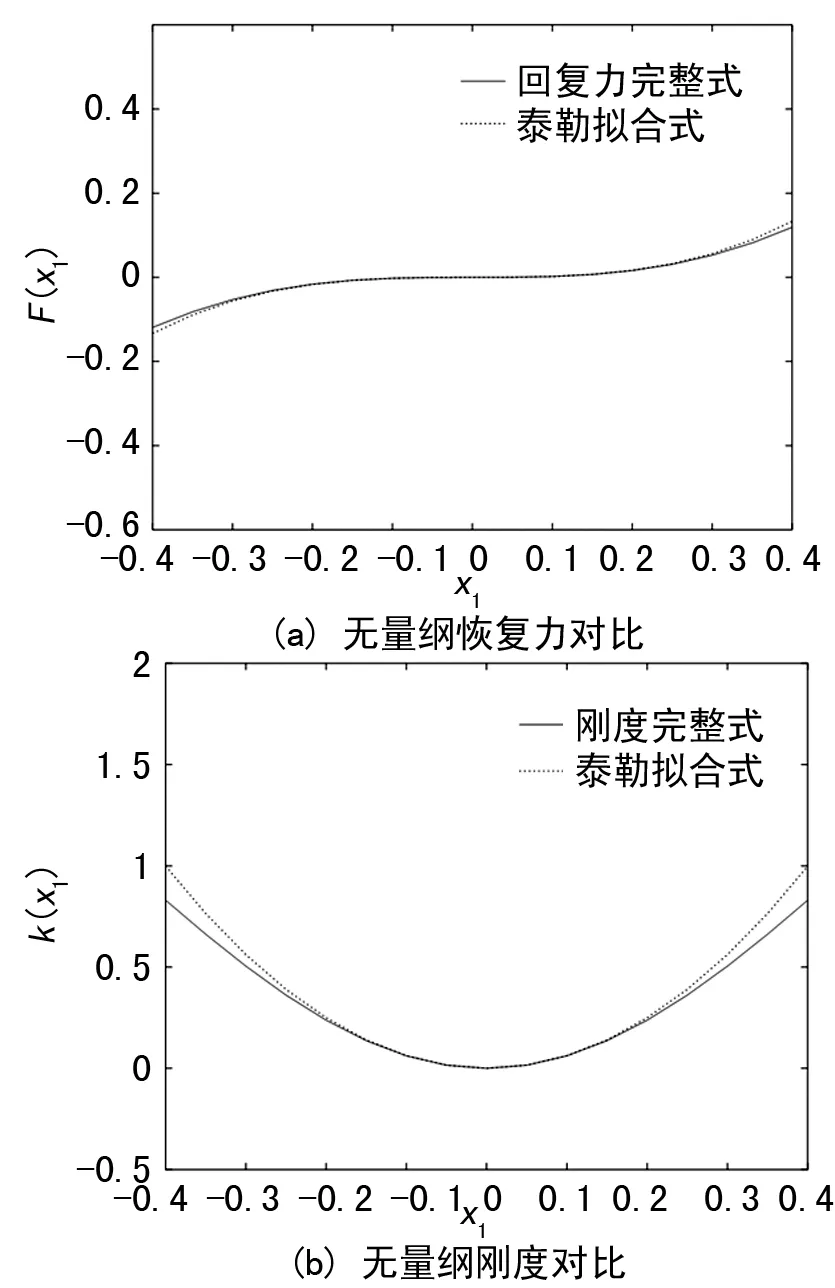
圖5 泰勒式的恢復力和剛度圖

2 可吸振式隔振器動力學分析

由于準零剛度隔振器受到大激勵力時，系統會產生強共振峰，針對這種情況設計一個動力吸振器來減弱隔振系統強共振峰問題，使系統在任何激勵頻率下都能保持穩定[10]。接地吸振器由吸振彈簧8和吸振質量塊9組成。由此設計了可吸振的準零剛度隔振器(VIDA)，如圖6所示，k2為吸振器彈簧剛度，c2為吸振器阻尼，k3為吸振器接地彈簧剛度，X1為主質量塊在簡諧力F0cos(ωt)激勵下的響應位移，X2為吸振質量塊的響應位移。

圖6 吸振式準零剛度隔振器 (8吸振彈簧、9吸振質量塊)

對可吸振式非線性準零剛度隔振系統中的質量塊施加一個簡諧力F0cos(ωt)作為激勵源得：

(7)

對各個參量進行無量綱化處理，令:

并代入式(7)得系統得運動微分方程為：

(8)

使用多尺度法[11,12]求解運動微分方程，且由于阻尼較小，激勵幅值小，非線性較弱，設ξ1=O(ε)，γ=O(ε)，vξ2=O(ε)，v2=O(ε)，Ω2=1+εσ，σ=O(1)，f0=O(ε)。

其中，ε為小參數，σ為調諧頻率，代入式(8)得:

(9)

研究準零剛度隔振系統一階近似解，需要兩個時

間尺度，令：

(10)

式中：τ0=τ，τ1=ετ，τ2=ε2τ。

定義偏導數算子來表示導數算子：

(11)

將式(10)和式(11)代入式(9)得：

(12)

(13)

(14)

設式(12)中第一個方程的解為：

(15)

其中cc為代表前面各項得共軛。

將式(15)代入式(13)可得：

(16)

在吸振隔振系統中，只考慮主頻的影響，因此可得式(16)第一式消除永年項的條件為：

(17)

而式(16)中第二式不存在永年項。

其中式(16)中特解x12和x22分別是：

(18)

將式(17)和(18)代入式(14)得：

(19)

其中：

根據式(19)中第一式消除永年項的條件為：

B1=0

(20)

式(19)中第二式不存在永年項。

設復函數A1(ετ,ε2τ)為：

(21)

將式(21)代入式(17)和(20)中，將實部和虛部分離得：

(22)

其中，幅值a和相位Φ為緩變時間尺度τ1的函數且為實函數。由式(22)得到幅頻響應方程為：

(23)

3 可吸振的隔振器線性分析

采用經典方法[13-14]，忽略可吸振的隔振系統的非線性項，建立動態方程。

(24)

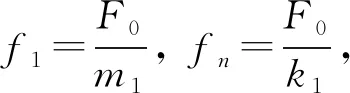
(25)

根據式(25)，得到了可吸振的隔振系統在線性條件下的幅頻響應公式：

(26)

其中：E1=2ξ2Ωv,E2=v2-Ω2

E3=2ξ1Ωv2-2ξ1Ω3-2ξ2μΩ3v-2ξ2Ω3v+2ξ2Ωv

E4=v2-Ω2-Ω2v2+Ω4-μΩ2v2-4ξ1ξ2Ω2v

4 帶減振器的隔振器參數分析

由式(23)得到準零剛度VIDA系統幅頻響應的非線性解析解，由式(26)得到線性解析解。在非線性解析方程中，m1=1 kg，m2=0.1 kg，δ=0.1 m，l=0.2 m，k1=1 000 N/m，kh=800 N/m，f0=0.07，fμ=0，v=0.58，ξ1=0.1，ξ2=0.2，而在線性解析方程中，v=0.85。主要分析系統參數的影響，包括固有頻率比v、隔振器阻尼比ξ1、地面吸收器的阻尼比ξ2、激勵幅值f0。

在該系統中，僅增加固有頻率比v就等于增加VIDA系統的剛度k2。如圖7(a)所示，橫軸為無量綱激勵頻率，縱軸為無量綱響應幅值。隨著固有頻率比v的增大，低頻共振段的響應幅值a1增大，高頻共振峰的響應幅值減小。由于固有頻率比v的增加意味著剛度k2的增加，地吸收器可以吸收更多的能量，低頻諧振峰值增大，說明峰值是由地吸收器引起的。由圖7(a)和(b)可以看出，隨著固有頻率比v的變化，線性和非線性解析解都存在此規律。

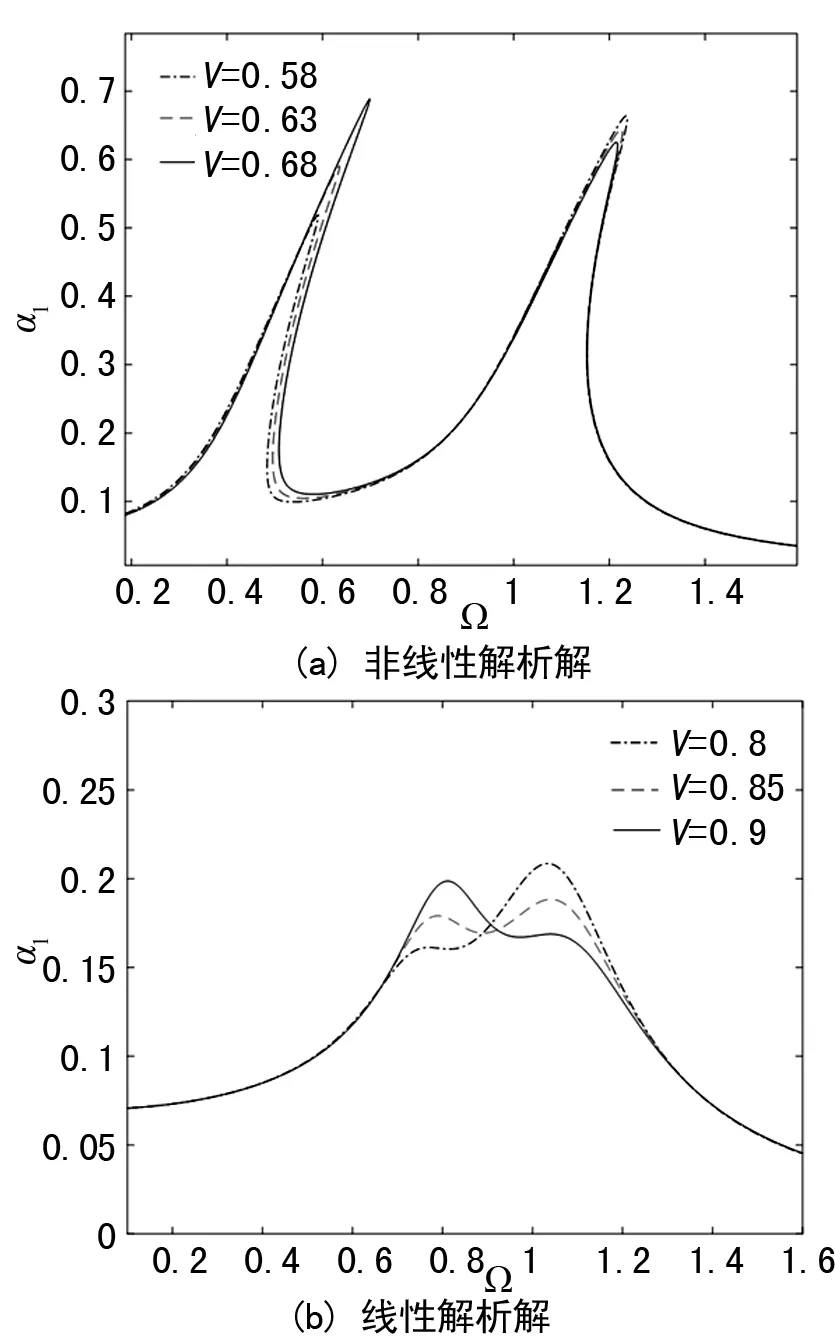
圖7 固有頻率比的影響

由于VIDA隔振系統存在阻尼，因此在幅頻響應圖中不存在反共振峰。如圖8(a)和(b)所示，橫軸與縱軸同樣為無量綱，隨著隔振器阻尼比ξ1的增大，響應幅值a1的兩個共振峰值明顯降低；且在圖8(b)中第二個峰下降比第一個共振峰，下降更為明顯。不同的是，在圖8(a)中，非線性也明顯減弱。

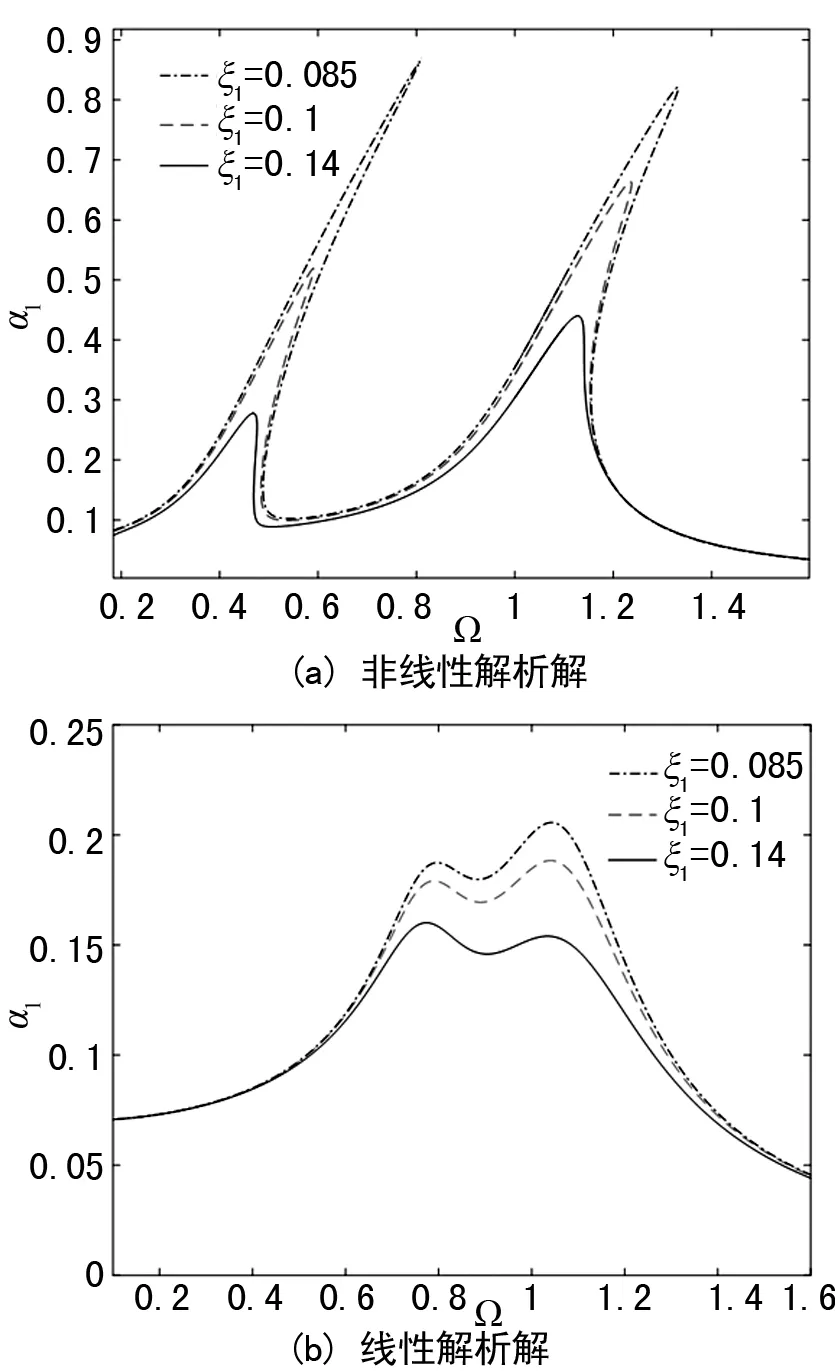
圖8 隔振器阻尼比的影響

如圖9(a)所示，當僅改變吸振器的阻尼比ξ2時，低頻共振處的響應幅值a1增大，而高頻共振處的響應幅值a1隨著阻尼比ξ2的增大而減小。同時，只有共振峰頻率段的幅值a1發生變化，而其他頻率段的幅值a1幾乎重合。這是非線性和線性解析解明顯的不同之處。如圖9(b)所示，隨著阻尼比ξ2的增大，兩個共振峰的響應振幅a1減小，而兩個共振峰之間的響應振幅a1增大。

圖9 減振器阻尼比的影響

如圖10所示，VIDA系統存在兩個非線性共振峰。當激勵幅值f0增大時，系統的非線性度增大，響應幅值a1相應增大，這是非線性系統特有的，也是線性減振系統最為明顯的區別。

圖10 激勵幅值的影響

5 對比與驗證

由于VIDA系統是非線性的，隔振系統具有阻尼，因此不能用固定值理論得到系統的最優參數。利用迭代算法和圖7～10中參數對幅頻響應的影響，得到最優參數為m1=1 kg，m2=0.1 kg，δ=0.1 m，l=0.2 m，k1=1 000 N/m，kh=800 N/m，f0=0.07，fμ=0，v=0.66，ξ1=0.1，ξ2=0.2。在此條件下，將VIDA系統與準零剛度隔振器進行了比較，并將非線性解析解與線性解析解進行了比較。

通過式(23)可得到非線性條件下接地吸振器與準零剛度隔振器幅頻響應曲線對比圖，如圖11(a)所示。VIDA系統的響應幅值峰值為a1=0.62，準零剛度隔振器的響應幅值峰值為a1=0.85，與沒有減振器的隔振器相比，響應幅值降低了27%。圖11(b)為最優參數下非線性幅值頻率響應曲線與線性幅值頻率響應曲線的比較，其中線性幅值頻率曲線由式(26)得到。線性響應的峰值為a1=0.25，比非線性峰值低60%。因此，在非線性二自由度模型的動力分析中，非線性項是不可忽略的。

圖11 最優參數下的比較圖

如圖12(a)所示，低頻共振峰的頻率比為在Ω=0.5處，如圖12(b)所示，高頻共振峰處的頻率比為在Ω=1.1處。數值解與解析解在兩個共振峰處的擬合度很高，證明了解析解分析結果的正確性。

圖12 數值解驗證

6 總 結

在對非線性準零剛度VIDA系統進行靜力學和動力學分析的基礎上，提出了一種新的VIDA系統，實現低頻隔振也避免強共振，并對系統參數進行了優化，并用數值驗證了解析解的正確性。

(1) 通過對非線性準零剛度隔振器靜力學分析，發現系統實現準零剛度與庫侖摩擦、預緊力和剛度比有關。只有當這三個系統參數滿足方程式(4)時，系統才能獲得準零剛度。

(2) 所提出的VIDA系統能夠有效地解決強共振問題，實現低頻隔振。在優化參數下，隔振器的響應幅值峰值比準零剛度隔振器降低了27%。

(3) 將VIDA系統的非線性解析解與線性解析解進行了比較。系統參數對兩個解的影響基本相同，但非線性項不可忽略，否則誤差可達60%。