基于長短期記憶神經網絡的冷水機組能耗預測

徐 麟 周傳輝 胡云鵬 李冠男 方 曦

基于長短期記憶神經網絡的冷水機組能耗預測

徐 麟1周傳輝1胡云鵬2李冠男1方 曦1

（1.武漢科技大學 武漢 430081；2.武漢商學院 武漢 430056）

空調系統中冷水機組是主要的耗能部件，節能潛力較大。由于空調系統的末端需求的變化性，準確開展冷水機組的能耗預測能有效的為機組的優化控制提供參考。因此，引入長短期記憶神經網絡（LSTM，Long Short-Term Memory）對冷水機組能耗進行預測，并結合EnergyPlus仿真模型數據和實際辦公建筑數據驗證LSTM能耗預測模型的預測效果。建立并優化LSTM冷水機組能耗預測模型。結果顯示，相比于反向傳播神經網絡和多元線性回歸模型，LSTM模型的計算時間有所增加，但LSTM模型的預測精度在三個模型中最高，LSTM能夠更準確的預測冷水機組的能耗。

冷水機組；能耗預測；長短期記憶神經網絡；時間序列

0 引言

隨著空調系統在建筑中的應用越來越廣泛，建筑能耗顯著增長。空調系統的運行能耗在建筑總運行能耗中占較大比例，約三成以上[1]。冷水機組作為空調系統的主要耗能部件，占空調系統總能耗的40%以上[2]，其節能潛力巨大。空調系統的能耗預測作為空調節能研究的重要部分，能為未來短期的系統能耗進行預測和評估，從而指導空調系統的優化管理以達到節能的目的[3]。隨著大數據時代的到來，多種基于數據挖掘的能耗預測方法被應用于能耗預測領域之中。由于數據挖掘方法可以在大量數據中發現隱含的信息，目前已成為比較流行的能耗預測方法[4-6]。

周峰等[7]運用支持向量機模型對辦公建筑的空調系統能耗進行預測，通過將預測值與實際值對比找到運行不合理的現象。任律[8]運用建筑監測系統數據，結合神經網絡模型實現了制冷機組的能效預測和自動診斷系統。嚴中俊等[9]運用某酒店的歷史數據進行訓練，建立了基于BP神經網絡的冷水機組能效預測模型并取得了良好的預測效果。但關于空調系統中冷水機組的能耗預測研究相對較少。

神經網絡預測法具有很強的非線性映射能力、很強的魯棒性以及強大的自學習能力，在能耗預測領域同樣得到了廣泛的應用。高揚等[10]基于前向神經網絡，精確的預測了建筑房間中的溫度和熱功率。Chang Yungchung[11]利用反向傳播神經網絡建立了水冷式冷水機組的能耗預測模型，通過冷凍水供回水溫度與冷卻水進水溫度預測機組的能耗。這些神經網絡模型都是非時序性的，即當前時刻的能耗值只與此時刻的輸入變量有關而與變量的歷史值無關。但是特定功能建筑物的使用計劃通常是固定的，時間信息往往反映了建筑的占用狀況和設備使用狀況[12,13]。數據的時序性往往對建筑能耗和冷水機組能耗有一定影響。

為了發揮神經網絡在能耗預測領域的優勢，同時使預測模型能夠處理時序性的數據。本文引入長短期記憶神經網絡（LSTM，Long Short-Term Memory）能耗預測模型對冷水機組能耗進行預測。Hochreiter S等[14]在1997年提出的LSTM模型是循環神經網絡（Recurrent Neural Network, RNN）的一種特殊形式，LSTM可以學習前面時間的信息并用于當前時刻的輸出。由于梯度消失問題的存在，RNN只對短期信息比較敏感。與RNN相比，LSTM增加了一個單元狀態負責承載長期狀態信息，彌補RNN對長期信息不敏感的缺點，使得LSTM能夠自動學習過去一段時間內的數據信息。篩選無用信息，保留有用信息，用來進行這一時刻的預測，使得預測模型更加精準。

本文采用LSTM方法建立冷水機組能耗預測模型，并運用EnergyPlus仿真數據驗證模型的預測效果。建立好LSTM模型后，進行輸入變量的相關性分析。本文著重于LSTM預測模型的優化，即根據預測結果優選模型輸入變量組成、滯后數、網絡結構和訓練次數。并將LSTM模型與反向傳播神經網絡模型和多元線性回歸模型的預測結果對比。結果表明基于LSTM時間序列的冷水機組能耗預測模型具有較高的預測精度。

1 LSTM原理

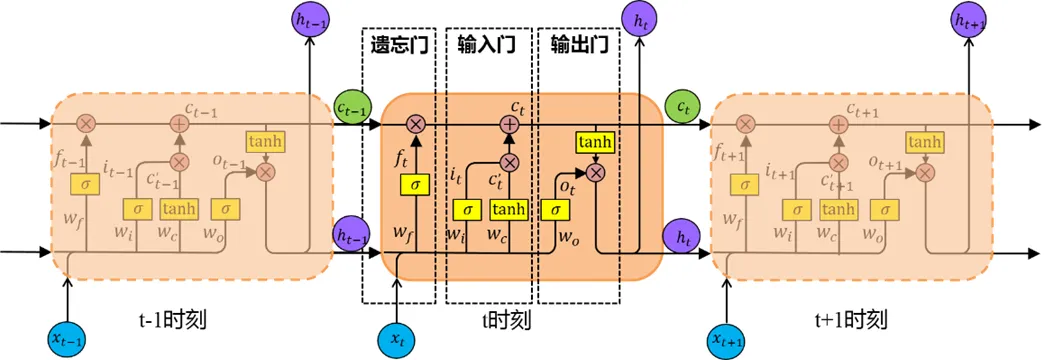
圖1 LSTM結構示意圖

三個門各自的作用和計算過程如下：

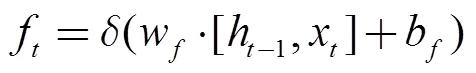
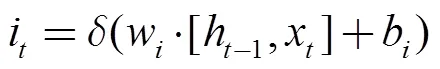
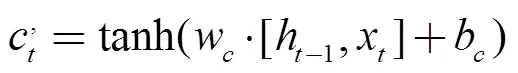
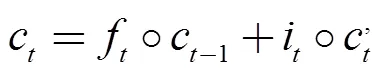
輸出門：決定當前模塊的輸出值。

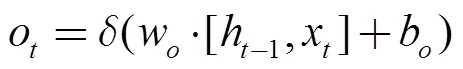
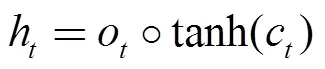
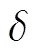
LSTM的訓練計算過程采用的是反向傳播算法類似的基于時間的反向傳播算法（Back Propagation Trough Time，BPTT）。LSTM的訓練過程主要分為四個步驟[15]：①按照公式（1）～（6）進行前向計算過程，得出每一個模塊的輸出值；②分別在時間和網絡層級兩個傳播方向計算每一個模塊的誤差項；③根據誤差項計算各個權重的梯度；④運用梯度優化算法更新權值。訓練結束后，使得時間序列上的信息形成一個平衡的長短期依賴。能夠運用LSTM進行冷水機組能耗預測工作。

2 數據來源和預測結果評價

2.1 數據來源

本研究采用EnergyPlus軟件構建了武漢某辦公大樓的空調系統仿真模型。夏季工況下，采用冷水機組和冷卻塔組合的常規一次回風集中空調系統。該系統包括冷凍水循環系統、冷卻水循環系統、空氣處理系統。仿真輸出得到正常工況下夏季制冷的完整運行數據集，輸出的變量為：日期（d），時間（，h），室外干球溫度（，℃），室外相對濕度（，%），太陽輻射強度（，W/m2），冷水機組能耗（Q，GJ）。數據在6月2號～8月29號之間采集。每一小時記錄一組數據,共581組數據。

2.2 預測結果評價

預測結果精度評價指標采用：平均絕對誤差（Mean Absolute Error, MAE）用來表示預測值和真實值之間絕對誤差的平均值，均方根誤差（Root Mean Square Error, RMSE）來反映預測結果和真實值之間的偏差。MAE和RMSE的值越小，預測結果的精度越高。

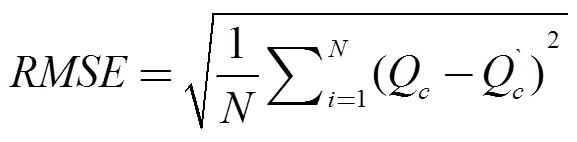
3 LSTM能耗預測模型的建立

3.1 數據處理

為去除不同變量的不同量綱和單位的影響，需要將數據進行標準化處理，以實現數據之間的可比性。采用z-score標準化方法，公式如下：

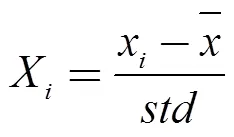
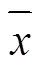
本文按照7:3的比例劃分訓練集和測試集，訓練集為前405組（45d），測試集為后176組（20d）。

3.2 輸入變量和滯后數

選取模型的輸入變量分為三類：時間信息、室外氣象參數和冷水機組能耗歷史值（Q）。為了使能耗預測模型獲得較好的預測效果，本文從三類變量中選取合適的變量組合來預測冷水機組的能耗。不同輸入變量的組合方式如表1所示。

表1 不同輸入變量組合

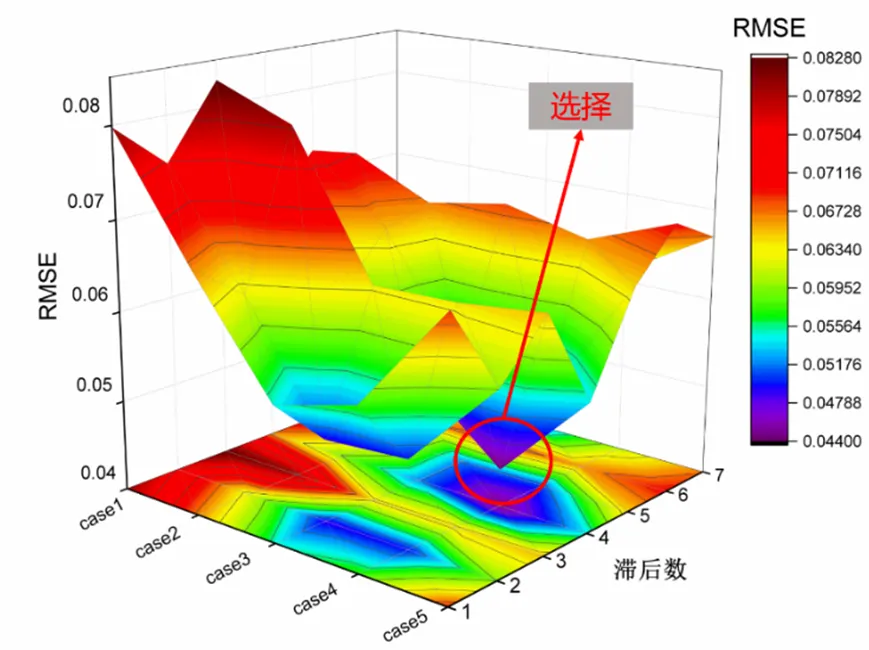
圖2 不同輸入變量組合和滯后數下預測結果

LSTM的滯后數是LSTM隱含層包含前后連接的同構模塊的個數，即時刻數在-到范圍內的時序數據參與了時刻的LSTM模型的建模。滯后數決定了當前時刻的LSTM單元中可以存儲多少歷史時刻的信息。滯后數的選取對LSTM模型的預測效果有著一定的影響。給定滯后數的取值范圍為1～7，結合不同輸入變量組合對能耗進行預測，尋找誤差最小的滯后數和輸入變量組合方式。如圖2所示，選取預測誤差最小時的輸入變量組合方式4：、、、、Q，滯后數為4建立LSTM預測模型。由圖2可知，輸入變量加入日期后，組合5較組合4的預測效果有所降低，說明本模型中冷水機組的逐時能耗與日期的相關性不大。

3.3 網絡結構

神經網絡的結構往往對神經網絡的性能有著較大的影響。一般來說，隱含層的層數越多，神經網絡預測的精度越高，但會使網絡結構更加復雜，增加計算時間。本模型選取隱含層層數的取值范圍為1-4。

隱含層的神經元個數的確定沒有明確的理論指導。一般以式（10）進行選取：

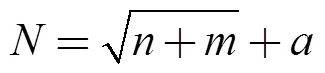
式中，為神經元個數；為輸入節點數；為輸出節點數；為取值范圍1-10的常數。

本文的輸入節點個數為5，輸出節點個數為1，根據式（10）計算出神經元個數的取值范圍為4-13。計算不同網絡結構（不同神經元個數、隱含層層數）下的預測精度，選取最優的網絡結構。得到的結果如圖3所示，選取隱含層層數為3，神經元個數13確定神經網絡結構。

圖3 不同神經元個數和隱含層層數下模型預測結果

3.4 訓練次數

訓練次數對LSTM的預測精度有著較大的影響。通過計算訓練次數對預測精度和計算時間的影響，綜合考慮以選取合適的訓練次數。

由圖4可知：隨著訓練次數的增加，模型計算的時間基本上呈線性增加的趨勢。RMSE隨著訓練次數的增大，先逐漸降低后趨于穩定，預測精度先逐漸增大后趨于穩定。當訓練次數超過150次時，模型精度雖有提高，但幾乎可以忽略，反而計算時間會有一定的增加。故選定訓練次數為150次。

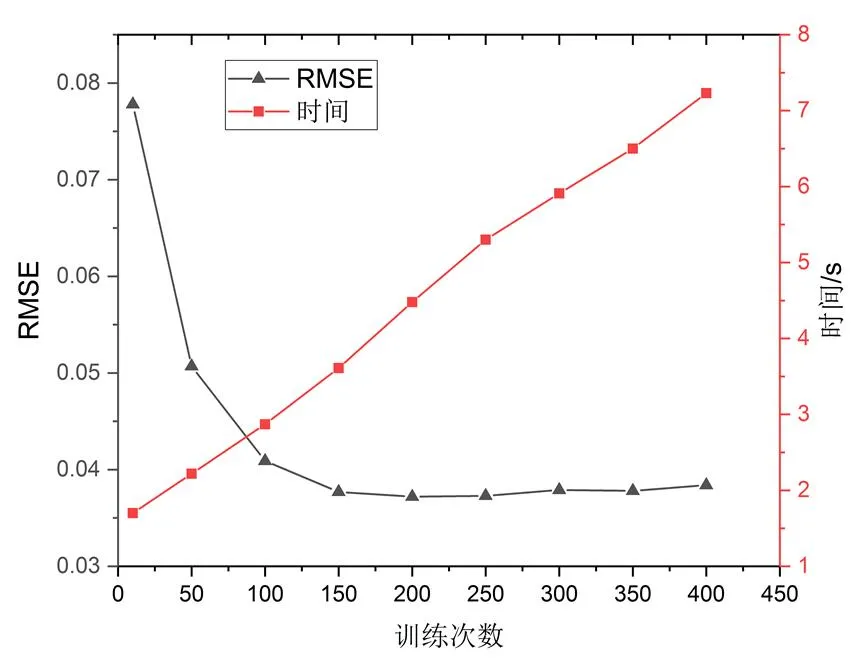
圖4 訓練次數對預測精度和和時間的影響

4 結果分析

綜上分析，根據LSTM的預測結果對模型的參數進行優選后確定LSTM能耗預測模型。本LSTM能耗預測模型的輸入變量為：時間（）、溫度（）、相對濕度（）、太陽輻射（）和冷水機組歷史能耗（Q），滯后數為4，神經網絡隱含層層數為3層，每層所含神經元個數為13，訓練次數為150次。實驗所用計算機配置如下：CPU:英特爾酷睿i7-6700k,4.0GHz；內存32GB。

為了驗證LSTM在冷水機組能耗預測中的優勢，在同一實驗環境中引入一種非線性的反向傳播神經網絡（BackPropagationNeural Networks,BPNN）模型和一種線性的多元線性回歸（Multiple Linear Regression, MLR）模型。BPNN是一種按誤差逆傳播算法訓練的多層前饋網絡，具有較強的非線性映射能力。訓練后的BPNN能夠學習和存貯輸入和輸出之間的映射關系，用于預測模型的建立。MLR可以研究一個因變量依賴多個自變量的變化關系，根據數據建立能耗預測回歸模型。選用相同的數據集建立BPNN和MLR能耗預測模型，對比分析LSTM、BPNN和MLR模型能耗預測的結果，如圖5所示。

圖5 三個模型對后20天逐時能耗值的預測結果

可以從圖5看出，三個模型的能耗預測值和真實值的變化趨勢基本相似，預測值和真實值總體上都比較接近，LSTM的預測值較BPNN和MLR更接近真實值。時刻63、72和81等是每一天上午冷水機組開機后所記錄的第一組數據，因為機組剛開機時，房間溫度較高，所需的制冷量較大，導致機組能耗較大，在圖中反映為出現峰值。此時，LSTM的預測值與真實值較為接近，而BPNN、MLR的預測值和真實值相差較大。說明當能耗突然增大時，LSTM的預測能力比BPNN、MLR強。

運用3.2節中提出的預測結果評價指標對3種能耗預測模型進行評價，結果如表2所示。

表2 兩種模型預測結果評價

為驗證LSTM在實際建筑中的冷水機組能耗預測的效果，引入Kaggle平臺上ASHRAE舉辦的建筑能耗預測大賽[16]所提供的實際建筑數據，從中選出五個實際建筑的運行數據集進行驗算（LSTM預測模型的建模過程與第三節所述相同），結果如表3所示。

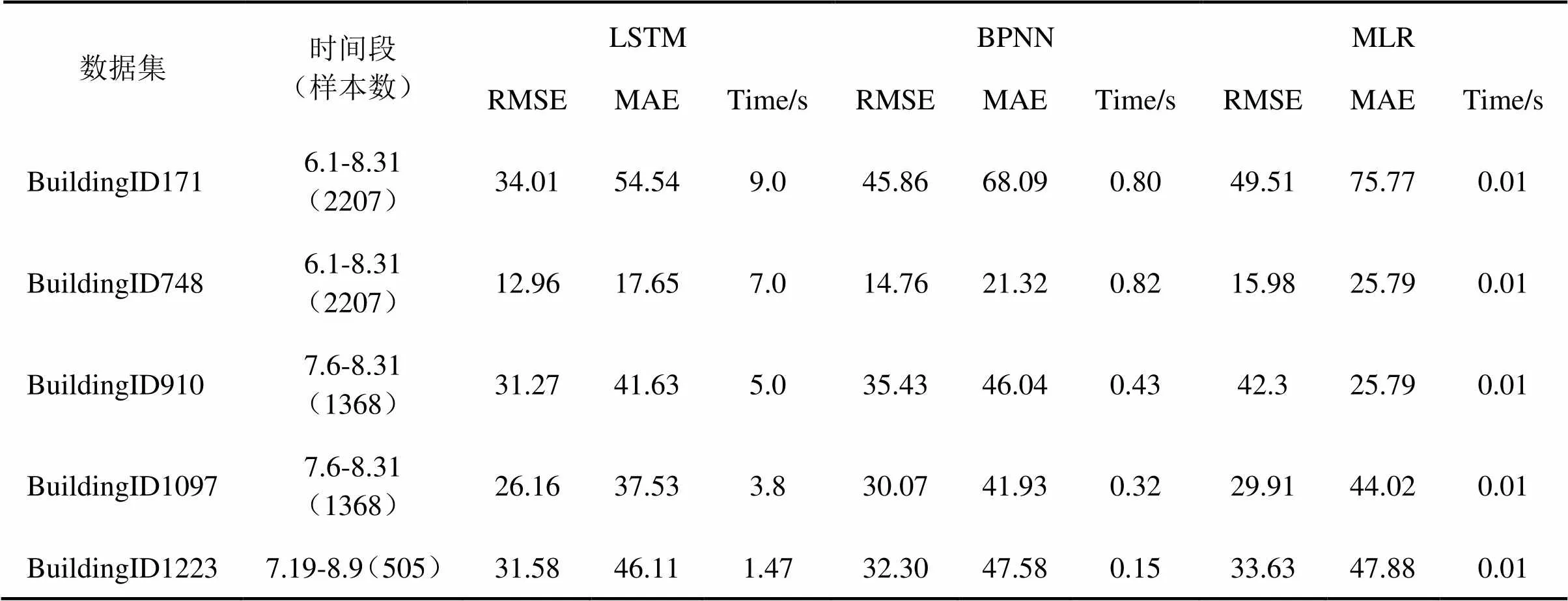
表3 實際建筑能耗預測結果

綜合來看，針對模擬和實際建筑冷水機組的能耗預測。LSTM模型的預測結果的RMSE和MAE的值是三種模型中最低的，預測精度較BPNN和MLR大大提高，LSTM能夠很好的預測冷水機組的能耗。LSTM模型的計算時間較BPNN、MLR有所增加，但如果計算過程在云平臺上進行，計算時間能極大縮短，LSTM較BPNN、MLR多出的計算時間可忽略不計。

5 結論

本文提出了基于LSTM的冷水機組能耗預測方法，優選輸入變量組成、滯后數、網絡結構和訓練次數后建立LSTM能耗預測模型。對模擬建筑和實際建筑中的冷水機組能耗進行預測，引入BPNN和MLR模型進行預測結果對比分析。得到以下結論：

（1）針對模擬建筑數據集，根據預測結果對LSTM能耗預測模型的參數進行優選得到：模型的輸入變量為：時間（）、溫度（）、相對濕度（）、太陽輻射（）和冷水機組歷史能耗（Q），滯后數為4，神經網絡隱含層層數為3層，每層所含神經元個數為13，訓練次數為150次。這種優化模型的方法也為后續的提高模型預測精度提供思路。

（2）針對模擬建筑和五個實際建筑的冷水機組運行能耗進行預測。LSTM模型的計算時間較BPNN、MLR有所增加，但LSTM模型的預測結果的RMSE和MAE的值是三種模型中最低的，預測精度較BPNN和MLR大大提高，LSTM能夠更準確的預測冷水機組的能耗。

（3）LSTM能耗預測模型相比于傳統的能耗預測模型，發揮了其能兼顧時序性和非線性問題的優勢，在冷水機組能耗預測中取得了更好的效果，有利于更好的支持空調系統節能工作。

致謝

感謝國家自然科學基金青年項目（51906181），湖北省高等學校優秀中青年科技創新團隊項目（T201829），湖北省教育廳科學研究計劃青年人才項目（Q20181110）資助。

[1] Fan C, Xiao F, Li Z, et al. Unsupervised data analytics in mining big building operational data for energy efficiency enhancement: A review[J]. Energy and Buildings, 2018,159:296-308.

[2] 胡云鵬,陳煥新,周誠,等.基于主元分析法的冷水機組傳感器故障檢測效率分析[J].化工學報,2012,63(S2): 85-88.

[3] 劉江巖,陳煥新,王江宇,等.基于數據挖掘算法的地鐵站內溫度時序預測方法[J].工程熱物理學報,2018, 39(6):1316-1321.

[4] 李紫微,林波榮,陳洪鐘.建筑方案能耗快速預測方法研究綜述[J].暖通空調,2018,48(5):1-8.

[5] Kadir Amasyali, Nora M. El-Gohary. A review of data-driven building energy consumption prediction studies[J]. Renewable and Sustainable Energy Reviews, 2018,81(1):1192-1205.

[6] 陳煥新,孫劭波,劉江巖,等.數據挖掘技術在制冷空調行業的應用[J].暖通空調,2016,46(3):20-26.

[7] 周峰,張立茂,秦文威.基于SVM的大型公共建筑能耗預測模型與異常診斷[J].土木工程與管理學報,2017, 34(6):80-86.

[8] 任律.基于大數據的制冷機房能效自動診斷[J].制冷與空調,2019,33(5):494-496.

[9] 嚴中俊,閆軍威.基于BP神經網絡的冷水機組能效預測方法[J].制冷與空調,2013,27(5):443-446.

[10] 高揚,陳坦,胡海濤.基于神經網絡的建筑節能預測方法[J].制冷與空調,2017,31(1):9-13,63.

[11] Chang Yungchung. Sequencing of chillers by estimating chiller power consumption using artificial neural networks[J]. Building and Environment, 2007,42(1): 180-188.

[12] Fan C, Xiao F, Zhao Y. A short-term building cooling load prediction method using deep learning algorithms[J]. Applied Energy, 2017,195:222-233.

[13] 杜前洲,姜梅,剛文杰,等.基于實測數據的夏熱冬暖地區校園建筑負荷分析[J].制冷與空調,2019,33(2):135- 142.

[14] Hochreiter S，Schmidhuber J. Long short-term memory[M]. Supervised sequence labelling with recurrent neural networks, Berlin, Heidelberg: Springer, 1997:1735-1780.

[15] 王鑫,吳際,劉超,等.基于LSTM循環神經網絡的故障時間序列預測[J].北京航空航天大學學報,2018,44(4): 772-784.

[16] ASHRAE-Great Energy Predictor Ⅲ. (2019-10-30) https://www.kaggle.com/c/ashrae-energy-prediction/overview.

Energy Consumption Prediction of Chiller Based on Long Short-Term Memory

Xu Lin1Zhou Chuanhui1Hu Yunpeng2Li Guannan1Fang Xi1

( 1.Wuhan University of science and technology, Wuhan, 430081; 2.Wuhan business school, Wuhan, 430056 )

The chiller is the main energy consuming part in the air conditioning system, which has great energy saving potential. Due to the change of terminal demand of air conditioning system, accurate prediction of energy consumption of water chiller can effectively provide reference for optimal control of the unit. Therefore, this paper introduces long short term memory (LSTM) to predict the energy consumption of water chillers, and validates the prediction effect of LSTM combined with the data of EnergyPlus simulation model and actual office building data. After the data is divided into training set and test set, the data is standardized. The energy consumption prediction model of LSTM chiller is established and optimized. The results show that compared with the back propagation neural network model and the multiple linear regression model, the calculation time of the LSTM model is increased, but the prediction accuracy of the LSTM model is the highest among the three models, and the LSTM can predict the energy consumption of the chiller more accurately.

Chiller; Energy consumption prediction; LSTM; Time series

1671-6612（2020）06-664-06

TU83

A

國家自然科學基金資助項目（編號：51906181）

徐 麟（1996.03-），男，在讀碩士研究生，E-mail：1085318635@qq.com

李冠男（1988-），男，講師，E-mail：leegna@163.com

2020-04-17