數學證明，在小學課堂真實發生

黃雅娓

課前思考：

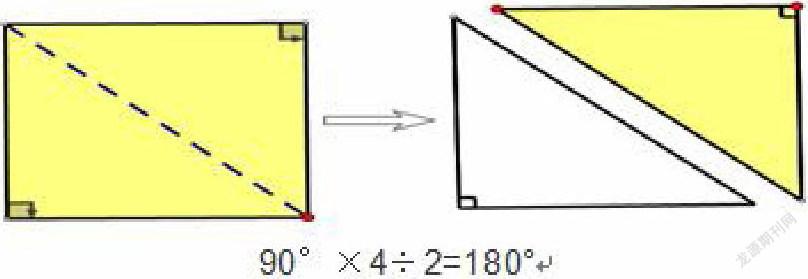
“三角形的內角和是 180°”，許多學生在課前都已經知道，但學生們只是停留 在“知道”這一層面。至于為什么內角和是180°，是怎么證明出來的，就不知其所以然了。而這節課采用的一般教學方法是先不外乎“量”、“拼”等實驗驗證，這屬于不完全歸納法，課上研究的個例有限。法國著名數學家帕斯卡所提出的證明方法，從演繹證明的角度來推導三角形內角和，是很好的完全歸納。帕斯卡是這樣證明的：長方形的四個角都是直角，四個角的和是360°;當長方形沿對角線一分為二后，就變成兩個直角三角形，每個直角三角形的內角和就是360°÷2=l80°;任何一個銳角三角形或鈍角三角形都可以沿高分為兩個直角三角形，兩個直角三角形的內角總和為180°+180°=360°，其中有兩個直角（這兩個不屬于三角形內角）拼在一起成了一條直線，所以銳角三角形一個內角的和是360°-90°×2=180°;帕斯卡的證明過程中利用到了內角的變化，所以內角的概念是非常關鍵的。那么這節課能否拋開傳統的“量、拼”等不完全歸納的方法，從數學演繹證明的角度“分割——轉化——求證”，上成一節完全歸納的數學證明課呢？。

學習活動：

活動一：內角，變，變，變

師：這是一個三角形。誰來介紹一下你認識的三角形？

引出內角：剛才你們說的三角形有三個角，這三個角就是三角形的內角。這節課我們就重點來研究內角的變化。

師：觀察談論：看看，角1，角2，角3發生了什么變化。（用幾何畫板拉動三個內角）

師：觀察四次變化的結果，你發現了什么？

生1：三角形的三個內角在拉動中，有內角變大，就會內角變小。

生2：無論怎么變，三個角的內角和是不變的，都是180°。

活動二：探究直角三角形內角和

師：三角形內角和是180°，你是怎么知道的？

學生起點：（1）書上看到或聽說?（2）量出來?（3）三個內角拼成平角

（方法2和方法3不是這節要研究的主要方法，不作為主講方法。）

（4）長（正）方形四個角都是直角，就是4個90°，對半切一半就是180°。

師：所有直角三角形的內角和都可以用這樣的方法（4）來驗證么？怎么證明？

生：所有的長方形都可以沿著對角線分割成兩個完全一樣的直角三角形。

小結：剛才我們運用了轉化思想，把長方形分割成兩個直角三角形，從而求證出直角三角形的內角和，看來“轉化——求證”這是數學學習的一個好方法。

活動三：練習與拓展

練習一：基礎練習，你能求出三角形第三個角么？（略）

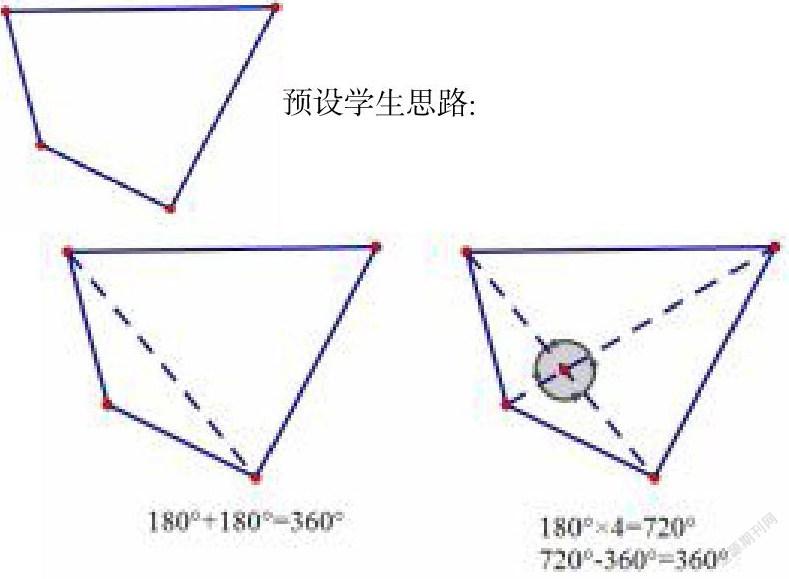
練習二：你能算出四邊形的內角和么？把你的想法畫一畫，算一算。

練習三：如果給你五邊形、六邊形，你打算怎樣求它們的內角和？用這樣的證明方法你還能求什么圖形的內角和呢？

預設學生思路：

總結：課前還有同學提出三角形內角和可以用度量角或者把三個內角拼成一個平角的方法，感興趣的同學可以回家試試，看看不一樣的思路又是怎么研究三角形的內角和的！

課后反思

本堂課的教學設計，很明顯有兩個“變”和一個“不變”。

一、變：從“實驗證明”到“數學證明”

本課最突出變化是課堂上沒有用傳統研究方法“量”和“拼”，“ 量”容易有誤差，“拼”破壞了原有三角形的完整性，這兩種方法都屬于實驗證明。而本課采用了法國著名的大數學家帕斯卡數學證明的方式來研究三角形內角和。有些老師可能為認為這種推理證明的方法太難，不大適合小學生，然而事實上學生們是有這方面的準備的，在長方形和直角三角形中已經積累了一定的嚴格證明的活動經驗。針對本節課知識層面不難的情況下來經歷一場數學證明的頭腦風暴，感受數學的嚴密性與邏輯性，給學生更加嚴謹的數學素養熏陶，不外乎是一次很好地機會。而內角概念的建立成了本課的研究起點。在三角形的角拉動的過程中，感知一個內角變大（小），另兩個內角就會變小（大）。但是無論怎么變，三角形的內角和是不變的。整個證明過程，我們從特殊三角形（直角）入手，這是最接近學生知識本源的地方，慢慢扶著，一步一步，學生在經歷數學證明的過程中，感受數學本身真正的魅力，并為后續的普通三角形的證明打下基礎。

二、變：從“不完全歸納”到“完全歸納”

“量”“拼”等實驗驗證的方法都是對個例進行研究，一堂課所能研究的個例畢竟有限，嚴格意義上來說，這時候得到的，還只是一種規律、一種猜想，還需要經過數學的嚴格證明，或者大量的實驗論證然后才能運用，這就是“不完全歸納”，而小學階段大部分的探索研究都屬于“不完全歸納”。而本課的教學設計，從特殊三角形（直角）入手，先研究了所有的長方形都能分割成兩個直角三角形，從而得出所有其內角和，緊接著運用本結論來求證銳角和鈍角三角形的內角和。所有的銳角或鈍角三角形都能分割成兩個直角三角形，得出這兩種三角形的內角和。又因為三角形按角分類屬于完全分類，從而得出所有的三角形的內角和，這就是一個完美的“完全歸納”的過程，開闊了學生的眼界，再一次體驗到數學求證的嚴謹美！

三、“不變”： “轉化——求證” 一路相隨

整個課堂，無論是教學直角三角形內角和，還是獨立研究銳角、鈍角三角形，又或者是后面的放手拓展四邊形形內角和，更或者是五邊形、六邊形……我們可以感受的是里面所蘊含的最本質的數學思考方法是不變的，那就是“轉化——求證”，這條暗線一直貫穿整堂課。數學證明過程是有思維含量的，但是學生們是有“法”可依，有章可循，并能發現用這一方法可以解決所有多邊形內角和。在這一過程中，學生的數學思維得到真正的一次歷練，空間觀念和轉化思想得到大幅提升。

完全歸納的數學證明課在小學課堂上是少之又少，因為這不僅需要教師的自身數學素養，也需要學生具有一定的數學求證思維和空間觀念，而這不是一蹴而就的，正需要我們珍惜每一次機會，為學生慢慢鋪好求證道路。