兩根“拐杖”(幾何法與坐標法)“走路”

◇ 山東 張林德

幾何法與坐標法是高中數(shù)學的重要方法,幾何法“寓數(shù)于形”,將數(shù)學問題轉(zhuǎn)化為幾何問題,使問題形象直觀,易于突破;坐標法“寓數(shù)于算”,將數(shù)學問題轉(zhuǎn)化為運算問題,降低思維難度,易于解答.本文通過例題分析幾何法與坐標法在平面向量、立體幾何、解析幾何中的作用,以期拓寬讀者的解題思路,提高解題能力.

1 平面向量中的兩根“拐杖”

例1如圖1所示,在面積為1的平行四邊形ABCD中,,則點P是直線AD上的動點,則的最小值為_______.

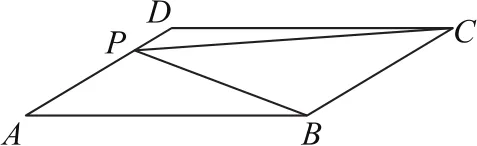
圖1

解析

如圖2所示,設AB＝m,BC＝n,因為該平行四邊形面積為1,則所以

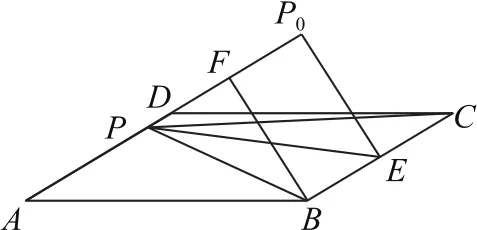
圖2

拐杖1:幾何法如圖2所示,取BC的中點E,連接EP,過E作EP0⊥AD,垂足P0,過B作BF⊥AD,垂足為F,因為AD∥BC,所以

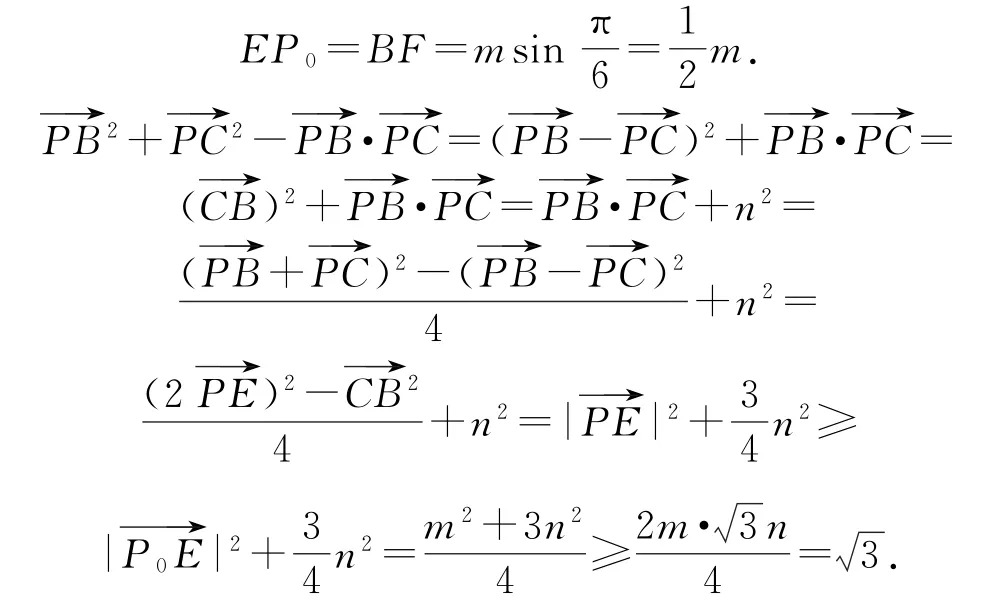
拐杖2:坐標法如圖3所示,以A為原點,AB所在直線為x軸,建立平面直角坐標系.

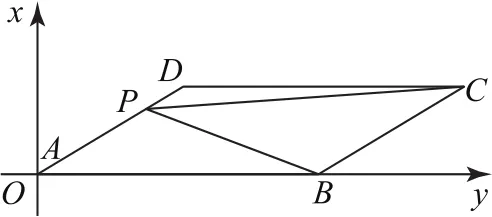
圖3

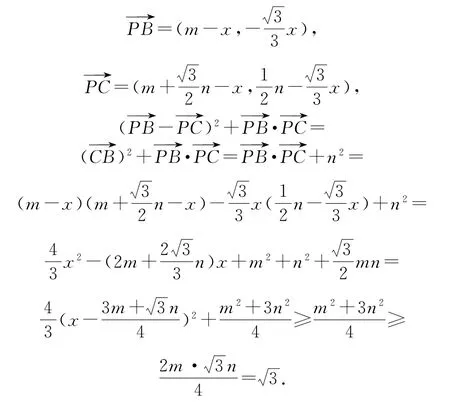
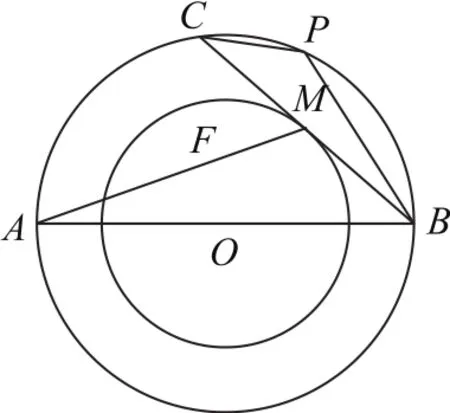
圖4

例2如圖4所示,兩個同心圓O的半徑分別為2和2,AB為大圓O的一條直徑,過點B作小圓O的切線交大圓于另一點C,切點為M,點P為劣弧上的任意一點(不包括B,C兩點),則的最大值是________.

解析

拐杖1:幾何法如圖5所示,作垂直于AM且與大圓O相切的直線,切點為D,該直線交AM的延長線于點E,過O作OF⊥AM,垂足為F,連接OD,PM,則OD⊥DE,OM⊥BM,M是BC的中點,四邊形ODEF是矩形,FE＝OD＝2.

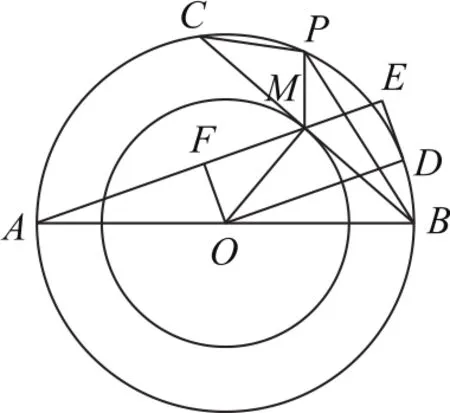
圖5

在Rt△OMB中,因為OM＝ 2,OB＝2,所以∠BOM＝45°,∠AOM＝135°.

在△OMA中,

拐杖2:坐標法以O為原點,OB所在直線為x軸,過點O且與OB垂直的直線為y軸,建立平面直角坐標系,則A(－2,0),M(1,1),P(2cosα,2sinα),,

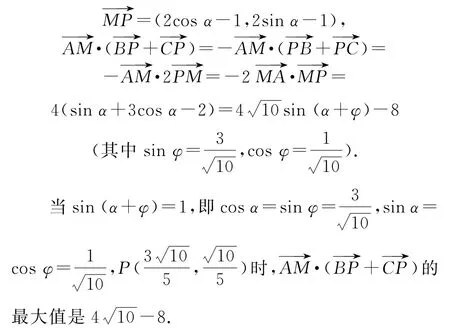
點評

通過以上兩個例題我們發(fā)現(xiàn),坐標法步驟更簡單一些,因此向量問題能用坐標法解決就盡量優(yōu)先使用坐標法.

2 立體幾何中的兩根“拐杖”

例3如圖6所示,在四面體ABCD中,△ABC是斜邊AB為2的等腰直角三角形,△ABD是以AD為斜邊的等腰直角三角形,已知CD＝,點P,Q分別在線段AB和CD上,則PQ 的最小值為_______.

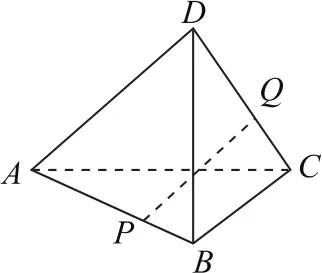
圖6

解析

拐杖1:幾何法

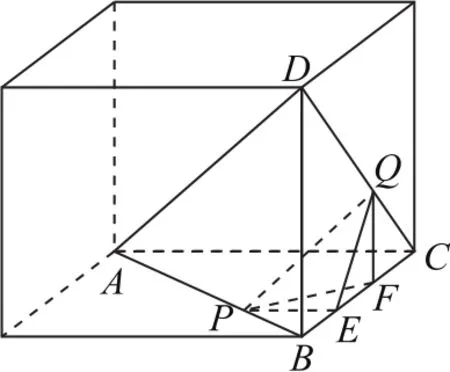
圖7

如圖7所示,為讓圖形直觀,把四面體放在長方體ABCD中.當PQ為線段AB,CD的公垂線時,PQ取得最小值.(兩條異面直線上兩點間距離的最小值為公垂線段的長度).過P作PE⊥BC于E,過Q作QF⊥BC于F,連接QE,PF,則PE⊥平面BCD,QF⊥平面ABC,由三垂線定理的逆定理知,EQ⊥CD,FP⊥AB.設BE＝x,則,由△EFQ∽△DBC,.

拐杖2:代數(shù)法如圖8,以B為原點,建立空間直角坐標系O-xyz,則所 以.

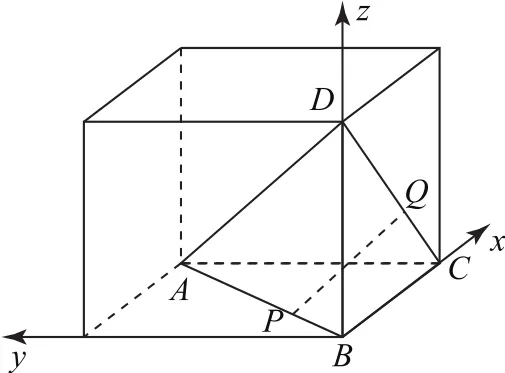
圖8

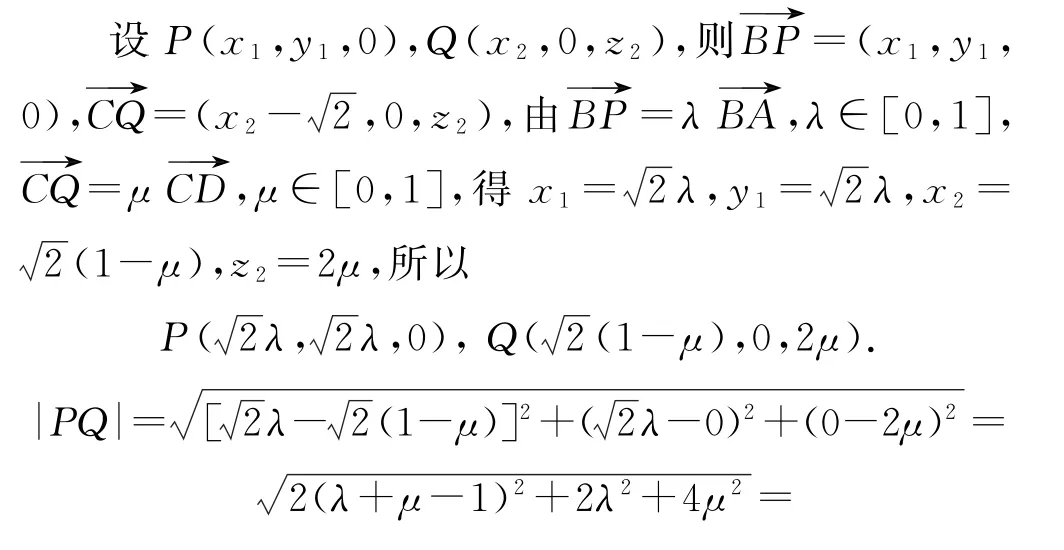
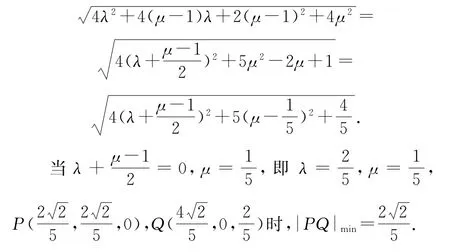
例4(2019年全國卷Ⅰ理18)如圖9所示,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1＝4,AB＝2,∠BAD＝60°,E,M,N 分別是BC,BB1,A1D的中點.

(1)證明:MN∥平面C1DE;

(2)求二面角A-MA1-N的正弦值.

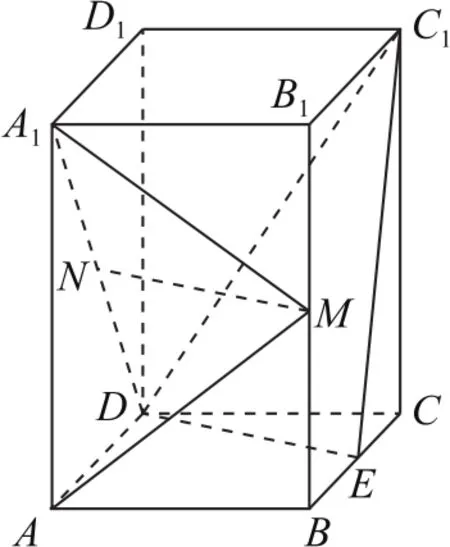
圖9

解析

(1)略.

(2)拐杖1:幾何法如圖10所示,取AB的中點G,連接DG,過G作A1M的垂線,垂足為H,連接DH,DM,因為四邊形ABCD是菱形,且 ∠BAD＝60°,所 以DG⊥AB,又因為ABCDA1B1C1D1是直四棱柱,所以平面ABB1A1⊥平面ABCD,從而DG⊥平面ABB1A1,DG⊥A1H,A1H⊥平面DGH,A1H⊥DH,所以∠DHG是二面角A-MA1-N的平面角.

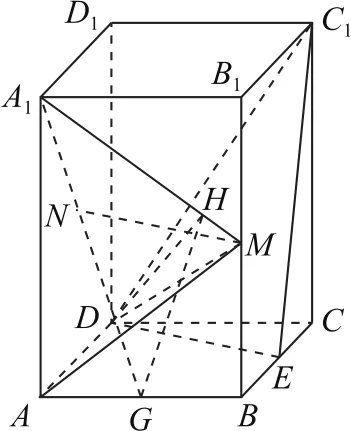
圖10

拐杖2:代數(shù)法如圖11所示,DE⊥BC,∠CDE＝30°,又∠ADC＝120°,∠ADE＝90°,以D為原點,DA,DE,DD1所在直線分別為x軸,y軸,z軸建立空間直角坐標系,,BE＝1,D(0,0,AB的中點為,所以平面AMA1法向量為.

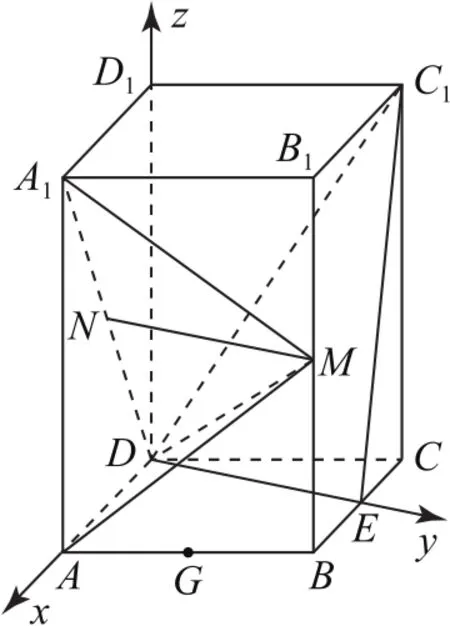
圖11

設平面MA1N的法向量為n2＝(x,y,z).由

令z＝1,得x＝－2,y＝0,所以平面MA1N的法向量為n2＝(－2,0,1).

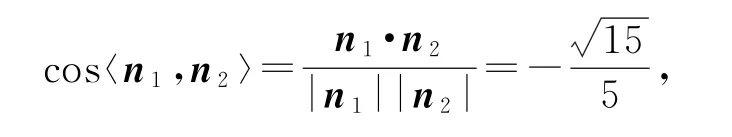
因為〈n1,n2〉∈[0,π],所以.

綜上,二面角A-MA1-N的正弦值為.

點評

立體幾何中的幾何法實質(zhì)上是將三維空間問題轉(zhuǎn)化為二維平面問題,坐標法實質(zhì)上是將立體幾何問題轉(zhuǎn)化為數(shù)的運算問題,二者體現(xiàn)的都是轉(zhuǎn)化思想.

3 解析幾何中的兩根“拐杖”

例5已知拋物線C:y2＝2px(p＞0)過點(1,－2),經(jīng)過焦點F的直線l與拋物線交于A,B兩點,A在x軸上方,Q(－1,0),若以QF為直徑的圓經(jīng)過點B,則|AF|－|BF|＝( ).

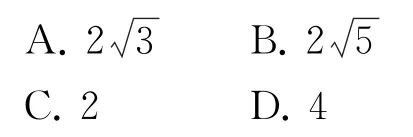
解析

拐杖1:幾何法1由已知可得p＝2,設AB的傾斜角為α,則|AF|＝2＋|AF|cosα,即同理.

又因為以QF為直徑的圓經(jīng)過點B,所以BQ⊥BF,在Rt△FBQ中,|BF|＝2cosα.所以2cosα,即1－cos2α＝cosα.

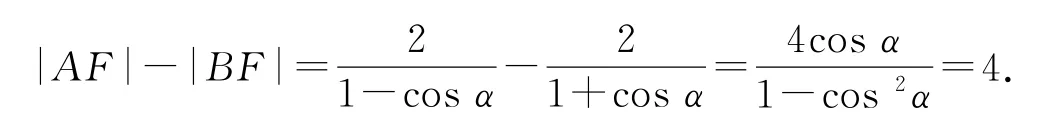
故選D.

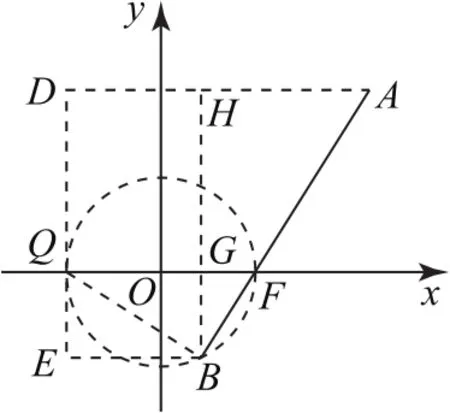
圖12

拐杖1:幾何法2已知拋物線C:y2＝2px(p＞0)過點(1,－2),所以4＝2p,拋物線C的方程為y2＝4x,F(1,0),Q在準線x＝－1上.如圖12,過A,B作準線的垂線,垂足分別為D,E,過B作AD的垂線,垂足為H,交x軸于G,連接BQ,因為以QF為直徑的圓經(jīng)過點B,所以BQ⊥BF.

設|OG|＝n,|AF|－|BF|＝m.|OQ|＝|OF|＝1,|BE|＝|DH|＝|BF|＝|QG|＝n＋1,|GF|＝1－n.在Rt△FBQ中,由射影定理得(1＋n)2＝2(1－n),即1－n2＝4n.

拐杖2:代數(shù)法由已知可得p＝2,F(1,0),設直線AB的方程為y＝k(x－1),A(x1,y1),B(x2,y2),聯(lián)立得k2x2－2(k2＋2)x＋k2＝0,x1x2＝1.

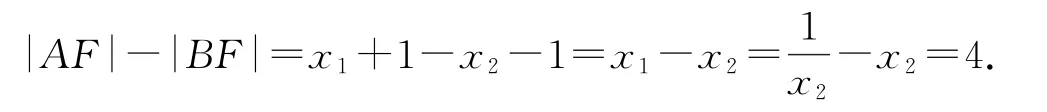
故選D.

例6如圖13所示,已知雙曲線b＞0)的左、右焦點分別為F1,F2,其右支上存在一點M,使得直線MF2平行于雙曲線的其中一條漸近線,則雙曲線C的離心率為( ).

解析

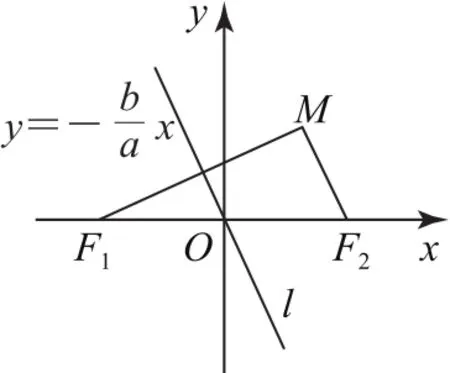
圖13

拐杖1:幾何法雙曲線C的漸近線方程為,設MF2平行于直線則,從而

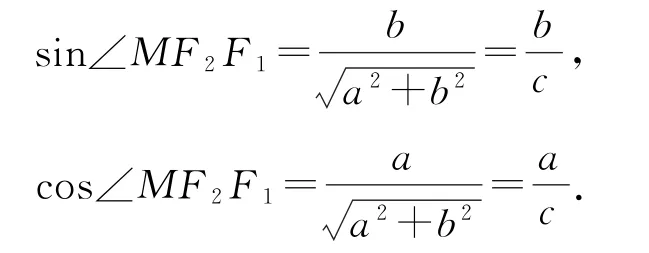
在Rt△F1MF2中,|F1F2|＝2c,所以

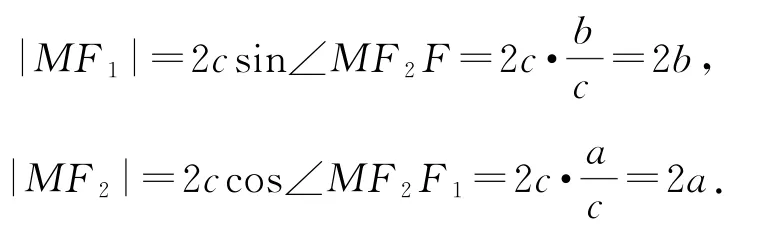
根據(jù)雙曲線定義,得|MF1|－|MF2|＝2a,所以2b－2a＝2a,即b＝2a,所以離心率為

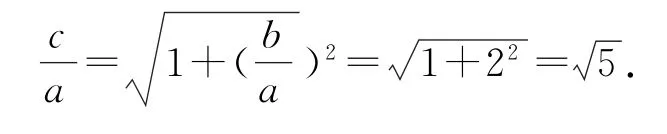
故選D.

拐杖2:代數(shù)法由得MF1⊥MF2,不妨設MF2平行于雙曲線C的漸近線l:y＝,所以MF1⊥l,l是線段MF1的中垂線,則直線MF1的方程為,設MF1與l的交點為N,聯(lián)立,解得x＝,又F1(－c,0),所以,由M在雙曲線上,得化簡得c2＝5a2,即離心率,故選D.

點評

解析幾何是聯(lián)系幾何與代數(shù)的一門學科,是用代數(shù)方法解決幾何問題的一門學科,解題的主要方法是坐標法,因為它具有幾何的性質(zhì),有時用幾何法可大大減少運算量,達到事半功倍的效果.

幾何法形象直觀,坐標法思路清晰,兩種方法各有千秋、相輔相成、優(yōu)勢互補,有些題目用幾何法簡單,有些題目用坐標法簡單,有些題目需要兩種方法結(jié)合,因此只有熟練掌握這兩種方法,才能游刃有余.