基于改進NSGA-Ⅱ的港機制造企業供應鏈網絡優化

李懷棟 胡堅堃 黃有方

摘要：針對港機制造企業供應鏈網絡面臨的經濟性、穩定性優化需求，本文以供應商、制造基地、港口和客戶在內的四級供應鏈網絡為研究對象，對網絡各級節點之間的穩定性和港口的物流能力進行評估，選取網絡的利潤、穩定性為優化目標建立多目標混合整數規劃模型。結合算例選擇矩陣實數編碼、行列交叉操作、差分變異算子對第二代非支配排序遺傳算法（non-dominated sorting genetic algorithm Ⅱ，NSGA-Ⅱ）進行改進。計算結果表明，該模型能夠對網絡的經濟性和穩定性進行有效優化，且算法能獲得Pareto最優解集，可為決策者提供較強的決策支持。

關鍵詞： 港機制造企業; 供應鏈網絡; 多目標優化; 第二代非支配排序遺傳算法（NSGA-Ⅱ）

中圖分類號： F552.6;F274 ? ?文獻標志碼： A

Abstract： In view of the economy and stability optimization needs of port machinery manufacturing enterprises’ supply chain networks， this paper takes the four-level supply chain network including suppliers， manufacturing bases， ports and customers as the research object， and estimates the stability between the nodes at all levels of the network and the port logistics capability. This paper selects the profit and stability of the network as the optimization objectives to establish a multi-objective mixed integer programming model. Combined with examples， the non-dominated sorting genetic algorithm Ⅱ （NSGA-Ⅱ） is improved by selecting the matrix real-number coding， the row and column crossing operation and the difference mutation operator. The calculation results show that， the economy and stability of the network can be optimized effectively by the model， and the Pareto optimal solution set can be obtained by the algorithm， which can provide decision-makers with strong decision support.

Key words： port machinery manufacturing enterprise; supply chain network; multi-objective optimization; non-dominated sorting genetic algorithm Ⅱ （NSGA-Ⅱ）

0 引 言

大型港機制造企業的供應商、制造基地、客戶遍布世界各地，在市場競爭越來越依賴于供應鏈競爭的當下，穩定的供應鏈有助于保持供應穩定、縮短生產周期、降低物流成本、促進快速交貨，并對提升港機制造企業的市場競爭力具有重要支持作用。近年來，國際經貿關系中不確定因素增多，企業在追求供應鏈網絡利潤最大化的同時，也在力求供應鏈網絡穩定性的提升。

目前，對供應鏈網絡優化的研究，主要與相關網絡特性相結合，但由于大型港機制造企業供應鏈網絡的自身特點，對其研究極少。LALMAZLOUMIAN等[1]指出制造企業供應鏈網絡中的不確定性主要體現在供應能力、制造能力和需求上，并指出風險主要存在于交付或運輸階段;KHALIFEHZADEH等[2]為提升整個供應鏈網絡的穩定性，將多級供應鏈網絡不同層級之間的穩定性之和作為優化目標;NEJAD等[3]對隨機中斷情況下能快速響應的供應鏈網絡展開研究，以供應鏈期望成本最小為目標，并考慮網絡的響應時間和擁堵情況;AZAD等[4]通過條件風險值法展開對供應鏈網絡的風險控制，以此對分銷和運輸網絡面臨隨機中斷的情況展開研究;李夢[5]在復雜網絡理論的基礎上，對物流、商流、決策流等“流”的時滯和企業之間的耦合強度與供應鏈系統的關系進行研究;張虹[6]對制造產能、運輸量及運輸方式等問題展開研究，并以最小化成本、最大化環境績效為供應鏈優化目標。

對算法進行改進的目的是提升算法性能，獲得問題最優解。在關于多目標問題求解的算法中：SHIM等[7]把遺傳算法中的目標分解與非支配排序組合，再進行進化梯度局部搜索;QIU等[8]引入自適應差分算法，并在算法收斂性、參數敏感性分析的基礎上，加入跨代變異機制;時思思等[9]提出一種基于動態擁擠度和自適應t分布交叉算子的第二代非支配排序遺傳算法（non-dominated sorting genetic algorithm Ⅱ，NSGA-Ⅱ），通過每次刪除擁擠度最低的解后更新非支配解的擁擠度，選出所需非支配解;路艷雪等[10]構建了多輸入多輸出的反向傳播神經網絡作為適應度函數的評價體系;吳暖等[11]引入雙向隨機變異算子，并嵌入非劣解的局部搜索，對NSGA-Ⅱ的性能進行提升。

本文在前人研究的基礎上，結合港機制造企業供應鏈網絡的實際情況，建立由供應商、制造基地、港口和客戶構成的四級供應鏈網絡，對網絡各級節點之間的穩定性和港口的物流能力進行評估，并以供應鏈網絡的利潤最大和穩定性最高為目標，建立多目標優化模型。結合算例對NSGA-Ⅱ進行改進，引入矩陣實數編碼、行列交叉操作、差分變異算子等，以期能夠提升港機制造企業供應鏈網絡的經濟性和穩定性。

1 問題描述

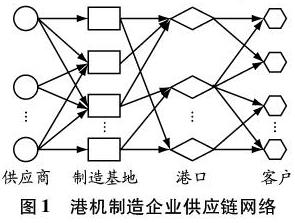
港機制造企業一般采用訂單生產模式[12]，其供應鏈網絡中包括多個供應商、多個制造基地和多個客戶。由于港機等大型裝備多采用海運，所以其供應鏈網絡中還應包括港口這一關鍵節點。為研究方便又不失一般性，本文結合港機制造企業實際情況，構建“供應商—制造基地—港口—客戶”4層供應鏈網絡，見圖1。在該網絡中，供應商向制造基地供給部件，制造基地具有制造、交付等功能，經過制造基地加工制造后最終將產品經由港口運輸交付給客戶。不同供應商供應的部件會存在價格差異，且各供應商與各制造基地之間關系的穩定性不同，通常供應價格較低的供應商由于市場廣闊，與制造基地之間關系的穩定性反而表現較為普通。對于港機制造企業而言，由于是面向訂單生產，其庫存量較低，為提升供應鏈網絡穩定性，通常會采用多元供應模式。在港機制造企業供應鏈網絡中除考慮供應商選擇、供需關系分配、成本控制外，結合實際運營情況，還應考慮影響供應能力的重要因素——港口物流能力[13]。因此，本文要解決的關鍵問題是：在滿足能力約束的條件下，以港機制造企業供應鏈網絡的利潤和穩定性為優化目標對供應鏈網絡進行優化。

2 模型建立

2.1 模型假設

①在整個供應鏈網絡中，相同功能的節點處于網絡的同一層級，分別代表供應商、制造基地、港口和客戶。產品從供應鏈上游向下游傳遞，不相鄰層級之間不存在跳躍的情況。②港機制造企業采用訂單生產模式。在制造基地中，產品一旦加工制造完成，就會被立刻運往港口送至客戶，因此制造基地無庫存。③每個制造基地的部件可以來自多個供應商，產品可運至多個港口;每個港口運輸的產品可以來自多個制造基地，并可以運往多個客戶;每個客戶所需的產品可從不同的港口運達。也就是說，在供應商至制造基地、制造基地至港口、港口至客戶的環節中，供需關系可以是多對多的情況。④各供應商、制造基地由于受生產能力的影響，產品的價格不同，加工的成本也不同，且各節點由于所處的位置不同運輸成本也不同。⑤各港口的物流能力不得超過該港口的能力限制，且供應商的供應能力、制造基地的制造能力和港口的物流能力是已知的。

2.2 符號定義

基本參數。S為供應商集合，s∈S;M為制造基地集合，m∈M;P為港口集合，p∈P;E為客戶集合，e∈E;T為時段集合，t∈T;qsjit表示供應商s在時段t對生產產品j所需的部件i的供應能力;rmjt表示制造基地m在時段t對產品j的加工制造能力;wpjt表示港口p在時段t對產品j的物流能力;dejt表示客戶e在時段t對產品j的需求量;θ表示投入產出系數;Γsmt表示在時段t供應商s與制造基地m之間供應關系的穩定性;Λmpt表示在時段t制造基地m與客戶p之間供應關系的穩定性;Θp表示港口p物流能力評分。

成本參數。bsit表示在時段t從供應商s處采購部件i的單位價格;vsmit表示部件i在時段t從供應商s運到制造基地m的單位運輸成本;gmjt表示在時段t在制造基地m加工制造產品j的單位成本;kmpjt表示產品j在時段t從制造基地m運到港口p的單位運輸成本;ypejt表示產品j在時段t從港口p運到客戶e的單位運輸成本;cejt表示在時段t客戶e采購產品j的采購價格。

決策變量。αmsit表示在時段t制造基地m從供應商s處采購的部件i的數量;βsmit表示部件i在時段t從供應商s運到制造基地m的數量;γmpjt表示產品j在時段t從制造基地m運到港口p的數量;λpejt表示產品j在時段t從港口p運到客戶e的數量;ωsmt為0-1變量，若在時段t供應商s為制造基地m供應部件，則ωsmt=1，否則ωsmt=0;σmpt為0-1變量，若在時段t將產品從制造基地m運往港口p，則σmpt=1，否則σmpt=0;ω～pet為0-1變量，若在時段t將產品從港口p運往客戶e，則ω～pet=1，否則ω～pet=0。

3 模型求解

在多目標優化問題中，通常各目標之間相互制約，即某些目標的優化會使其他目標的期望降低;對于同一個問題，由于決策者偏好不同，可能會做出不同的決策：因此，對于多目標優化問題，重在找到Pareto最優解集，從而提供更多決策支撐。NSGA-Ⅱ在多目標優化領域求解效果顯著，具有簡單、高效、適應性強且應用廣泛的優點，是其他算法所不能比擬的[14]。然而，NSGA-Ⅱ也存在容易陷入局部最優、計算效率不高、解集分布性較差等不足。結合本文雙目標優化模型，對NSGA-Ⅱ進行有針對性的改進，以期獲得Pareto最優解集。經典NSGA-Ⅱ流程見圖2。

NSGA-Ⅱ的關鍵在于基因編碼、適應度函數選擇、選擇操作、交叉操作和變異操作[15]。根據本文算例需求，采用矩陣實數編碼和行列交叉操作，并引入差分法將變異算子改進為差分變異算子，對算法進行改進。選擇操作采取錦標賽選擇法。為使算法與算例結合，以及提升算法的收斂性、穩定性和全局搜索能力，對算法進行設置，具體如下。

3.1 染色體編碼與解碼

基于供應鏈網絡的層級和供應關系的特性，選用矩陣實數編碼方法，并以矩陣作為染色體個體展開遺傳操作，以降低運算復雜度和保持個體基因的完整性。

編碼方式如下：種群規模為s′，第k代種群Pk={A1，A2，…，As′}，其中Ai表示第k代種群中的第i個個體，即矩陣染色體，Ai=（auv）n×m，auv表示基因元素，其中i∈{1，2，…，s′}，u∈{1，2，…，n}，v∈{1，2，…，m}。

矩陣Ai的大小取決于供應鏈網絡層級數和供應關系中最多的同級節點數，基因元素auv與供應鏈層級之間具有相關性，反映與上層供應者之間的關系。如矩陣Ai為一個4×5階矩陣，則表示有4層供應網絡，各級節點數最大值為5，其中a32=（100，0，0，0，200）表示第3層第2個節點接受第2層第1節點的100單位供貨量和第2層第5個節點的200單位供貨量，而0則表示節點之間零供應。

3.2 交叉操作

針對算法所采用的矩陣實數編碼，為有效進行個體間的交叉操作，進行行交叉操作和列交叉操作。

行交叉操作。對于采用n×m階矩陣編碼的個體Ai和Aj，隨機產生兩個由0、1構成的n維向量Bi和Bj，若Bi與Bj相乘后特征值為1，則交換相應的Ai與Aj的任意一行，若相乘后特征值為0則停止。以此類推，種群中任何兩個個體都將完成行交叉。對通過行交叉操作產生的子代都要檢驗其是否滿足約束條件（8）～（10），若不滿足，則進行剔除。對滿足約束條件的，采用局部錦標賽法，保留父代和子代個體中適應值較大的個體。

列交叉操作。列交叉操作類似于行交叉操作，對于種群中每兩個父代個體都隨機產生兩個由0、1構成的n維向量。區別在于，由于供應商、制造基地、港口和客戶數量的不同，列交叉操作后產生的子代個體可能會存在不滿足約束條件（3）～（5）的情況，對不滿足條件的進行剔除。對滿足約束條件的，采用局部錦標賽法，保留適應值較大的個體。

3.3 變異操作

針對NSGA-Ⅱ存在種群多樣性不足的問題，引入差分變異算子，取代NSGA-Ⅱ中原本的變異算子，以增強算法局部搜索能力。經過變異操作后，父代個體Ai更新為A*i=rAbest+（1-r）Ai式中：r為變異影響因子，反映了經迭代尋優后得到的最優個體Abest對變異方向的影響程度，其值越大則影響越大，通常r∈[0，1]。

差分變異算子搜索方法涉及距離閾值、相鄰個體的選擇等。距離閾值的確定方法是尋找種群非支配解集Ω在子目標Fi下的2個極值端點，求得目標值差，記為Δ，再根據公式求出子目標Fi的距離閾值D：D=2Δ/（Ω-1）D在進化過程中隨Ω規模的變化而變化，從而確保得到的結果沿Pareto前沿均勻分布。

在對相鄰個體進行選擇前，要先對Ω按子目標Fi排序，對比相鄰個體的距離與子目標Fi的距離閾值D，如果大于或等于距離閾值D，則需要對該相鄰個體對進行差分局部搜索。

4 案例研究

某港機制造企業有4個制造基地，分布在3個港口附近，并有5個部件供應商和 5個需求客戶，構成了一個4級供應鏈網絡。將供應周期劃分為3個時段。各供應商、制造基地、港口和客戶的相關數據見表1，供應鏈網絡各級節點之間的單位運輸成本及穩定性系數分別見表2和3。各港口物流能力評分分別為Θ1=0.65、Θ2=0.43、Θ3=0.57。投入產出系數θ=0.5。基于此，求出供應商的部件供應、制造基地和港口的任務分配以及港機制造企業與客戶之間的供需關系。

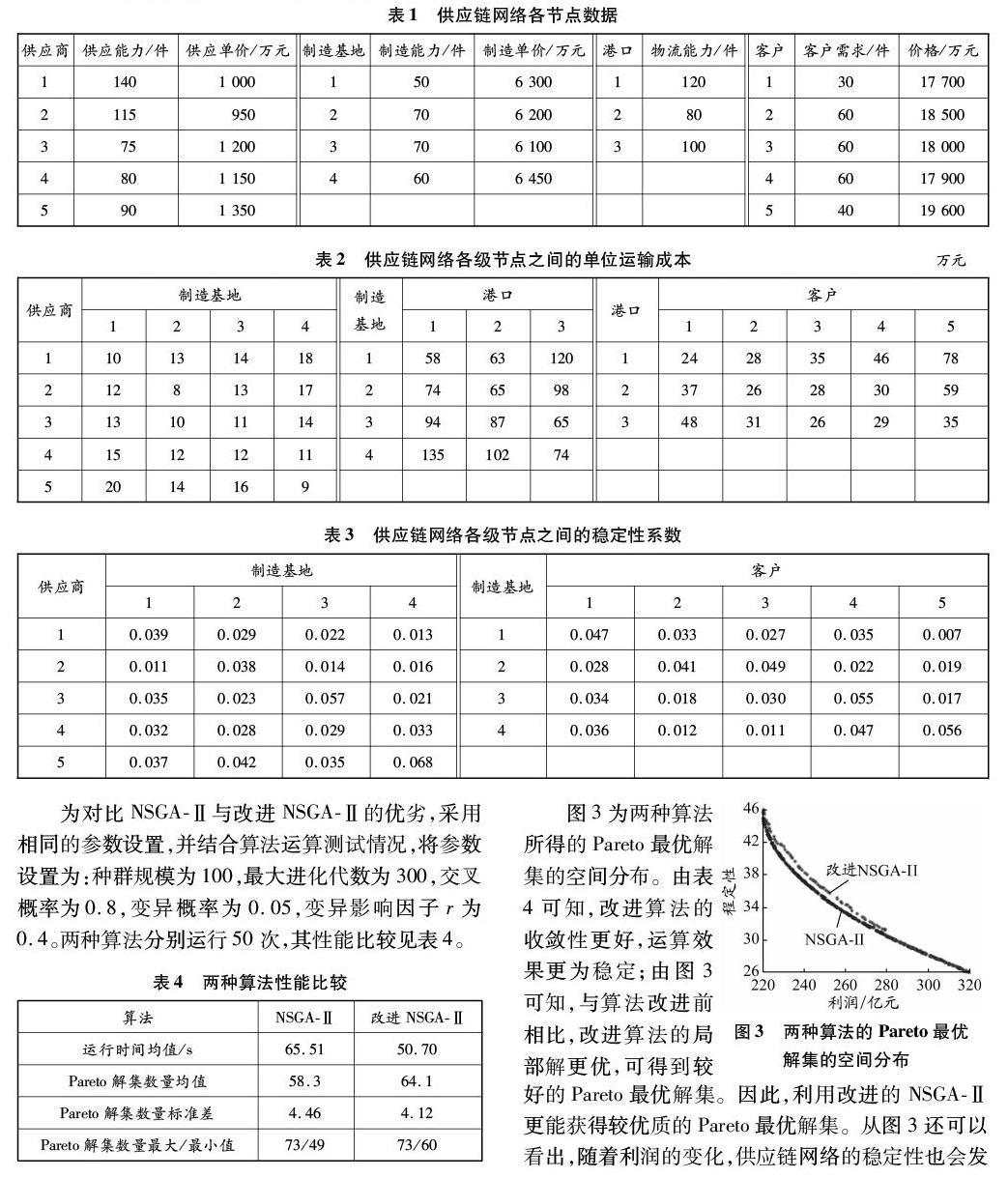
為對比NSGA-Ⅱ與改進NSGA-Ⅱ的優劣，采用相同的參數設置，并結合算法運算測試情況，將參數設置為：種群規模為100，最大進化代數為300，交叉概率為0.8，變異概率為0.05，變異影響因子r為0.4。兩種算法分別運行50次，其性能比較見表4。

解集的空間分布 ?圖3為兩種算法所得的Pareto最優解集的空間分布。由表4可知，改進算法的收斂性更好，運算效果更為穩定;由圖3可知，與算法改進前相比，改進算法的局部解更優，可得到較好的Pareto最優解集。因此，利用改進的NSGA-Ⅱ更能獲得較優質的Pareto最優解集。從圖3還可以看出，隨著利潤的變化，供應鏈網絡的穩定性也會發生變化。在實際決策中，當現實環境更穩定時，決策者更偏向于經濟成本低的方案，而當外部環境不穩定時，決策者更愿意選擇網絡穩定性高的方案。也可設置目標閾值，如當設置F1≥240億元、F2≥30時，可選擇圖3中x軸利潤大于240億元、y軸穩定性大于30所對應的Pareto最優解集中的一個解。這里，選取一個最優解F1=256.1萬元、F2=33.87，其對應的決策見表5。總之，利用改進的NSGA-Ⅱ可為決策者提供更多樣的選擇。

5 結 論

本文結合港機制造企業的實際情況，以其供應鏈網絡的經濟性和穩定性為目標建立多目標混合整數規劃模型，并結合算例對NSGA-Ⅱ進行改進。結果表明，利用該模型能使供應鏈網絡的經濟性和穩定性都得到一定的優化，且改進的NSGA-Ⅱ計算效果更好，更有助于網絡優化。本文研究也存在不足之處，具體表現在現實中供應鏈網絡各節點的狀態可能隨時間而變化，客戶需求具有隨機性、多樣性等特點，這些是下一步港機制造企業供應鏈網絡優化研究的方向。

參考文獻：

[1] LALMAZLOUMIAN M， WONG K Y， GOVINDAN K， et al. A robust optimization model for agile and build-to-order supply chain planning under uncertainties[J]. Annals of Operations Research， 2016， 240（2）： 435-470.

[2] KHALIFEHZADEH S， SEIFBARGHY M， NADERI B. A four-echelon supply chain network design with shortage： mathematical modeling and solution methods[J]. Journal of Manufacturing Systems， 2015， 35： 164-175. DOI： 10.1016/j.jmsy.2014.12.002.

[3] NEJAD A E， NIROOMAND I， KUZGUNKAYA O. Responsive contingency planning in supply risk management by considering congestion effects[J]. Omega， 2014， 48： 19-35. DOI： 10.1016/j.omega.2014.03.002.

[4] AZAD N， DAVOUDPOUR H， SAHARIDIS G K D， et al. A new model to mitigating random disruption risks of facility and transportation in supply chain network design[J]. International Journal of Advanced Manufacturing Technology， 2014， 70： 1757-1774. DOI： 10.1007/s00170-013-5404-0.

[5] 李夢. 復雜供應鏈網絡的協作同步動力學模型研究[D]. 天津： 天津工業大學， 2019.

[6] 張虹. 基于多目標決策的供應鏈網絡規劃研究[D]. 長沙： 湖南大學， 2018.

[7] SHIM V A， TAN K C， TANG Huajin. Adaptive memetic computing for evolutionary multiobjective optimization[J]. IEEE Transactions on Cybernetics， 2015， 45（4）： 610-621. DOI： 10.1109/TCYB.2014.2331994.

[8] QIU Xin， XU Jianxin， TAN K C， et al. Adaptive cross-generation differential evolution operators for multiobjective optimization[J]. IEEE Transactions on Evolutionary Computation， 2016， 20（2）： 232-244. DOI： 10.1109/TEVC.2015.2433672.

[9] 時思思， 張新燕， 王志浩. 一種基于DCD和a-tDX改進的NSGA-II算法[J]. 計算機仿真， 2019， 36（12）： 257-262. DOI： 10.3969/j.issn.1006-9348.2019.12.053.

[10] 路艷雪， 趙超凡， 吳曉鋒. 基于改進的NSGA-II多目標優化方法研究[J]. 計算機應用研究， 2018， 35（6）： 1733-1737. DOI： 10.3969/j.issn.1001-3695.2018.06.029.

[11] 吳暖， 王諾， 黃祺. 基于改進NSGA-II算法的班輪航線配船多目標優化[J]. 工業工程與管理， 2018， 23（1）： 79-85. DOI： 10.19495/j.cnki.1007-5429.2018.01.012.

[12] 褚忠偉. 某港機制造企業裝配車間精益改善研究[D]. 南昌： 南昌大學， 2019.

[13] 賴成壽. 考慮不確定性的港口供應鏈企業合作策略研究[D]. 大連： 大連海事大學， 2019.

[14] 董駿峰， 王祥， 梁昌勇. 基于個體鄰域的改進NSGA-II算法[J]. 計算機工程與應用， 2019， 55（5）： 166-174.DOI： 10.3778/j.issn.1002-8331.1711-0358.

[15] 路艷雪. NSGA-Ⅱ多目標優化算法的改進及應用研究[D]. 太原： 太原理工大學， 2017.

（編輯 趙勉）