自潤滑關節軸承襯墊彈性參數的計算

汪久根，郭 昊，洪玉芳，陳芳華

(1. 浙江大學 機械工程學院，浙江 杭州 310027； 2. 浙江省機電產品質量檢測所，浙江 杭州 310051)

襯墊關節軸承是一種球面滑動軸承，因為具有良好的承載能力、減摩抗磨能力，常用于汽車、礦山機械和航空領域[1-2]。襯墊關節軸承主要結構是一個帶內球面的軸承外圈、粘貼在軸承外圈內球面的自潤滑襯墊和一個帶外球面的軸承內圈組成。目前襯墊關節軸承的襯墊普遍采用纖維編織復合材料[3]。纖維編織復合材料是摩擦因數較小的纖維與其他材料(例如碳纖維、玻璃纖維等)通過一定的方式編織而成，與軸承內圈外球面相接觸的工作面以摩擦因數很低的聚四氟乙烯纖維(PTFE)為主，與軸承外圈內球面相接觸的黏結面以高強度、易黏附的纖維(如Kevlar纖維等)為主[4]。

襯墊宏觀上屬于正交各向異性材料，目前主要通過細觀力學方法，利用復合材料各組成部分預測其宏觀彈性性能[5]。左中鵝等[6]基于平紋織物層合板內紗線的細觀分布, 建立具有雙凸結構的特征體積單元有限元模型，通過數值分析計算復合材料模量, 并根據復合材料內纖維與基體的失效準則預測單胞強度。劉召磊等[7]通過研究玻璃纖維和碳-50基體編織織物襯墊，在剛度平均的基礎上結合幾何模型，提出了斜紋織物襯墊彈性性能解析模型。王東寧等[8]建立了平紋織物三維細觀幾何模型，對彈丸沖擊響應進行了模擬。陳紀剛等[9]用數值模擬和解析法對修正的襯墊特征體元模型進行了計算，并與實驗數據進行比對驗證。盧建軍等[10]提出了PTFE/Kevlar斜紋編織襯墊不同磨損深度下的磨損模型，并與實驗進行對比。上述研究中建立的襯墊特征體元幾何模型與實際偏差較大，且彈性參數計算值與實驗值相對誤差較大。

本文結合自潤滑關節軸承襯墊的壓緊預處理過程，對襯墊的特征體元細觀幾何模型進行了修正。在此基礎上，利用橋聯矩陣[11]，提出了改進的編織襯墊彈性參數的預測模型，并與其實驗結果進行比對，以驗證本文提出模型的準確性。

1 編織方式

纖維編織襯墊材料的編織方式主要分成機織、編織、針織3類。機織的編織方式分為平紋、斜紋、緞紋等[11]。本文采用的平紋、一上二下右斜紋(以下簡稱為斜紋)、五枚二飛緞紋(以下簡稱為緞紋)3種編織結構如圖1所示。

圖1 平紋、斜紋、緞紋襯墊結構示意圖Fig.1 Microcosmic structures of plain(a), twill (b) and satin (c) fabric liners

2 橋聯矩陣

對于復合材料，通常的做法是取特征體元進行研究。特征體元有如下特征：

1)整個復合材料可以由特征體元的重復疊加得到。

2)復合材料的等效力學量相對特征體元而言是連續或者有定義的。

特征體元是具備前2條特征的最小體積單元，相當于各向同性材料中的一個幾何點，各力學量必須相對特征體元取平均值。

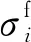
(1)

式中，Aij為橋聯矩陣，在彈性范圍內，正應力與剪應力不耦合。橋聯矩陣具有如下形式[13]：

(2)

式中：aij為橋聯矩陣元素。

本文主要用橋聯矩陣計算自潤滑關節軸承襯墊纖維束特征體元的橫向彈性模量、面內剪切模量、橫向剪切模量，從而進一步計算得到襯墊宏觀等效彈性參數。

3 編織襯墊彈性參數理論分析模型

襯墊經向和緯向纖維束都假定為橫觀各向同性，對稱軸為纖維束的軸線。近年來在對于襯墊的細觀結構研究中，纖維束截面都依照Lee等[14]給出的透鏡形狀，如圖2所示。

實際上在編織襯墊使用之前，為達到最終的高纖維體積分數，還需對襯墊進行壓緊預處理，經過有限次的加載、保持、卸載的循環之后，纖維束截面形狀和波形都發生了變化[15-18]。

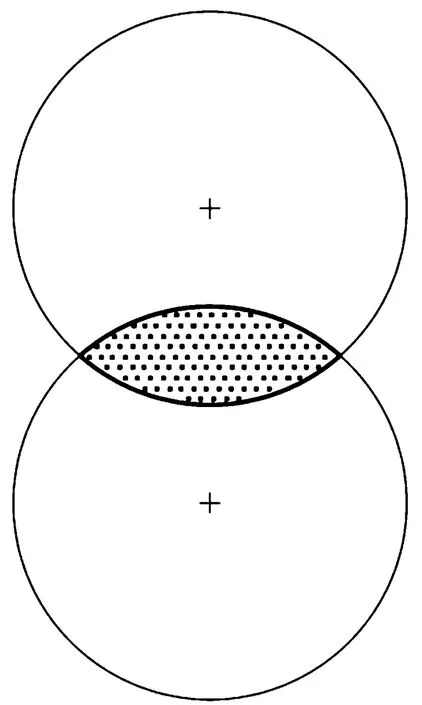
圖2 透鏡形纖維束截面示意圖Fig.2 Lenticular cross-sectional shape of yarn

以平紋編織襯墊為例，壓緊預處理前后的纖維束波形和截面形狀如圖3所示。圖中：w0、d0、H0為壓緊預處理前纖維束寬度、厚度、襯墊厚度；w、d、H為壓緊預處理后纖維束寬度、厚度、襯墊厚度。纖維束截面形狀由橢圓形變為趨近于由正弦曲線段和直線段圍成，纖維束波形由正弦曲線變為趨近于由直線段和正弦曲線段組成。

為此，提出了修正的襯墊特征單元細觀幾何模型。纖維束截面形狀如圖4所示，上下輪廓線對稱，由2曲線段和1直線段組成。為表示方便，取纖維束厚度方向為z軸，寬度方向為x軸，記纖維束厚度為d，纖維束寬度為w。

圖3 平紋襯墊壓緊預處理前后結構示意圖Fig.3 Structure of plain fabric liner before(a) and after(b) compaction preform

圖4 纖維束截面示意圖Fig.4 Cross-sectional shape and size of yarn

纖維束截面輪廓線第1條曲線段方程如下：

(3)

纖維束截面積A為：

(4)

3.1 纖維束體積分數

平紋襯墊特征體元(RVE)沿A-A的截面如圖5所示。下角標w、f、m分別表示經向纖維束參數、緯向纖維束參數、基體參數。

圖5 平紋襯墊特征單元A-A截面示意圖Fig.5 A-A cross section of RVE of plain fabric liner

dw、df分別為經向纖維束和緯向纖維束的厚度；H為特征體元厚度。

經向纖維束直線段長度

Lsw=wf+Lwg

(5)

式中：wf緯向纖維束寬度；Lwg是經向纖維束間隙。

纖維束彎曲部分長度

(6)

式中，z′為z的一階導數。

經向纖維束的總長度

Law=nLsw+Lwg+Lcw,n=1,2,3

(7)

式中，n=1,2,3，分別對應平紋、斜紋、緞紋結構。

特征體元經向長度

Lw=kLsw,k=2,4,5

(8)

式中，k=2,4,5，分別對應平紋、斜紋、緞紋結構。

特征體元內經向纖維束體積

Vw=kALcw

(9)

特征體元的體積

V=LwLfH

(10)

式中，Lf為特征體元緯向長度，Lf=Lw。

特征體元中經向纖維束的體積分數φw為：

φw=Vw/V

(11)

Vf為緯向纖維束體積，特征體元中緯向纖維束的體積分數φf為：

φf=Vf/V

(12)

因此得到特征體元中基體的體積分數φm為：

φm=1-φw-φf

(13)

3.2 襯墊彈性常數

襯墊柔度矩陣計算流程如圖6所示。

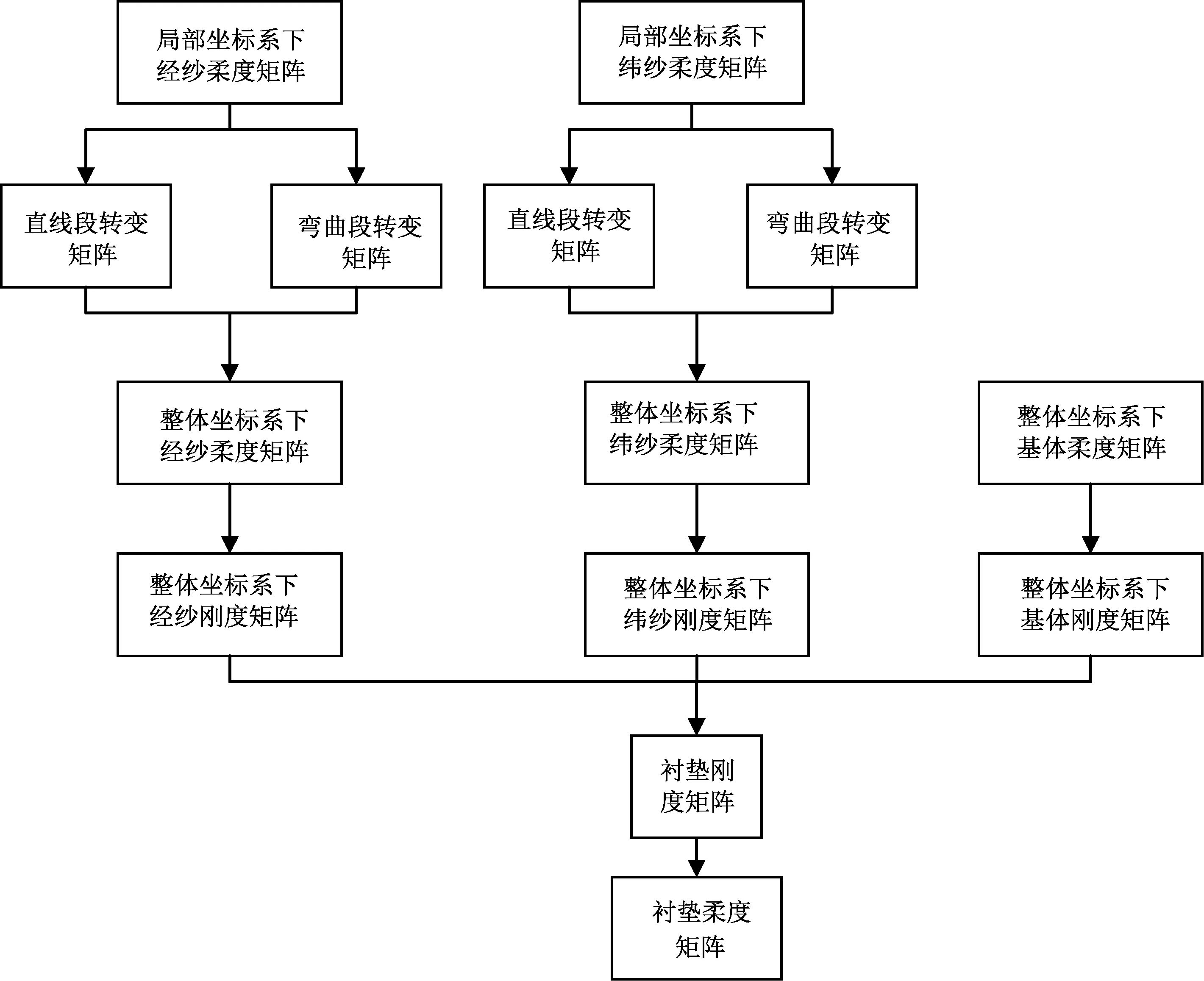
圖6 襯墊柔度矩陣計算流程Fig.6 Flow chart of compliance matrices of liners

計算經向纖維束的5個獨立彈性常數的公式如下式所示。其中：軸向彈性模量E11以及軸向泊松比ν12用Chamis模型[19]計算；橫向彈性模量E22、面內剪切模量G12以及橫向剪切模量G23用橋聯模型[12]計算。

(14)

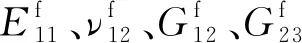
(15)

mi(i=1,2,3,4,5,6)[12]分別為：

(16)

文獻[13]給出了橋聯矩陣Aij的元素：

(17)

式中：α和β是橋聯參數，取值范圍在0～1之間[19]。對不同的纖維和基體組成的纖維束，可根據實驗測得的橫向模量和剪切模量來調節橋聯參數取值。

另外，橫向泊松比ν23可由下式求得：

(18)

經向纖維束在局部坐標系下的柔度矩陣Sij為

(19)

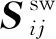
(20)

經向纖維束彎曲部分可以看成是有限個微小直線纖維束段組成，各纖維束段的局部坐標系(x1,x2,x3)與整體坐標系(x,y,z)下的柔度矩陣的轉換矩陣Tc為[20]

(21)

經向纖維束彎曲部分整體與局部坐標系關系如圖7所示。

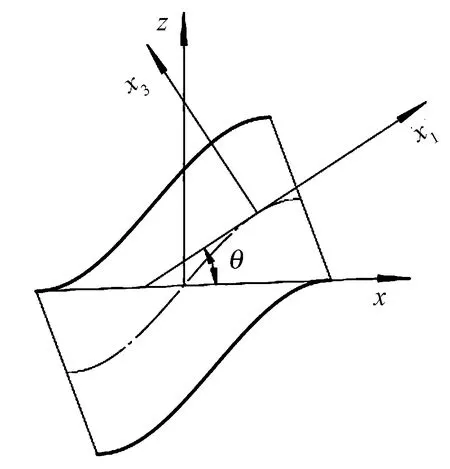
圖7 纖維束彎曲部分示意圖Fig.7 Curve part of fiber yarn

x軸與x1軸夾角θ為

(22)

由此得到經向纖維束彎曲部分在整體坐標系下的柔度矩陣：

(23)

經向纖維束直線部分和彎曲部分的長度分數λs、λc分別為：

(24)

λs=1-λc

(25)

經向纖維束整體坐標系柔度矩陣：

(26)

(27)

(28)

(29)

(30)

式中，φf為特征體元中緯向纖維束的體積分數。

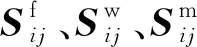
(31)

(32)

4 實驗結果對比分析

利用上述幾何模型和彈性參數計算模型，對文獻[9]中斜紋襯墊和文獻[21]中平紋、緞紋襯墊的宏觀彈性參數進行計算。

文獻[21]中平紋襯墊經向和緯向纖維束為PTFE纖維束，基體為酚醛樹脂。在Zwick/Roell公司的BZ2.5/TS1S型電子織物強力機上，以 0.2 mm/min 恒定的加載速度對平紋和緞紋襯墊試樣進行拉伸強度測試。CCD相機放置在樣品的表面，以便在加載過程中對試樣的應變進行圖像記錄，應變測量的精度為0.005%。用數字圖像相關分析方法來處理得到的順序圖像，從而得到襯墊的拉伸應力應變圖，以及平紋和緞紋襯墊的x方向和y方向彈性模量、沿x方向剪切模量。

文獻[21]中平紋和緞紋襯墊的纖維束寬度0.100 mm，厚度0.190 mm，間隙 0.067 mm，紗線填充率0.700。材料參數如表1所示。

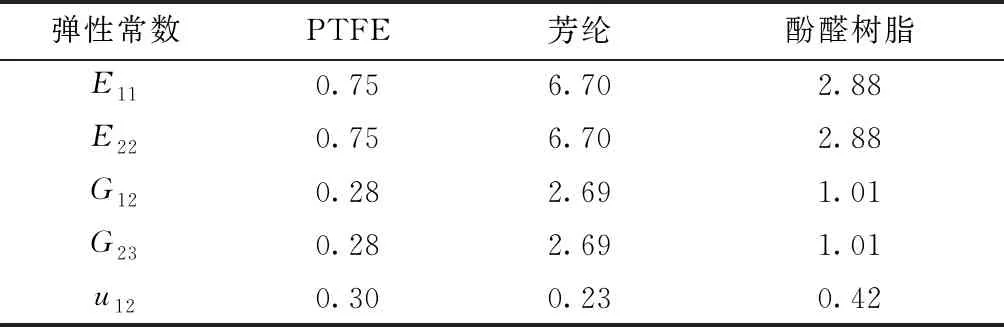
表1 平紋和緞紋襯墊材料彈性參數Tab.1 Elastic parameters of materials of plain and satin fabric liners GPa

將上述參數代入文中提出的模型計算，得到整體坐標系下平紋襯墊彈性參數。與實驗值比較結果如表2所示。綜合對比發現，經向和緯向纖維束計算中α和β分別取0.6、0.1時準確度最高，最大誤差4.76%，最小誤差0.51%，本模型計算該平紋織物襯墊的宏觀彈性參數具有可行性。

表2 平紋計算結果與實驗比對Tab.2 Comparison between computational and experimental results of plain fabric liner

文獻[9]中斜紋襯墊經向纖維束為 PTFE纖維束，緯向纖維束為芳綸纖維束，基體為酚醛樹脂。取有效寬度為50 mm、有效長度為100 mm的斜紋襯墊，在Y511B型電子織物強力機上以 20 mm/min 測試拉伸強度。在自制的實驗機上沿襯墊的布面方向進行壓縮實驗，記錄壓縮力與變形數據。依據實驗數據獲得斜紋襯墊x方向和y方向彈性模量。纖維束的幾何參數和材料參數分別如表3、4所示。

表3 文獻[9]中斜紋襯墊纖維束幾何參數Tab.3 Geometric parameters of yarn of twill fabric liner

表4 文獻[9]中斜紋襯墊材料彈性參數Tab.4 Elastic properties of materials of twill fabric liner GPa

將上述參數代入文中提出的模型計算，得到整體坐標系下斜紋襯墊彈性參數與實驗值比較，結果如表5所示。綜合對比發現，經向纖維束計算中α和β分別取0.2、0.6，緯向纖維束α和β分別取0.1、0.4時準確度最高，最大誤差5.47%，最小誤差2.58%，本模型計算該斜紋織物襯墊的宏觀彈性參數具有可行性。

表5 斜紋計算結果與實驗比對Tab.5 Comparison between computational and experimental results of twill fabric liner

文獻[21]中緞紋襯墊經向纖維束為 PTFE和芳綸纖維束，緯向纖維束為芳綸纖維束，基體為酚醛樹脂，纖維束的幾何參數與平紋襯墊相同。

將上述參數代入文中提出的幾何模型和彈性參數模型計算，得到整體坐標系下緞紋襯墊彈性參數，與實驗值結果比較如表6所示。綜合對比發現，經向纖維束計算中α和β分別取0.9、0.4，緯向纖維束α和β分別取0.4、0.9時，準確度最高，最大誤差4.39%，最小誤差小于0.01%，本模型對于計算該緞紋織物襯墊的宏觀彈性參數具有可行性。

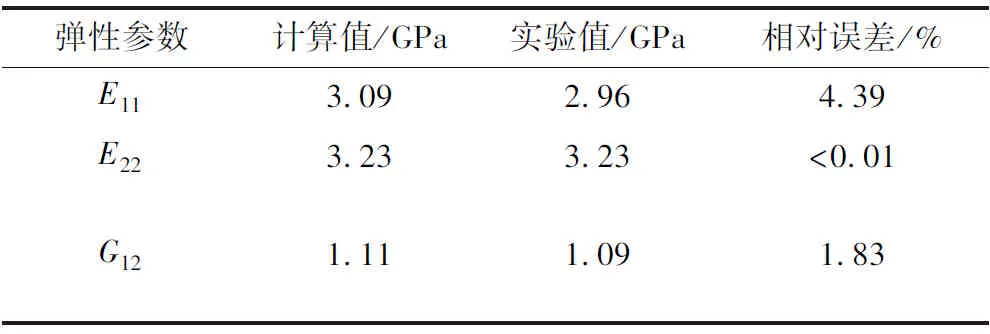
表6 5/2緞紋計算結果與實驗比對Tab.6 Comparison between computational and experimental results of satin fabric liner

用于計算不同纖維束彈性常數的橋聯參數，可通過對纖維束進行簡單拉壓剪切實驗確定。

5 結 論

本文對編織襯墊幾何模型進行了修正。利用橋聯模型提出了適用于多種編織襯墊的彈性參數解析模型。

1)通過與實驗進行比對，進行模型與計算方法的有效性驗證。結果表明，本文提出的模型得到的計算結果與實驗結果吻合性較好。

2)在運用本文提出模型計算編織襯墊彈性參數時，若纖維束中纖維和基體沿軸線方向彈性模量比值較大，所得結果較為準確。后續可對襯墊纖維束進行拉壓剪切實驗來確定橋聯參數值。

3)通過此方法獲得的結果，為襯墊軸承的磨損分析提供襯墊宏觀彈性參數，可用于自潤滑關節軸承進一步研究中。