論高中數學解題中構造函數的有效應用

李 鳴

(安徽省廣德中學 242200)

構造函數法是高中數學中轉化思想應用的重要體現，將抽象復雜的問題轉化成學生熟悉的問題，實現題目的快速準確解答.在構造函數法應用時，需要對數學題目中的已知條件和求解問題進行分析，之后進行相應的函數構造，結合題目中的條件和結論，明確解題思路和方式，有效解答數學問題.構造函數法是高中數學解題中的重要方式，應用較為廣泛，在實際的應用中，應當準確把握其中的數量關系，有效利用函數性質，解決相關數學問題.

一、借助構造函數法，解決不等式證明問題

不等式是高中數學的重要內容，并且和其他數學知識有著密切的聯系.不等式證明問題是不等式題目中的重要類型，利用題目中的已知內容，完成題目的證明.對于一些不等式證明問題，如果直接從題目已知進行分析證明，其難度比較大，甚至不能夠證明.面對這樣的情況，可以引導學生對不等式進分析，根據其結構形式構造函數，利用函數單調性進行證明，完成不等式證明問題的求解.

在高中數學不等式證明題目解答中，需要對題目進行觀察和分析，根據題目的類型，靈活引入構造函數法，明確解題思路，利用函數的性質，完成不等式證明問題解答.

二、利用構造函數法，解決方程問題

對于高中學生來說，方程并不陌生，從小學到初中，再到高中，方程是重要的知識內容，也是學生學習的重點內容.高中數學方程知識更加復雜，題目類型復雜多變，解題難度增加.同時方程題是高考中的必考題目，應當重視數學方程問題分析，提高學生解題效率，準確解答方程問題.部分方程題目較為復雜，很難做到直接求解，因此，借助構造函數法，對方程問題進行轉化，降低方程解題難度，有效解決方程問題.

例2解方程：3x+4x+5x=6x.

分析在此題目中，方程的形式比較特殊，不能合并，也不能分解.對于此種類型的題目，根據方程和函數的關系，構建相應的函數，明確解題思路，完成方程求解.

三、借助構造函數法，解答幾何問題

幾何問題是高中數學的難點問題，要求學生具備一定的空間想象能力和思維能力，能夠完成數與形的靈活轉化，有效解答幾何問題.在高中數學幾何問題解答中，對題目已知條件進行分析，繪制相應的圖形，做出深入的分析，引入函數構造法，明確解題思路，有效解答幾何問題.

解對于問題(1)，根據題目中的已知條件可以完成求解.

綜上，恒有g(x)>0(x≠1).因此除了切點外，整個曲線C都處于切線l的下方.

在幾何問題解答中，需要對其問題類型進行分析，一些問題看似是幾何問題，但是使用幾何方式很難解題，需要引入構造函數法，明確題目解題思路，準確、快速解答問題.

四、利用構造函數法，解答數列問題

數列是高中數學的重要知識內容，知識點比較多，題目類型也是復雜多變.同時，在實際的數列問題中，常常和其他知識結合，使得數列問題難度增加，對于學生來說，想要快速解題難度比較大.因此，作為教師，需要引導學生分析數列問題，靈活引入構建函數法，對問題進行轉化和思考，有效解決數列問題.

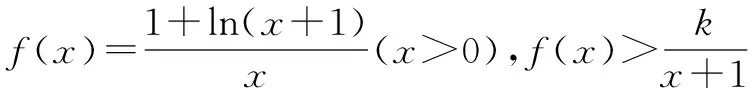
分析在此題解答時，需要根據數列內容構造相應的輔助函數，根據函數性質，利用不等式放縮原理，對原數列進行相應的轉化，有效利用函數性質，完成題目求解.

構造函數需要以函數概念的理解和掌握作為基礎，掌握函數的性質，在構造時，需要選擇合適的函數形式，準確利用函數性質，保證數學問題可以準確解答.高中數學課堂中，函數是學生學習的重點內容，構造函數法是學生需要掌握的解題方式，借助函數構造簡化解題步驟，提高解題效率.因此，高中數學課堂中，應當加深函數概念和性質理解，選擇合適的函數模型，有效解決數學問題.