火箭發動機渦輪葉片動態響應計算及方法

任 眾，許開富，朱東華

(西安航天動力研究所，陜西 西安 710100)

0 引言

渦輪葉片作為火箭發動機的關鍵部件，要求其在高溫、高負荷、高轉速的工作環境下安全可靠地工作。局部進氣的沖擊式渦輪為液體火箭發動機中常見的一種渦輪形式，工作過程中葉片受到周期性高速氣流激振力的沖擊作用，其振動及疲勞問題十分突出和復雜[1-2]。

現有的液體火箭發動機渦輪由于工作時間短，設計過程中主要考慮氣動性能及靜強度[3-5]，很少考慮由氣體激振引起的葉片振動疲勞問題。但隨著可重復使用發動機的研制，要求各零部件的服役時間成倍增加，因此，必須對渦輪葉片的高周疲勞問題開展深入的研究。而該問題的核心就是分析葉片在氣流激振力作用下的動態響應，獲得其振動應力[6-7]。

目前，葉片的動態響應計算分析主要有兩種方法。一種是理論模型的方法，將葉片簡化成懸臂梁，根據不同的氣流激振力的形式獲得激振力的簡化模型，再建立梁的彎曲振動微分方程，求解方程[8-11]；另一種是三維仿真的方法，首先通過三維非定常流場仿真獲得激振力的時域分布，再進行葉片在激振力作用下的振動響應仿真計算[12-13]。其中，第一種方法已在風機葉片及航空發動機壓氣機葉片中得到了成熟的應用[14-16]，其激振力形式為連續周期性變化的，但局部進氣的沖擊式渦輪的氣流激振力形式有著明顯的不同，其激振力形式為周期性脈沖變化，同時氣流的沖擊馬赫數也要高得多，由該激振力產生的動態響應規律會有所不同。目前，對于該種形式的激振力作用下的渦輪葉片動態響應的研究文獻較少；而第二種方法理論上可以得到準確的葉片振動響應情況，但涉及到多學科的仿真分析，計算工作量大，占用資源多，計算時間長，不利于工程設計階段對疲勞問題的快速評估。

本文提出了一套針對局部進氣沖擊式渦輪葉片動態響應的理論計算模型，并以某液體火箭發動機渦輪為研究對象，采用該方法進行葉片在流體激振力下的動態響應計算，并與三維仿真結果對比，驗證結果的準確性，為發動機渦輪高周疲勞設計提供依據。

1 計算方法

1.1 理論模型

1.1.1 受迫振動微分方程

本文的理論模型以懸臂梁受迫振動理論為基礎[17-19]。由于渦輪葉片主要是受氣動彎矩的作用產生彎曲變形，同時液體火箭發動機渦輪葉片大多數為較短的直葉片，剪切變形以及截面繞中性軸轉動慣量對葉片振動的影響較大。因此，將葉片簡化成等截面的鐵木辛柯懸臂梁，并考慮離心力及阻尼的影響，推導得到梁的受迫振動微分方程為

(1)

初始邊界條件

位移邊界條件

y(0,t)=0,y′(0,t)=0,y″(l,t)=0,y?(l,t)=0

其中

f(x,t)=f1(x)·f2(t)

式中：y為梁的位移；x為梁的軸向坐標；t為時間；E為彈性模量；G為剪切模量；ρ為密度；I為截面主慣性矩；J為單位長度梁對截面中性軸的轉動慣量；k為截面形狀因子，對于矩形截面，k=5/6；A為截面面積；l為梁的長度；c為黏性外阻尼系數；Fa為葉片離心力大小，由于實際工作過程中葉片的離心力沿葉高是變化的，為了使方程有理論解，假設葉片各截面的離心力均為平均離心力；ω為轉速；At為葉片截面面積；Rt為葉頂半徑；Rh為葉根半徑；f(x,t)為葉片單位高度所受的激勵力大小；f1(x)為氣流激振力沿葉高的分布函數;f2(t)為單位氣流激振力隨時間的分布函數。

函數f1(x)通過圖1中的葉片通道的控制體動量守恒可得[20]

ρg2(x)Ca2(x)Cu2(x)]

(2)

(3)

p=ρgRTg

(4)

式中：下標1為葉片入口截面參數；下標2為葉片出口截面參數；Zb為葉片數；ρg(x)為氣流密度的徑向分布；Ca為氣流軸向速度的徑向分布；Cu為氣流軸向速度的徑向分布；p為氣體壓力；Tg為氣體溫度；R為氣體常數。

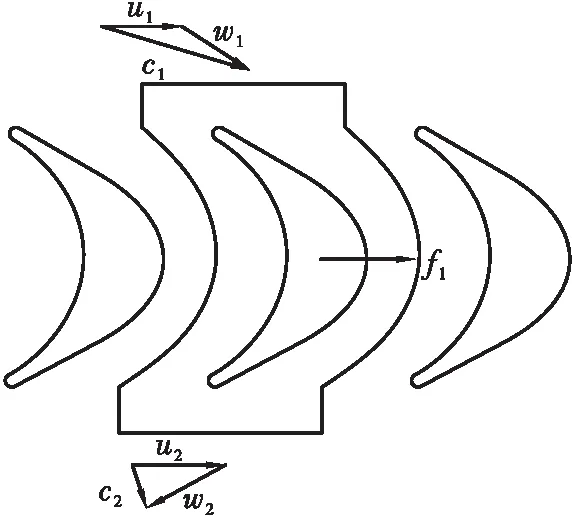
圖1 葉片通道控制體示意圖Fig.1 Schematic diagram of blade channel control body

函數f2(t)的分布如圖2所示，其中局部進氣1個周期內流體激振力的作用時間

Δt=εT

(5)

式中：ε為渦輪局部進氣度；T為1個旋轉周期的時間。

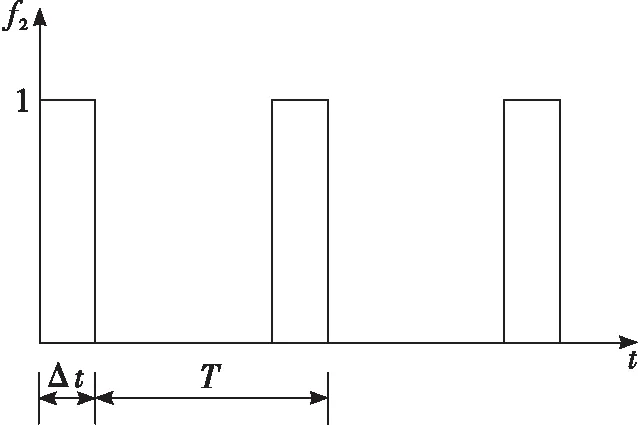
圖2 激振力的時間分布函數Fig.2 Time distribution function of excitation force

1.1.2 方程求解方法

采用模態疊加法求解式(1)，求解的形式可表示為[17]

(6)

式中：Yi(x)為梁的第i個主振型函數；qi(t)為第i個廣義坐標權函數。在實際求解時，取前3到5階振型疊加就可得到足夠精確的結果。其中，各階主振型函數即為梁的自由振動的解，令式(1)右側的激振力為零，再結合懸臂梁的位移邊界條件(3)，推導得到梁彎曲振動的特征

(7)

式中λ1、λ2分別為特征方程A1X4+B1X2+C1=0的兩個非負解。其中

C1=-ω_i2ρA

求解上述方程的第i個解ω_i，即為梁的第i階固有頻率，對應的振型函數

Yi(x)=[cosh(λ1x)-cos(λ2x)]+

(8)

為了求解各廣義坐標下的權函數，將式(6)代入式(1)，并利用振型函數的正交性，推導得

(9)

其中

式(9)左側為標準的阻尼系統的受迫振動方程，而右側可看做振幅為D2的周期激振力。將該激勵力看做一系列的微脈沖組合，利用杜哈梅積分，得到梁對該激振力的響應

qi(t)=eat[X1cos(bt)+X2sin(bt)]+

(10)

其中

系數X1、X2根據初始條件(2)確定。獲得了梁的位移響應分布y(x,t)，可利用材料力學中的關系獲得某點A的應力

(11)

式中yA為A點距截面彎曲主軸的距離。

1.2 三維仿真的方法

三維仿真的計算流程見圖3，由圖可知，整個計算流程包括CFD非定常計算、載荷傳遞、動態響應計算分析3部分。首先對渦輪整周模型進行三維瞬態流場仿真，獲得某個葉片表面的壓力分布隨時間的變化，即葉片的氣體激振力；然后通過插值運算，將流固交界面上的流場壓力映射到葉片表面的有限元網格節點上；再進行葉片的動態響應計算計算，獲得葉片在激振力作用下的響應情況；在此基礎上，結合材料的疲勞性能數據，可以做葉片的高周疲勞分析。整個計算過程在ANSYS Workbench平臺下完成。

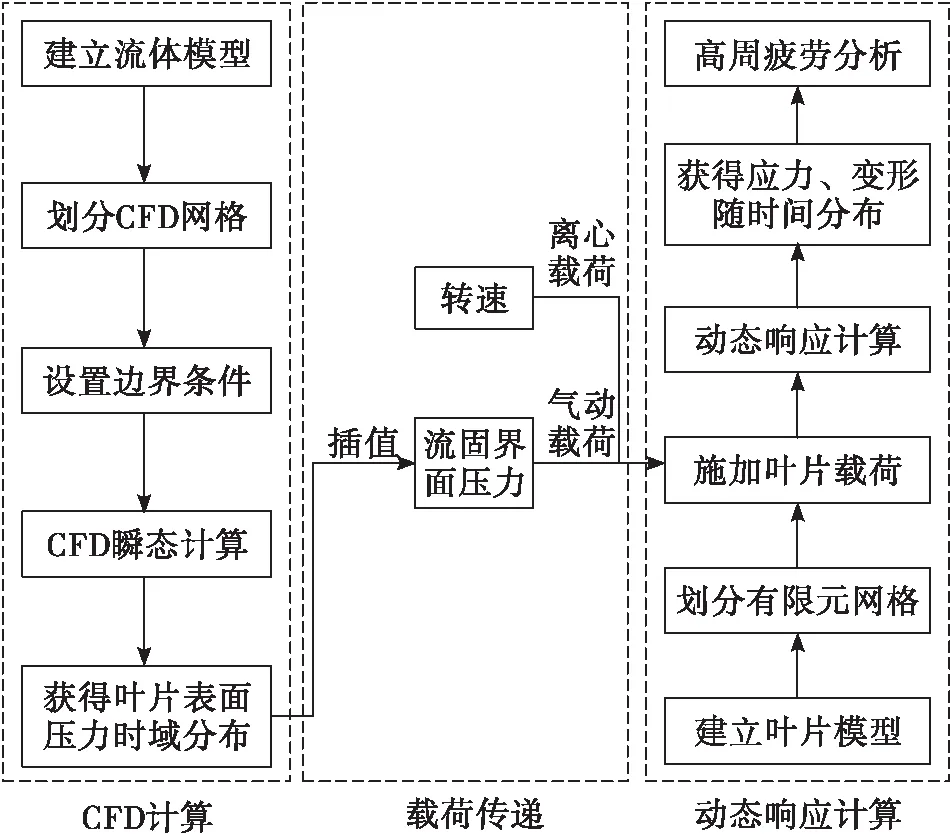
圖3 三維仿真計算方法Fig.3 Calculation method of 3D simulation

2 算例分析

2.1 研究對象

本文以某發動機渦輪為研究對象，計算葉片在氣體激振力下的動態響應。該渦輪為單級局部進氣沖擊式渦輪，工作時高溫高壓燃氣通過單個噴嘴加速，噴出的高速氣流沖擊渦輪葉片做功。其中，葉片的三維模型見圖4(a)，由圖可知，葉片為直葉片，主要幾何參數如表1所示。

表1 渦輪葉片主要幾何參數Tab.1 Main geometric parameters of turbine blades

渦輪葉片材料為高溫合金，密度為8 240 kg/m3，工作溫度下的彈性模量為146 GPa，泊松比為0.33，屈服極限為860 MPa。

2.2 理論模型求解

根據截面慣性矩相等，將渦輪葉片簡化為矩形截面的懸臂梁，如圖4所示。簡化梁的長L、寬W、高H分別為29.5、9.45、5.44 mm。此外，由于液體火箭發動機渦輪葉片短，剛性大，一般將葉片和盤考慮為一個葉盤系統，因此本文單獨將葉片簡化為梁結構，未考慮輪盤的阻抗作用，計算結果與實際存在一定的偏差。

圖4 葉片模型簡化Fig.4 Blade model simplification

首先對梁進行模態計算，計算得到的前三階固有頻率如表2所示，相應的振型如圖5所示。由表2可知，理論模型計算的固有頻率比三維仿真值偏小，一方面是由于理論模型中假設葉片各截面的離心力均為平均離心力，從而導致旋轉剛化作用對固有頻率影響的差異；另一方面是由于理論模型將葉片截面簡化為矩形截面，截面形狀的不同也會導致固有頻率的差異。

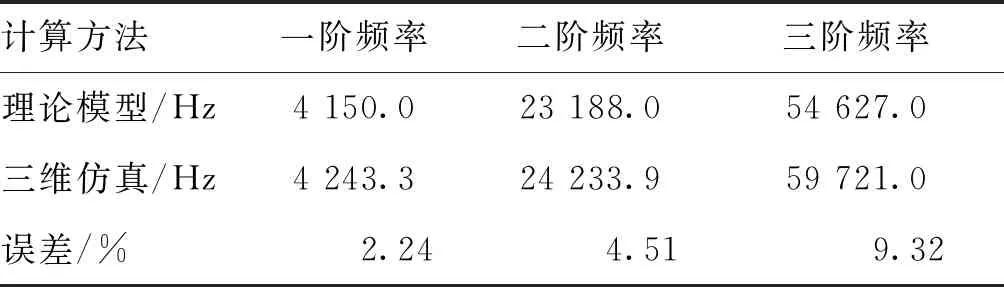
表2 葉片前三階頻率對比Tab.2 Comparison of the first three frequencies of blades

圖5 梁的前三階振型Fig.5 The first three modes of beam

然后采用模態疊加法求解梁在氣流激振力作用下的位移響應及應力響應，其中，由理論方法得到的氣體激振力載荷沿葉高的分布規律如圖6所示，該激振力在1個旋轉周期內的作用時間為0.3 ms；為了對兩種方法進行精確比較，理論模型與三維仿真的阻尼系數均取0.2。對前三階的模態振型疊加，提取了梁的根部A點的應力及頂部B點的位移結果，A點和B點的位置示如圖7所示。梁在3個周期內的頂部位移響應如圖8中的虛線所示，根部的應力響應如圖9中的虛線所示。

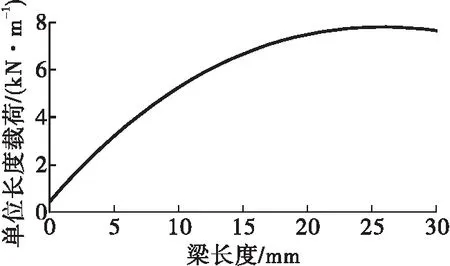
圖6 梁的激振力分布圖Fig.6 Distribution of excitation force on beam

由圖8可知，在一次氣流激振力的沖擊作用下，葉片的響應頻率約為4 066 Hz，同時由于阻尼的作用，響應幅值逐漸衰減，經歷7個振蕩后振幅基本衰減到零，每個旋轉周期內該響應重復1次。以該發動機為例，在單次工作時間范圍內大約經歷40萬次上述循環過程；由圖9可知，葉片根部的平均應力約為295 MPa，在氣流沖擊后的第一個響應動應力幅值最大，約為155 MPa，然后由于阻尼的作用動應力幅值逐漸衰減到零。

圖7 位置示意圖Fig.7 Location diagram

圖8 頂部位移響應結果Fig.8 Response results of top displacement

圖9 根部應力響應結果Fig.9 Response results of root stress

2.3 三維仿真求解

渦輪的流場三維仿真模型及邊界條件見圖10。由圖可知，計算域由噴嘴通道與動葉通道兩部分組成。整個計算域均采用結構網格，單元總數475萬。噴嘴入口為總壓邊界，動葉出口為靜壓邊界，級間采用瞬態轉靜交接面，其余均為無滑移絕熱壁面邊界。利用商用軟件CFX開展瞬態仿真計算，每個葉片通道設置5個時間步，一共計算10個旋轉周期，采用SST湍流模型及高階差分格式對方程進行離散求解。

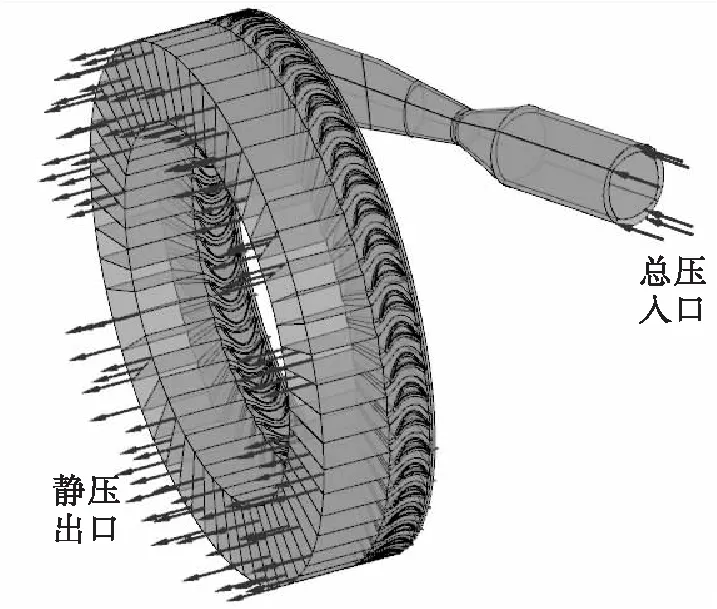
圖10 流場計算模型及邊界Fig.10 CFD model and boundary

計算得到的葉片通道內的馬赫數分布如圖11所示，由圖11可知，一周大概8個葉片受到高速氣流的沖擊作用。單個渦輪葉片受到的氣動彎矩分布如圖12所示，由圖12可知，單個葉片在一個旋轉周期內受到氣流的作用時間比例約為0.155，與式(3)計算的作用時間基本吻合，載荷的形狀接近圖2的方波。

圖11 葉片通道馬赫數分布Fig.11 Mach number distribution of blade passage

通過上文的非定常流場仿真，獲得了葉片的激振力，在此基礎上開展動態響應仿真。有限元計算模型及邊界如圖13所示。由圖13可知，模型由葉片及底座兩部分組成，均采用六面體結構網格進行劃分，網格節點1.25萬。首先對葉片進行模態分析，通過對比各階頻率的大小來驗證理論梁模型的準確性。然后利用商用軟件ANSYS DYNA進行葉片的動態響應仿真，獲得葉片的位移及動應力響應分布。

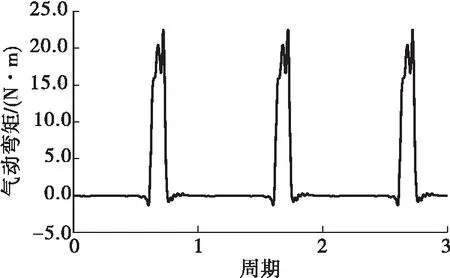
圖12 葉片氣動彎矩分布Fig.12 Distribution of aerodynamic bending moment of blade

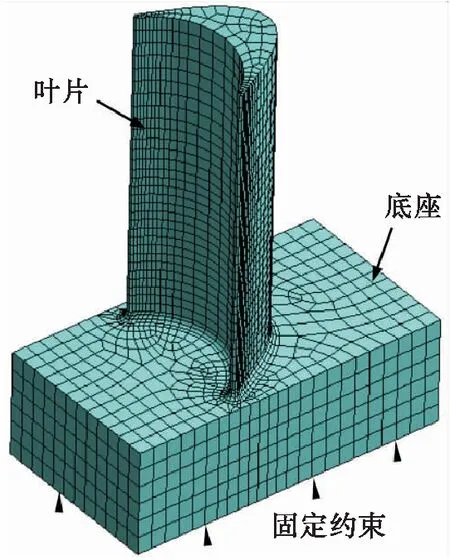
圖13 有限元模型及邊界Fig.13 FEM model and boundary

模態計算得到的葉片前三階固有頻率如表2所示，由表2可知，三維仿真計算得到的固有頻率比理論模型偏大，且隨著階次的增大，偏差逐漸增大，但最大誤差不超過10%，說明采用理論梁模型對葉片進行簡化的準確性。

計算得到的葉片根部應力響應如圖9中的實線所示，由圖9可知，三維仿真得到的平均應力約為305 MPa，響應頻率為4 000 Hz，響應動應力的最大幅值為175 MPa。與理論模型方法相比，動應力平均值、頻率及最大幅值誤差分別為3.39%、1.62%、11.4%，從而驗證了理論模型進行葉片動態響應計算的準確性。

3 結論

本文建立了一套針對局部進氣沖擊式渦輪葉片的動態響應的理論計算模型，并以某液體火箭發動機渦輪為研究對象，分別采用理論模型的方法與三維仿真的方法計算了葉片在氣流及激振力作用下的動態響應。主要結論如下：

1)根據液體火箭發動機渦輪葉片的特點，將葉片簡化成等截面的鐵木辛柯懸臂梁，同時考慮離心力及阻尼的影響，推導得到梁的受迫振動微分方程，并采用模態疊加法對方程進行求解。

2)采用流固耦合的方法對葉片動態響應進行三維仿真，首先通過非定常全流場仿真獲得氣流激振力，在此基礎上開展葉片的三維有限元模態分析及動態響應分析。

3)與三維仿真計算方法對比，采用理論模型方法計算得到的葉片固有頻率誤差不超過10%，同時根部平均動應力低3.39%，響應頻率高1.62%，響應最大幅值低11.4%。驗證了該理論模型的準確性，可以采用該方法開展發動機渦輪葉片高周疲勞設計。