基于改進人工勢場法的移動機器人路徑規劃

徐小強，王明勇，冒 燕

（武漢理工大學自動化學院，武漢430070）

（?通信作者電子郵箱maoyan@whut.edu.cn）

0 引言

路徑規劃是指存在障礙物的環境下，按照一定的性能指標，機器人如何從所處的環境中搜索到一條從初始位置到終點的安全的、無碰撞的最優或次優路徑［1］。常用的算法有蟻群算法［2-3］、Dijkstra算法［4-5］、A*算法［6-7］、粒子群法［8］、遺傳算法［9-10］、人工勢場法（Artificial Potential Field method，APF）［11-14］等算法。蟻群算法、Dijkstra 算法、A*算法、遺傳算法等算法存在運算時間長、迭代次數多，在未知環境下規劃的實時性不好等問題。人工勢場法在進行路徑規劃時，不需要提前生成完整路徑，只需要根據當前姿態以及周邊障礙物來確定下一步的運動，算法反應速度快、計算量小，便于實時性控制，且規劃出的路徑平滑安全［15］。但是傳統人工勢場法容易陷入局部極小點，且當障礙物環繞時，容易陷入陷阱區域，當路徑中存在局部極小點或者陷阱區域時，傳統人工勢場法無法規劃出完整的路徑。

為此，文獻［16］通過“沿邊走”的方法來解決局部極小點和復雜障礙物環境下的路徑規劃問題，但規劃出的路徑太長。文獻［17］對障礙物連通性進行了分析，并設立臨時目標點來幫助機器人脫離局部極小點，該算法雖然可以減少搜索空間，提高搜索效率，但沒有考慮U 型陷阱的情況。文獻［18］提出了一種基于電勢場的路徑規劃算法，可以避免陷阱問題，但其建模過程復雜、計算量大。文獻［19］提出在扇形分區設置臨時障礙物的方法，打破局部極小點的平衡，幫助機器人脫離局部極小狀態，但是臨時障礙物的位置選取過于粗略，規劃出的路徑不夠簡短。文獻［20］通過引入方向向量和虛擬目標點的方法，幫助機器人逃離局部極小點和陷阱區域，但是在虛擬目標點的選取上不太合理，導致規劃出的路徑較長且存在拐角過大情況。

針對上述算法存在的問題，本文通過引入安全距離，對障礙物進行一定的篩選，減少規劃出的路徑長度；引入預測距離，通過提前改變前進方向，避免陷入陷阱區域、局部極小點或者發生碰撞；通過設置虛擬目標點，引導機器人避開以上情況，安全到達終點。最后利用Matlab 對本文算法——提前預測人工勢場法（Artificial Potential Field Method with Advance Prediction）進行了可行性驗證。

1 人工勢場法存在的問題

根據文獻［11-14］可知，傳統人工勢場法規劃路徑時會存在以下問題：

1）當路徑中障礙物產生的斥力與目標點產生的引力大小相等、方向相反時，機器人將陷入局部極小點，無法完成整個路徑的規劃，如圖1（a）。

2）當目標點附近有障礙物時，由于靠近目標點，目標點對機器人的引力很小，此時障礙物的斥力大于目標點的引力，會使機器人在目標點附近抖動，無法達到目標點，如圖1（b）。

3）當存在復雜障礙物環境，如U型障礙物時，機器人被障礙物環繞，無法逃出，從而導致路徑規劃失敗，如圖1（c）。

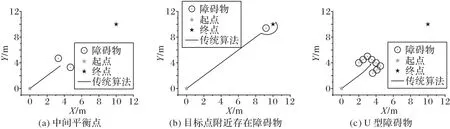
圖1 局部極小點和U型障礙物Fig.1 Local minimum and U-shaped obstacle

針對傳統人工勢場法容易出現圖1 所示的問題，提出了一種改進算法——提前預測人工勢場法，可以很好地解決上述問題。該算法對斥力的生成機制做出調整，在一定條件下對前進方向做出了改進，通過設置虛擬目標點引導機器人到達終點。

2 改進算法

2.1 障礙物處理

為了便于實際路徑規劃，對環境中的障礙物進行一定的處理，將所有障礙物分割成若干個圓形障礙物，圓的半徑為Ro，要求圓形障礙物將原障礙物全覆蓋且兩個鄰近的圓形障礙物圓心之間的距離小于2Ro，如圖2 所示。為了安全，對圓形障礙物進行膨脹處理，處理后的半徑為Rc，要求機器人到圓形障礙物的圓心距離即安全距離rs大于Rc。

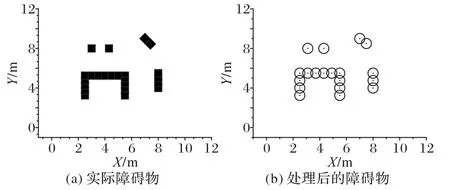
圖2 障礙物的處理Fig.2 Processing of obstacles

2.2 安全距離rs

傳統人工勢場法路徑規劃過程中，機器人從當前位置本可以以直線前進安全到達目標點，但是卻由于直線路徑上的一些點在障礙物的影響范圍內，導致機器人在斥力的作用下走了彎路，這樣規劃出來的路徑長度就有所增長，導致規劃出的路徑不是最優路徑。針對這一問題，在計算斥力時引入安全距離，使機器人避免不必要的斥力作用。

在路徑規劃的過程中，計算障礙物到當前點與目標點連線的距離di，如果di小于等于rs，說明以當前方向前進會發生碰撞，此時需要考慮該障礙物的斥力；如果di大于rs，說明以當前方向前進不會發生碰撞，此時不考慮此障礙物的斥力，繼續沿當前直線前進，規劃出來的路徑平滑且較短，如圖3所示。

圖3 障礙物無碰撞風險Fig.3 No collision risk of obstacles

針對圖1（a）的問題，引入安全距離后的算法可以很好地解決，如圖4 所示，由于兩個障礙物均在安全距離以外，所以不會對機器人產生斥力作用，機器人沿當前方向前進。

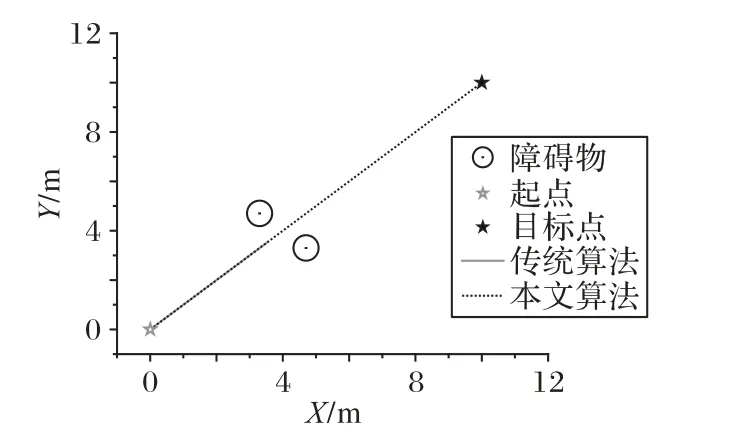
圖4 解決中間平衡點問題Fig.4 Solving problem of intermediate equilibrium point

2.3 當前點到目標點的距離ri

當目標點附近存在障礙物時，機器人所受的斥力很可能會大于等于引力，這樣就會導致機器人在目標點附近震蕩或停止，無法到達目標點，如圖1（b）所示。

針對圖1（b）的問題，在斥力公式中添加因子，ri為當前點到目標點的距離，機器人在目標點附近時，ri很小，傳統人工勢場法斥力公式乘以，得到一個較小的斥力值，使機器人所受合力指向目標點，機器人能夠順利到達目標點，如圖5所示。

圖5 解決目標點附近存在障礙物問題Fig.5 Solving problem of having obstacle near target point

2.4 改進后的算法

通過上述分析可知：

1）當移動機器人在障礙物影響范圍之外或者移動機器人前進方向安全時，移動機器人受到的斥力為零，在引力的作用下，朝著目標點前進。

2）當移動機器人在障礙物影響范圍內，且前進方向存在碰撞風險時，障礙物會對移動機器人產生斥力作用，阻礙移動機器人碰撞障礙物。為了確保移動機器人不會碰撞障礙物，引入當前位置到障礙物距離的倒數與障礙物影響范圍距離的倒數之差，即，可知：當移動機器人距離障礙物越近時，ρo-ρi越大，ρi ρo越小，所以越大，產生的斥力就越大，阻礙移動機器人駛向障礙物；當移動機器人與障礙物之間的距離小于1 時，急劇增大，產生較強的斥力作用，進一步阻止移動機器人碰撞障礙物；當移動機器人快要到達目標點，且目標點附近存在障礙物時，由于引力作用太弱，斥力作用太強，移動機器人無法到達目標點，此時可以通過減小斥力作用使移動機器人順利到達目標點。引入因子，ri為當前點到目標點的距離，移動機器人在目標點附近時，很小，斥力公式乘以，得到一個很小的斥力值。

改進后的斥力公式為：

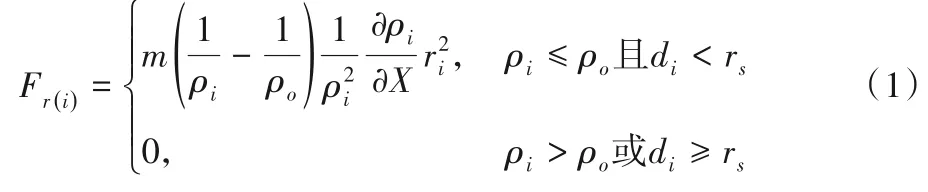
其中：m表示大于零的斥力場常量；ρi表示當前位置與障礙物的距離；ρo表示單個障礙物影響的最大范圍距離；ri表示當前位置與目標點的距離；rs表示安全距離；di表示障礙物到當前點與目標點連線的距離。

2.5 預測距離Rp

當地圖中存在陷阱區域時，如U型障礙物，傳統人工勢場法會陷入其中，產生震蕩或停止，無法規劃出完整的路徑，如圖1（c）所示。

針對圖1（c）的問題，引入預測距離Rp，計算目標一側的障礙物到當前方向所在直線的距離di，當di小于等于安全距離rs時，取滿足以上條件且到當前點的距離最近的障礙物為中心障礙物，計算此障礙物到當前點的距離為Rx。判斷Rx是否小于等于預測距離Rp，若不是，則沿當前方向繼續前進；若是，則以Rx為半徑、當前點為圓心向障礙物少的一側旋轉。為了使規劃出的路徑較短，每次旋轉3°，每旋轉一次，就判斷各障礙物到當前點的距離di，當所有di都大于安全距離rs時，停止旋轉，以此時的方向為新的前進方向，以半徑的另一端點作為新的虛擬目標點。通過合理地選取預測距離Rp的大小，可以在機器人陷入陷阱區域之前就改變前進方向，避開陷阱區域，規劃出來的路徑較短，且由于每次旋轉的角度很小，規劃出來的路徑比較平滑，如圖6所示。

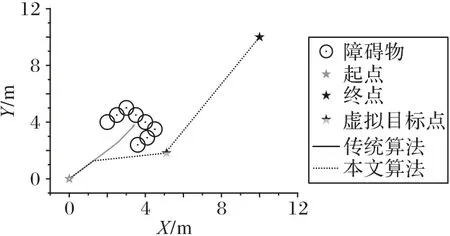
圖6 解決U型障礙物問題Fig.6 Solving problem of U-shaped obstacle

2.6 算法流程

提前預測人工勢場法的算法流程如下：

步驟1 算法初始化，設置機器人初始位置Xo和終點位置Xg，給定相關參數：障礙物影響范圍ρo、引力常數k、斥力常數m、步長l、安全距離rs、預測距離Rp。

步驟2 連接當前點與終點，得到一條直線，判斷各障礙物到此直線的距離d。

步驟3 如果障礙物在目標一側，同時滿足障礙物i到直線的距離小于安全距離rs且障礙物i到當前點的距離最短，執行步驟4；否則，沿當前方向前進，直到達到終點。

步驟4 判斷步驟3 中障礙物i到當前點的距離，如果小于預測距離Rp，執行步驟5；否則，沿當前方向前進，直到小于預測距離Rp。

步驟5 以障礙物i與當前點的距離為半徑向障礙物少的一邊旋轉，每次旋轉3°，直到目標一側所有障礙物到新的方向所在直線的距離大于安全距離rs，則以此時的方向為新的前進方向，半徑的另一端點作為新的目標點，并沿新的方向前進。

步驟6 判斷是否到達新的目標點，如果到達新的目標點，則跳到步驟2，直到到達終點；否則，沿當前方向繼續前進，直到到達新的目標點。

3 算法仿真及結果分析

為驗證本文算法的可行性以及路徑規劃的效果，在神舟筆記本電腦Z7M-CT5NA 上通過Matlab 進行仿真研究，Z7MCT5NA 的硬件信息如下：Core i5-9300H、2.4 GHz 四核處理器，8 GB 內存，512 GB 固態硬盤。將機器人視為一個質點，初始參數設置如下：機器人初始位置Xo=(0，0)，終點位置Xg=(10，10)，障礙物影響范圍ρo=2.5，引力常數k=15，斥力常數m=10，步長l=0.1，安全距離rs=0.6，預測距離Rp=4。

由于障礙物的特點對機器人的路徑規劃有較大的影響，所以在相同的障礙物環境下，對本文算法與傳統人工勢場法、文獻［19］中的算法（記作B-APF）以及文獻［20］中的算法（記作C-APF）進行多次比較，以驗證本文算法的優越性。

隨機生成的存在陷阱區域以及局部極小點的仿真地圖如圖7 所示，幾種算法在同一仿真地圖環境下運行。仿真結果表明：當在復雜環境中時，傳統人工勢場法會在第一個陷阱區域或局部極小點的位置停住，無法到達終點；B-APF 算法和C-CPF 算法在陷入陷阱區域后分別通過設立臨時障礙物和虛擬目標點方法幫助機器人逃離陷阱區域和局部極小點，順利到達終點，但是會先陷入陷阱區域，然后再逃離，這樣就導致路徑較長，路徑不夠平滑，多處拐角過大；本文算法通過引入預測距離Rp，在機器人陷入陷阱區域或局部極小點之前做出反應，通過設置合理的虛擬目標點，引導機器人避開陷阱區域，規劃出的路徑較短，而且不存在大的拐角，路徑由幾段直線段組成，路徑平滑。

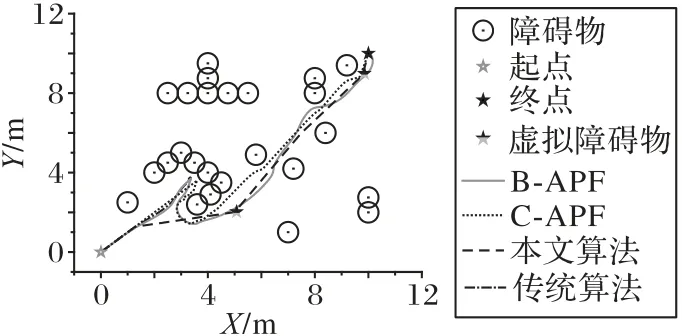
圖7 存在陷阱區域和局部極小點的地圖Fig.7 Map with trap area and local minimum

存在陷阱區域以及局部極小點的仿真數據如表1 所示。由表1 可以看出，傳統人工勢場法無法規劃出完整的路徑；本文算法相較于B-APF 算法，規劃出的路徑縮短了23.08%，算法速度提高了110.96%；本文算法相較于C-APF算法，規劃出的路徑縮短了21.88%，算法速度提高了67.12%。

表1 地圖中存在陷阱區域和局部極小點時的算法數據Tab.1 Algorithm data with trap area and local minimum in map

隨機生成的不存在陷阱區域以及局部極小點的仿真地圖如圖8 所示，幾種算法在同一仿真地圖環境下運行。仿真結果表明：相較傳統人工勢場法、B-APF算法和本文算法，C-APF算法規劃出的路徑存在拐角過大問題，路徑不夠平滑；相較傳統人工勢場法、B-APF 算法和C-APF 算法，本文算法規劃出的路徑略短，且在距離障礙物一定距離的時候提前做出反應，不會存在碰撞危險。

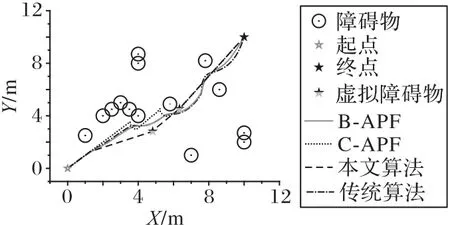
圖8 不存在陷阱區域和局部極小點的地圖Fig.8 Map without trap area and local minimum

不存在陷阱區域以及局部極小點的仿真數據如表2 所示。由表2可以看出，傳統人工勢場法、B-APF算法、C-APF算法規劃出的路徑長短相近，本文算法規劃出的路徑最短；相較于傳統人工勢場法，本文算法規劃出的路徑長度縮短了5.2%，算法速度提高了405.56%。

通過以上仿真結果得到如下結論：當環境地圖復雜，存在陷阱區域以及局部極小點時，本文算法不僅能夠避開陷阱區域和局部極小點，而且路徑平滑簡短；當環境地圖中不存在陷阱區域以及局部極小點時，本文算法規劃出的路徑依舊比傳統人工勢場法簡短；本文算法的運算速度較快。

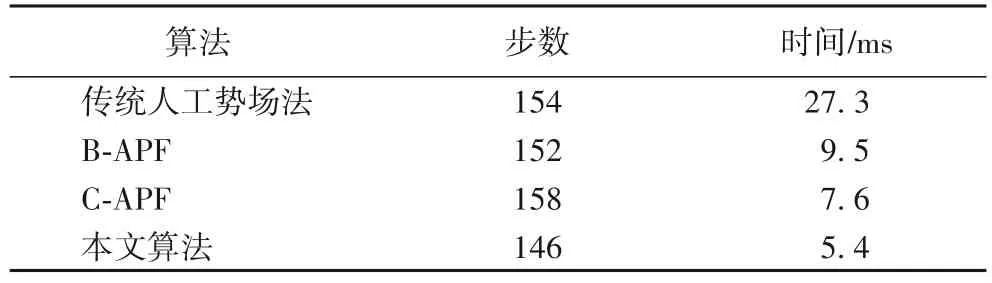
表2 地圖中不存在陷阱區域和局部極小點時算法數據Tab.2 Algorithm data without trap area and local minimum in map

4 結語

傳統人工勢場法在路徑規劃過程中容易陷入陷阱區域，容易在局部極小點附近停止或震蕩，在障礙物環境復雜的情況下無法規劃出完整的路徑。本文通過引入安全距離，對斥力的生成條件和大小進行了改進，消除了無關障礙物對機器人的斥力作用；引入預測距離和虛擬目標點，在機器人陷入局部極小點或者陷阱區域之前，提前改變方向，設置虛擬目標點，引導機器人避開陷阱區域和局部極小點。仿真結果表明，存在陷阱區域和局部極小點的環境下，本文算法可以有效解決傳統人工勢場法路徑規劃中斷問題，順利達到終點；且相較近年來提出的B-APF算法和C-APF算法也有進一步的改進效果。相較于B-APF 算法，本文算法規劃出的路徑長度縮短了23.08%，算法速度提高了110.96%；相較于C-APF 算法，本文算法規劃出的路徑長度縮短了21.88%，算法速度提高了67.12%。不存在陷阱區域和局部極小點的環境下，相較于傳統人工勢場法，本文算法規劃出的路徑長度縮短了5.2%，算法速度提高了405.56%。下一步將考慮在現有環境中隨機加入動態障礙物，進一步提高路徑規劃的難度和真實性。