引入Sierpinski層級特性的新型薄壁多胞管軸向沖擊吸能特性*

何 強，王勇輝，史肖娜，顧 航，陳 宇

（1.江蘇科技大學機械工程學院，江蘇鎮江212003；2.江蘇理工學院機械工程學院，江蘇常州213001）

薄壁結構質量輕并且具有較好的能量吸收特性，常被用來生產各種能量吸收或緩沖裝置，已被廣泛應用于航天航空、車輛工程及國防裝備等領域。薄壁結構在軸向沖擊載荷作用下通過胞壁的塑性變形吸收大量的沖擊能量，所以研究薄壁結構的軸向壓縮特性具有重要的工程意義。

McFarland[1]最先提出正六邊形多胞結構軸向準靜態平均壓縮應力的計算方法，Wierzbicki[2]修正了McFarland 提出的基本折疊模式，并根據超折疊單元理論[3]對正六邊形多胞結構的軸向平均壓縮應力和折疊波長進行了理論求解；Tran 等[4]通過理論和數值手段獲得了多種薄壁管在沖擊載荷作用下的軸向壓縮應力理論模型；尹漢鋒等[5]基于超折疊單元理論對幾種胞元構型蜂窩的平均壓縮應力進行求解，并開展耐撞性優化設計。

薄壁結構的幾何構型對其軸向沖擊載荷作用下的吸能特性有著較大的影響。為提高普通構型（三角形、正六邊形、圓形、正方形等）薄壁管的吸能能力，許多學者對一些新型層級薄壁結構產生了興趣。Sun 等[6]將規則六邊形多胞結構的每個頂點替換為一個較小的六邊形結構，并分析了其軸向沖擊載荷作用下的耐撞性能。Mousanezhad 等[7]提出了具有高剛度和高韌性的蜘蛛網層級多胞結構，并研究了結構參數對其面內及面外力學性能的影響。Sun 等[8]用同性子結構替換了規則六邊形多胞結構的實心胞壁，研究發現該層級特性的引入能大幅度提高其面內剛度。張越等[9]運用數值模擬方法研究了二階自相似四邊形蜂窩結構參數對其面外動態壓縮性能的影響。于國際等[10]研究了二階層級六邊形蜂窩的面內動態壓縮性能。賴燕輝等[11]基于多級蜂窩構型法分析了層級蜂窩的彈性模量等力學參數。

受Sierpinski三角形的啟發，本文中將Sierpinski分形特性引入薄壁吸能管的層級設計，從而提出一種具有Sierpinski層級特性的新型薄壁多胞管(Sierpinski hierarchical tube,SHT)，并對SHTs在軸向沖擊作用下的變形模式和吸能特性進行數值模擬分析。進一步基于能量守恒原理對SHTs在軸向壓縮下的平均壓縮應力理論模型進行求解，以期為新型薄壁構型軸向緩沖吸能裝置的設計提供指導。

1 SHTs的層級結構設計

分形結構可以通過多種方法產生，Sierpinski[12]于1916年提出了一個典型的自相似集，并命名為Sierpinski 三角形。如圖1所示，Sierpinski 墊是一個由若干個三角形構成的自相似幾何結構。

基于Sierpinski[12]的研究工作，本文研究的具有Sierpinski 層級特性的多胞管是通過胞壁連接規則三角形薄壁管胞壁中點形成的。在每個SHT中有3i個邊長為li的單位三角形，通過重復這一迭代過程能夠得到更高階的SHTs，i表示層級數，同時普通三角形薄壁管可以定義為零階SHTs。第零～三階SHTs的結構示意圖如圖1所示。

圖1 SHT幾何結構Fig.1 Geometrical structuresof SHTs

構成SHTs的單位三角形薄壁長度隨著層級參數i的增大而變短，這就會給數值模擬帶來很大的麻煩，因此本文中只考慮到三階SHTs。本文中l0為90 mm，多胞管軸向長度h為250 mm。考慮3組壁厚，即t0=1.0，1.3，1.6 mm，薄壁管的相對密度分別為0.077、0.100和0.123。

由于Sierpinski層級結構特征的引入，本文中所研究的SHTs結構變得更復雜。然而，SHT 作為一種典型的薄壁結構，其仍可以被劃分為若干個典型單元。如圖2所示，所有的SHTs均可看作由2種基本單元組成，即V 形角單元和K 形角單元。

圖2 SHTs結構角單元示意圖Fig.2 Schematic angle elements of SHTs

2 SHTs的軸向壓縮模擬分析

圖3 SHT 軸向壓縮有限元模型Fig.3 A finite element model for dynamic axial compression of an SHT

2.1 SHTs軸向壓縮有限元模型

利用通用顯式非線性有限元分析軟件LSDYNA 模擬軸向沖擊載荷作用下SHTs的動態壓縮特性，計算模型如圖3所示。構建上下端面剛性板，當頂端剛性板沿軸向以10 m/s的恒定速度沖擊薄壁試件時，底端剛性板固定。為了準確地模擬薄壁管的大變形，胞壁采用Beltschko-Tsay 四邊形殼單元，單元厚度方向采用五點積分，面內采用單點積分。基體材料為鋁合金AA6060T4，材料的楊氏模量EY=68.2 GPa，屈服應力σy=80 MPa，極限應力σu=173 MPa，密度ρs=2 700 kg/m3，泊松比μ =0.3，冪指強化因數n=0.23[13]。由于鋁合金對應變率不敏感，本文中未考慮應變率的影響。薄壁管胞壁采用自動單面接觸算法來考慮自身變形產生的接觸；薄壁管與剛性板之間采用自動點-面接觸算法。數值模型中的靜摩擦因數及動摩擦因數均取0.2。

2.2 有限元模型驗證

為驗證該模型的可靠性，首先對薄壁方形管[14]的壓縮行為進行模擬。通過有限元計算后處理可以提取沖擊端應力應變曲線，名義應力σ可表示為：

表1 薄壁方形管動態平均壓縮力模擬結果與實驗數據[14]的比較Table 1 Comparison between simulated and experimental mean dynamic compressiveforces[14]for thin-walled square tubes

模擬結果與實驗數據[14]的比較見表1，誤差均小于10%，表明模擬結果與實驗結果吻合較好。

2.3 變形模式和塑性機理

圖4給出了 ρ ˉ=0.077的不同SHTs結構在軸向沖擊載荷作用下不同時刻的典型變形圖。由于多胞管的底部被固定，胞壁均從沖擊端開始發生塑性變形，隨著沖擊端的不斷下壓，胞元逐層發生折疊變形。研究結果還表明，具有Sierpinski 層級特性的多胞管在軸向壓縮過程中均呈現出軸對稱漸進屈曲模式。軸對稱漸進屈曲是理想的屈曲模式，已有研究表明薄壁結構在受到軸向沖擊載荷作用時也多發生軸對稱的向外屈曲變形[2-5]，并且塑性變形主要集中在管壁的連接處。

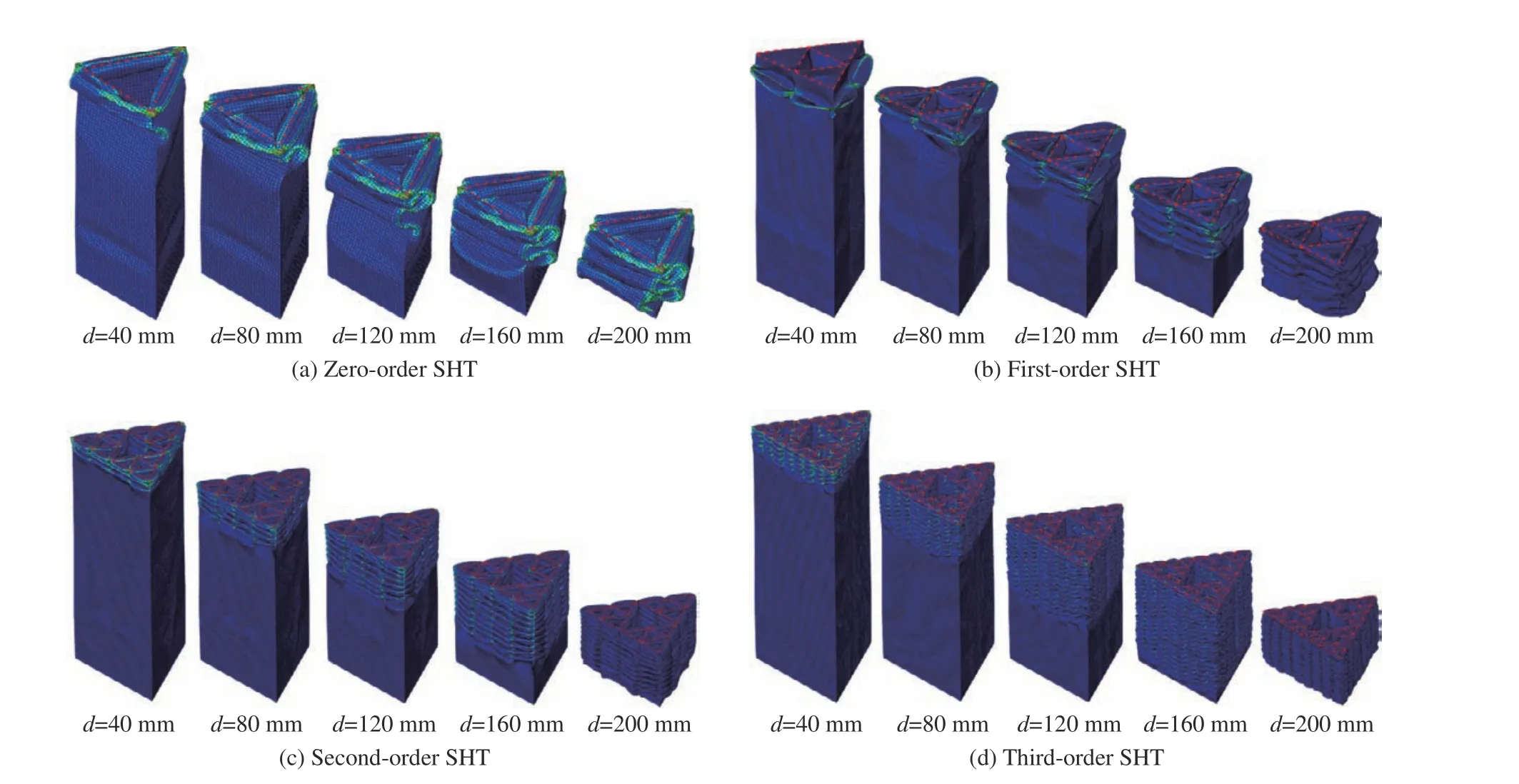
圖4 不同SHTs 的軸向壓縮變形Fig.4 Deformation of different SHTs under axial dynamic crushing

與此同時，Sierpinski 層級特征的引入導致胞元節點段數的增加。為保持結構的相對密度不變，胞壁厚度會變小，從而在某種程度上削弱了薄壁結構的彎曲變形能。與規則三角形管相比，引入Sierpinski 分級特性的多胞管變形吸能最顯著的區別就是折疊單元的數量。SHTs完全折疊單元的數量會隨著層級數的增加而增加。Sierpinski 分級特性的引入大大縮短了胞壁變形的半折疊波長，這也就意味著在壓縮過程中更多的塑性變形能被耗散，增強了薄壁結構的抗壓縮能力。

Abramowicz 等[15]指出，薄壁管在塑性變形過程中有2類基本的變形單元，即非延展性基本單元和延展性基本單元，如圖5所示。圖5中2H為折疊單元高度，圖5(a)中延展吸能區域陰影面積為S*，圖5(b)中延展吸能區域陰影面積為S#。

圖5 兩類基本單元Fig.5 Two kinds of basic elements

前文介紹SHTs結構時提及到作為一種典型的薄壁結構，其仍可以被劃分為若干個典型單元，即如圖2所示，所有的SHTs均可看作由2種基本單元組成，即V 形角單元和K 形角單元。

圖6給出了2種角單元的典型變形輪廓圖，通過對變形模式的仔細觀察能得到SHT 結構在整個變形過程中的2種典型變形模式。這些變形模式主要取決于相鄰胞壁的相對運動。對于V 形角單元，在每一個折疊單元變形過程中，2個胞壁都向同一方向移動，其變形輪廓如圖6（a）所示，這屬于傳統的非延展性變形模式（Ⅰ型）。

對于K 形單元，4個胞壁在折疊變形過程中均向外移動，如圖6（b）所示，此時相鄰胞壁間的變形機理屬于延展性變形模式（Ⅱ型）。

圖6 SHTs變形機理Fig.6 Folding mechanisms of SHTs

3 SHTs的軸向壓縮應力計算

圖7為薄壁結構的胞壁受軸向沖擊載荷作用時的變形示意圖，其中H被稱為胞元折疊單元半波長塑性鉸長度，δ為軸向壓縮長度，q為沖擊載荷。

軸對稱漸進屈曲是理想的屈曲模式，已有研究[2-5]表明薄壁結構在受到軸向沖擊載荷作用時也多發生軸對稱漸進屈曲變形。學者們基于簡化超折疊單元（simplified super folded element,SSFE）理論求解了大量該變形模式下薄壁管的塑性坍塌問題[3-5]。

圖7 薄壁結構在軸向沖擊載荷下的變形示意圖Fig.7 Schematic of thebuckling of a thin-walled structure under axial impact load

SHTs是一種典型的薄壁結構，通過數值模擬和分析可知其在壓縮載荷作用下發生軸向漸進屈曲模式變形，這就啟發我們運用SSFE理論來推導SHTs的軸向壓縮力。為確定SHTs的軸向壓縮應力，還需作如下假設：

(1)薄壁管材料塑性好，可視為理想剛塑性材料；

(2)如圖7所示，薄壁管在軸向壓縮載荷作用下發生向外的軸對稱漸進屈曲，變形過程中各個折疊的塑性鉸長度相等，為2H；

(3)在變形過程中，同一胞元上下表面保持平行，即胞元的各邊變形量相同；

(4)壓縮過程中胞壁間粘接強度足夠大，不發生破裂，可忽略粘接對薄壁結構力學性能的影響。

3.1 SHTs的彎曲耗能計算

圖8 基本折疊單元凸緣充分壓縮示意圖Fig.8 Schematic full compression of a basic folding element flange

3.2 角單元的拉伸耗散能

3.2.1 V 形角單元

圖6給出了簡化超折疊單元理論中的基本

折疊單元延展吸能示意圖，本文中考慮了SSFE理論中的2種拉伸變形模式。圖5(a)所示為變形模式，延展吸能區由3個三角形陰影部分組成，通過對陰影面積積分可求得該變形模式下單個胞壁的拉伸耗散能：

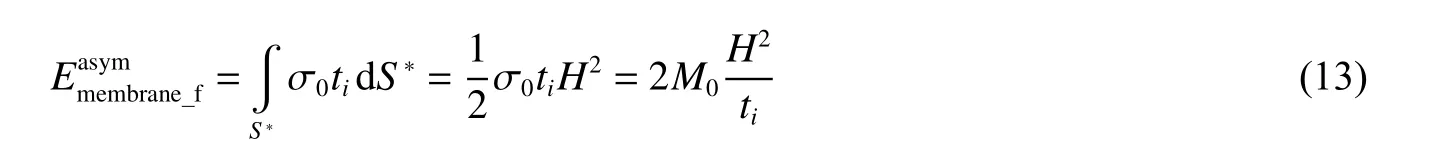
Chen 等[16]指出2個互相連接的胞壁對角單元的拉伸形變能具有相似的貢獻。因此，在非延展變形的情況下，直角單元的拉伸耗散吸能可表示為單個角折疊單元拉伸耗散吸能的2倍：

Tran 等[4]在角單元的拉伸耗散吸能方面做了大量的研究，指出與直角單元相比，V 形角單元的拉伸耗散吸能較小。如圖9所示，V 形角單元在完全塑性坍塌過程中的拉伸耗散吸能可表示為：

圖9 直角角單元與V 形角單元之間薄膜耗散能關系Fig.9 Membrane energy relationship between the rectangular angleelement and the V-angle element

3.2.2 K 形角單元

通過對變形輪廓圖的分析，不難發現K 形角單元的變形機理比直角角單元的變形機理復雜。將K 形角單元的薄膜耗散吸能簡化為由一個V 形角單元和兩個附加平面的薄膜耗散吸能組成。K 形角單元中的每個胞壁都具有相似的變形模式。K 形角單元中包含的V 形角單元與單個V 形角單元具有相同的抗壓強度，需注意的是根據仿真結果（圖7）可知此時的V 形角單元處于延展性變形模式，如圖6（b）所示。陰影部分為延展吸能區，通過積分陰影區域來評估完全塌陷期間每個胞壁的薄膜耗散吸能：

圖10給出了在K 形角單元的拐角處形成的延展吸能三角形單元。K 形角單元中包含的V 形角單元的薄膜耗散能可表示為：

圖10 變形模式Fig.10 Deformation modes

3.3 SHTs的動態平均壓縮應力計算

普通三角形薄壁管，即零階SHTs是由3個V 形角單元組合而成。將式（12）和（15）代入式（9），平均壓縮力Pm,0th的理論計算方程可寫為：

3.4 理論模型模擬驗證

本文中t0分別取1.0、1.3和1.6 mm，胞壁長l0取90 mm，分別對這些新型SHT多胞結構進行軸向壓縮的數值模擬。

用式(29)～(32)計算出動態壓縮應力的理論值，并將其與模擬結果進行比較，如表2所示，當t0=1.0mm（ ρ ˉ=0.077）時，一階、二階及三階SHTs的動態壓縮應力較普通三角形薄壁管分別升高了85.8%、138.2%和183.8%。這表明：將Sierpinski 層級特性應用到薄壁管的設計中，可以有效提高薄壁管的吸能特性。4種薄壁管的動態壓縮應力模擬值和理論值的差異分別為-2.64%～3.42%、-5.23%～1.54%、-2.77%～3.14%和-1.19%～3.67%，結果基本吻合，進一步驗證了本文動態壓縮應力理論推導方法的可行性，說明理論計算結果具有工程應用價值，可用于指導新型薄壁結構軸向緩沖吸能裝置的設計。

4 結論

將Sierpinski分形結構引入到薄壁吸能管的層級設計中，提出了一種具有Sierpinski 層級特性的新型薄壁多胞管（SHT），并通過數值模擬和理論方法研究其受軸向沖擊載荷作用下的變形模式和能量吸收特性，研究結果表明：

（1）具有Sierpinski層級特性的SHTs在軸向壓縮過程中均呈現出理想的軸對稱漸進屈曲模式。SHTs完全折疊單元的數量會隨著層級數的增加而增加。Sierpinski 分級特性的引入大大縮短了胞壁變形的半折疊波長，壓縮過程中更多的塑性變形能量被耗散，增強了薄壁結構的抗壓縮能力。

（2）SHTs均可看作由兩種基本單元組成，即V 形角單元和K 形角單元。V 形角單元在每一個折疊單元變形過程中，兩個胞壁都向同一方向移動，屬于傳統的非延展性變形模式（Ⅰ型）。K 形角單元4個胞壁在折疊變形過程中均向外移動，相鄰胞壁間的變形機理屬于延展性變形模式（Ⅱ型）。

（3）基于能量守恒理論和塑性鉸理論建立了SHTs的塑性屈曲理論模型，獲得了壓潰過程中的塑性彎曲耗散能、薄膜耗散能、軸向壓縮應力的理論表達式，模擬結果與理論計算結果基本吻合，驗證了本文中動態壓縮應力理論推導方法是可行的，理論計算結果具有工程應用價值。

（4）在相同的相對密度下，一階、二階及三階SHTs的動態壓縮應力較普通三角形薄壁管分別增高了85.8%、138.2%和183.8%。將Sierpinski 層級特性引入到薄壁管的設計中，能夠有效提高薄壁管的耐撞性能，這可為新型吸能元件的研究和設計提供參考。