基于改進變分模態分解的電纜局部放電去噪研究

滕本科，彭彥軍，周澤民，趙小林

（廣西電網有限責任公司桂林供電局，廣西 桂林 541000）

0 引 言

電力系統是關鍵的社會基礎設施，對國民經濟的發展與人們生活水平的提高起著重要作用。局部放電檢測作為一種非破壞性技術，已被廣泛應用于評估中高壓電力電纜的絕緣狀態。進行現場局部放電測量時，干擾信號不可避免，嚴重時可淹沒脈沖。因此，如何有效發現電纜的局部放電，及時檢測出潛在的電纜故障，是電力運行單位關心的問題[1,2]。

目前，已有許多去噪方法在局部放電領域使用，但大部分是對特定噪聲設計的，如白噪或窄帶干擾。常見的去噪方法有傅里葉變換、小波變換、經驗模態分解以及奇異值分解等[3]。其中，小波變換在局部信號白噪聲處理方面應用較多，傅里葉變換在局部放電信號窄帶噪聲處理方面應用較多。例如，文獻[4]對小波去噪做了深入研究，文獻[5]將雙樹復小波進入局部放電信號去噪領域，并與傳統小波去噪做了對比，表明該方法優于傳統的小波去噪方法。然而，局部放電信號具有多樣性，去噪時很難選擇完全適合局放信號的小波基、分解層數以及小波閾值等參數，導致在背景噪聲較大時去噪效果一般。與小波變換相比，經驗模態分解和奇異值分解屬于無參數信號分析工具，因此大量學者將這兩種方法引入了局部放電信號領域。例如：文獻[6]提出了一種基于雙變量EMD的局部放電去噪方法，在局部放電去噪中表現出了優于小波變換的性能；文獻[7]采用EMD對超聲波局放信號去噪，取得了較好的效果；還有一些改進的EMD等也得到了大量研究。但是，EMD本質存在的問題都沒得到解決，如誤差累積、在處理多分量強非線性信號時會出現模態混合以及端點效應等。另外，奇異值分解（Singular Value Decomposition，SVD）也是一種使用較多的去噪方法。為了解決SVD分解效率問題，文獻[8]提出了一種自適應SVD分解去噪方法，可以自動選擇和去除與白噪聲相關的奇異值（SV）。文獻[9]提出了一種短時奇異值分解去噪方法，并與自適應SVD進行了比對，結果表明其優于自適應SVD法。但是，該方法當原始信號中含有多個成分時，很難區分除白噪以外的成分。2014年，Dragomiretskiy等提出了變分模態分解法，由于其相較小波變換、EMD分解具有較強的優越性，許多學者很快將其應用于各個領域，如機械學、生物學以及地質學等。文獻[10]實現了VMD模態數的自適應確定，通過互信息判定迭代終止條件，經多次迭代，結合Teager非線性能量算子，提取各IMF的時頻特征。仿真結果表明，VMD能夠有效分解非線性信號，根據互信息確定模態數，以得到的較高的各IMF信噪比。其中，模態數K是影響VMD去噪效果的關鍵因素[4-10]。

為了在去噪的同時保持較好的信號特征，本文將改進的VMD與奇異譜相結合，對采集的電纜局部放電信號進行噪聲處理。首先，基于雙閾值法確定模態數，并對信號進行變分模態分解得到帶限本征模態；其次，使用峭度準則得到有效的帶限本征模態函數；最后，對有效本征模態進行奇異譜去噪，并利用這些去噪的帶限本征模態合成最終的去噪信號。為了驗證去噪方法的有效性和性能，分別從模擬數據和現場試驗中收集局部放電數據進行去噪分析。實例分析證明，該方法具有有效性和優越性。

1 算法原理

1.1 變分模態分解

變分模態分解（Variational Mode Decomposition，VMD）算法最早是由Dragomiretskiy K等人于2014年提出的，是一種基于Wiener濾波的新型信號處理方式。算法針對非平穩和非線性信號具有較好的處理效果。VMD是通過迭代搜尋變分模型最優解來確定模態μk(t)及其對應的中心頻率ωk和帶寬。每個模態都是具有中心頻率的有限帶寬。所有模態之和為源信號。在VMD中，模態被定義為k個有限帶寬的調幅調頻信號，可被表示為：

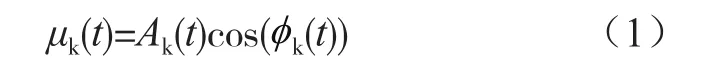
式中，Ak(t)是μk(t)的瞬時幅值；φk(t)是瞬時相位。VMD算法主要包括變分模型構造和模型求解兩個步驟[10]。

1.2 模態數確定方法

從VMD基本原理可知，對于VMD分解結果影響較大的兩個因素是模態數K和懲罰因子α，而模態數K值對分解結果影響最大。K值過大會降低VMD分解效率，且給信號混入更多的背景噪聲和虛假分量，而K值過小會減少有用信號特征。互信息可以表征信號之間的相關度，信息熵可以表征信號的不確定程度，因此本文選取互信息閾值與信息熵閾值來確定最優模態數K。流程如圖1所示。第一，初始化最大模態數K、δλ、n、hλ。第二，n=n+1開始循環。第三，VMD分解得到模態uk(k=1,…,K)。第四，計算模態uk互信息系數δk和信息熵系hk。第五，對得到的δk和hk以降序方式排序。第六，對排序后的數據分別與閾值δλ和hλ進行比較，若其中之一符合條件則終止迭代，得到新的模態數K'。

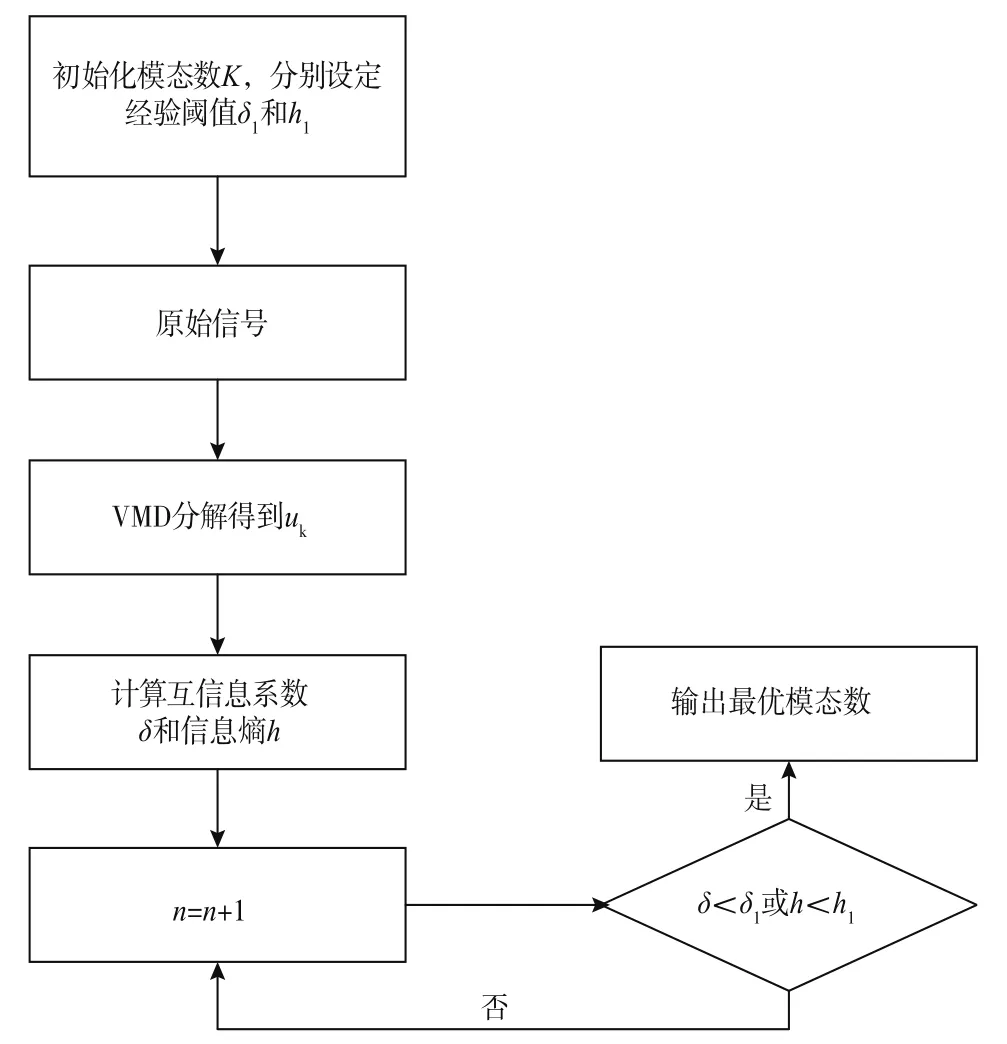
圖1 模態數確定流程

1.3 有效模態數選取

時域上，局部放電信號表現為阻尼振蕩型，而白噪聲與窄帶周期干擾并無此特性，因此VMD算法將信號分解為K個模態量，每個模態量只包含一個有源分量。然而，并不是所有這些模態量成分都有局部放電成分。電纜局部放電信號在時域上有陡峭的上升沿，因此選擇對峰值敏感的峭度作為篩選有效模態的方法。判斷準則為ku(uk)＞ε1，30 kHz＜f0(uk)＜300 MHz。其中，ε1為預設閾值，f0為uk的中心頻率，ku為峭度因子，計算方式為：

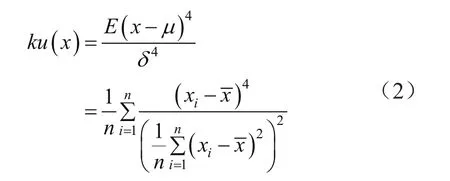
式中，x為信號幅值；為信號的平均值。

1.4 奇異譜閾值去噪法

對選取的有效模態使用奇異譜閾值去噪。首先，對所分解的每個模態進行奇異譜分解。假設分解后特征值按降序排列為λ1≥λ2≥…≥λR≥0，每個特征值的貢獻表示為qi=λi/∑λ（i=1,2,…,R），R為Hankel矩陣秩。計算q的累積和，當r個q的和大于預先設定的閾值時，找到特征矩陣A最佳子空間[11]，基于找出的最佳子空間進行信號重構，并對重構的信號進一步使用小波閾值選取方法進行噪聲處理，則每個模態去噪后的對應信號為Xi。去噪閾值和閾值處理函數分別為：

面對老齡化問題，國家提出了構建“以居家為基礎、社區為依托、機構為支撐”的社會養老服務體系，同時發布了一系列的政策文件，希望能吸納社會閑散資金，拓寬渠道進行養老機構的開發建設。

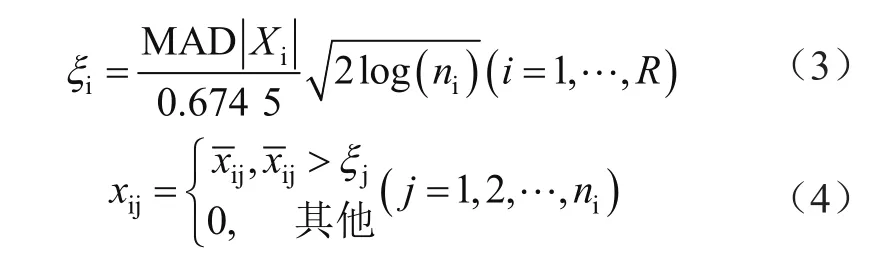
式中，ni為Xi的長度；ζi為閾值。奇異譜閾值去噪法具體流程如圖2所示。

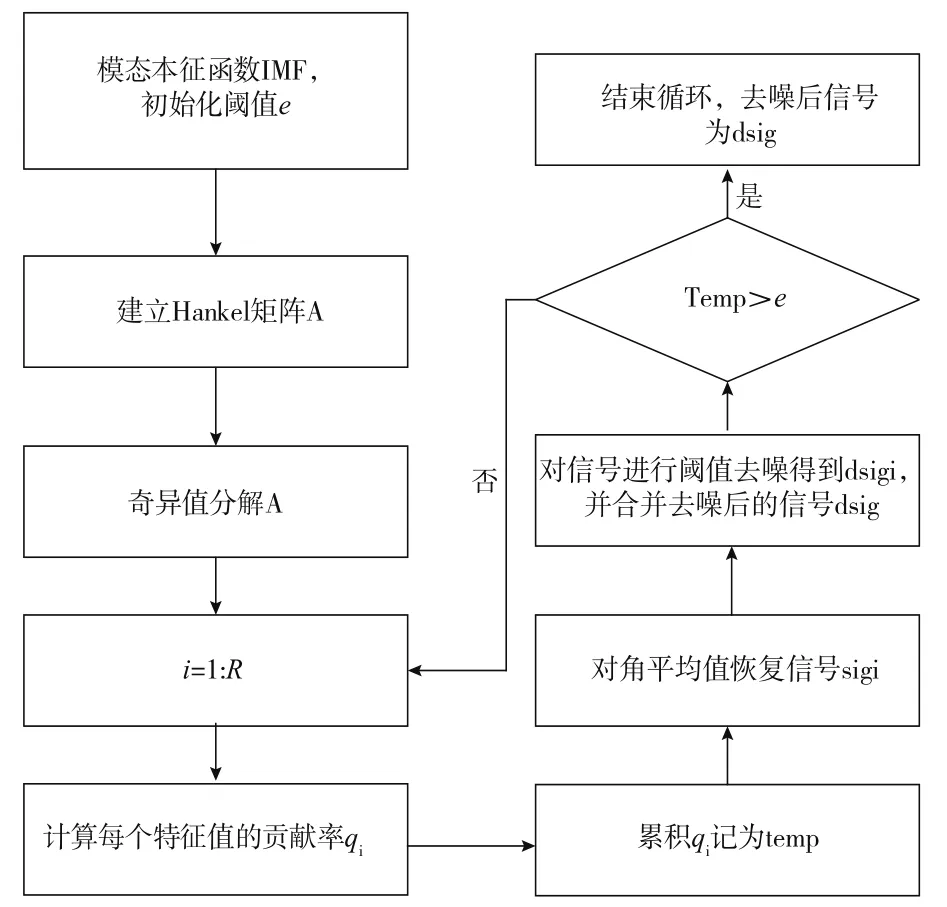
圖2 奇異譜去噪流程圖

2 仿真分析

2.1 模擬信號降噪

為了模擬局部放電信號，選擇1個諧波頻率調制1個指數衰減信號x(k)，將多個x(k)組合仿真周期脈沖局部放電信號，信號的表達式為：

式中，采樣點數為4 096；采樣頻率fs=50 MHz；a為衰減系數；t為采樣時間寬度；k為采樣點數；rand(k)為隨機高斯白噪聲。得到仿真信號加噪前后的時域波形，如圖3和圖4所示，圖4的波形信噪比為-3 dB。根據本文方法對該信號進行降噪，去噪后波形如圖5所示。

2.2 模擬信號降噪效果評價

為了更直觀地比較上述3種方法去噪效果的差異，引入信噪比、均方根誤差、互相關系數以及局部互相關系數4種去噪質量評價方法分別對其進行定量分析。

圖3 原始信號

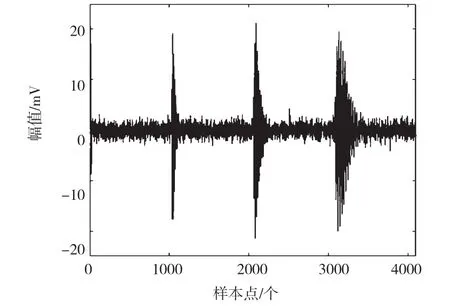
圖4 加噪后的信號

圖5 本文方法去噪后信號

信噪比表示測量信號與噪聲信號功率的比值，一般比值越高，代表降噪效果越好，計算方式為：

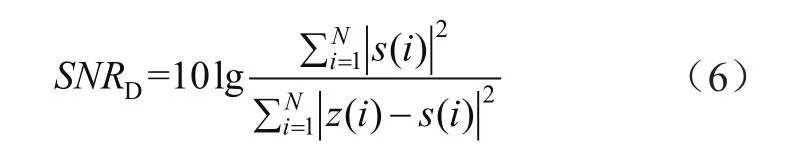
式中，s(i)為原始信號；z(i)為去噪后的信號。

均方根誤差表征原始信號和降噪后信號之間的差異。通常，均方根誤差越小，表示去噪效果越好。它的計算方式為：

互相關系數表征原始信號和降噪后信號的相似度，計算方式為：

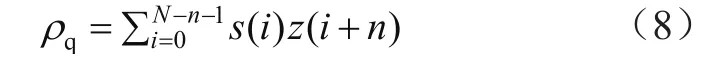
式中，s(i)為原始信號；z(i)為去噪后的信號。

局部互相關系數表征原始放電脈沖與降噪后放電脈沖的相似度。它的計算方式為：

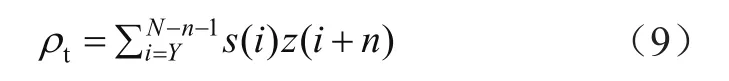
式中，Y為放電脈沖的起始點；z為放電脈沖的終止點。

表1為利用上述4種評價指標分別采用變分模態分解法、奇異閾值法以及本文方法進行去噪的計算結果。可以看出，在信噪比較高時（SNR=10 dB），3種方法的去噪效果均很好，其中采用本文方法的濾波效果最好，其次是變分模態分解法，奇異閾值法效果最差。本文結合了變分模態和奇異閾值方法，去噪后降低了整個波形的畸變程度，放電脈沖部分的相似度最高，接近于1。在信噪比較低時（SNR=-10 dB），3種方法體現出了明顯的去噪差異。其中，奇異閾值法的降噪表現相對較差，本文方法的波形畸變程度最小，濾波效果最好，去噪效果最佳，SNR和SNRD分別表示去噪前的信噪比和去噪后的信噪比。

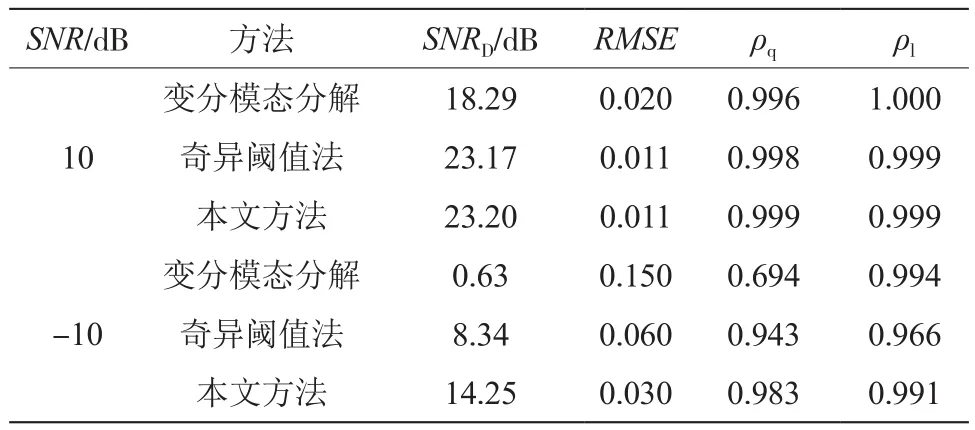
表1 不同去噪方法下的評價參數

3 現場實測數據處理

為了驗證上述方法處理實際復雜數據的能力，本文在10 kV電纜上進行局部放電檢測試驗。圖6（a）為在某個試驗電壓下，一個工頻周期內懸浮缺陷引起的局放脈沖波形幅值-時間序列，右上角的細節圖為第一個脈沖的局部放大圖。圖6（b）、圖6（c）以及圖6（d）分別是采用變分模態分解法、奇異閾值法以及本文方法對上述波形進行處理后的結果。

從圖6可以看出，采集到的懸浮缺陷放電脈沖信噪比較高，3種方法的去除噪聲干擾的能力均很強。因此，當采集到的放電波形信噪比較高時，3種方法均可作為局放去噪方法。

圖7（a）為在某個試驗電壓下，一個工頻周期內尖端缺陷引起的局放脈沖波形幅值-時間序列，右上角的細節圖為第519 μs脈沖的局部放大圖。圖7（b）、圖7（c）和圖7（d）分別是采用變分模態分解法、奇異閾值法和本文方法對上述波形進行處理后的結果。

圖6 不同算法下懸浮缺陷放電波形去噪圖

從圖7可以看出，尖端缺陷引起的放電脈沖具有較低的信噪比，經奇異閾值法去噪后的波形與原始波形近乎一致，但還有一些噪聲殘留。變分模態分解法去除了所有的噪聲干擾，但從右上角的局部放大圖可以看出，幅值較小的脈沖也會被濾除。相比于上述兩種方法，本文方法去除噪聲干擾能力強且造成的波形失真較小，效果最佳。

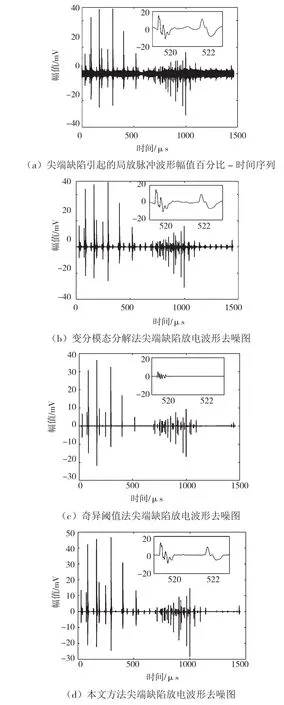
圖7 不同算法下尖端缺陷放電波形去噪圖

4 結 論

本文基于已有的局部放電去噪研究，提出了一種改進變分模態分解方法來抑制電纜局部放電檢測時包含的噪聲，并對不同噪聲強度下不同類型的局部放電信號進行評估。與變分模態分解法和奇異閾值法相比，本文方法能夠更有效地濾除噪聲干擾，且降噪后的信號更接近原始信號，同時信噪比、均方根誤差以及互相關系數3個性能指標表現更好。通過仿真分析和實測數據的結果可以看出，本文方法降噪效果更好，同時證明了降噪能力與局放信號類型和噪聲水平均無關系。