基于慣性測量的管道彎頭角度與走向解算方法

楊理踐，郭方智，高松巍，劉 斌，李佳音，靳 鵬

(沈陽工業大學 信息科學與工程學院，沈陽 110870)

管道廣泛應用于油氣產品的輸送中，進行管道檢測并實現管道完整性管理極其重要。管道彎頭是管道埋地分布中必然存在的管道結構之一，管道彎頭的曲率半徑等參數又影響著管道的通過能力，是實現管道完整性管理必要的基礎數據。楊金生等[1]通過計算內檢測器的行進速度與通過彎頭時的角速度的比值，得到曲率半徑。慣性導航技術應用于管道內檢測方面的研究多針對慣性導航系統中的慣性測量單元存在漂移的問題，圍繞減小隨距離和時間累積而增大的位置誤差進行[2-3]。武漢大學以實際管線測量為例，利用里程計與非完整性約束等輔助信息抑制誤差累積，并采用平滑算法進一步提高測量精度[4-5]。靳鵬等[6]利用檢測器在發球筒中初始姿態可控、可測的特點，設計了迭代Kalman(卡爾曼)算法及終止迭代的判斷方法，提高了初始對準及后續管道地理坐標的解算精度。

筆者利用慣性測量單元和里程計的輸出信息，建立管道彎頭解算模型并推導彎頭角度和彎頭走向，獲得角度、曲率半徑和走向等管道彎頭參數，為管道完整性管理提供了參考依據。

1 檢測原理

1.1 慣性導航測量原理

管道內檢測器以輸送介質的壓力差為動力，在管道內部沿管道中心線運動，對管道的腐蝕、裂紋等缺陷及管道的幾何變形等進行在線檢測。管道漏磁內檢測器結構如圖1所示。

圖1 管道漏磁內檢測器結構示意

搭載在管道漏磁內檢測器上的慣性導航系統以慣性測量單元(inertial measurement unit，IMU)為主，實時采集載體的運動姿態信息。通過將測量數據、管道外校驗點和里程計數據結合，并進行解算，實現管道地理坐標的測量。

1.2 檢測器坐標系統與歐拉角

慣性導航系統以一定頻率采集IMU和里程計數據，并保存在存儲系統中。IMU主要包含有三軸陀螺儀和三軸加速度計，用于測量檢測器的角速度和加速度信息。陀螺儀和加速度計的坐標系統保持一致，y軸正方向為檢測器前進方向，檢測器坐標系統如圖2所示。

圖2 檢測器坐標系統示意

ωx,ωy,ωz為陀螺儀繞x,y,z軸旋轉時測得的角速度，方向垂直于轉動平面，通過右手螺旋定則確定；Ax,Ay,Az為加速度計沿坐標軸測得的加速度，沿坐標軸正方向輸出為正；vodo1,vodo2,vodo3為三路里程計沿檢測器前進方向行進的速度。

通過引入歐拉角，描述檢測器相對于地面的姿態：俯仰角θ的定義域為[-90°,+90°]，上仰為正；橫滾角γ的定義域為[-180°,+180°]，右傾為正；航向角ψ的定義域為[0°,360°]，北偏東為正。角速度，即單位時間內繞旋轉軸旋轉方向上的角度變化量。結合歐拉角的定義，對陀螺儀的三軸角速度ωx,ωy和ωz分別進行積分得到角位移，積分結果依次對應俯仰角θ，橫滾角γ和航向角ψ。

2 管道彎頭角度與走向解算方法

2.1 解算模型

管道彎頭角度與走向解算主要包括數據輸入、數據預處理、彎頭參數解算和結果輸出等4個部分。原理框圖如圖3所示。

圖3 管道彎頭角度與走向解算原理框圖

其中，數據預處理包括原始數據濾波處理、補償陀螺儀零偏誤差、里程計算等。

管道彎頭參數輸出包含起始處里程、彎曲段中心線弧長、彎頭角度、曲率半徑、曲率和彎頭走向等6項。

管道彎頭各特征參數如圖4所示。管道彎頭特征為管道中心線曲率發生變化的彎曲段，其兩端與直管段相連。圖中，D為管道公稱直徑；起始處里程和管道彎曲段中心線弧長為ΔS，可由里程計數據計算得到；Δη為管道彎頭角度；R為曲率半徑，一般以管道公稱直徑D為單位。

圖4 管道彎頭各特征參數示意

曲率半徑為

R=ΔS/(Δη)

(1)

曲率半徑R的倒數即為管道曲率K

K=1/R

(2)

曲率用來表示該處管道的彎曲程度，曲率越大，管道的彎曲程度越大。

2.2 管道彎頭角度解算方法

對管道彎頭段的三軸陀螺儀輸出角速度分別積分得到角位移后，根據角度合成算法，合成得到管道彎頭角度。對陀螺儀數據進行積分得到俯仰角θ，橫滾角γ和航向角ψ

(3)

式中：ωx,ωy,ωz分別為陀螺儀繞x,y,z軸旋轉時測得的角速度。

搭載在檢測器上的IMU通過管道彎頭的過程為載體坐標系不斷旋轉的動態過程，任意選取該動態過程中某一時刻下載體坐標系構成的三維空間，建立三維空間角度合成模型。

(1) 三維空間角度合成模型

建立三維空間下的角度合成模型(見圖5)。

圖5 三維空間角度合成模型

圖中，空間直角坐標系為O-xyz，P為x-O-y平面中非x軸上的一點，線段OP長為a；過P點向x軸做垂線，垂足為F，線段OF長為b，∠POF為α；過點P做x-O-y平面的垂線段HP使∠POH為β，線段OH長為c；∠HOF為ζ。

在直角三角形OPF、OHP中，存在關系：

cosα=b/a

(4)

cosβ=a/c

(5)

經數學推導可知，在直角三角形OHF中，存在

cosξ=b/c

(6)

結合式(4),(5),(6)，可得

cosξ=(b/a)(a/c)=cosαcosβ

(7)

ξ=arccos(cosαcosβ)

(8)

式(7),(8)完成了在三維空間下對兩個垂直平面x-O-y和P-O-H中角度分量α和β的合成。

(2) 管道彎頭角度合成算法

將檢測器通過管道彎頭時的姿態變化分解成3個部分,分別為繞x軸旋轉θ，繞y軸旋轉γ和繞z軸旋轉ψ。結合管道檢測的特點分析，檢測器在管道中運動時受到約束，即其在沿管道中心線單向前進時，繞前進軸(y軸)旋轉得到的橫滾角γ對于管道彎頭角度的大小沒有貢獻。所以在計算合成管道彎頭角度時，只考慮繞非前進軸(x軸和z軸)旋轉得到的俯仰角θ和航向角ψ。管道彎頭角度合成如圖6所示。

圖6 管道彎頭角度合成示意

圖6中，坐標系O-xyz依次經過繞z軸旋轉ψ、繞X軸旋轉θ后得到O-x′y′z′和O-x″y″z″，A′和A″由x-O-y平面內的一點A依次經兩次旋轉得到。

由于陀螺儀三軸相互正交，式(7),(8)適用于檢測器通過管道彎頭時整個動態過程的角度合成，可推得

cos Δη=cosθcosψ

(9)

Δη=arccos(cosθcosψ)

(10)

式中:Δη即為計算得到的管道彎頭角度，結合里程計數據可計算該段的曲率半徑和曲率。

2.3 管道彎頭走向解算方法

結合檢測器沿管道中心線單向前進的運動特性，得到描述彎頭走向的八種結果，為正左、正右、正上、正下、左上、左下、右上和右下。載體縱軸(y軸)指向大地平面的上方為上，反之為下；載體縱軸(y軸)在大地平面上的投影指向彎頭起始處管道中心線的左側為左，反之為右。從彎頭起始處沿管道中心線看去，彎頭走向如圖7所示。

圖7 管道彎頭走向示意

利用IMU的三軸加速度計數據，可計算重力加速度g并解算檢測器在管道彎頭起始處的姿態。

(1) 彎頭起始處姿態信息

由于彎頭起始處的航向角ψ0僅作為航向基準，可任意給定，所以只需要計算彎頭起始處的橫滾角γ0和俯仰角θ0以提供彎頭走向解算的初始姿態信息。

檢測器姿態解算模型如圖8所示。載體坐標系為O-xyz，重力加速度g被沿x,y,z軸分解，重力大小分別為Ax,Ay和Az。

圖8 檢測器姿態解算模型

重力加速度大小g與三軸分量存在關系

(11)

沿平行于大地平面且垂直于檢測器的方向看去[見圖8(b)],在重力加速度g與y軸構成的平面下，俯仰角θ與重力分量間存在關系：

(12)

沿檢測器行進方向，即從y軸正方向看去[見圖8(c)]。在x-O-z平面下，橫滾角γ與重力分量間存在關系

(13)

(14)

檢測器在實際行進過程中，因輸送介質的持續推動，難以獲取檢測器位于彎頭起始處靜止狀態下的加速度計數據。由于進入彎頭前檢測器位于直管段且管線走向保持不變，可選取直管段各軸加速度計數據完成彎頭起始處姿態信息的解算。

(2) 彎頭終止處姿態信息與彎頭走向

(15)

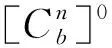
(16)

將式(16)寫成T矩陣的形式

(17)

由式(16),(17)可得

(18)

經過n次計算完成整個管道彎頭段姿態的更新，將整個過程表示為經過1次姿態更新得到

(19)

終止處的俯仰角θ、橫滾角γ、航向角ψ可由式(17)對應的T矩陣計算得到。

由此得到了檢測器在彎頭起始處和終止處姿態信息的解算方法，通過計算彎頭終止處相對起始處檢測器的姿態偏轉，實現管道彎頭走向的提取。

3 試驗與結果分析

3.1 試驗平臺

搭載有MPU6500姿態傳感器的檢測器完成各項調試后，從試驗管道入口進入，試驗過程中關閉盲板并確保管道氣密性良好。打開注水加壓閥加壓，皮碗前后介質的壓力差推動檢測器沿管道中心線行進，直至檢測器通過整條試驗管道并到達出口。試驗管道公稱直徑為168 mm，全段包含6個標準45°彎頭，管道總長約為15.6 m。管道試驗模型與試驗平臺結構如圖9,10所示。

圖9 管道試驗模型示意

圖10 試驗平臺結構示意

MPU6500姿態傳感器實時測量檢測器的運動姿態信息，經支持系統采集后與提供里程信息的編碼器輸出信息一同被上位機記錄。

3.2 數據處理

對試驗得到的測量數據進行預處理，數據預處理前后加速度計和陀螺儀的測量數據如圖11所示。

由圖11(a)可知，在預處理前的測量數據中，加速度計和陀螺儀數據均存在異常跳變的現象，需根據其特點對測量數據進行濾波處理；三軸陀螺儀數據的基準角速度非零，因此存在因陀螺儀失調帶來零偏誤差的情況，需對測量數據整體進行誤差補償。

圖11 預處理前后的測量數據對比

由圖11(b)可知，在預處理后的測量數據中，加速度計和陀螺儀數據均無異常跳變的現象，且三軸陀螺儀數據基準角速度均為0，零偏誤差已得到補償。

3.3 試驗結果與誤差分析

利用MATLAB軟件解算管道彎頭參數，管道彎頭參數解算結果如表1所示。

表1 管道彎頭參數解算結果

表中依次給出了6個管道彎頭經解算得到的參數信息。試驗與解算結果表明，該方法可準確解算管道彎頭走向并計算相關參數，角度計算誤差在7%以內。

4 結語

利用IMU及里程計的輸出信息建立了管道彎頭參數解算模型，經解算可得到彎頭角度、曲率半徑、曲率和彎頭走向等參數。該方法能夠滿足工程實踐需求，具有較高的工程實用價值。