基于混合元啟發式算法優化神經網絡的熱舒適度預測模型

朱嬋

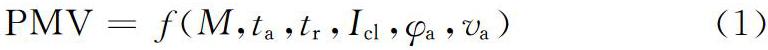
摘 要：熱舒適度指標的計算過程具有多參數、非線性、高復雜度等特點，致使空調的實時控制器無法直接使用。針對這一問題，提出了一種基于混合元啟發式算法神經網絡的熱舒適度預測模型：GACS神經網絡。其中，GACS算法是一類融合了遺傳算法和布谷鳥搜索的混合元啟發式算法。仿真實驗表明：與遺傳算法相比，GACS算法在全局搜索能力方面得到了極大提升，其優化出的GACS神經網絡具有更高的預測精度。

關鍵詞：熱舒適度;PMV指標;神經網絡;遺傳算法;布谷鳥算法

中圖分類號：TP311

文獻標志碼：A

文章編號：1007-757X（2020）11-0066-04

Abstract：The calculation process of thermal comfort index has the characteristics of multi-parameters， non-linearity and high complexity， which makes the real-time controller of air conditioning unable to be used directly. To solve this problem， a thermal comfort prediction model based on hybrid meta-heuristic algorithm and neural network is proposed， i.e.， GACS neural network. GACS is a hybrid meta-heuristic algorithm， it combines genetic algorithm and Cuckoo search. The simulation results show that compared with genetic algorithm， GACS algorithm has greatly improved the global search ability， and the optimized GACS neural network has higher prediction accuracy.

Key words：comfort;PMV index;neural network;genetic algorithm;Cuckoo search

0?引言

目前，大型建筑物內的空調控制方案大多以恒溫控制為主，這不僅無法滿足用戶對熱舒適度的多樣化需求，還導致了不必要的能源消耗。上世紀60年代，丹麥工業大學的Franger教授提出了熱舒適度方程，該方程可根據環境參數和人類活動情況綜合計算出人體的熱舒適度指標（Predicted Mean Vote，PMV指標）[1]。1984年，國際標準化組織（ISO）根據Franger教授的研究成果制訂了ISO7730標準，即《適中的熱環境——PMV與PPD指標的確定及熱舒適條件的確定》[2]。熱舒適度方程表明：人體舒適度與人類活動、衣著、空氣溫度、濕度、風速等多方面因素有關，因此，根據實際場景靈活調整空調的設定，可以在保證舒適度的前提下，有效降低空調能耗[3]。但熱舒適度方程的計算具有多參數、非線性、高復雜度等特點，而空調實時控制器結構簡單，無法完成計算[4]。2002年，高立新、白樺等人提出利用BP神經網絡構建PMV快速預測模型，仿真實驗表明，該模型的預測準確率在95%以上，完全能夠滿足空調實時控制系統的要求[5]。此后，研究者們通過不同途徑優化預測模型，不斷提高預測精度。2010年，徐巍、陳祥光等人提出利用遺傳算法和BP神經網絡相結合的方式優化室內熱舒適控制參數，大幅度提高了算法的預測效率[6];2014年，張玲、王玲等人提出利用改進的粒子群算法優化BP神經網絡的熱舒適度預測模型，該方案改善了對網絡初始值敏感的問題，同時有效提高了預測精度，其預測誤差僅為9×10-4[7];2015年，閆婷在其碩士論文中，提出利用蟻群算法優化BP神經網絡，其預測正確率達到了99.88%[8];

2018年，郭彤穎，陳露等人提出利用鳥群算法優化基于BP神經網絡的熱舒適度預測模型，該模型較粒子群算法在收斂速度和預測精度上均有提升[9]。已有的研究表明，BP神經網絡經過多次訓練可有效提高預測的精度，然而，其預測結果嚴重依賴隨機生成的網絡初始參數。通過遺傳算法優化后的神經網絡在預測穩定性方面大大提高，但遺傳算法本身全局搜索能力的欠缺又導致預測結果容易陷入局部最優[10]。為此，

本文將利用遺傳算法和布谷鳥算法構建混合元啟發式算法優化神經網絡，再利用改進后的網絡建立PMV預測模型，仿真實驗表明該預測模型能準確地預測PMV指標，其最佳預測誤差僅為8.7×10-5。

2?熱舒適度的預測平均投票模型

預測平均投票模型中主要涉及到四個環境因素和兩個人類活動因素，其中環境因素包括空氣溫度ta、平均輻射溫度tr、空氣相對濕度φa和風速va;人類活動因素包括人體新陳代謝率M和服裝熱阻Icl。因此，當人體做功為0時，PMV指標可由式1所示的函數形式表出，具體計算方法在參考文獻[1]中有詳細描述，如式（1）。

PMV指標的計算結果代表了大多數人在環境中的冷熱感受，其取值通常在-3到3之間，整數值的具體含義ISO7730認定熱舒適環境應保證其PMV取值位于-0.5到0.5之間[2]，如表1所示。

3?BP神經網絡與混合元啟發式算法

3.1?BP神經網絡

BP神經網絡全稱為Error Back Propagation Network，即誤差反向傳播網絡，是目前理論體系最為完善、應用最為廣泛的算法模型。其特點是在訓練網絡時，根據輸出結果的誤差，從輸出層開始逐層向前修正權值、閾值以達到降低誤差的目的[11]。本文采用的BP神經網絡為三層結構，如圖1所示。

其中，第一層為輸入層包含6個神經元，分別表示人體新陳代謝率、空氣溫度、平均輻射溫度、服裝熱阻、空氣相對濕度和空氣流速;第二層為隱含層包含16個神經元，訓練函數為logsig（ ）;第三層為輸出層包含1個神經元表示PMV指標， 訓練函數為purelin（ ）。

3.2?GACS算法

GACS（Genetic Algorithm-Cuckoo Search，GACS算法）是一類混合元啟發式算法，目前常見的元啟發式算法有遺傳算法、禁忌搜索、粒子群算法、布谷鳥搜索和蟻群優化算法等。這類算法通常基于一種仿生策略，通過反復迭代搜索找出最優解，但根據策略的不同，算法各有優缺點。因此在算法之間取長補短重新構成出一種尋優能力更強、搜索效率更高的混合算法是目前元啟發式算法研究的重點[12]。本文提出的GACS算法由遺傳算法（Genetic Algorithm，GA）和布谷鳥搜索（Cuckoo Search，CS）混合而成。其中，遺傳算法于上世紀六十年代由美國密歇根大學的 Holland教授提出，算法通過模擬自然界優勝劣汰的進化機制，對隨機生成的解集進行反復迭代搜索，最終找出最優解。由于算法具有高度的并行性且通用性強，因此在各行各業都得到了廣泛應用[13]。布谷鳥搜索由劍橋大學的Xin-She Yang、Suash Deb于2009年提出，該算法模擬了布谷鳥的寄生育雛和Lévy飛行機制，通過長、短距離飛行交替進行的方式，使得算法具備了卓越的全局搜索能力[14]。本文在遺傳算法中加入布谷鳥搜索機制，將改善遺傳算法全局搜索能力較弱，容易陷入早熟的問題，算法流程如圖2所示。

算法的主要步驟如下。

步驟一：利用BP神經網絡生成的初始化種群，其個體由BP網絡的初始權值、閾值構成;

步驟二：將個體所對應的BP神經網絡預測精度作為其個體適應度;

步驟三：依次執行遺傳算法的選擇、交叉、變異操作;

步驟四：選取適應度較低的20%的個體進行布谷鳥搜索;

步驟五：判斷是否滿足遺傳迭代的停止條件，滿足則輸出搜索結果，不滿足則跳轉至第二步。

下面就GACS算法中的幾個重要部分進行詳細闡述。

（1） 初始種群與個體：GACS算法的優化對象為BP神經網絡的權值和閾值，種群中的一個個體對應一種網絡的結構，初始種群由隨機生成的N個BP網絡訓練而來，即種群規模為N。任意個體Xi采用二進制編碼，其長度L=（I×H+O×H+O）×P，其中I、H、O為輸入層、隱含層、輸出層的神經元數量，P為權值和閾值的二進制位數。

（2） 個體適應度：一個個體對應一組BP神經網絡的權值閾值組合即網絡結構，個體適應度等于該網絡預測出的PMV值與實際取值的絕對誤差值，即適應度越低表示該個體越靠近最佳解。

（3） 遺傳操作：在遺傳算法中選擇、交叉、變異操作合稱遺傳操作，每次迭代都會對種群依次執行所有遺傳操作。GACS算法中，遺傳操作為隨機遍歷抽樣，代溝值為0.9;交叉操作為單點交叉，交叉概率為0.7;變異操作為離散變異，變異概率為0.7Lind，其中Lind為個體的長度L。

（4） 布谷鳥搜索：在完成遺傳操作后，按種群規模的20%選取適應度較的個體集合進行布谷鳥搜索，搜索中將依序執行以下三步操作。

步驟一：利用Lévy飛行模擬找尋新巢的過程即產生新的個體集，Lévy飛行[14]的具體操作，如式（2）。

式中，Xt+1為新個體集;Xt為舊個體集;α為飛行步長，通常取值為1;levy（β）為Lévy隨機路徑，β通常取值為1.5。

步驟二：選取新個體集中前10%的優勢個體替換舊個體集中的劣勢個體，從而構建出新的種群。

步驟三：模擬宿主發現寄生行為的過程，以25%的概率pa拋棄種群中的劣勢個體，并隨機生成新個體用以替換，新個體的產生方式[14]，如式（3）。

式中，Xt+1為新個體集;Xt為舊個體集;r、ε為服從均勻分布的隨機數;Heaviside（）為單位階躍函數函數;pa為拋棄概率，取值為0.25;xi、xj為任意個體。

3.3?GACS神經網絡

BP神經網絡具有高度復雜的非線性結構，容易導致內部出現多個局部極值點。同時，網絡訓練結果嚴重依賴系統隨機生成的權值和閾值[11]。為提升網絡的全局搜索能力和預測精度，本文在確定神經網絡的拓撲結構后，利用GACS算法優化神經網絡的權值和閾值，再通過梯度下降法對GACS算法的優化結果進行補充訓練，最終找出預測精度最高的熱舒適度預測模型，GACS神經網絡執行流程，如圖3所示。

GACS神經網絡執行流程如下。

步驟一：確定神經網絡的拓撲結構，如圖1所示;

步驟二：初始化種群，種群由BP神經網絡訓練而來，一個個體代表一種網絡結構;

步驟三：計算個體適應度;

步驟四：執行遺傳操作;

步驟五：執行布谷鳥搜索;

步驟六：判斷是否滿足迭代的停止條件，滿足進入下一步，不滿足跳轉至第三步;

步驟七：利用梯度下降法對種群進行最后一次優化;

步驟八：算法結束，輸出預測結果。

4?仿真實驗及數據分析

為驗證GACS神經網絡的預測精度，本文隨機生成了700組參數組合，并根據Fanger教授的熱舒適度方程計算其PMV指標，其中，600組作為訓練樣本，100組作為測試樣本。相關參數的取值范圍分別是：人體新陳代謝率M為36～200 W/m2、空氣溫度ta為20～35 ℃、平均輻射溫度tr為10～40 ℃、服裝熱阻Icl為0～1clo、空氣相對濕度φa為30～70%、空氣流速va為0～1 m/s。仿真實驗平臺為MATLAB R2015a，通過編程分別實現了基于GA神經網絡和基于GACS神經網絡的熱舒適度預測模型。實驗中，算法種群規模為600，迭代次數為500，兩種網絡的種群均值變化過程如圖4、圖5所示。

最優解的搜索過程如圖6、圖7所示。

圖4和圖5分別展示了GA神經網絡和GACS神經網絡在500次迭代過程中，種群均值的變化過程。GA神經網絡的種群均值在第11代時獲得了3 641的峰值，之后迅速收縮，從第20代起，基本徘徊在2 300以下的區間。GACS神經網絡則在第74代時，種群均值依然達到了3 497的高位取值，并且在250代到400代之間，其均值仍多次接近3 000。可見，GACS神經網絡利用布谷鳥的Lévy飛行機制，在迭代過程中很好的保持了個體多樣性大幅提高了算法的全局搜索能力，有效避免了算法早熟。

圖6和圖7分別展示了GA神經網絡和GACS神經網絡在500次迭代過程中，最優解的搜索過程。GA神經網絡的最優解取值在第51代時降至0.06，第269代時降至0.05，最終在第500代時降至0.048。GACS神經網絡的最優解取值則在初期就得到了較快收斂，在第18代時就降至0.04，第160代時降至0.36，最終在第500代時降至0.35。可見，GACS神經網絡在最優解的搜索過程中，得到了更為精確的預測模型，如圖8所示。

選取了GACS神經網絡預測結果中的100個個體 ，以此為例，展示了基于GACS神經網絡的熱舒適度模型的預測值與實際PMV取值的對比結果。經計算，GACS神經網絡的最佳預測精度達到了8.7×10-5。在該精度下，預測模型可更為精確的預測當前環境的熱舒適度，從而為建筑空調運行提供更為優化的節能運行方案。

5?總結

本文依據Fanger教授提供的熱舒適度方程，提出一類基于混合元啟發式算法的熱舒適度神經網絡預測模型。其中，用于優化神經網絡的混合元啟發式算法為GACS算法，該算法在遺傳迭代中融入了布谷鳥搜索，有效提高了全局搜索能力，其最佳預測精度達到了8.7×10-5。但在研究中還存在諸多不足之處，例如：由于GACS算法添加了布谷鳥搜索，其運行過程中需多次計算個體適應度，導致其搜索速度大大降低;另外，本文中遺傳算法采用的是二進制，而布谷鳥搜索是十進制，使得每次迭代中均需要進行十進制和二進制的相互轉換，進一步影響了整體算法的運行效率。因此，在后續研究中，還需不斷深入研究，在提高GACS神經網絡預測精度的同時，提升其搜索的效率。

參考文獻

[1]?朱穎心. 建筑環境學[M]. 北京：中國建筑工業出版社，2016：94-140.

[2]?ISO. International Standard 7730. Moderate thermal environment-determination of the PMV and PPD indices and specification of the conditions for thermal comfort [S]. Geneva：International Standard Organization， 1984.

[3]?鐘瀟. 基于熱舒適度的建筑空調用電優化研究[D]. 華北電力大學，2016.

[4]?Jian Yao， Jin Xu. Research on the BPNN in the prediction of PMV[J]. Applied Mechanics and Materials，2010，29（32）：2804-2808.

[5]?高立新，白樺. 利用神經網絡預測PMV指標[J]. 北京：哈爾濱建筑大學學報，2002，35（5）：70-72.

[6]?徐巍，陳祥光，彭紅星.基于神經網絡和遺傳算法優化室內熱舒適控制參數[J].北京理工大學學報，2010，30（2）：240-244.

[7]?張玲，王玲，吳桐. 基于改進的粒子群算法優化反向傳播神經網絡的熱舒適度預測模型[J]. 計算機應用，2014，34（3）：775-779.

[8]?閆婷. 基于蟻群與神經網絡算法的變風量空調末端控制研究[D].西安建筑科技大學，2015.

[9]?郭彤穎，陳露.基于鳥群算法優化BP神經網絡的熱舒適度預測[J].計算機系統應用，2018，27（4）：162-166.

[10]?周毅.以熱舒適度為目標的室內空調環境建模、優化與仿真研究[J].自動化應用，2017（12）：13-15.

[11]?陳明. MATLAB神經網絡原理與實例精解[M]. 北京：清華大學出版社，2012：156-191.

[12]?徐俊杰. 元啟發式算法：理論闡釋與應用[D]. 合肥：中國科學技術大學出版社， 2015.

[13]?雷英杰，張善文，李續武，等. MATLAB遺傳算法工具箱及應用[M]. 西安：西安電子科技大學出版社，2005：1-8.

[14]?黃繼達. 布谷鳥算法的改進及其應用研究[D].武漢：華中科技大學，2014.

（收稿日期：2019.08.29）