“同心鼓”顛球最佳策略建模

莫京蘭，伍楊楊，黃羽婷，袁 森

(廣西科技大學鹿山學院，廣西 柳州 545616)

1 問題

素質拓展是培養團隊精神、凝聚團隊合作力的一種戶外活動，該活動中又包含各式各樣的活動項目，其中有一項活動最能體現團隊合作能力——“同心協力”，它是用同樣的心使同樣的力。

題目：一面牛皮雙面鼓，鼓身周圍固定有多根繩子，固定點與繩子皆均勻分布，每個隊員都拉著一根繩子的末端，使鼓面維持水平，將垂直落下的球顛起，按標準的顛起高度作為參考，球顛越多則獲勝。問題1，在團隊每個人能精準控制用力方向、力度和時機的理想狀態下，討論團隊最佳協作策略及顛球高度。問題2，現實中，團隊每個人不可能準確地控制發力時機和用力大小，其中必然會導致鼓面產生傾斜。假設隊員有8人，繩子長1.7 m，鼓面于初始狀態為水平靜止，鼓面的初始位置比繩子水平位置低了0.11 m，據所給數據中隊員的用力大小和發力時機建立數學模型，描述隊員某一時刻的鼓面傾斜角與力度和發力時機的關系，并求出0.1 s時鼓面的傾斜角度。考慮到現實因素帶來的影響，在問題2的模型基礎上，思考是否對問題2的最佳協作策略進行調整。如果鼓面傾斜，球將不再豎直向上跳動，則需要調整隊員的拉升策略。當隊員人數為8人、繩子長2 m、球有60 cm反彈高度、球跳動方向與豎直方向夾角為1°、且跳動的傾斜方向的水平投影指向兩隊員之間、其角度比為1∶2。在可精準控制條件下給出所有隊員的發力時機和力度來將球的跳動方向調整為豎直方向，并分析在現實中此調整策略的可行性與實施效果的任務。

2 模型假設

忽略空氣阻力對實驗造成的誤差影響；忽略球與鼓之間相互撞擊為彈性撞擊，不考慮能量損失；假設鼓和球均完好，不影響使用；不考慮不同用力大小的站位問題；不考慮團隊隊員自身情況所造成影響；不考慮活動經行過程發生的意外因素。

3 問題分析

問題1。在理想狀態下進行條件假設，建立數學模型，尋找團隊合作使顛球數量盡可能多的最佳策略，求出最佳策略下的最佳高度。通過分析題目所給數據，對球運動過程進行分析，判斷該項目球與鼓的運動是否屬于能量守恒問題。以能量守恒為導向，以顛球高度、拉力角度、人對鼓所作力的大小為線索，尋找最適合解決問題的數學模型。

問題2。需要考慮到現實情況。每個人反應的速度、使用的力度有所不同，則發力時機，發力大小有所不同，這導致鼓面發生傾斜，產生傾斜角。從分析不同力度下產生的高度差下手，根據題目所給信息，尋找可行的數學模型，分析角度與時機、力度之間的關系。

問題3。在問題2的數學模型上，考慮實際情況，繩長與角度帶來的影響。又對問題2的數學模型進行優化，重新調整策略。

問題4。需要調整拉繩策略。根據題目假設，在問題2數學模型基礎上，在理想情況下，采用問題1所得最佳用力大小，尋找豎直方向產生傾斜夾角時所產生的高度差，從而得到調整策略。又考慮到現實情況，對調整策略進行分析。

4 模型建立和解決

4.1 問題1模型建立和求解

4.1.1 模型建立

從題目所給條件，根據球的大概運動過程，選擇球與鼓接觸后向上彈起瞬間作局部受力分析，進行建模。在理想狀態下，不考慮空氣阻力，在沒有能量損失的條件下該運動過程中球滿足能量守恒條件。球運動過程中，能量守恒：mgH+W=mgh，假設顛球高度保持在0.4≤h≤1圍內最合理。

根據以上條件可得出人對球做功的約束范圍0≤W≤1.59。

4.1.2 模型求解

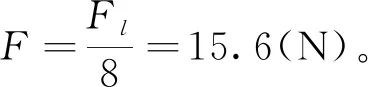
4.1.3 結果分析

從模型求解結果可以分析出每個隊員在理想狀態下的最佳策略，如表1所示：

表1 最佳策略結果分析Tab.1 Analysis of optimal strategy result

從表1可以清楚看出繩長為0.78 m時人對鼓的拉力。拉力屬于合外力分力范圍內，證明假設合理。所以發力時機為球接觸鼓面的瞬間，繩子傾斜角為45°，每個人對鼓使用力大小為15.6 N，此為最佳策略。在該策略下，高度假設合理，考慮到省力、點球次數盡可能多等因素，選取0.6 m為該策略下的最佳高度。

4.2 問題2模型建立和結果分析

當人對鼓施加一個特定的拉力Fi時，會產生一個向上的支持Ti。根據問題2所給數據，對鼓與拉力進行特定受力分析，又因不同的時機、不同的用力大小都會影響鼓抬起的高度，會產生一個高度差，這時建立一個用力大小在時機約束條件下與鼓面傾斜角的關系分析模型。

4.2.1 模型建立

4.2.2 模型求解

從力影響高度、時機影響高度兩方面將1～9組進行粗分。

A.1～3屬于t1時間下，力對高度產生影響。

②當F2=80 N時，支持力的大小為T2=10.353 N，此時所產生加速度大小為a2=13.207 m/s，所抬起的高度為x2=0.066 m，所以8人中有1人用力90 N時，所產生高度差為Δx=x1-x2=0.014 m，此時可得鼓面的傾斜角約為θ1≈1.25°。同理可求得有兩人用力為90 N時，所產生的鼓面傾斜角約為θ2≈2.08°，θ3≈1.89°。

B.4～6屬于Fi=80 N時，時間t1，t2對高度的影響。

①當t1=0.1 s時，所抬起高度為x3=x2=0.066 m。

②當t2=0.2 s時，所抬起高度為x4=0.264 m，因此8人中有1人發力時機屬于t2時，所產生的高度差為Δx=x4-x3=0.198 m，此時鼓面的傾斜角為θ4≈1.06°。同理可求得有兩人時，在時間t2的影響下，產生的鼓面傾斜角θ5≈1.96°，θ6≈1.32°。

C.7～9屬于t2時間下，力影響高度。

①當F1=90 N時，通過A所得求解結果可計算出此時所抬起高度為x5=0.322 m。

②當F2=80 N時，同理計算出抬起高度為x6=0.264 m，因此在t2時間下，一人用力大小為90 N所產生的高度差為Δx=x5-x6=0.058 m，此時鼓面的傾斜角為θ7≈2.35°。同理可得有兩人用力90 N時，繩子的傾斜角為θ8≈1.54°,θ9≈1.08°。

根據求解結果，0.1 s時鼓面傾斜角可歸納為表2：

表2 0.1s時鼓面的傾斜角Tab.2 Slant angle of the drumhead at 0.1s

4.3 問題3模型建立和解決

問題1中可知隊員之間的最小距離不得小于0.6 m，所以繩子不能小于0.78 m。考慮到現實因素，繩子長度在一定限值下，角度過大，鼓會碰到地面。問題2的模型中，可得繩子傾斜角度。

4.3.1 模型優化和求解

4.3.2 模型結果分析

在繩長為0.78 m的情況，以問題2為基礎，調整方案如表3所示。

表3 調整后策略方案Tab.3 Strategy schedule after adjustment

所以調整后策略為發力時機相同，繩子傾斜角調整為10°，每個人對鼓使用65.5 N的力，此時為最佳策略。

4.4 問題4模型建立和解決

若鼓面發生傾斜不處于水平狀態時，致使球彈起運動不屬于豎直上拋，運動方向發生改變，且在反彈時相對于豎直方向產生1°的傾斜。由角度關系證明定理可知，1°的傾斜角相對于平面發生了的1°傾斜。所以，為了將球調整為豎直狀態，則在球類下降過程中，應將鼓面傾斜角1°。

因人數10人，所以人員的站位為正十邊形，且人與人的夾角度數為36°。利用對角線判斷方法，將人員分為兩組，以1～5號為第一組，6～10號為第二組進行受力分析。經研究分析，傾斜方向與位置沒有關系，因此假定傾斜落在8號與9號之間，且在位置上，傾斜位置更偏向于9號。所以，要想改變傾斜角度為水平，必須改變該線上的作用時間或者是力的大小，因此對模型進行限制。

在水平方向上：

設F(i=1，2，3，…，9，10)為繩上拉力，θ為繩子與水平線上的夾角，所以，在水平上的受力為Fi·cosθ，在y軸上，矢量和為0，得F1·cos4°+F2·cos40°+F3·cos76°+F5·cos36°=0。

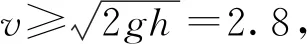
因為在理想狀態下，問題1中最大合外力為Fl=124.73 N，利用問題2所得模型，求得在10人情況下，使用力度合外力為Fl=124.73 N，每個人提供加速度a3=34.647 m/s，調整時間為t3=0.020 1 s。

根據受力時間條件下t3取0.1 s作為計算，調整鼓面傾斜度時加速度a4=13.8 m/s2，調整拉力為p=5.026 N，調整后用力大小為F=20.63 N。

由此得出調整后的策略方案，如表4所示：

表4 調整后策略結果Tab.4 Strategy results after adjustment

根據表4結果可知，在現實情況中，人不可能在球發生傾斜后能準確地控制調整時間、調整力度，但調整策略結果與整數調整相差不大，實施效果良好。

5 結語

“同心鼓”這項運動中，理想狀態下沒有能量損失，利用排球掉落彈起過程的受力分析，尋找出顛球高度、拉力角度、人對鼓所作力的大小之間的關系，同時考慮到實際彈起高度，建立最佳策略模型。在特定用力大小下的受力情況，從不同用力對高度影響、不同時機與高度影響兩個大方面考慮鼓面因為高度的不同所產生的傾斜角。通過物理計算，建立了用力大小、發力時機與傾斜角的關系模型。現實情況下，人不可能準確地把握時機、力度，因此調整策略效果不能達到理想效果，通過分析調整策略效果，使得模型屬于合理范圍內。