毫米波大規模MIMO 系統中的一種低復雜度的混合波束賦形方案*

周 圍，彭 洋，冉靜萱，陳星宇，馬茂瓊

（1.重慶郵電大學，重慶 400065；2.重慶郵電大學移動通信技術重慶市重點實驗室，重慶 400065）

0 引言

為解決現如今數據流量急劇增加、頻譜資源緊缺等問題，第五代移動通信系統（Fifth Generation，5G）結合了毫米波和大規模多輸入多輸出（Multiple Input Multiple Output，MIMO）技術。一方面，毫米波可以提供更大的頻帶寬度，解決頻譜資源緊缺的問題；另一方面，雖然毫米波在信道中傳輸存在較高路徑損耗的問題，但毫米波的短波長特性可以減小系統中的天線尺寸，便于集成更多的天線，可結合大規模MIMO 技術克服傳輸路徑損耗，提升通信速率。

波束賦形（Beamforming）是使電磁波在特定方向傳輸的技術。傳統MIMO 系統中的純數字波束賦形算法，要求每個陣元配置一條射頻（Radio Frequency，RF）鏈。但是，在大規模MIMO 系統中，若每個陣元仍配置一條RF 鏈，將會造成高昂的成本和巨大的能耗。目前，研究人員為減少使用RF 鏈，多采用模擬/數字的混合波束賦形的架構，即模擬域只采用簡單的移相器構成高維的模擬波束賦形器，而數字域采用低維的數字波束賦形器。

近年來，混合波束賦形技術因其低成本、低能耗的特點逐漸受到研究者的廣泛關注。文獻[1]提出基于稀疏空間的S-OMP 算法，核心思想是最小化混合波束賦形矩陣和純數字波束賦形矩陣之間的歐式距離。但是，S-OMP 算法需要次循環獲得模擬波束賦形矩陣FABF，且每次循環都會對FABF進行求逆運算獲得數字波束賦形矩陣FDBF[2]。文獻[3]通過對HHH進行SVD 分解得到右奇異矢量，將其歸一化得到模擬波束賦形矢量FABF，后通過得到的FABF和已知的最優數字波束賦形矩陣得到低維的FDBF。文獻[4]提出Beam Steering 算法，是一種結合碼本和信道估計的模擬波束賦形算法，但要在天線陣列趨于無窮才能達到最佳性能[2]。文獻[5]基于毫米波相控陣架構提出了一種迭代波束成形方法，收發端進行迭代發送和接收信號，找到毫米波信道中具有最大增益的路徑，但文獻[5]僅僅針對單用戶場景并未討論存在干擾用戶場景。

針對以上傳統的混合波束賦形方案需要進行信道估計和高維信道矩陣的SVD 分解等問題，本文在毫米波大規模MIMO 系統中設計了一種低復雜度的混合波束賦形方案，通過結合波束掃描和自適應算法避免了信道估計、SVD 分解等問題。由于自適應算法可將主波束對準期望用戶和零陷對準干擾用戶，因此可以獲得良好的信干噪比和頻譜效率性能。

1 系統模型

設大規模MIMO 基站（Base Station，BS）端服務于K個用戶，BS 處設置M個接收天線。

1.1 陣列模型

智能天線屬于陣列天線，由多個相同的全向天線組成。陣列結構可以有多種形式，常見的有均勻直線陣（Uniform Linear Array，ULA）、平面陣以及均勻圓陣（Uniform Circular Array，UCA）等，如圖1 所示。

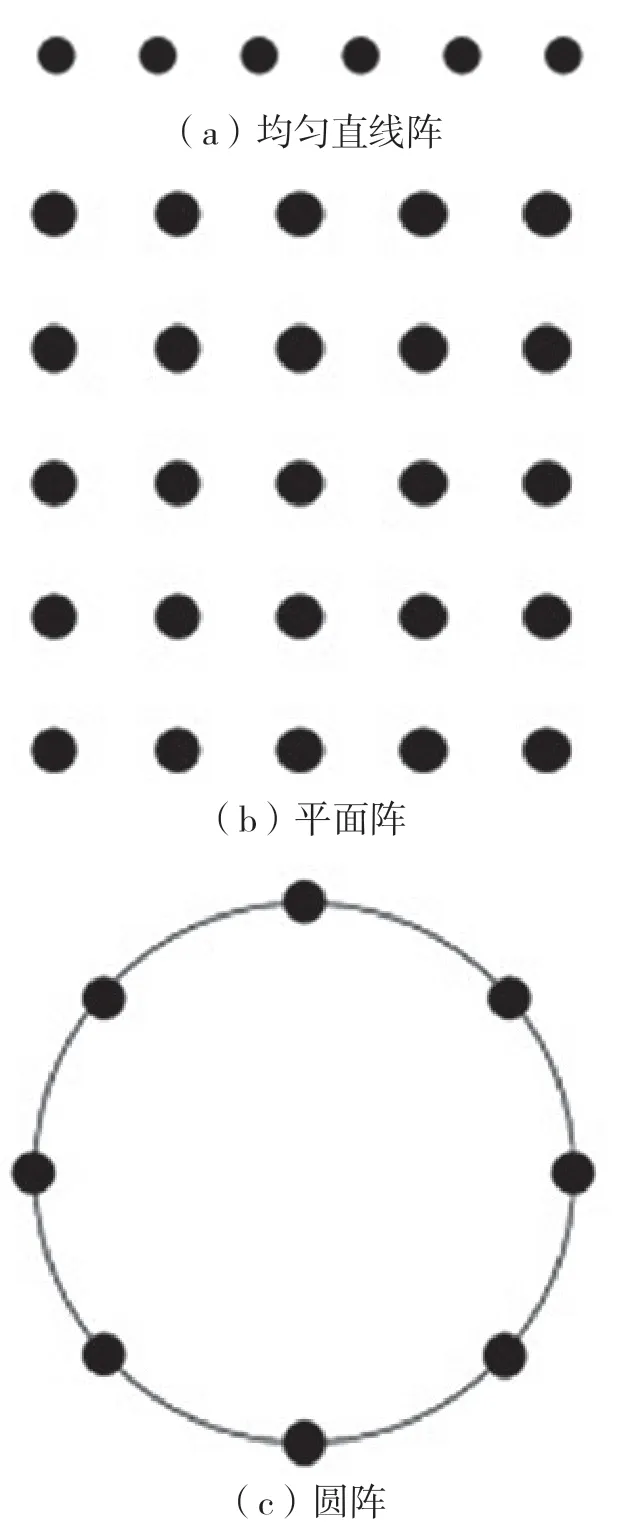
圖1 陣列結構

本文采用均勻直線陣，陣列響應表達式如下：

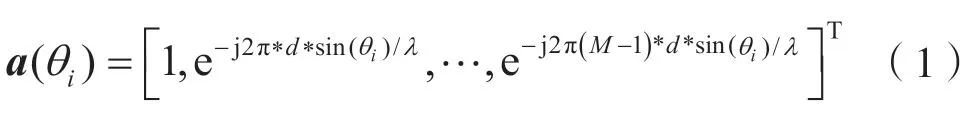
式中，M為天線陣元數量，d為陣元間距，λ為波長，θi(i=1,2,…,K)為方位角。

陣列接收信號模型如下：

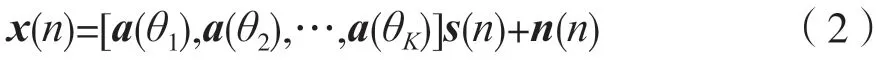
式中，x(n)=[x1(n),x2(n),…,xM(n)]T為陣列接收信號矢量；s(n)=[s1(n),s2(n),…,sK(n)]T為信號矢量；θ1為期望用戶方向；θ2,θ3,…,θK為干擾用戶方向；n(n)=[n1(n),n2(n),…,nM(n)]T，其中ni(n)(i=1,2,…,M) 為第i個陣元上的加性高斯白噪聲。

1.2 陣列連接方式

傳統的純數字波束賦形技術需要較多的RF鏈，將造成系統成本高昂和巨大的能耗等問題。因此，在大規模MIMO 系統中采用混合波束賦形技術成為可行思路。混合波束賦形器按照RF 鏈與天線的連接方式，可分為全連接型和部分連接型兩種結構，如圖2 所示。

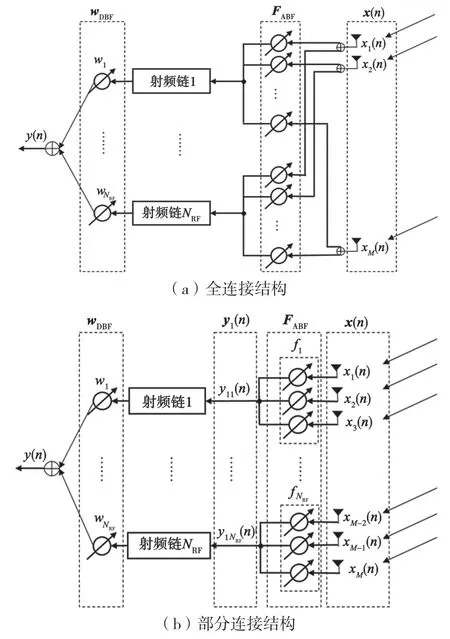
圖2 連接模式

在全連接型結構中，RF 鏈通過移相器與全部陣元連接，可以有效利用大規模天線陣列的陣列增益。但是，這種連接方式十分復雜，需用到MNRF個移相器，導致系統的能耗增加。在部分連接型結構中，天線陣列被分成若干個子陣列。一條RF 鏈通過移相器僅與一個子陣列中的所有陣元相連接，連接方式簡單，使得系統所需的移相器大大減少，有效降低了系統能耗。

由于部分連接型結構連接簡單且能耗低，因此具有較強的實際應用價值。本文將重點研究部分連接型結構。完成陣列結構的選擇后，陣列的輸出表達式如下：

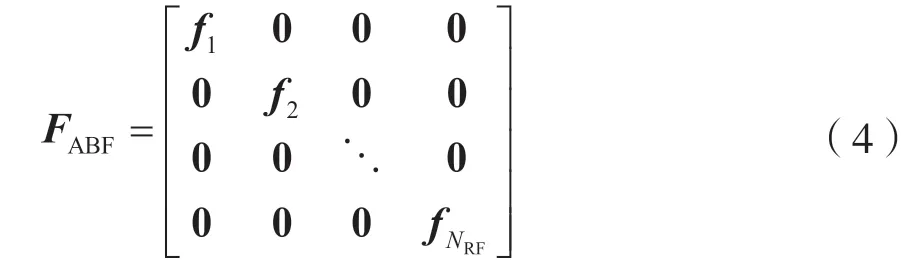
式中，NRF為射頻鏈數量，fi∈，i=1:NRF，Msub=M/NRF為子陣數量。

2 提出方案

本文設計了一種結合波束掃描和自適應算法的低復雜度混合波束賦形方案，方案分為兩個階段，其中自適應算法選擇LMS 算法進行分析。

2.1 基于期望信號的波束掃描

在S-OMP 算法中，雖然涉及到碼本的設計，但波束是根據與最優數字波束賦形矩陣的殘差來選擇的。碼本設計采用DFT 碼本[6]，得到碼本波束矩陣為：

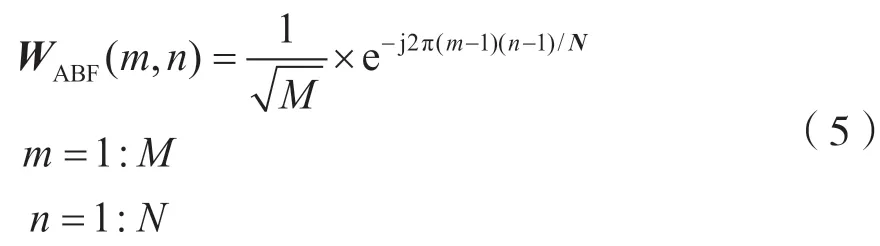
式中，N為波束數。

本文為避免S-OMP 算法中的模擬波束賦形涉及信道估計的問題，結合文獻[5]只采用一條射頻鏈的思路，提出了一種波束掃描方法，即陣列接收信號通過一條射頻鏈輸出到數字域進行迭代搜索，搜索出使得輸出信號與期望用戶信號的幅度差值最小所對應的波束作為模擬波束賦形矩陣。

本方案具體流程如下。

（1）初始化：誤差功率E1=0；快拍數L=512

（2）開始迭代搜索：

（3）找出I1×L中出現次數最多的數值imax

（4）最優波束權矢量為fABF=WABF(:,imax)

由于本文采用部分連接型架構，則式（4）中的矢量fi,i=1:NRF表示如下：

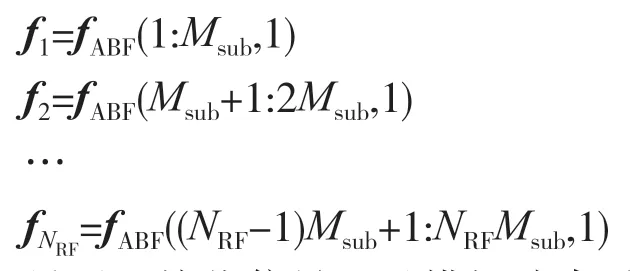
最后，接收信號通過模擬波束賦形后得到的第一級輸出：

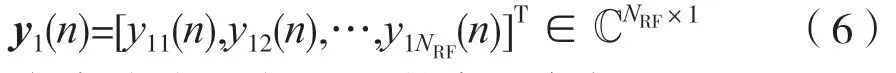
由式（5）可得y1(n)的表達式為：

2.2 LMS 自適應算法

通過2.1 節提出的波束掃描方法，可以得到碼本中最接近期望用戶方向的波束。本文結合數字域的自適應算法進一步優化波束，可以使主波束對準期望用戶方向，同時將零陷對準干擾用戶方向，且自適應算法仍然不涉及信道估計、高維矩陣求逆等操作。

本文采用LMS 自適應算法[7]，通過第一級輸出y1(n)和期望用戶信號s1(n)獲得低維的數字波束賦形矢量wDBF，算法如下。

（1）初始化：wDBF=0；L=512

（2）進行迭代：

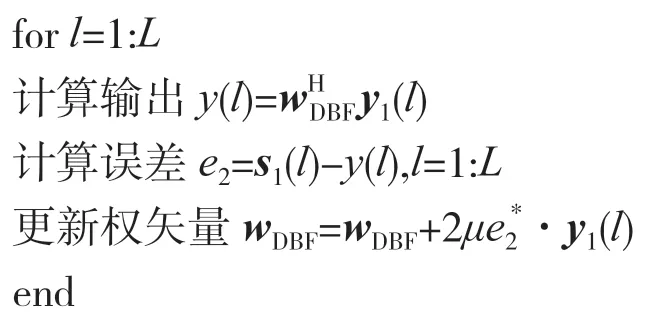
（3）得到最優權矢量wDBF

2.3 信干噪比和頻譜效率

本文方案主要通過信干噪比（Signal to Interference plus Noise Ratio，SINR）和頻譜效率（Spectral Efficiency，SE）等性能進行評價。混合波束賦形后，輸出信號中期望用戶功率為：

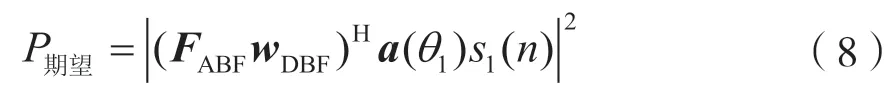
輸出信號中干擾用戶功率為：

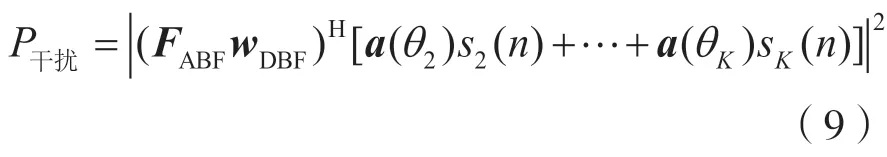
輸出信號中噪聲功率為：

由式（8）～式（10）可以得到信干噪比：

根據信干噪比，可以得到頻譜效率表達式為：

3 仿真結果分析

為了驗證所設計混合波束賦形方案的性能，本文分別從信干噪比、頻譜效率以及誤碼率等性能對其進行仿真分析，同時與僅采用波束掃描和純數字波束賦形進行比較，仿真條件如表1 所示。

表1 仿真條件

實驗采用蒙特卡羅的仿真方法，曲線中每一個值都是1000 次仿真的平均值。

3.1 碼本設計仿真

本文采用DFT 碼本，波束數量設置為4，根據式（5）設計碼本波束，仿真結果如圖3 所示。

3.2 波束掃描仿真

在得到設計的碼本后，通過本文設計的波束掃描方案得到最接近期望用戶方向的碼本波束，如圖4 所示。

3.3 誤差收斂分析

實驗中，令步長μ=0.0001。第一級輸出作為LMS 自適應算法的輸入，算法執行完成后可以通過圖5 觀察算法執行過程中誤差的收斂情況。圖5 表明，隨著信噪比（Signal to Noise Ratio，SNR）的增大，誤差收斂加快；在SNR=20 dB 時，迭代50 次即可達到收斂。

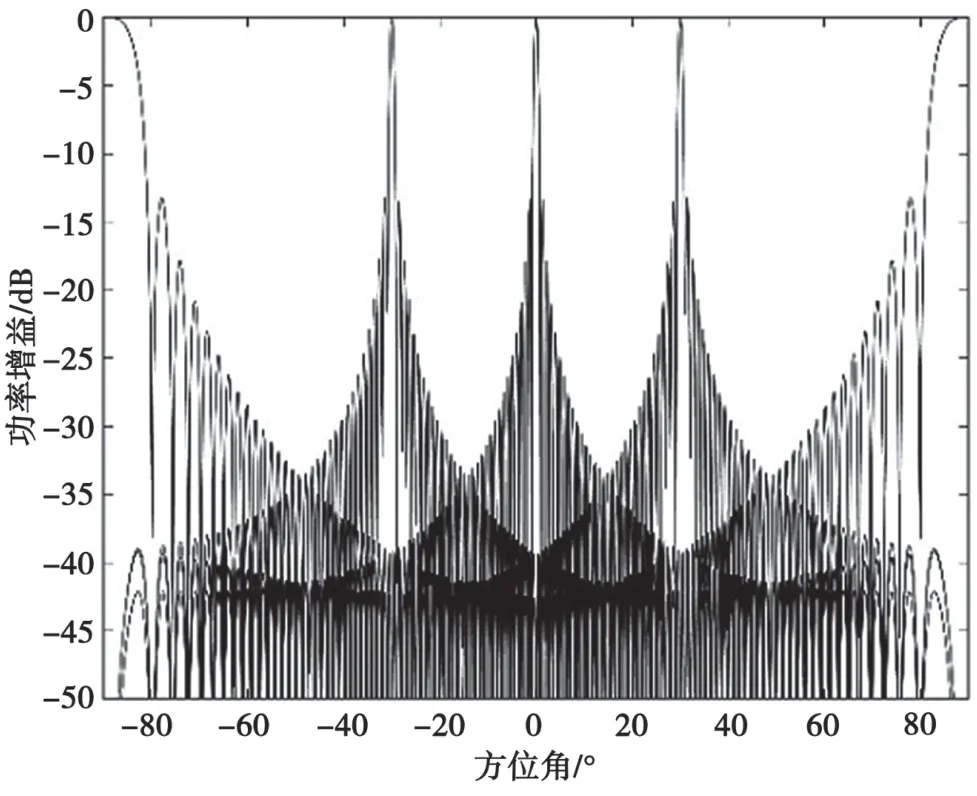
圖3 碼本波束仿真結果

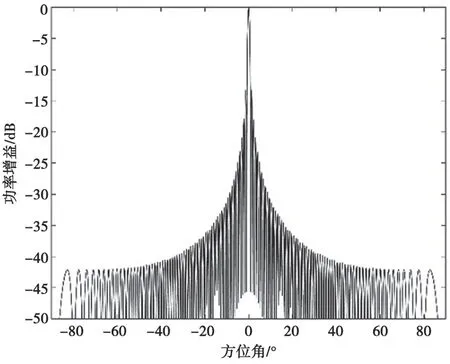
圖4 模擬波束賦形波束

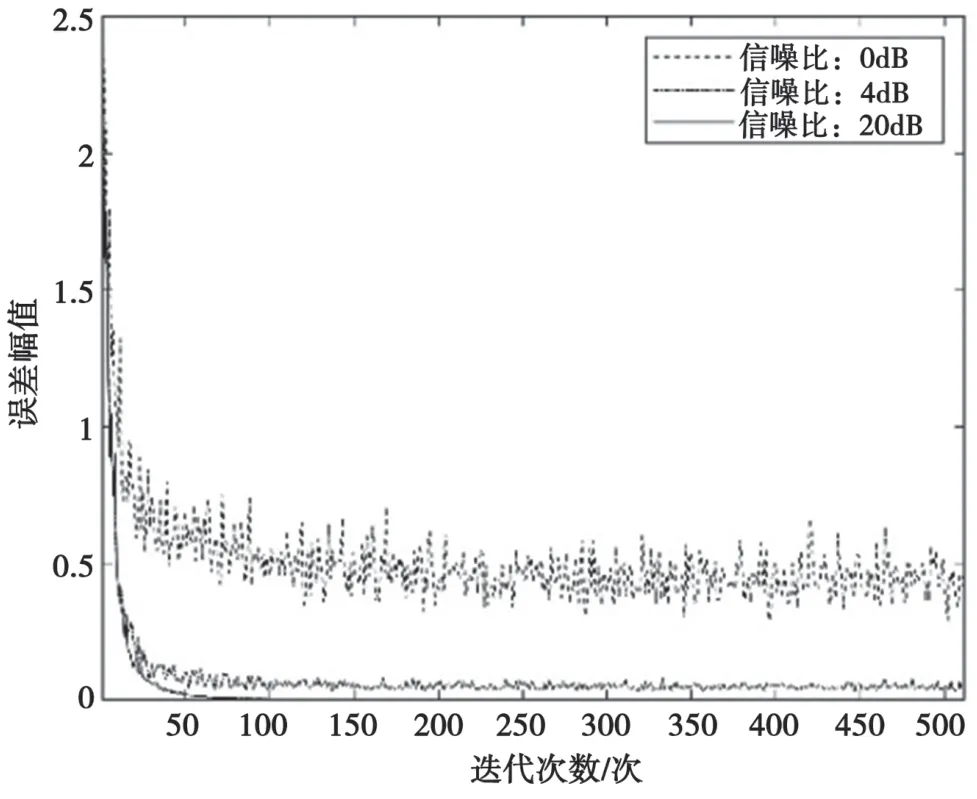
圖5 誤差收斂情況

3.4 波束方向分析

根據波束掃描得到的FABF和自適應算法得到的wDBF，可以得到混合波束賦形方案的波束圖，如圖6 所示。圖6 表明，自適應算法可以將主波束對準期望用戶方向，且在干擾方向形成了零陷，極大地抑制了干擾信號。

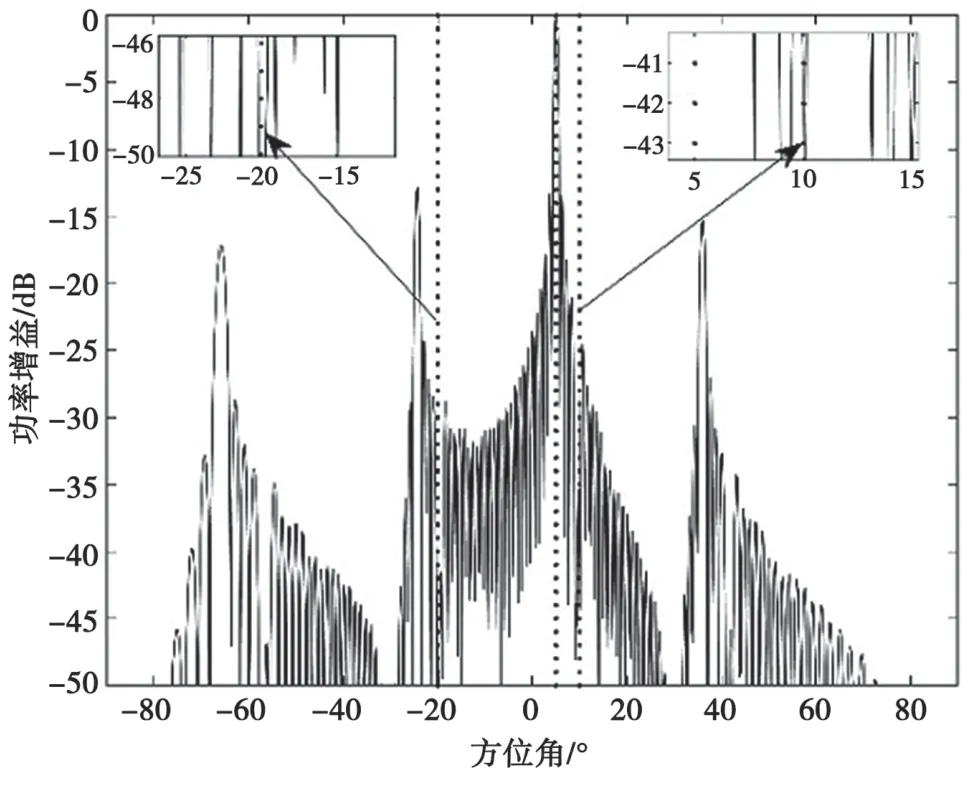
圖6 混合波束賦形波束

3.5 信干噪比和頻譜效率

信干噪比和頻譜效率分別如圖7 和圖8 所示。可以看出，信干噪比和頻譜效率隨著信噪比的增大而增大；所提出的混合波束賦形方案的信干噪比和頻譜效率性能遠遠高于純模擬波束賦形的性能，同時接近于純數字波束賦形的性能。

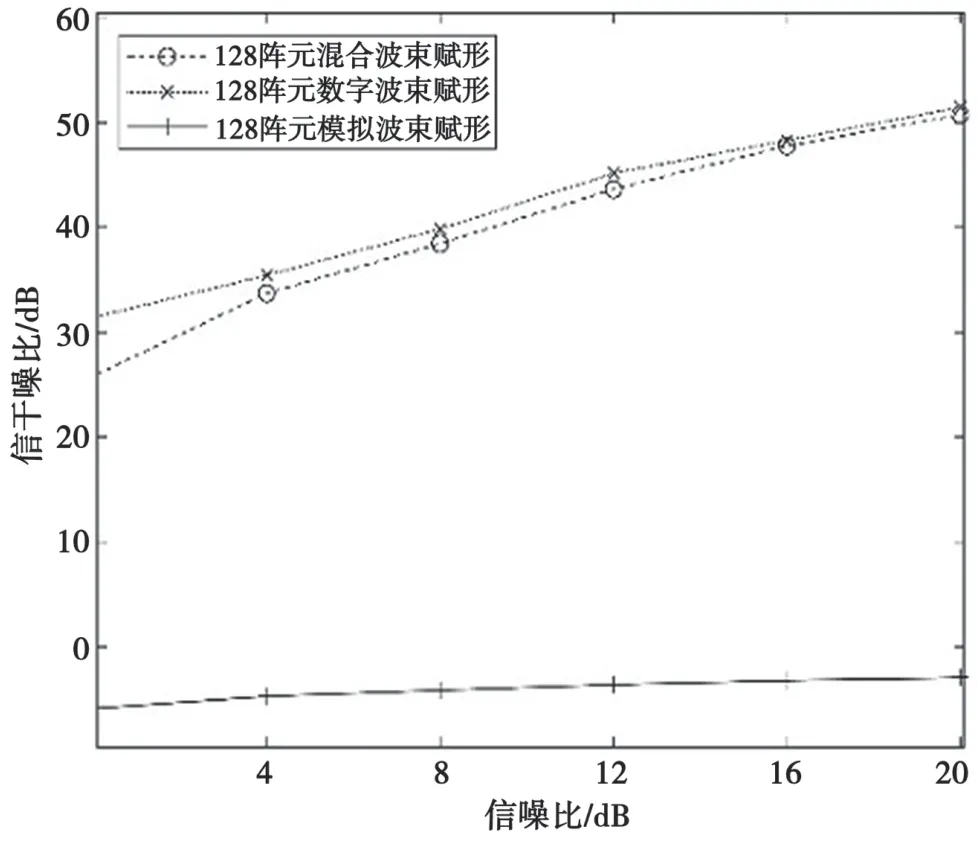
圖7 信干噪比仿真結果

圖8 頻譜效率仿真結果

4 結論

相較于傳統混合波束賦形技術需要進行高維信道估計和SVD 分解等高復雜度操作，本文將波束掃描和自適應算法結合，避免了信道估計和SVD 分解等高復雜度操作。第一階段的模擬域波束掃描得到與期望用戶方向最接近的波束；第二階段的自適應算法對第一階段得到的波束進行微調。仿真結果表明，當RF 鏈數僅為16 條時，混合波束賦形得到的波束圖能精確指向期望用戶，并在干擾用戶方向上產生較深的“零陷”；在信干噪比、頻譜效率等性能，所提出的混合波束賦形方案可以很好地逼近純數字波束賦形。