針對信息物理系統線性欺詐攻擊的水印加密策略

汪 迪， 李芳菲， 許思遙， 劉昌洪

（華東理工大學理學院，上海 200237）

隨著計算機和動力學系統方面研究的長足發展，信息物理系統（CPS）在當今社會中起著越來越不可或缺的作用[1-2]。CPS 作為一個集成計算、網絡和物理環境的復雜系統，可通過3C（計算機、通信、控制）技術的有機集成和深度協作，實現大型工程系統的實時感知、動態控制和信息服務[3]。由于信號通過無線通信通道時系統的安全性不能得到有效的保障，對CPS 的成功攻擊可能會造成巨大的損失，包括信息泄漏、工業流程暫停和基礎架構損壞等。因此，CPS 的安全性問題逐漸引起研究人員的關注[4]。

為了保證CPS 的安全運行，近十年來攻擊策略和防御機制受到了廣泛的關注。文獻[5]中，從攻擊者對系統開放資源破壞的角度出發，對CPS中的幾種攻擊模式進行了分類，其中拒絕服務（DoS）攻擊是最常見的攻擊類型之一，在這其中攻擊者試圖阻止通信通道，并使系統的估計誤差變大[6]。與DoS 攻擊相比，欺詐攻擊的重點是隱身性，隱身的攻擊在攻擊系統時不太可能被發現，從而使欺詐攻擊所造成的危害更加嚴重。文獻[7]研究了基于卡方檢測器的最優線性欺詐攻擊。文獻[8] 研究了基于KL 散度的隱身攻擊，該隱身攻擊獨立于任何特定的檢測方案，并分析了此類攻擊的隱身性和性能特征。文獻[9] 進一步證明了控制性能下降和攻擊隱身性之間的權衡。最近的研究提供了針對某些攻擊的防御策略。比如在文獻[10] 中，作者建議使用水印來達到檢測重放攻擊的目的，但同時犧牲了部分系統性能。

在信息物理系統的信息安全問題方面盡管已經取得了一些成果，但仍有一些問題需要進一步考慮。當提到基于KL 散度檢測器的CPS 的安全性問題時，由于KL 散度的復雜計算，一些代表性的結果僅考慮了系統為一維的情況[9-11]。另外，大多數研究僅考慮網絡攻擊問題，而沒有給出針對這種攻擊的防御或檢測策略。與卡方檢測器不同，KL 散度檢測器可以應用于非高斯分布的情況，因此具有廣泛的應用[12]，國內學者則進一步針對KL 散度檢測器提出了新型的線下欺詐攻擊[13]。然而，對基于KL 散度檢測器的CPS 的安全性問題的研究還遠遠不夠，尤其是在防御或檢測問題上。出于上述原因，本文考慮使用水印加密來針對帶有KL 散度檢測器的CPS 中的線性欺詐攻擊。

本文通過選擇適當的水印參數，證明了KL 散度檢測器在攻擊者不知道水印參數的統計特征時會觸發警報，結果表明本文方法對于給出的特定欺詐攻擊也有效，并且當攻擊者知道水印的統計特征時，水印的存在仍然可以削弱攻擊所造成攻擊效果，使得估計誤差方差盡可能控制在能容忍的范圍內。

1 問題設置

1.1 系統模型

1.2 KL 散度檢測器

1.3 攻擊模型

2 水印加密以及性能分析

2.1 水印加密模型

基于上述內容的討論，我們了解到KL 散度的大小取決于兩個正態分布的方差的差距，因此為了檢測上述線性欺詐攻擊，我們期望擴大攻擊存在時的新息序列的方差以幫助檢測器檢測攻擊的存在。我們給出水印加密的模塊，具體模式如圖1 所示，在系統發送新息序列之前，我們對數據進行預處理：

圖 1 系統運行階段的水印加密以及解密Fig. 1 Watermark encryption and decryption during system operation

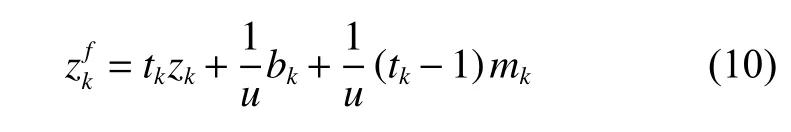
容易得到，它的均值為0，方差為：

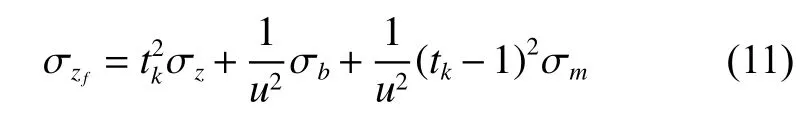
2.2 不同情況下的性能分析

故KL 散度檢測器會觸發警報，從而發現攻擊的存在，證畢。

進一步可以看到由于KL 散度在一側單調遞增，若水印參數較大，則可以使KL 散度值進一步變大，使得攻擊的暴露速度加快，但同時較大的參數會使得容易被攻擊者發現水印的存在。同時基于上述定理，可以得知水印的存在可以有效地使文獻[13] 中的最優攻擊被檢測器發現。

2.2.2 完全了解水印信息 因較大的水印參數可能使得水印被攻擊者發現，若攻擊者知道了水印參數u 以及mk的方差σm，此時攻擊者會重新構造攻擊，從而避開KL 散度檢測器[15]。即使攻擊者重構攻擊，水印的存在會使得攻擊的效果變差，即估計誤差方差仍被控制在一定范圍內。在此之前需要得到估計誤差方差關于攻擊參數tk的表達式：

引理 1：當有水印存在時，在如式（5）的攻擊形式下，估計誤差方差的表達式為：

通過引理1 以及定理2 可知，水印的存在可以降低估計誤差方差，從而減小對系統的影響，在實際運用中，適當大小的水印參數即可限制攻擊者的策略，并非要求趨向于無窮。

3 數值模擬

我們比較了不同水印情況下對于線性欺騙攻擊的影響，考慮下面這樣的系統，系統參數為a=0.7，c=0.3，p=0.5 和 q=0.1，KL 散度檢測器的閾值 δ=1。

圖2 示出了不同的水印參數對于KL 散度檢測器的影響，其中黑線為攻擊不存在時的KL 散度值，藍線，紅線和綠線分別表示原最優攻擊存在時參數分別為 u=0.5，σm=1；u=0.5，σm=4；u=0.5，σm=8 時，KL散度檢測器所得到的KL 散的值的變化曲線。結果表明，在存在最佳攻擊的情況下，水印的存在可以增加KL 散度的值，從而觸發警報。

當攻擊者完全了解水印的存在，即知道水印的協方差矩陣并重構最佳攻擊策略時，我們分析水印參數對攻擊者造成的估計誤差協方差的影響。對于相同的KL 散度閾值，圖3 給出了在重構的最優線性欺詐攻擊下，不同水印參數的影響下，遠程估計誤差協方差的演變。其中紅線表示任意水印存在、攻擊不存在時的估計誤差方差，黃線，黑線，藍線和綠線分別表示當存在攻擊而不加水印時的遠程估計誤差協方差。從圖3 可以看出，水印參數越大，估計的誤差協方差越小。根據定理2 的結論，參數的值變大，重構攻擊可能引起的估計誤差協方差變小。根據仿真結果，當u=0.5，σm=1 000 時，估計誤差方差的值趨向于攻擊不存在時的估計誤差方差的值。

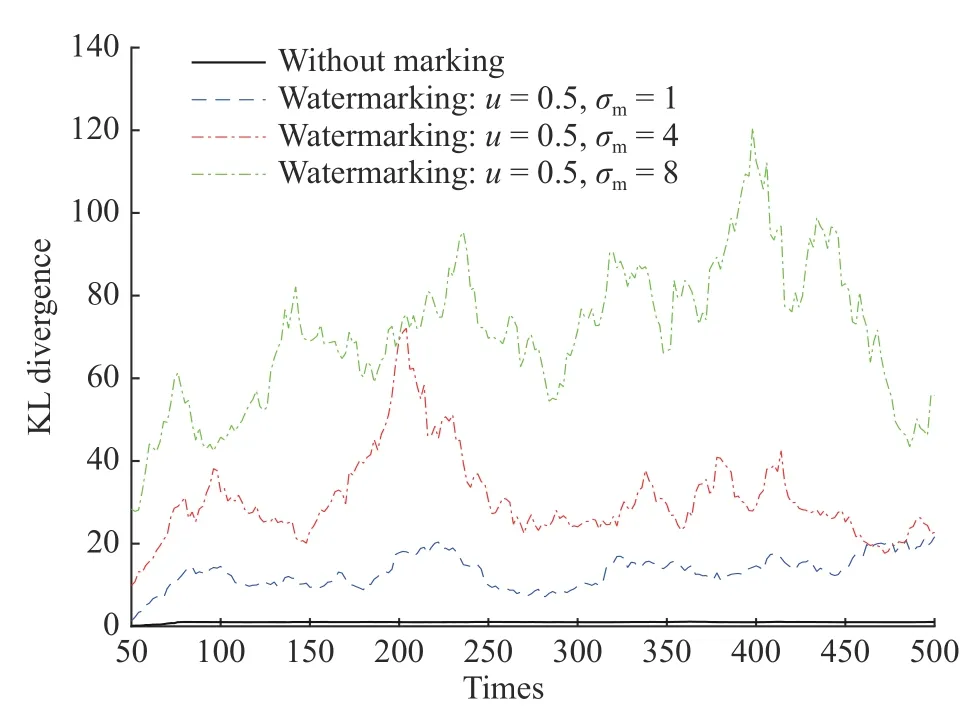
圖 2 不同程度的水印參數對KL 散度值的影響Fig. 2 Influence of different degrees of watermark parameters on KL divergence value

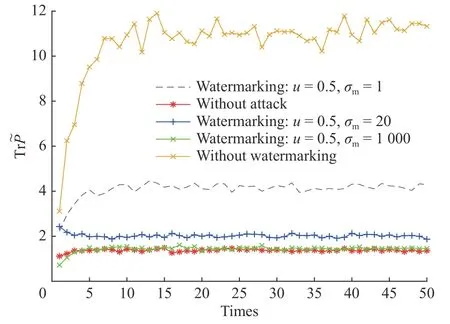
圖 3 不同水印參數下，重構的最優欺詐攻擊所能造成的估計誤差方差的大小比較Fig. 3 Comparison of estimated error variances caused by reconstructed optimal deception attacks under different watermark parameters

4 結 論

本文使用水印加密和解密來幫助KL 散度檢測器在遠程狀態估計方案中識別線性欺騙攻擊。與以前的結果不同，當不存在攻擊時，我們使用加水印加密和解密的過程來恢復傳輸的數據，以避免影響系統的估計性能。針對不同的線性攻擊場景，進一步分析了該方法的可靠性及其對估計誤差的影響。當攻擊者采取最佳線性欺騙攻擊時，可以證明該攻擊將觸發警報，事實上在適當的參數選擇下，KL 散度的值趨于正無窮大。當攻擊者重構針對水印的最佳線性欺詐攻擊時，通過選擇適當的參數，這種攻擊只能對系統性能產生有限的影響。總結上述情況并獲得最佳參數選擇，可以削弱攻擊者的影響或使KL 散度檢測器盡快檢測到攻擊。同時本文提供了一個仿真示例，以驗證本文的方法對線性欺騙攻擊的影響。