基于行為預測的水下無人機一致性時延處理

牟春曉，李廣儒，蘭蔚

（大連海事大學航海學院，遼寧 大連 116026）

水下無人機編隊相較其他海洋觀測手段，具有靈活性高、觀測效果可靠、成本低的優點。其工作環境相比空中無人機有很大的差異。首先，水下無人機的工作阻力和所受干擾要遠大于空中無人機；其次，水下無人機編隊的通信會極大地受到海水的影響，從而發生信息傳輸的延遲、失真或丟失。因此，研究水下無人機編隊的通信時延問題，對發展新時代的海洋戰略有著重要的意義。

Kumar 等學者提出了一種針對一般六自由度非對稱自主水下航行器的離散時滯控制（DTDC）定律。劉成林等根據不同的分析方法，介紹了關于具有通信時延的多個體系統一致性問題的結果，并對各種分析方法的特點進行了比較；孟憲松等針對多水下機器人編隊控制中的水下無線通信問題，提出了一種基于調度的水下無線環狀媒介訪問控制協議；季蕾、樊春霞為研究發生信息傳輸時延情況下多無人機的編隊控制器設計問題，使用服從Bernoulli 分布的隨機變量描述時延，推導出與無人機編隊控制時延相關的穩定性條件；李實吉等針對時延問題，提出了基于卷地毯式搜索的組網規劃算法；劉明等針對同時具有網絡誘導時延和數據包丟失的網絡控制系統，提出了使得該系統達到指數穩定的動態輸出反饋控制器的設計方法；何呂龍等針對無人機集群在有向通信拓撲和存在通信時延條件下的時變編隊控制問題，設計了分布式編隊控制協議。

本文在上述研究的基礎上，使用二階系統來描述水下無人機的動力學模型，通過對比有無時延條件下的無人機編隊控制結果，分析時延在實際應用中的重要影響。給出了一種基于行為預測的一致性時延處理方法，應用此方法對水下無人機編隊進行了仿真模擬，結果顯示，此方法可以顯著減小時延對編隊帶來的影響。

1 系統模型

1.1 單體無人機動力學模型

規定：無人機在編隊控制中視為質點；綜合觀測需求與安全的考慮，無人機需要與觀測點保持安全觀測距離；仿真環境為靜水。

單體無人機在靜水中的動力學模型如下：

其中，X1、X2∈R3為狀態變量，k為阻力系數，m為質量，u∈R3為系統輸入，Q為附加常量。

得到

假設人工勢場函數的輸入為δ，則輸出ζ可以表示為：

其中，ζ,δ∈R3，η是吸引系數，μ是排斥系數。

1.2 無人機組動力學模型

設置編隊成員間人工勢場如下：

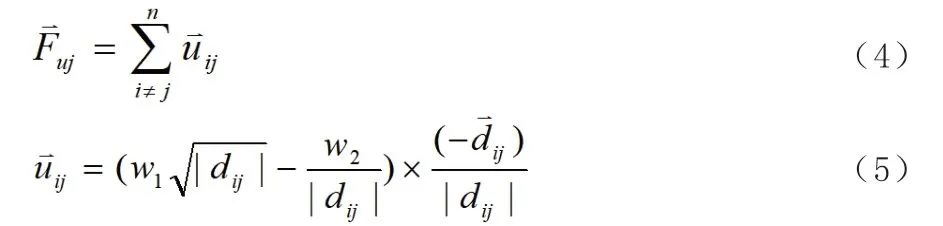
其中，n為無人機組的無人機個數，為無人機i與j之間的作用力，dij為無人機i與j之間的距離向量，w1,w2為待定系數。無人機組成員間的期望距離DI為：

個體數為n的無人機編隊的動力學模型為：

2 時延問題

水下通信受傳輸介質的影響，信息傳輸時間延遲發生的概率要遠遠大于普通的以空氣為傳輸介質的通信。一般來說，淺海（小于200 米）通信延遲有幾百毫秒，深海（大于200 米）通信則可以達到幾十微秒甚至幾秒的量級。在這種量級的干擾下，編隊的通信出錯會直接影響編隊的協同控制，輕則影響任務的完成質量，重則造成設備財產的損失。

首先，無人機對于自身數據的感知是實時的。對于上述控制系統，設置離散系統采樣時間為ε，表示無人機i與無人機j之間的通信傳輸時延，且同一時刻無人機i接收無人機j信息的時延與無人機j接收無人機i信息的時延相同，即

對于離散時間系統，時間延遲應至少為一個采樣周期。考慮到深海時延的期望數量級，不妨規定：χ∈(ε,2ε)在任意采樣點t0時刻，無人機j向無人機i發送其采樣時刻和自身數據，則無人機i會在時刻收到無人機j在t0時刻的數據。無人機i會立刻根據此數據進行自身姿態的調整，并在下一個采樣點(t0+2ε)時刻發送自身姿態數據。其示意圖如圖1 所示。

圖1 無人機間通信傳輸示意圖

帶時延的無人機組動力學模型為：

式（9）是一個強耦合的多個體非線性時滯系統。

3 行為預測方法

通過在發送端中添加信息發送時刻，與接收端本機時間對比來推知此條信息傳輸的時延。時延是否固定，在上述的討論區間內對系統控制并無影響。本文為簡明起見，以下所述時延皆為固定時延。

在t0+χij時刻，無人機i接收到無人機j的發送時刻和姿態信息。理論上來說，只要根據接收到的信息預測出t0+χij時刻無人機j的位置，就可以消除時延帶來的影響。預測越精確，時延的影響就越小。

t0至t0+(χij?ε)時刻，無人機j對自身的姿態調整是根據目標點和其他無人機在t0?2ε時刻的位置信息所進行的，此信息則在t0?(χij?ε)時刻能被無人機i感知。則無人機j在t0+(χij?ε)時刻的位置信息可推。

t0+(χij?ε)至t0+χij時刻，無人機j對自身的姿態調整是根據目標點和其他無人機在t0?ε時刻的位置信息所進行的，此信息則在t0+(χij?ε)時刻能被無人機i感知。則無人機j在t0+χij時刻的位置信息可推。

綜上所述，根據t0+χij時刻無人機j的報文，預測時刻無人機j的位置信息為：

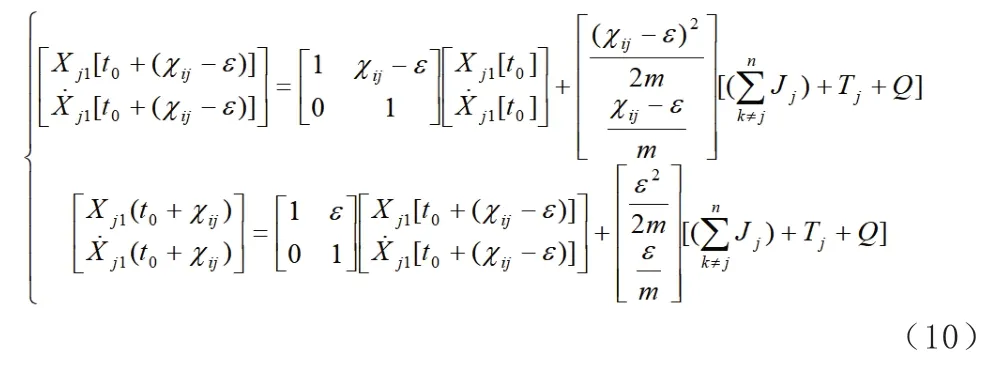
4 仿真分析（表1）

表1 參數賦值

目標點為(500,200,200)，時延系統輸出出現振蕩，不再完全穩定，以平衡點為中心的鄰域范圍內做往復運動。無人機間距離出現較大波動，嚴重影響了觀測網絡的整體穩定性。根據式（10），設計時延處理器。輸出結果如圖2 所示。

圖2 雙無人機系統輸出結果對比

定義無人機組目標合圍的振蕩系數?，

有無時延預測的系統的振蕩系數變化如圖3 所示。

可見，有時延預測的系統有著更低的振蕩系數，反映了系統更好的收斂性。無時延預測系統的二階導數在約600s出現突增，有時延系統的二階導數則幾乎沒有發生變化。經計算，有時延預測的穩態振蕩系數的一階導數比無時延預測平均下降了24.93%。

5 結語

本文分析了水下無人機系統在目標合圍任務中的控制過程，圍繞時間延遲建立了水下無人機系統的二階離散時間模型。通過對比有無時延條件下控制系統的輸出變化，說明了時間延遲會對無人機系統的穩定性造成極大的影響，如果考慮實際情況中的障礙物與海流，那么，時間延遲將是水下觀測網絡需要面臨的巨大挑戰。設計了時延處理器，將新的輸出結果與不加時延處理器的結果進行比較，驗證了基于行為預測的時延處理方法更佳。

圖3 時延預測效果對比