基于智能算法的橋梁結構邊界特性識別

梅 沖,周 杰,杜震超

(武漢輕工工程技術有限公司,武漢 430073)

橋梁結構的精確有限元模擬可以為橋梁設計、監測、加固決策提供可靠依據，在采用有限元程序對橋梁結構進行模擬時，橋梁支座的剛度直接影響結構在靜載下的位移響應[1,2]。然而，由于支座安放角度、施工質量、產品規格變異以及長時間服役后橡膠的老化、盆式支座的磨損等原因，直接采用支座生產廠家提供的數據建立有限元模型的約束，會存在一定的誤差，特別是在潮濕、嚴寒、高溫等易加快橡膠老化的環境下，支座對梁體的約束情況與出廠時可能存在較大誤差[3]。

如何準確模擬結構的實際邊界條件，為結構的設計、運維提供可靠依據已經成為近年來工程界的迫切需求，也逐漸轉化為學術界的研究熱點[4]。

其中一種可行的方案是，根據結構在實際荷載下的位移響應，反演結構的邊界約束情況[5-7]。在靜載作用下，結構發生的位移由兩部分組成：支座的彈性形變和結構本身的受力形變，而結構的形變與支座情況相同，在長時間服役后會出現結構變異，從而影響結構的位移響應。因此結構在靜載下發生位移時，如何判別位移成為研究難點。

為解決上述問題，采用智能優化算法，根據結構在靜載下的位移響應，反演結構的變異和支座的邊界特性。并且以一個箱梁單梁為案例，分析了該文推薦的算法及識別流程，然后采用所述方法對其進行了優化，對比了優化前后的支座剛度以及結構的位移響應差值。

1 橋梁結構邊界特性識別原理

1.1 結構反演原理

根據結構的實際參數，如尺寸、物理性能(彈性模量密度)等，計算結構在荷載下的靜動力響應，屬于結構計算的正問題。而根據結構在已知荷載下的響應，反算結構的物理參數、尺寸等信息，屬于結構反演。在確定性模型中，結構能夠進行反演的基本假設是在確定荷載下，每組結構參數都存在一個且唯一的響應。

通過一定算法不斷調整結構的設計參數，使之響應與測得響應相一致的過程稱為結構參數識別。

準確識別結構邊界條件，對結構的后期運維至關重要。為得到精確的結構支撐剛度，提出了利用遺傳算法，采用反演方法分析結構邊界條件的流程，并在實際案例上進行了驗證。結果表明，智能算法配合反演的方法可以準確識別結構邊界剛度，為結構的運營維護提供了參考。

1.2 結構參數反演流程

結構參數識別的一般步驟是：

1)根據設計圖紙確定初始結構參數，并根據該組參數建立有限元模型；

2)對實際結構進行靜動力響應測試；

3)根據測試結果采用優化算法調整設計參數，計算在新參數下的結構響應；

4)根據優化參數下結構響應與結構實際響應的差值，根據算法設定的準則確定下一組優化參數；

5)運行步驟4直至滿足算法終止條件。

該文選擇的終止條件為算法迭代次數達到上限。

2 遺傳算法

遺傳算法是一種群智能算法，受啟發于自然界中生物進化過程。在微觀層面，生物基因經過復制、交叉、變異等過程，從而在宏觀層面表現出個體逐漸適應環境和優勝劣汰的行為。

遺傳算法[8-10]模擬生物界進化過程，問題的一個可行(不一定是最優)解對應一個個體，問題自變量的維度對應個體基因中染色體的條數。每條染色體上有很多基因點位，整個基因確定了個體所處位置，而個體在評價函數中的位置確定了其適應性大小。

遺傳算法的步驟：

1)根據實際問題初始化一群個體，個體數量，個體的維度等信息；

2)計算每個個體的適應度，根據適應度對個體進行排序；

3)復制一定比例的個體作為父代；

4)父代與所有個體隨機匹配然后交換一組或多組染色體，形成子代；

5)對部分子代或父代的隨機個別基因點位進行變異；

6)計算所有父代子代的適應度，并采用輪盤賭等法則選擇合適的子代；

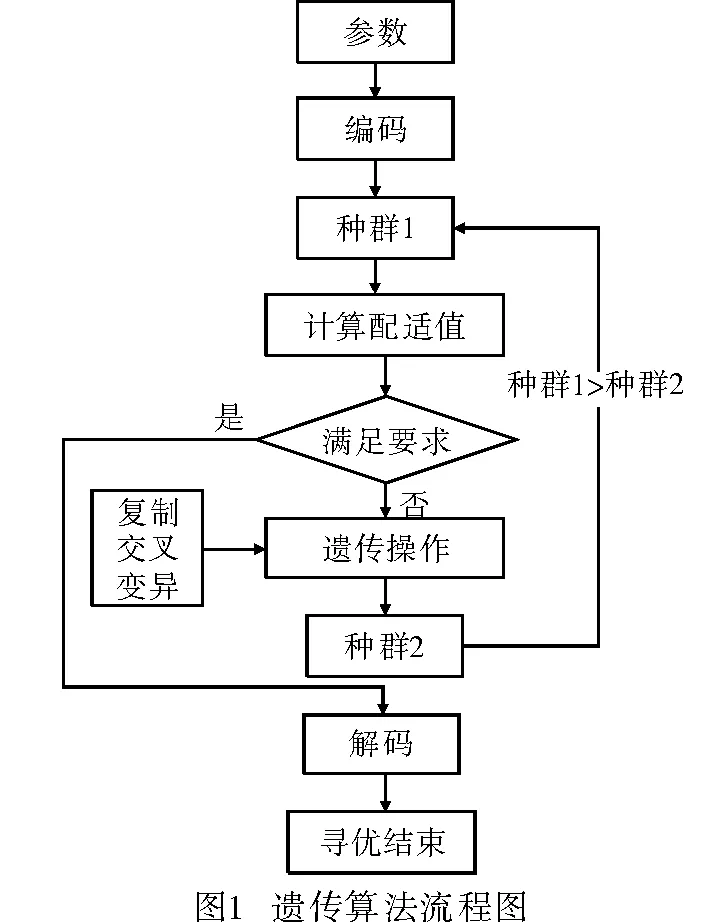
7)判斷子代的適應度是否滿足迭代終止條件，是則退出循環，輸出結果，否則進入步驟2進行下一步迭代計算，直至滿足迭代終止條件，見圖1。

3 案例分析

為驗證所提算法的可行性，以一個簡直梁為背景，以邊界特性參數和梁體剛度為識別變量，采用遺傳算法對結構參數進行識別，結構的概況為：結構為30 m跨徑單梁，截面形式為箱型，箱梁毛截面幾何特性見表1，尺寸見圖2。

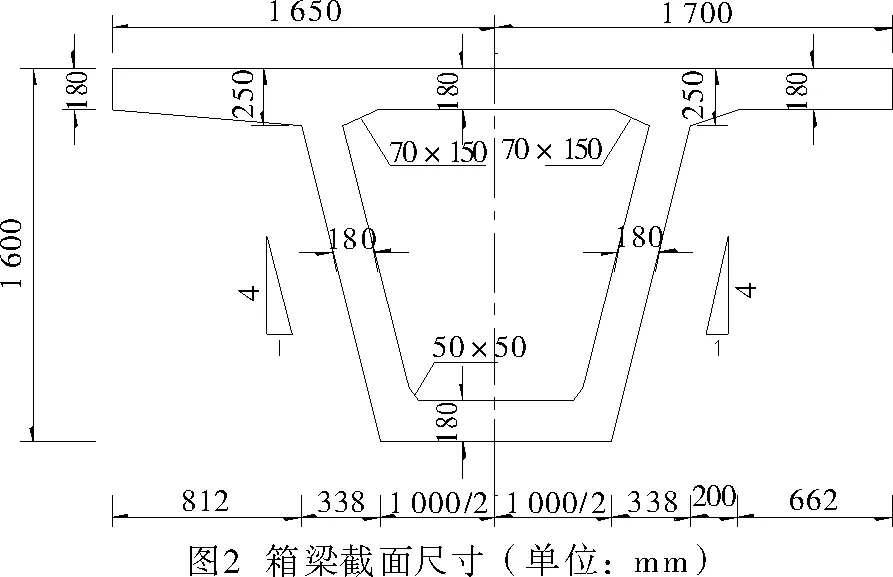
表1 箱梁毛截面幾何特性

結構材料：

1)混凝土：預制梁及現澆濕接縫、橫梁為C50、現澆調平層為C40。

2)預應力鋼絞線：采用鋼絞線φs15.2，fpk=1 860 MPa，Ep=1.95×105MPa。

3)普通鋼筋：采用HRB335，fsk=335 MPa，ES=2.0×105MPa。

實驗：

為驗證結構在荷載下的受力性能，對其進行了靜載實驗。依據相關規范，本次試驗對梁體的L/2跨(A-A截面)和L/4跨(B-B)各布置9個應變測點和3個撓度測點，各截面測點布置如圖3所示。

由于條件限制，無法在支座處安裝位移計，因此，無法直接判斷結構支座的位移。

對主梁施加荷載，梁體產生的位移如表2所示。

表2 結構實測位移值

梁中部測得的撓度由兩部分組成：梁在荷載下的變形和支座的位移。由于結構混凝土的碳化等原因，根據設計圖紙直接采用有限元計算的位移與實際位移存在差異。因此需要將結構材料彈性模量和支座剛度同時作為變量進行優化。

參數識別：

根據設計圖紙，并采用參數化建模方法建立初始有限元模型，采用梁單元對結構進行模擬。通過不斷調用有限元程序改變模型彈性支撐剛度和材料彈性模量來逼近結構真實位移。

在優化算法中，需要設定一個參數來衡量有限元模擬響應與真實響應之間的吻合程度。采用的位移差值向量的2-范數，如下式所示

E=|Dfe-De|2

式中,E為目標函數值;Dfe為結構有限元模型計算的位移向量;De為結構在實際荷載下測得的位移向量。

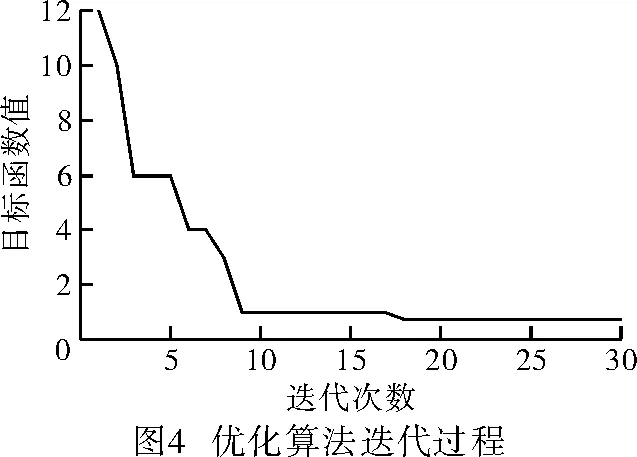
采用遺傳算法對目標函數進行尋優，尋優過程如圖4所示。

從圖中可以看出，算法優化速度較快，在18次后不再進化，認為尋找到了目標函數的最優解。

最優解為支座剛度K=882 000 kN/m，混凝土相對彈性模型為0.97(在優化程序中，為便于計算，將優化彈性模量與初始彈性模量的比值作為優化變量)。優化結果如表3所示。

從表3中可以看出，優化后3點的位移值均有較大幅度的減小，且最終的誤差小于1%。表明優化結果的彈性模量和剛度具有較高精度。彈性模型經過優化后，有小幅度減小，可能原因是經過長時間環境作用，混凝土出現了一定程度的碳化。

表3 優化結果對比

4 結 論

結構邊界特性的精確模擬至關重要，通過反演與群智能算法相結合的方式，對一個箱梁支座剛度以及結構的彈性模型進行了聯合反演。在未優化前，結構初始有限元模型的計算結果和實測結果之間的差值達到了11%以上，通過遺傳算法的優化，三處的結構位移誤差均降到了1%以下，提高了有限元的擬合精度，研究可為有限元的精確模擬提供參考。