考慮應力松弛效應的球頭-錐面密封性能分析

王莉娜, 孫恒超, 孫 偉, 綦 磊, 孫立臣, 孟冬輝

(1.北京衛星環境工程研究所, 北京 100094；2.中國空間技術研究院 通信衛星事業部, 北京100094)

球頭-錐面密封結構易于拆裝，且具有良好的密封性能，廣泛應用于衛星推進系統的管路連接中，因此，近年來有關其性能的研究開始得到學者們的關注[1-3]. 周等[3]采用有限元方法計算不同預緊力條件下球面密封結構中密封面間的接觸壓力及密封寬度，并在此基礎上，結合Roth模型建立了分子流狀態下球面密封泄漏率計算模型，獲得球面密封的泄漏率. 韓等[4]采用有限元方法獲得不同流體壓力作用下球頭-錐面間的接觸應力及密封寬度，并將上述結果代入基于Roth泄漏模型推導出的考慮應力松弛的泄漏率計算公式中，以計算球頭-錐面密封的泄漏率.

應力松弛效應會對材料的性能產生較大影響，進而會對有密封或緊固要求，且長期存放的零部件產生顯著影響[5-9]. 王等[10]采用有限元方法建立了常溫下螺栓應力松弛模型，并采用這一模型分析了不同因素影響下螺栓應力隨蠕變時間增長的變化規律. Liu等[11]采用試驗方法研究了室溫環境下鋼的蠕變性能，研究結果表明較大的應力、較長的蠕變時間、較低的硬度以及不均勻的微觀結構等因素均會增大蠕變應變. Jiang等[12]建立了蒸汽輪機中螺母連接部件的有限元模型，并采用這一模型研究了蠕變效應對螺母連接部件密封性能的影響規律. Mann等[13]建立了螺栓凸緣連接結構的有限元模型，并采用這一模型分析了高溫環境下蠕變松弛效應對其性能的影響規律. Silva等[14]采用試驗方法研究了提升溫度對多種制備方法獲得的PTFE墊片蠕變松弛性能的影響. Gordon等[15]采用試驗方法分析了新型墊片蠕變松弛的本構模型，并獲得填充材料及扭轉力等參數對墊片性能的影響規律. Maximov等[16]采用有限元方法分析了室溫環境下鋁合金材料的蠕變特性，并在此基礎上提出了描述殘余松弛應力的數學模型，這一模型可以快速確定不同蠕變時間下鋁合金材料的殘余應力. Mao等[17]采用有限元方法研究了蠕變條件下，凸緣厚度及螺栓預緊力對凸緣密封性能的影響，研究結果表明蠕變效應會對凸緣密封的性能產生顯著影響.

以往研究雖然考慮應力松弛效應的影響，但多是在泄漏率計算公式中計入應力松弛效應的影響，而螺母殘余預緊應力及球頭-錐面間接觸應力等參數保持不變的條件下獲得的，這必然會對計算結果的精度產生較大的影響.

基于此，本文在球頭-錐面有限元模型中計入應力松弛效應的影響，獲得螺母殘余預緊應力及球頭-錐面間接觸應力隨蠕變時間增長的變化規律，然后基于Roth泄漏模型推導的泄漏率公式計算獲得球頭-錐面密封泄漏率隨蠕變時間增長的變化規律.

1 理論模型

球頭-錐面密封性能分析主要包含兩部分內容：一是建立考慮應力松弛效應的球頭-錐面密封性能分析有限元模型；二是基于Roth提出的泄漏模型，推導出適用于球頭-錐面密封泄漏性能計算的理論公式.

1.1 球頭-錐面密封力學分析模型

球頭-錐面密封結構示意圖如圖1所示，其主要由管路、球頭、錐面及螺母4部分組成. 螺母與錐面之間為螺紋連接，在螺母上施加擰緊力矩時，螺母將球頭沿軸向壓向錐面，球面與錐面表面初始狀態的線接觸也會隨著球頭與錐面間的壓縮貼合轉變為面接觸. 兩個面的相互擠壓使接觸面上的微觀間歇被填滿，實現密封.

管路、球頭、錐面三個零件均為軸對稱結構，螺母一般為正六角結構，本文分析中忽略了螺母邊角，并認為螺母對球頭的預緊力繞z軸均布. 由于球頭-錐面密封結構具有周向循環的結構特征，為減少計算工作量以提高工作效率，可以建立如圖2所示的網格模型，模型繞z軸的夾角，即循環特征結構在圓周方向上的尺度為3°，其邊界條件具體如下：

球頭、錐面及螺母截面1處施加循環對稱約束；螺母外表面2處及錐面右側端面3處均施加x、y和z三個方向的位移約束；球頭及錐面內表面4處均施加流體壓力載荷；管路外表面5處施加y和z方向的位移約束；根據螺紋特點，將與初始預緊力矩對應的預緊力施加在螺母處的截面6上，預緊力方向沿z軸并指向錐面；球頭-錐面密封結構整體施加均勻溫度載荷. 另外，分別在螺母與球頭、螺母與錐面、球頭與錐面之間建立接觸對，并設置相應的摩擦系數.

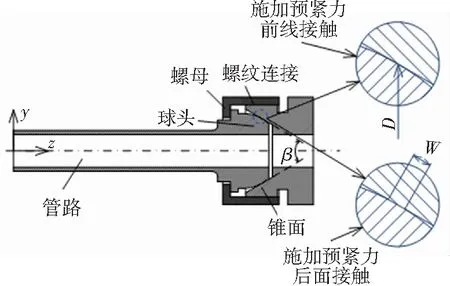
圖1 球頭-錐面密封結構示意圖

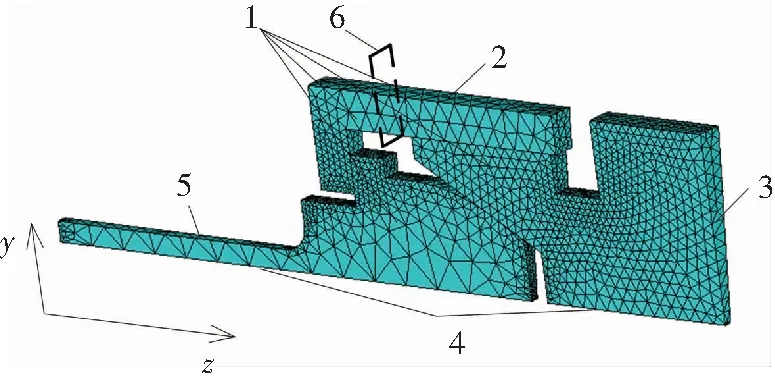
圖2 球頭-錐面密封性能分析有限元模型

Fig.2 Finite element model for performance analysis of globe-cone sealing

采用第一階段應變強化蠕變模型及其理論公式來模擬預緊螺母的應力松弛特性，理論公式為

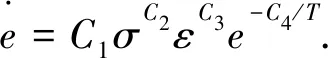
(1)

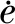
通過上述有限元模型可以求解考慮應力松弛狀態下的球頭-錐面密封接觸平均應力、密封面寬度等參數，并作為泄漏分析的輸入.

1.2 泄漏模型

依據Roth提出的泄漏模型(如圖3所示)，可以將球頭-錐面間形成的泄漏通道視為由若干橫截面積恒定且為等腰三角形并聯而成，球頭-錐面間總泄漏為所有泄漏通道的疊加.

在施加初始預緊力前，球頭與錐面僅在截面c處接觸，D為密封環直徑. 隨著施加預緊力，球頭與錐面在z方向上接觸區域擴展，在截面a和截面b為接觸區域起點，截面a和截面b之間球頭與錐面均接觸，該泄漏通道的長度即為密封面的寬度W. 因球頭-錐面密封結構的總漏率小于1×10-6Pa·m3/s，因此泄漏通道間的氣體流動可以視為分子流.

單個橫截面為等腰三角形的微型柱體流導可以表示為[1]

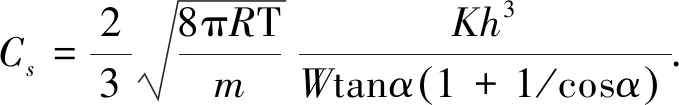
(2)

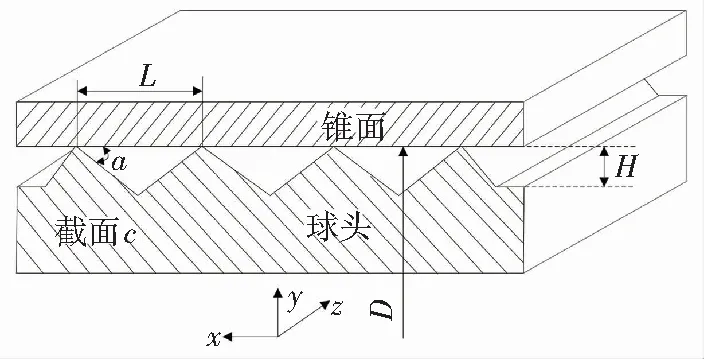
(a)施加初始預緊力前

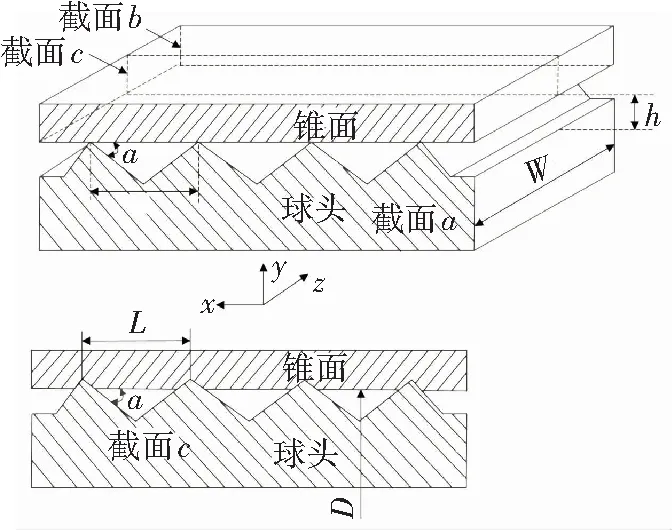
(b)施加初始預緊力后

式中：α為等腰三角形底角；h為實際工作狀態下微型漏孔底邊上的高；W為密封面的寬度；m為氣體分子質量；R為氣體常數；T為氣體的絕對溫度；K為形狀修正系數.

對于直徑為D的密封環，其密封面上漏孔的個數為

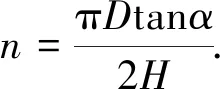
(3)

式中：H為初始狀態下微型漏孔底邊上的高.

綜合式(3)和式(2)，可以獲得整個密封面的總流導為

根據文獻[1]

式中：σm為密封面上的平均應力；Ks為反映密封面上較軟材料密封性能的系數. 則總漏率可以表示為

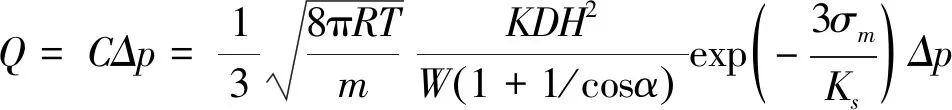
Roth指出接觸形成的泄漏路徑橫截面的典型形式是底角α=4°的等腰三角形，此時形狀修正系數K=1.7. 那么，考慮應力松弛效應條件下的總漏率可以表示為

式中：σm為考慮應力松弛效應條件下球頭-錐面間的平均應力；D為密封環直徑；W為密封面的寬度. 其中，σm、D及W均需通過有限元仿真分析獲得. 上式反映出球頭-錐面接頭處總漏率受到球頭-錐面間接觸應力、密封面寬度等的影響，工程實際中球頭-錐面密封結構的接觸應力、密封面寬度是隨著時間變化的，先前工作并未綜合考慮這一變化，所以對漏率的計算結果精度存在偏差.

綜上，本文中考慮應力松弛效應球頭-錐面密封漏率計算流程如圖4所示.

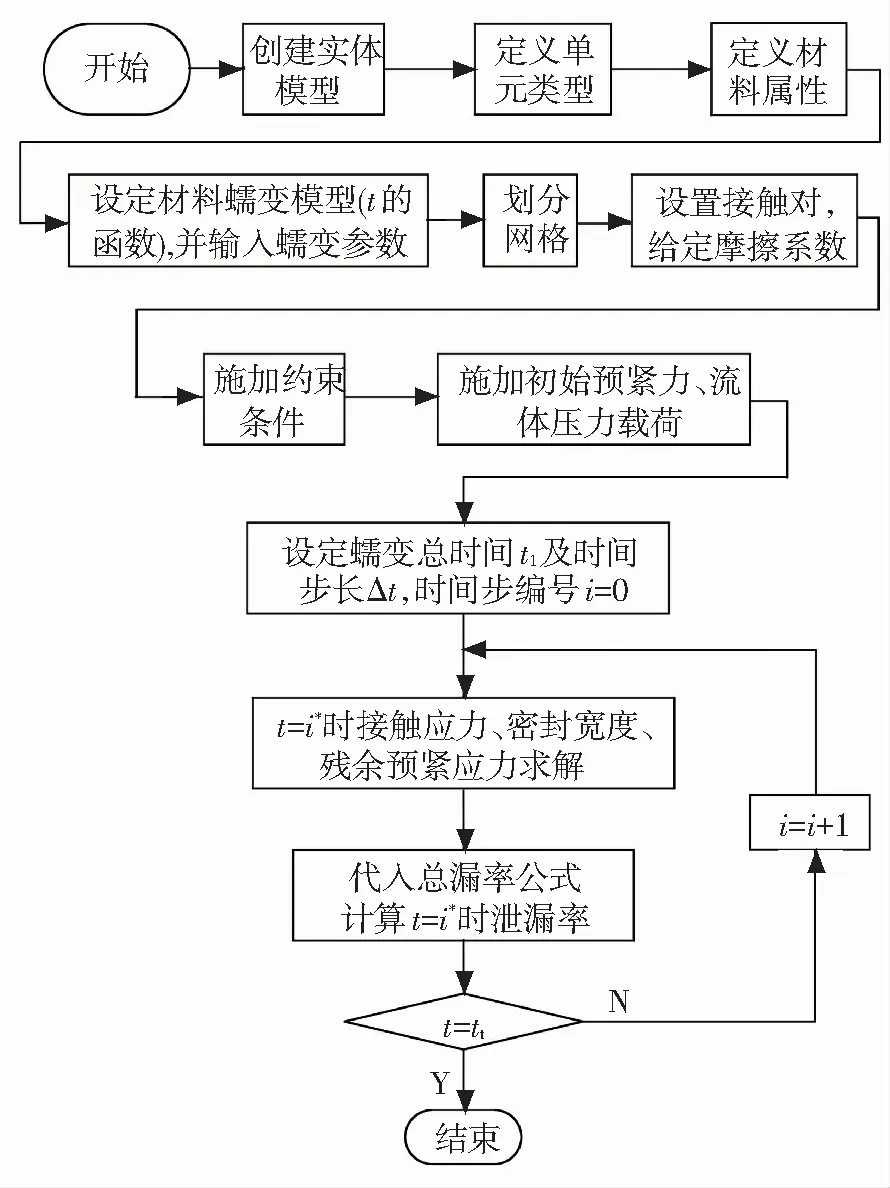
圖4 考慮應力松弛效應球頭-錐面密封漏率計算流程

Fig.4 Calculation of globe-cone seal leakage rate considering stress relaxation

本文球頭-錐面密封結構處于常溫氦檢漏狀態，因此，相關參數分別取為：T=293 K；m=4；R=8314.4；H=0.8 μm；Ks=103 MPa.

2 計算結果與討論

2.1 考慮應力松弛效應與否的球頭-錐面密封結構性能對比

這部分內容在錐面傾斜角度β=60°、摩擦系數為0.15、螺母預緊力為10.5 kN及流體絕對壓力為2 MPa條件下(下同)，對比考慮應力松弛效應與否的球頭-錐面密封性能的差異.

圖5所示為考慮應力松弛效應與否的球頭-錐面密封性能的對比，從圖中可以看出，除蠕變時刻為0的情況，不考慮應力松弛效應的球頭-錐面密封的殘余預緊應力及球頭-錐面間的接觸應力均大于考慮應力松弛效應的球頭-錐面密封的相關性能. 這是因為產生了應力松弛現象，即在維持恒定變形的材料中，應力會隨蠕變時間的增長而減小. 從圖中還可以看出，考慮應力松弛效應影響下，球頭-錐面密封中螺母殘余預緊應力及球頭-錐面間的接觸應力均會隨蠕變時間的增長而減小，產生這種現象的原因同上所述. 另外，從圖中還可以看出蠕變時間愈長，考慮應力松弛效應與否條件下獲得的螺母殘余預緊應力及球頭-錐面間的接觸應力間的差異愈大，這是容易理解的.

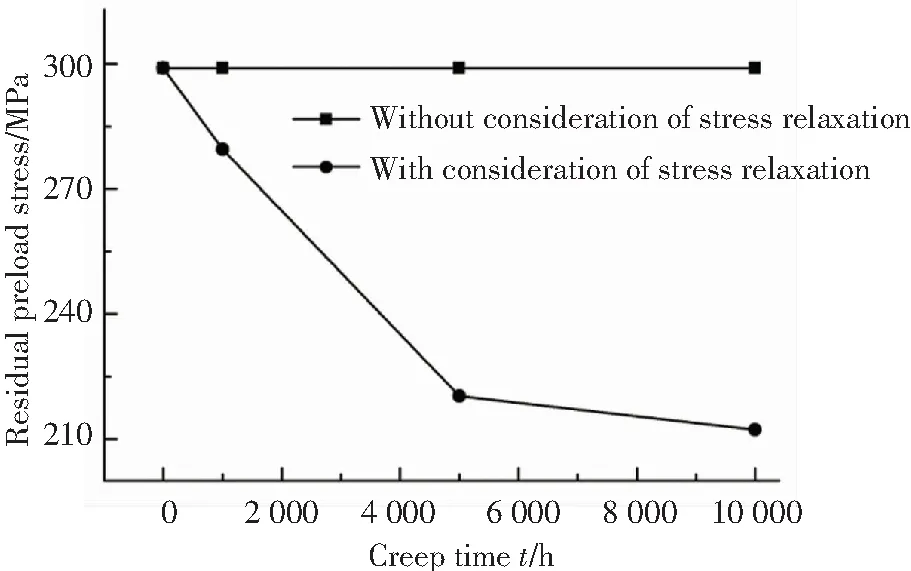
(a)螺母殘余預緊應力

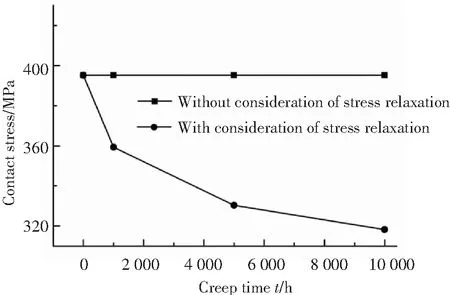
(b)球頭-錐面間接觸應力

Fig.5 Comparison of globe-cone seal performance with and without consideration of stress relaxation

2.2 考慮應力松弛效應的球頭-錐面密封性能分析

2.2.1 預緊力的影響

球頭-錐面密封螺母殘余預緊應力隨蠕變時間的變化規律如圖6所示，從圖中可以看出隨螺母預緊力的增大，球頭-錐面密封螺母殘余預緊應力會隨之增大，這表明螺母預緊力與其殘余預緊應力正相關. 從圖中還可以看出隨蠕變時間的增長，球頭-錐面密封的殘余預緊應力先急劇減小，然后緩慢減少，這與金屬材料的一般蠕變松弛理論是符合的，證明仿真結果是正確的. 實際工程中，當螺母殘余預緊應力降低至其初始預緊應力的60%時，需對螺母重新進行預緊.

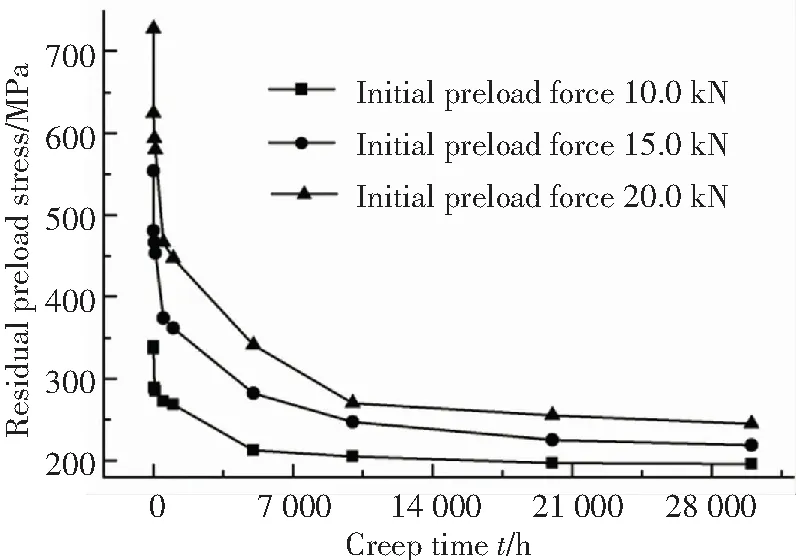
圖6 不同初始預緊力下螺母殘余預緊應力隨蠕變時間的變化

Fig.6 Nut residual preload force change with increasing creep time under different initial preload force

球頭-錐面間接觸應力隨蠕變時間的變化規律如圖7所示，從圖中可以看出隨螺母初始預緊力的增大，對應蠕變時刻下球頭-錐面間的接觸應力會隨之增大，這表明螺母初始預緊力與球頭-錐面間的接觸應力是正相關的. 產生這種現象的原因在于螺母初始預緊力的增大，會使球頭與錐面間產生更大擠壓效應，直接表現為球頭-錐面間接觸應力的增大，這是容易理解的. 從圖中還可以看出，隨蠕變時間的增長，球頭-錐面間的接觸應力會先急劇減小，爾后緩慢減少，這與金屬材料應力松弛理論是一致的. 此外，從圖中還可以看出，不同螺母初始預緊力條件下的，球頭-錐面間的接觸應力均顯著大于流體壓力，表明這一結構及工況下的球頭-錐面密封均滿足密封性能的要求.

與圖7相對應，圖8所示為泄漏率隨時間的變化，從圖中可以看出隨螺母初始預緊力的增大，對應蠕變時刻下球頭-錐面密封的泄漏率會隨之減小. 從圖中還可以看出，隨蠕變時間的增長，3種螺母初始預緊力條件下的泄漏率均會隨之增大，這是容易理解的.

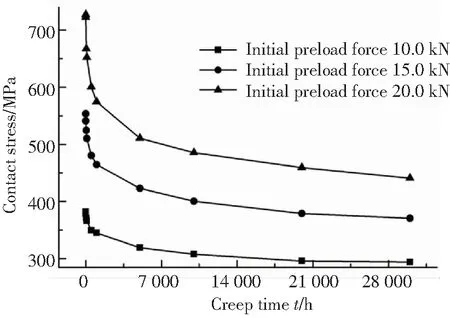
圖7 不同初始預緊力下接觸應力隨蠕變時間的變化

Fig.7 Contact stress change with increasing creep time under different initial preload force

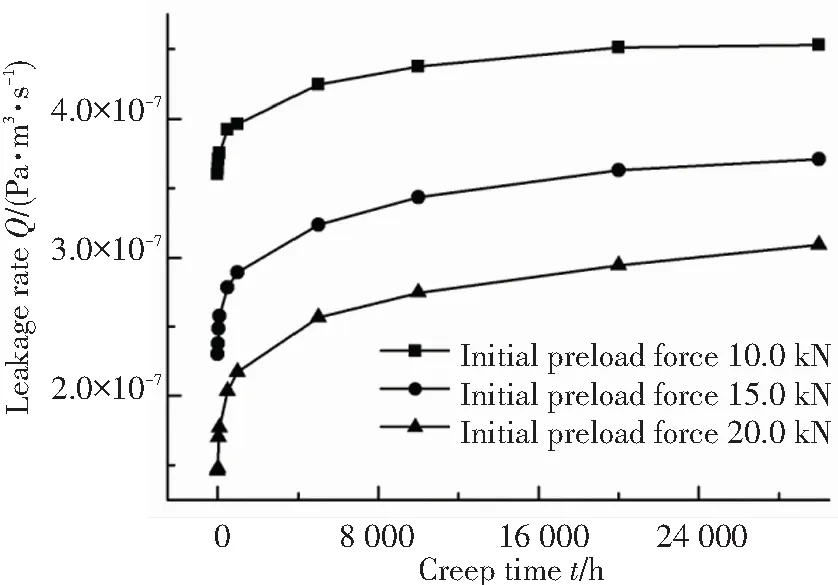
圖8 不同初始預緊力下泄漏率隨蠕變時間的變化

Fig.8 Leakage rate change with increasing creep time under different initial preload force

2.2.2 摩擦系數的影響

摩擦系數對螺母預緊應力及接觸應力的影響如圖9和圖10所示，從圖中可以看出，隨摩擦系數的增大，對應蠕變時刻下螺母的殘余預緊應力會隨之降低，產生這種現象的原因在于：接觸面松弛過程是兩個接觸面間緩慢變形、錯動及相互適應并逐漸擴展接觸面積的過程. 雖然初始預緊力相同，但摩擦系數大，則幾處接觸副接觸面之間初始時接觸得較“虛”，在后期松弛過程中，接觸面間緩慢變形、錯動及相互適應并逐漸擴展接觸面積的過程發生得越容易，所以摩擦系數越大，殘余預緊應力以及接觸應力隨著時間推移下降得越快. 從圖中還可以看出，隨蠕變時間的增長，螺母殘余預緊應力會先急劇減小，爾后緩慢減小，這所呈現的現象是合理的.

圖9 不同摩擦系數下殘余預緊應力隨蠕變時間的變化

Fig.9 Residual preload force change with increasing creep time under different friction coefficient

與圖10相對應，圖11所示為泄漏率隨蠕變時間的變化. 從圖中可以看出，隨摩擦系數的增大，對應蠕變時刻下球頭-錐面密封的泄漏率會隨之增大. 從圖中還可以看出隨蠕變時間的增長，不同摩擦系數下的球頭-錐面密封的泄漏率均會隨之增大.

2.2.3 流體壓力的影響

流體壓力對螺母殘余預緊應力的影響如圖12所示，從圖中可以看出隨流體壓力的增大，對應蠕變時刻下螺母的殘余預緊應力會隨之增大，產生這種現象的原因可能與螺母初始預緊力、接觸面間的摩擦阻力以及流體壓力間復雜的耦合作用有關.

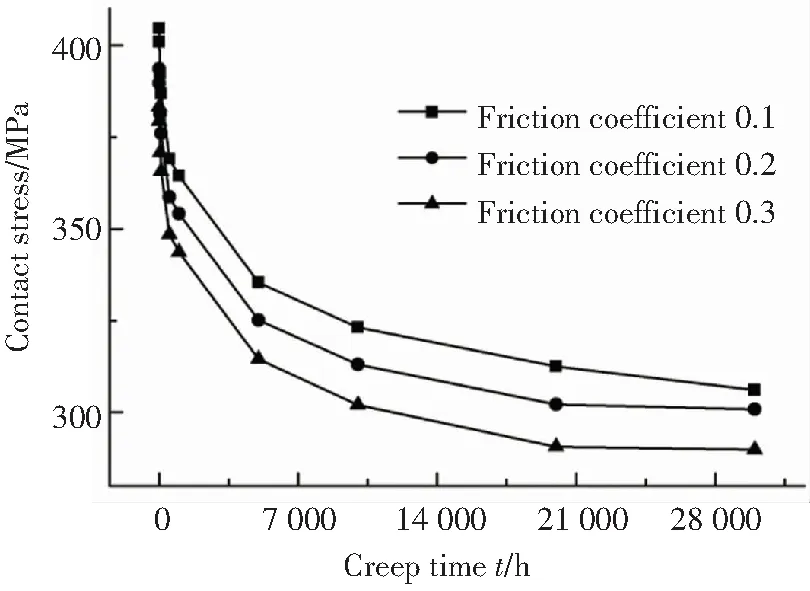
圖10 不同摩擦系數下接觸應力隨蠕變時間的變化

Fig.10 Contact stress change with increasing creep time under different friction coefficient

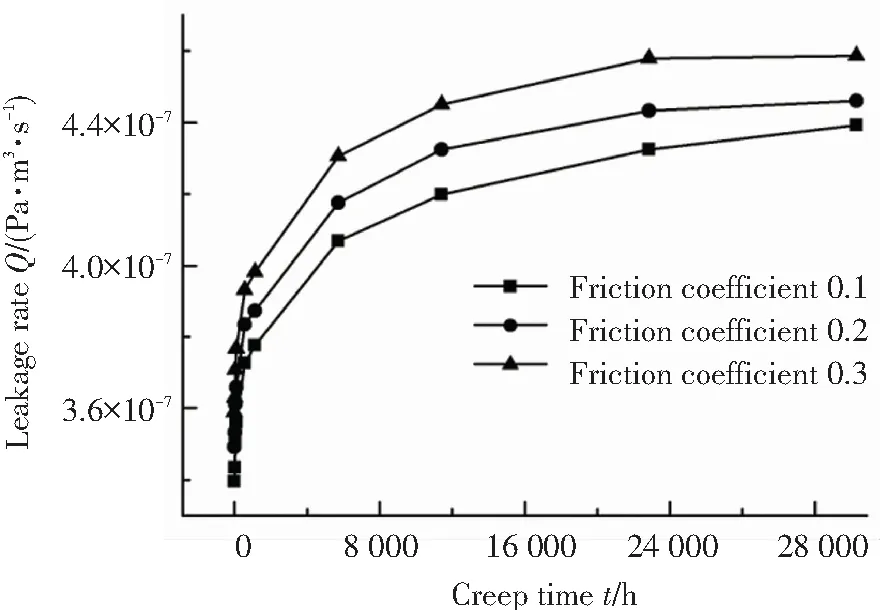
圖11 不同摩擦系數下泄漏率隨蠕變時間的變化

Fig.11 Change of leakage rate with increasing creep time under different friction coefficient

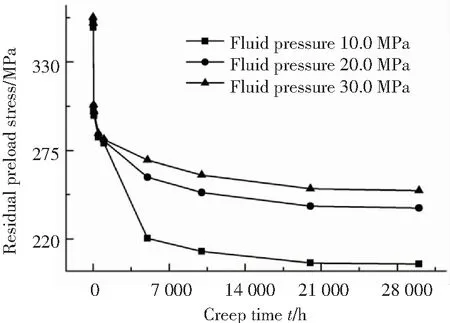
圖12 不同流體壓力下殘余應力隨蠕變時間的變化

Fig.12 Residual preload force change with increasing creep time under different fluid pressure

流體壓力對球頭-錐面間接觸應力的影響如圖13所示，從圖中可以看出隨流體壓力的增大，對應蠕變時刻下球頭-錐面間的接觸應力會隨之略微增大，產生這種現象的主要原因有兩個方面：一是螺母殘余預緊應力與球頭-錐面間的接觸應力正相關，故螺母殘余預緊應力的增大是造成球頭-錐面間接觸應力增大的主要原因之一. 二是在流體壓力的抬升作用下，球頭-錐面間的擠壓效果會隨流體壓力的增大而愈加顯著，這是造成球頭-錐面間接觸應力增大的另一個主要原因.

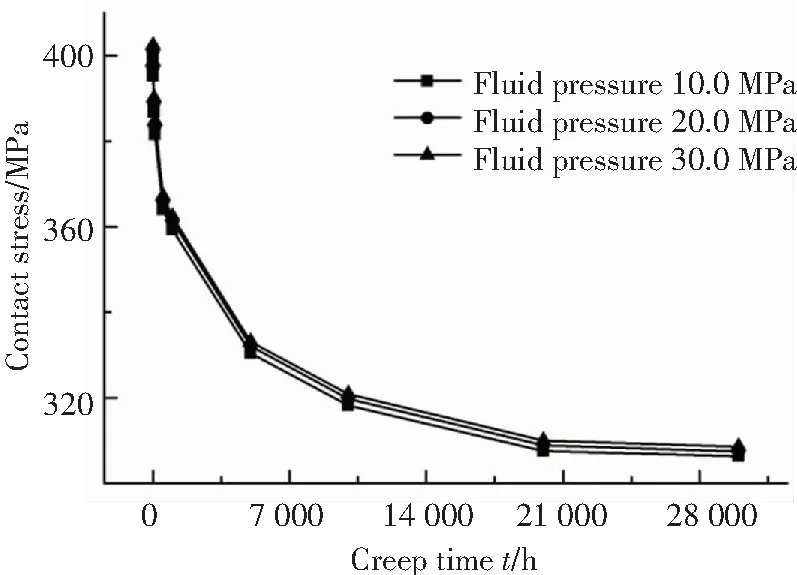
圖13 不同流體壓力下接觸應力隨蠕變時間的變化

Fig.13 Contact stress change with increasing creep time under different fluid pressure

圖14所示為不同流體壓力作用下球頭-錐面密封的泄漏率隨蠕變時間的變化，從圖中可以看出隨流體壓力的增大，對應蠕變時刻下球頭-錐面密封的泄漏率均會隨之增大，這是容易理解的. 從圖中還可以看出隨蠕變時間的增長，3種流體壓力條件下的球頭-錐面密封的泄漏率均會隨之增大，這與圖13所示的現象是相對應的.

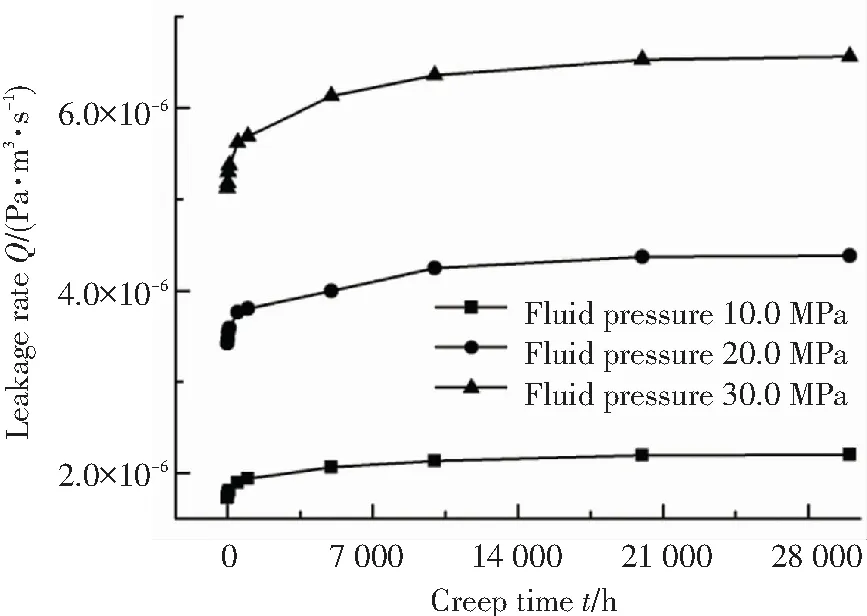
圖14 不同流體壓力下泄漏率隨蠕變時間的變化

Fig.14 Change of leakage rate with increasing creep time under different fluid pressure

2.3 理論結果與試驗結果的對比

參照衛星推進系統工程實際設計了一段管路，其中含有球頭-錐面接點，并對螺母施加預緊力矩. 對管路進行了氦氣充壓，之后管路處于長期保壓狀態，在1年中定期采用氦質譜檢漏儀的吸槍對球頭-錐面的漏率進行漏率測量并記錄了結果. 檢漏的環境條件包括溫度18～28 ℃、相對濕度30%～70%，氣壓為實驗室氣壓，潔凈度優于10萬級.

在錐面傾斜角度β=60°、流體壓力為2 MPa、摩擦系數為0.15及螺母預緊力為10.5 kN條件下，開展考慮應力松弛效應與否的球頭-錐面密封泄漏性能的理論分析及試驗研究. 需要說明的是：試驗中每個蠕變時刻點的泄漏率均需測試3次，然后求和取均值.

圖15 球頭-錐面連接單點檢漏包覆示意圖

球頭-錐面密封泄漏率的理論結果與試驗結果的對比如圖16所示. 從圖中可以看出隨蠕變時間的增長，較之不考慮應力松弛效應和僅考慮球頭-錐面應力松弛，考慮綜合應力松弛效應下獲得的球頭-錐面密封的泄漏率與試驗結果吻合較好. 這表明考慮綜合應力松弛效應下獲得的球頭-錐面密封的泄漏率更加精確. 從圖中還可以看出隨蠕變時間的增長，考慮應力松弛效應的球頭-錐面密封的泄漏率會隨之增大，這與試驗結果所呈現的變化趨勢是一致的，而不考慮應力松弛效應的球頭-錐面密封的泄漏率始終保持不變，這與試驗結果所呈現的變化趨勢存在顯著差異. 這一現象體現出在進行球頭-錐面密封性能分析時，考慮應力松弛效應的影響是很有必要的.

圖16 理論結果與試驗結果的對比

3 結 論

1)對比考慮應力松弛效應與否的球頭-錐面密封性能的差異，研究結果表明隨著蠕變時間的增長，考慮應力松弛效應與否的球頭-錐面密封性能會存在顯著的差異. 這一研究為具有長期服役要求的球頭-錐面密封中多久需要補充螺母初始預緊力提供理論依據.

2)研究螺母初始預緊力對考慮應力松弛效應的球頭-錐面密封性能的影響. 結果表明隨著螺母初始預緊力的增大，螺母的殘余預緊應力及球頭-錐面間的接觸應力均會隨之增大，而其泄漏率會隨之減小，這表明螺母初始預緊力的增大會提升球頭-錐面密封的性能，但值得注意的是，過大的螺母初始預緊力，可能會對球頭-錐面密封結構的實際使用壽命產生不利影響. 因此，在滿足密封性能的基礎上，選擇較小的螺母初始預緊力是很有裨益的.

3)探討摩擦系數對考慮應力松弛效應的球頭-錐面密封性能的影響. 結果表明隨著摩擦系數的增大，螺母的殘余預緊應力及球頭-錐面間的接觸應力均會隨之減小，而其泄漏率會隨之增大，這與不同粗糙度下，表面實際接觸區域及接觸狀態存在差異有關. 因此，提高加工表面的質量，可以有效提升球頭-錐面密封的性能.

4)分析流體壓力對考慮應力松弛效應的球頭-錐面密封性能的影響. 研究結果表明隨著流體壓力的增大，螺母的殘余預緊應力及泄漏率均會顯著增大，而球頭-錐面間的接觸壓力會略微增大. 這一研究為超高壓流體作用下，螺母初始預緊力等的選取提供理論依據.

5)開展考慮應力松弛效應與否條件下獲得的球頭-錐面密封的泄漏率與試驗結果的對比. 研究結果表明，較之不考慮應力松弛效應，考慮應力松弛效應下獲得的球頭-錐面密封的泄漏率與試驗結果吻合較好，體現出在開展球頭-錐面密封性能分析時，考慮應力松弛效應的影響是很有必要的.