讓數學知識自然生長

王衛霞

摘 要：眾所周知，在教學過程中創設一定的現實情境，可以幫助學生體驗生活經驗，激發學生學習的熱情，對學生的學習有積極的意義。但是在具體實施的過程中，創設情境有時會走向極端，甚至到了“無情境不數學”的地步，出現為了情境而情境的現象，這樣的數學課雖然表面上熱鬧了，但是卻缺少了數學本身的趣味，背離了創設情境為教學服務的理念。根據數學學科本身的特點，采取“舉一反三”“數形結合”等方法，使數學利用自身的力量又好又快地自然生長。

關鍵詞：核心知識;知識聯系;舉一反三;數形結合

奧蘇貝爾認為：“影響學習的最重要的因素是學生已經知道了什么，我們應當根據學生原有的知識狀況去進行教學。”現在不少數學課尤其是公開課都遵循情境教學的理念，為學習創設生動有趣的情境。這些情境在一定程度上對激發學生的學習興趣有積極的作用。但是筆者認為，激發興趣單純依賴創設情境是遠遠不夠的。數學知識之間有其獨有的內在邏輯關系，如果不遵循客觀規律而人為地去創設一些情境，那樣課堂雖然熱鬧了，但缺少了知識增長的自然感和連續感，不利于學生的長遠發展。本文試圖從數學知識的內在聯系出發，找準數學知識的生長點，幫助學生提高數學學習的速度和質量，用數學本身的魅力來打動和吸引學生，構建自然生長的數學課堂，從而進一步提升教學質量。

一、依靠核心知識，促進學生舉一反三

許多學習數學存在障礙的學生認為，數學學科知識點眾多，學習起來困難很大。其實在眾多的知識點中，有些知識點處在最基礎、最核心的地位，它們的作用就像植物的種子一樣。牢固掌握了這些“知識種子”，學生的數學知識和技能才能發芽生長，如果這些知識掌握不好，影響了種子的質量，那么學生的數學學習將會受到很大的影響。例如：在方程的知識體系中，“等式的性質”就是知識的關鍵。理解掌握了等式的性質，我們可以很容易地解答一步計算的方程，繼而可以把形如ax±b=c的兩步計算的方程通過等式的性質轉化成一步計算的方程來計算，起到舉一反三、融會貫通的作用。

“一生二，二生三，三生萬物。”數學知識也是由處于核心地位的知識慢慢擴展、生長，最后形成整個數學生態體系。對于這些核心的知識，我們應該抱著怎樣的態度呢？

有的觀點側重于機械傳授，即強調“間接經驗”的傳授，教學方式僵化，甚至依靠學生死記硬背。如少數老師為了提高學生計算的正確率，要求學生將圓周率的近似值“3.14”與“1～100”相乘所得的積背下來，這是一個非常艱巨的任務，這種“高投入，低產出”的粗放式學習方式雖然對學生短期成績的提高有一定的幫助，但是這種機械做法會扼殺學生學習數學的興趣，從學生的長遠發展來看“弊”遠遠大于“利”，其效果無異于“殺雞取卵”。

有的觀點強調學生直接經驗的獲取，認為數學課堂上如果沒有采用新理念所倡導的“探究性學習”和“小組合作學習”，就必然是一節失敗的課。這種學習方式突出了學生的“主體地位”，對培養學生分析、解決問題的能力有著極其重要的作用。但是知識浩如煙海，如果“事必親躬”，走向極端，必定會極大地影響學習效率。

以上兩種觀點都是極端和片面的。隨著課程改革的推進，融合了“接受學習”與“合作學習”優點的“有意義的接受”與“強調學生的主體參與”并重的做法越來越受到人們的重視。這種做法既重視對知識的接受學習，又突出學生的主體地位，發展學生的獨立思考能力，引導學生結合自身的實踐和經驗對數學知識進行再加工，從而促進學生知識和技能的全面提升。

二、注重聯系比較，滋潤知識自然生長

數學知識之間有著緊密的聯系，幫助學生把握知識發展的脈絡，有助于學生建構可持續的知識發展體系，形成堅實的知識之網。

1.注重知識的橫向聯系

教師在教學中引導學生關注數學知識之間的橫向聯系，有利于學生對所學知識進行比較分析，從而發現知識之間的相似之處，利用學習舊知的成功經驗來作為學習新知的鋪墊，有助于新知的理解和同化。

在教學異分母分數的加法和減法時，一定會涉及分數單位的概念。異分母分數相加減的一個必要的過程就是將異分母分數利用通分轉化成同分母分數，這樣，分數的計數單位就由不同變為相同了。為什么要經歷這樣的過程呢？部分學生可能會感到不解。教師在教學時可以引導學生展開橫向的聯想：分數單位也是一種計數單位，類似于整數的計數單位“個、十、百”等。聯系以前整數、小數相加減的知識學生就會明白：整數相加減時把末位對齊，是為了使相同的數位對齊;計算小數相加減時將小數點對齊，目的同樣是使得兩個數的“個位和個位”“十分位和十分位”等相同的數位對齊。通過聯系和比較，學生就會從已經熟知的數學知識中找到新知識的生長點，新知的理解和接受會更加自然。

2.重視知識的縱向聯系

學生的數學學習過程是一個由淺入深、循序漸進的過程，教學中注意引導學生關注知識之間的縱向聯系，使學生從舊知中發掘新知的增長點，這正是“溫故而知新”的價值所在。

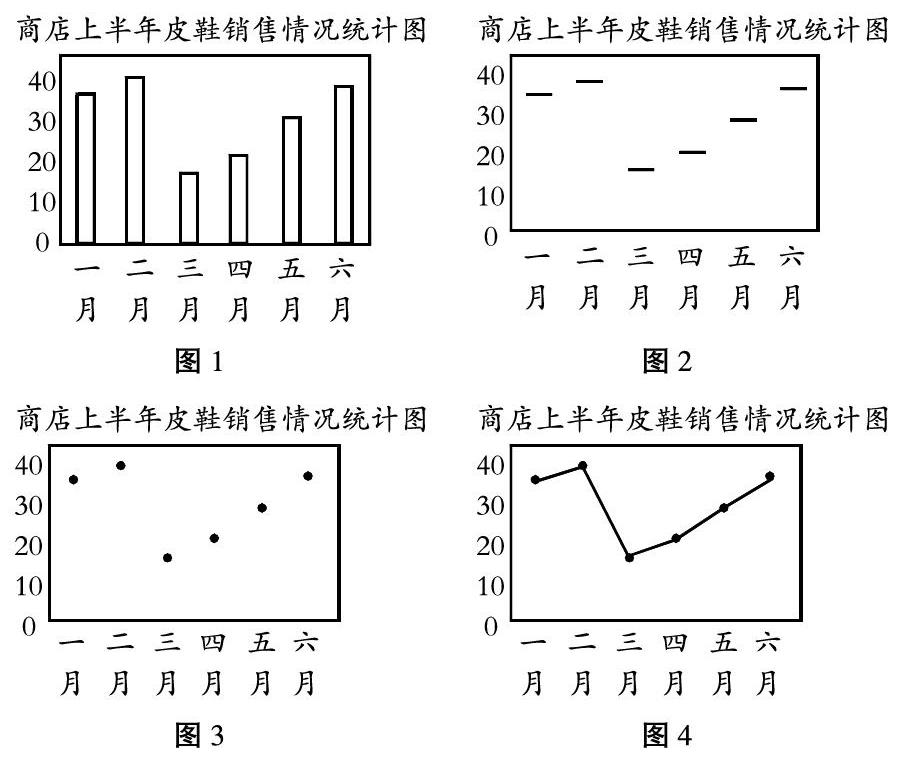
在概率與統計部分，學生依次會學習到條形統計圖和折線統計圖的有關知識。新課程標準要求學生能夠根據題目中的數據繪制出相應的統計圖。眾所周知，條形統計圖是利用條形的高度來表示數量的多少，而折線統計圖是由一個個的點連接而成的，它是利用點到橫軸間的距離的長短來表示數據的多少，從這一點來說，折線統計圖與條形統計圖之間有著密切的聯系。如果學生對條形統計圖的相關知識學得很好，會對折線統計圖的掌握起到良好的促進作用。在教學折線統計圖時，可以預先對學生已經學過的條形統計圖（如圖1）進行復習，然后將條形的隱去，只保留標志數量多少的上面一小塊（如圖2）。

這時就可以看成了一個個表示數據的“點”（如圖3），然后連點成線，就變成了我們所要學習的折線統計圖的新知識（如圖4）。這種做法將新知識的學習和學生已有的知識基礎緊密聯系在一起，不僅可以打消學生對新知的陌生感，還可以使學生利用已有的知識經驗加深對新知的理解，促進學生對新知的掌握。

三、運用幾何直觀，促進思維跨界聯姻

在“數”與“形”的關系中，“數”側重于抽象邏輯思維，“形”側重于具體形象思維。小學階段正是學生的思維從具體形象思維向抽象邏輯思維的過渡時期。如果教師在課堂上能夠將“數”與“形”巧妙地結合起來，不僅可以使學生的多種思維能力得到有效的訓練，而且由于多種思維優勢互補，對學生掌握數學知識能夠起到出奇制勝的效果。

我國著名的數學家華羅庚曾用一首詩來形容數與形的關系：“數缺形時少直觀，形少數時難入微;數形結合百般好，隔離分家萬事休。”這首詩很好地說明了“數形結合”的巨大作用。

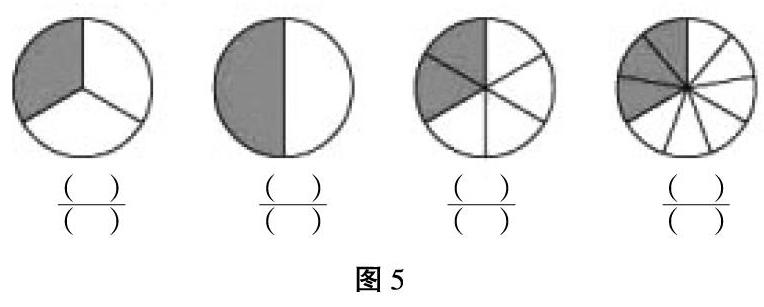
例如，在學習“分數的基本性質”時可以設置下圖（如圖5）。圖中有四個大小相同的圓，分別被平均分成了若干份，用陰影部分表示了其中的相應部分。其中第一個圖用分數表示為三分之一，第二個圖為二分之一，第三個圖為六分之二，第四個圖為九分之三。學生依靠觀察可以判斷出第一幅圖與第三、第四幅圖形的陰影部分面積相等，從而得出對分數的基本性質的直觀感知。有了直觀形象的支撐，教學效果要比單純的“就數論數”要自然得多。

同樣的，我們在研究“形”的時候可不可以讓“數”來幫忙呢？答案是肯定的，比如我們在學習相鄰體積單位之間的進率時，可以設計這樣的插圖（如圖6）：

左邊是1個大正方體，右邊是1000個小正方體。左邊大正方體的體積是1立方分米，右邊一個小正方體的體積是1立方厘米。這樣的意圖是讓學生通過比較左、右兩個正方體中單位正方體的個數，從而明白“1立方分米=1000立方厘米”。在實際的教學過程中，學生對于右邊這個圖形中的小正方體的個數估算缺乏經驗，加之學生對于較大的數目還沒有比較準確的體驗，因此盡管老師一再強調要學生認真觀察，但是還是有很多學生不敢相信右邊這個正方體中居然包含1000個小正方體，影響了教學目標的達成。在這種情況下，借助于“數”的力量就可以有效解決這個問題。教師可以在正方體相交于同一個頂點的三條棱上分別標出正方體的棱長是多少，左邊正方體的棱長以分米作單位，右邊的棱長以厘米作單位。右邊的一個小正方體的棱長是1厘米，體積為1×1×1=1立方厘米。最下面一層包含有“10×10=100個”這樣的小正方體，一共有10層，也就是1000個。因為左邊的正方體的體積是1立方分米，而且左右兩個正方體的體積同樣大，可以很輕松地得出立方分米與立方厘米之間的進率為1000。借助“數”的參與，能夠幫助學生將本來比較模糊的概念變得清晰“入微”。

數學課堂應當是富含生命活力和張力的課堂，是知識自然生長的課堂。我們要充分發揮學生學習的主體性、激發學生學習的熱情、注重知識的聯系和發展、促進思維的融合與提高，這樣我們的數學課堂才會走上可持續發展的道路，真正達成負擔輕、效率高、質量好的理想的教育目標。

編輯 李 爭