采光口光強體數學模型

羅茂羲, 鐘祖勛, 羅 奕

(重慶大學 建筑城規學院, 重慶 400044)

天然光是取之不盡、用之不竭的綠色能源，被廣泛引入人類的活動場所，用于發電、取暖，也為人類創造生活、學習、工作的光環境。長期以來，世界各國為了更好地利用天然光，根據各地域的光氣候特點，結合國民經濟發展及民族的生活習慣，研究制訂了適合國情的天然采光設計標準（規范或指南）。例如，國際照明委員會（CIE）1967年根據澳大利亞“采光計算國際建議”修訂的計算方法，中國的《工業企業建筑采光設計標準》（TJ 33—79），前蘇聯的達尼留克圖表法，美國的光能量法（利用系數法）等。這些不同的采光設計計算方法，體現了天然采光設計和計算的多樣性。科學家根據自己的研究成果，為天然光的利用作出了巨大貢獻，但卻不易比較，計算難度較大。

縱觀各種方法，人工照明的利用系數法相對比較容易實施。如果把采光口視為在“臨界照度”時的一個燈具，就可以尋求一種同樣的計算方法完成設計計算工作。為人類創造的都是同一個光環境，在滿足人眼需求的感覺量前提下，僅僅是光能量的多少和光譜組成的差異。

人工光源在一天中很穩定，但天然光不同。早上和中午，室外照度相差極大，陰天和晴天的同一時刻室外照度亦相差很大。天然光，在一天中是一個不穩定的光源，故設定采光場的光環境剛好滿足人的視覺工作需要，則稱此時無遮擋天穹散射光水平照度為“臨界照度”。“臨界照度”的設定因各國國情和地域的光氣候不同而異，為研究方便，設定“臨界照度”為1×104lx。

“臨界照度”下，在不同結構、不同材料、不同外界光源的作用下，同一個采光口會有多個光強體形態存在，都可以用數學公式表述。人工燈具的光強度（光強體）也可以用數學模型表示，因此，可以用同樣的方法（區域光效法）計算照度。

1 采光口

根據功能的要求，以及地域和緯度的差異，可設置不同形狀的采光口。由于建筑物圍護結構的限制和采光的特殊要求，常用的采光口分為三大類：1）豎向采光口。矩形采光口、等邊三角形采光口、圓形采光口；2）水平采光口（屋頂頃角小的采光口）。矩形采光口、圓形采光口；3）復合型采光口。縱向和橫向天窗、鋸齒形天窗、井式天窗。

2 采光口外亮度源

采光口是采光空間收集天然光的通道，其收集的光能來自窗外的發光體和反光體。凡是給采光口輸送光能的有光物體都是采光口的光源。對采光口而言，被天然光照亮的大地、近物和遠山，都是采光口的光源。采光口外不同的區域和亮度的不同，造成采光口內側光分布的差異和采光效果的差異。

2.1 天穹亮度分布

地球大氣層被太陽光照射，就變成了一個有光的球殼。對地球上處于白天的所有區域而言，這個亮殼是隨太陽位置不同而變化的。只有在全云天時，即天空被10級云覆蓋時，天空亮度分布才是相對穩定的，近似于蒙·斯本塞（Moon·Spencer）提出的全云天天空亮度分布式，即：

也可用式（1）表示。

式中，Lγ為高度角γ的天空亮度值，亮度單位cd/cm2或cd/m2。

因此，在全云天時，根據立體角投影定律，在“臨界照度”為10 000 lx時，天頂亮度LZ為

設定“臨界照度”E0=10 000 lx時，全云天天空亮度分布見式（2）。

若是等亮度天空，則天穹亮度Lc= 3 183.1 cd/m2。

2.2 地穹亮度分布

水平采光口，絕大部分的入射光來自天空。對于豎向采光口，除了天空的入射光外，還有窗外的地穹反射光。地穹反射光的強弱有兩個主要因素：一是天穹的亮度；二是地物的反光能力，草地、黃土、綠地大不相同。地物亮度場是由眾多物體表面反射光構成的綜合效果，將部分反射光通過采光口投入采光空間內，對采光有貢獻，類似于一個天穹，這里簡稱地穹，與天穹對應，是高度角γ=0°的水平面，即分界面。

2.2.1 地穹反光系數

2.2.2 地面照度計算式

采光口外地面上各點，受設窗建筑物自身的遮擋，在同一時刻所接收的天然光各不相同，即各點的照度不同，如圖1所示。沿采光口的x軸垂直面方向，在地面上設點1～n，n點為無窮遠點。從采光口坐標原點o，至各點的俯角γ，依次為

在亮度為Lγ的天空中，在天穹球面取一微元dS，見圖1（ b），則有在xoy坐標面上的投影

因此，微元dS以球心o點為頂點構成的立體角

根據天然采光的立體角投影定律，天穹亮度Lγ、微元dS對地面xoy上建立的水平照度

式（3）的積分域

2.2.3 采光口外地面照度

見圖1（a），窗外地面各點的照度，受設窗建筑物自身的擋光所影響，在同一時刻，都比無遮擋的水平照度低。窗外各點的俯角γ，也是各點至坐標原點o的仰角，則各點的垂直遮擋γ和水平遮擋α如表1所示。

將式（1）Lγ代入式（3）則有各點照度值Ei

2.2.4 地穹亮度分布

室外地穹表面按均勻擴散面處理，則地面照度和亮度關系為

表1 各點的垂直遮擋和水平遮擋

式（4）中的地面綜合反射系數ρd，根據地域室雪外的具體狀態取相應值。將上面1～n點的窗外各點照度值代入式（4），則有室外地面各點的亮度：

圖2為一近似橢圓曲線段，在離采光口較遠的扇形地穹亮度分布可用式（5）表示。

式（5）中Ld適用范圍是窗前地穹扇形區域。

ρd是地穹的綜合反射系數，根據地域環境設定和代入。還有衍生亮度源：遠山亮度Lh和近物亮度Lh。

Lh在全云天天空下的垂直面照度見圖3，有式（7）存在。

式中： “－”號表示照度矢量指向y軸負向，4 092.6 lx是無遮擋的垂直面照度值。

3 結構厚度對采光口采光影響

建筑物護圍結構的厚度d對任何采光口的采光都有影響，尤其是窗面小的采光口。d所影響的區域，是計算點M在窗平面上的投影，落在窗面外時，特別是M點接近窗平面區域時，尤為嚴重，照度（光強度）值為0。

3.1 墻的厚度對豎向采光口的采光影響

墻的厚度就是豎向采光口的厚度d。采光口的d尺寸對采光影響大，特別是當計算點M的正投影點落在窗洞外的區域時，從M點見到的窗洞面積，由于窗框的遮擋而縮小，則M點的照度值（光強值）比理論值小。在豎向窗中，OM靠近yoz坐標平面時，當M點處不能直視窗外光源時，則M方向的照度為零，當然光強度也為零，見圖4。當M點在yoz坐標平面上的投影點在窗框外時，由于d的存在，采光面會出現 Δy和Δz陰影區。對測點M而言，這是被窗框遮擋的采光面積。在計算M點的照度時，應減掉陰影區的面積，實際上是減光源投射到M點的光能，這個陰影區因M點位置改變而變。故需要尋找陰影區與α0、β0、γ0的關系，即尋求M點與陰影間的數學表述式。

M點是采光口內側半球面上的測點，M在yoz坐標面上的投影O'，r是坐標原點o至M測點的距離，取r=10～100 m。

被d遮擋的面積

采光口的有效面積

r＞＞b、c、d（窗口尺寸），當r＞4b，r＞4c時，采光口可按點光源對待。或者，采光口的有效面積用下式表示：

上式S有雙重含意：1）隨測定M的位置不同而變化；2）轉換為采光口光強度數學模型的修正系數K。

豎向矩形采光口：

豎向三角形采光口：

豎向圓形采光口：

三式中，α0、β0、γ0是計算（測試）點M的OM至x、y、z坐標正向間的夾角，（ °）；

r是OM的長度，m；

b、c、d、h、R是采光口的結構尺寸，m。

3.2 屋頂厚度對水平采光口的采光影響

屋頂厚度設定為d。與豎向采光口類似，d的存在，對窗的采光同樣有很大的影響。當測點M的投影點落到水平采光口平面外的區域時，從M點見到的窗洞面積，因窗框遮擋而縮小，即M測點靠近水平采光口坐標平面時，球面上的M點受光為零。見圖5，陰影區是M點在坐標位置時，窗面被窗框遮擋的區域。在計算水平采光口光強度時，消去陰影對M點形成的立體角，即抹掉陰影區被遮擋的入射光，使采光口在OM方向有更精準的光強度。

陰影的面積，與M點的位置密切相關，設定r為10～100 m。

被窗框遮擋的陰影面積

水平采光口的有效面積

同理，有水平采光口光強度修正系數K。

矩形水平采光口光強度修正系數

水平圓形采光口光強度修正系數

修正系數K的作用是削去采光口內半球面上各點M因采光口結構厚度d的存在而減少的光能。

3.3 采光口透光結構對采光的影響

采光口透光材料可以有多種選擇，各種不同的透光材料，透光系數各不相同，而且透光材料的光線分布范圍也不同。如圖6所示，(a)、(b)、(c)、(d)分別為無色透明平板玻璃、磨砂玻璃、半透明玻璃、乳白玻璃（均勻擴散透光材料）。入射角相同的幾束光，照射不同的透光材料，在透光側不但I0不等值，而且I0與法線的夾角也不等，夾角縮小，光的分布范圍擴大，直至均勻擴散。因此，用不同的透光材料，室內采光效果也不同，通過窗口觀看室外景物亦大不相同。

I0＜Iα，I0與透光材料的擴散能力和透光系數有關，α≥α｀，材料的擴散能越大，α｀越小。從定向透射到均勻擴散，α≥α｀之間構成有序的規律。

定向透射：

若光束Iα投射到O點的光能為F，則在均勻擴散透光材料的透光面（透過的光τF在半球面均勻分布）有I0存在：

按“朗伯余弦定律”，可以表述透光面的光分布

采用均勻擴散透光材料的采光口，只需要應用式（3）立體角定律求水平采光口照度，應用式（7）立體角投影定律求豎向采光口窗面的照度，然后再用式（13）繪制采光口內側的光強體圖，式（13）中：

S為采光口的有效面積，m2。

主要研究無色透明的平板玻璃結構的采光窗，采光口的透光結構對窗的采光效果影響很大，木格結構、金屬結構的透光效果不同。根據相關資料估算，窗結構透光系數，豎向窗τw=0.4～0.6，水平窗τw=0.25～0.4。大致可以表示窗的采光能力。

研究窗內側的光分布數學模型，τw待定。數學式所描述的光強體模型，是指室外“臨界照度”為1×104lx時的特定條件下，窗內側的光分布狀態。無色透明的平板玻璃反光系數很低，ρw=0.10。

只研究采光口光源為天穹光和地穹光的情況，不計Ln、Lh衍生光源的作用。

4 采光口外光源作用區

窗外有地面和天空，以xoy坐標面為界面，分別稱為地穹和天穹，如圖7 所示。地穹因天穹發光而有光，是一衍生光源。地穹區、天穹區的亮度分布，見式（5）Ld和式（1）Lγ。

在豎窗中，天穹光作用區在窗內側的下半球區域，地穹光作用的是上半球區域，當然I1＞I2。在水平窗中，地穹光的作用不大，主要是天穹光，光的作用區在天窗的內側半球面。當然，斜屋頂上的天窗又當別論。

5 光源、采光口、照度、光強度

光源L的光能F，是通過采光口到達被照點的，所以在觀察點M處可以看到采光口外的光源，而且在窗口內側半球區域內，都可以看到光源的存在。以天穹為例，采光口內側窗洞替代了天穹的位置，把天穹全云天亮度變化印在采光口窗面上，為研究窗洞的光分布提供了方便。地穹亮度的光源，亦可如此處理。

照度因采光口和亮度源L的存在而存在，如圖8所示。

面光源對被照點M處鑄造的照度，依據立體角投影定律來確定：

點光源在I方向垂面上的M點鑄造的照度值

因此，對被照面而言，入射光能的方向不同，所獲得光源光能的量也有區別。

為獲得采光口面光源，有如人工照明燈具一樣的光強體，把窗內側半球面計算（測試）照度E的距離r增大，使r大于采光口尺寸4倍以上。則該窗口可按點光源對待。取r=10～100 m。根據上兩式，則有采光口坐標源點O至測點M方向的光強度，按式（15）計定

因此，把面光源在OM方向M點的照度值，轉變為OM方向的光強度值。這樣窗戶的光強體存在和繪制就有了依據。

6 采光口光強度積分原式

6.1 豎向采光口光強度積分原式

天然光透過豎向采光口投入被照場內，在采光口內側半球面方向構成一光強體。該光強體的形狀、大小，與天穹亮度和亮度分布，與其他亮度源的分布，與采光口的有效透光系數及光學性質有關。

如圖9所示，設x、y、z坐標原點O與采光口的形心重合。采光口的光強度始點為坐標原點O，命計算點M在采光口內側方向，以坐標原點O為球心，r為半徑的球面上。則在采光口外各亮度源的作用下，在采光口透光面OM方向上，有光強度矢量dIM存在。

如圖9，設OM的光強度dIM矢量與坐標x、y、z正向間的夾角依次為α0、β0、γ0，則有

已知O'點是M點（空間點）在yoz坐標平面上的投影點，W是O'U與SF的交點，如圖9所示，則有軸MU⊥z，MW⊥SF。把計算點M設在以O為圓心，r為半徑的球面上，OM=r。

則根據各點坐標有dS在SM方向的投影參數，見圖9。

dS在M點的立體角dΩ，在OM方向的投影參數

天穹亮度源Lγ(dS)的sinγ參數

地穹亮度源參數

以上，以α0、β0、γ0標定M點（即OM）在窗內側半球面上的空間位置。以α0、βx表示M點的空間位置。βx是yoz坐標平面內，與oy正向間的夾角，區間0→2π。因此，用βx和α0表示IM的方向。βx值見圖9。βx值是豎向采光口計算光能量的必要參數。

式（16）至（20）中：

γ是亮度源dS的高度角，（ °），天穹地穹

α0、β0、γ0是OM矢量與坐標x、y、z正向間的夾角，（ °）；

βx是OO｀矢量在yoz平面，反時針轉與y軸正向間的夾角，（ °）。

矢量SM（即dIs）在OM(即dIM)方向上的投影（分矢量）

為求OM方向M點的照度（光強度），需借用立體角投影定律，見圖9，即把位于采光口上的dS微元，與天穹地穹對M點構成的立體角dΩ連成一體，即LdΩ，根據立體角投影定律，首先使dS斜面（投影）轉為垂直于SM的垂面，見（16）式，再比SM2，即獲dS對M為頂點的立體角

SM方向M點的照度dES=LdΩcosθ，此時cosθ=1，則

代入（21）式，有dES在OM方向的分量

在式（8）至式（10）中，表示M點在該位置時，因結構厚度d的存在，豎窗采光面被遮擋后剩下的有效采光面積S，轉換為修正系數K，代入上式中，并考慮采光口透光結構的透光效率τW。同時約定采光口的最大尺寸，小于OM（窗內側半球面半徑）的1/4時，根據式（15）和（21）,該窗面光源（采光口）近似點光源。查式（15），則有豎向采光口在OM方向，把上式dE值轉換為光強度值。故有豎向采光口光強度積分原式

也可以從另一途徑尋求OM方向的光強度IM。

LdS是一漫射光源，在SM方向的半球面內，釋放的光能為

dF在SM方向有矢量

將dI0代入式（21），在OM方向的光強度分量

故有豎向采光口光強度積分原式

在式（22）中：

b、c、d為窗結構尺寸，m；

τW是采光口透光結構透光系數，τW=0.4～0.6；

IM是OM方向的光強度，cd；

r是采光口內側半球面半徑，m；

E是半球面上M點的照度，lx；

L是高度角為γ處的采光口外亮度源dS的亮度，cd/m2，L可以是常數或函數；

α0、β0、γ0依次是OM與坐標系O-x、y、z軸正向間的夾角，（ °）；

K是光強度修正系數，是由M點對應的豎向采光口有效窗面積轉換而來，是隨M點游動的變量。

6.2 水平采光口光強度積分原式

水平采光口的亮度源，主要是天穹L采光口亮度微元dS（dxdy），球面計算點M。三點在同一直線時，亮度源L的光能通過dS在SM方向，有一光強度矢量dIS。dIS在OM方向有相對應的光強度分量dIm。則采光口在OM的總光強度Im可求。

如圖10所示，OM方向矢量與坐標O-x、y、z軸正向間的夾角，依次為α0、β0、γ0，并有下列等式存在。OM在xoy平面上投影OO'。OO'從x軸正向始，在xoy平面內，反時針繞z軸轉，有αz角存在，范圍0～2π。γ0和αz表示OM的空間坐標。

在圖10中，O｀是M在xoy采光口平面上的投影點，故有SF⊥Ox，SF⊥O'U，SO'⊥O'M，O'M⊥O'U，SW//y，O'U//x ，SW⊥MW。

根據各點坐標有dS在SM方向的投影參數，見圖10。

dS對M點的立體角dΩ，在OM方向的投影參數

亮度源參數

地穹亮度源參數

式（23）～式（26）中：γ為亮度源dS的高度角，（ °）；α0、β0、γ0是OM矢量與坐標O-x、y、z軸正向間的夾角，（ °）；αz值見圖10。αz角在x軸正向xoy坐標平面內，反時針繞z軸旋轉，范圍0～2π。αz值是水平采光口光能量計算的必要參數。

矢量dIS（SM）在OM（dIM）方向上的分矢量

與豎向采光口類似，有水平采光口在OM方向的光強度IM積分原式

式中（29）：τW為窗口透光結構透光系數，τW=0.25～0.4；a、b、d為窗結構尺寸，m；IM為窗口在OM方向的光強度，cd；r為窗內側半球面半徑，m；E為窗內側半球面上M點的照度，lx；L為高度角γ的采光口外亮度源dS的亮度，cd/m2，L可以是常數或函數；α0、β0、γ0為光強度IM矢量與坐標O-x、y、z系軸正向間的夾角，（ °）；K是光強度修正系數，由M點對應的水平采光口有效窗面積轉換而來，是隨M點游動的變量。

7 豎向采光口光強體數學模型

7.1 豎向矩形類采光口光強體數學模型

在研究采光口的配光時，設定測點M到坐標原點O的距離（半球面半徑）r≥10 m。此時，若窗口尺寸b、c、d小于r的1/4，M點的照度（光強度）誤差較小，窗口面光源可以按點光源對待；若窗口尺寸較大，則根據窗結構分解為多個采光口計算。以下是戶外亮度源作用下，豎向矩形類采光口的光強體數學模型。

只有天穹光、地穹光作用下的豎向矩形類采光口光強體數學模型。將“臨界照度”時的天穹亮度Lγ、地穹亮度分布Ld、墻厚d的影響，以及采光口的相關參數代入（22）原式。見圖11，豎向矩形類采光口內側光分布，由兩部分合成，即天然光Lγ作用曲線I1，地穹光Ld作用曲線I2。

將積分域D、τw、式（8）K值等相關參數代入（22）原式，則有豎向矩形采光口的光強體數學模型

完成（30）式積分后，再代入α0，β0，γ0各參數。

則可計算和繪制此豎向矩形類采光口光強體圖。

7.2 豎向等腰三角形類采光口光強體數學模型

三角形采光口大小，可以按點光源處理，見圖12。若只有天穹光和地穹光作用，其內側光分布與圖11類似。豎向等腰三角形類采光口的光強體數學模型有

將以上豎向等腰三角形積分域及K值等相關參數代入式（30），替換矩形參數，或代入（22）原式，則有豎向等腰三角形類采光口在天穹光Lγ和地穹光Ld作用下的光強體數學模型。

7.3 豎向圓形類采光口光強體數學模型

豎向圓形類采光口的光強體數學模型，與矩形類采光口的模型，僅僅是積分域和K不同，所以把圓形類采光口的相關參數代入式（30），替換矩形采光口的參數即可，并代入式（10）d相關的光強度修正系數K，也可將各參數代入（22）原式。

豎向圓形類采光口見圖13，當體量可以按點光源處理時，在天穹光Lγ和地穹光Ld的作用下，其內側光分布與圖11相似。

豎向圓形類采光口（見圖13），其邊界條件：

將圓形類采光口積分域和式（10）的K，代入式（30），替換豎向矩形類采光口的相關參數，則豎向圓形類采光口在天穹光Lγ和地穹光Ld的作用下，則有豎向圓形類采光口的光強體數學模型，也可將相關參數代入式（22）獲得結果。

8 水平采光口光強體數學模型

8.1 水平矩形類采光口光強體數學模型

研究水平采光口的配光見圖14，設定測點M至坐標原點O的距離r≥10 m，使窗口尺寸a、b、d小于r的1/4，則M點的照度（光強度）誤差較小，窗口可按點光源對待，則有式（15）的關系存在。當采光口的縱向尺寸或橫向尺寸很大時，可以將其分成多個窗口計算。

水平采光口，窗外主要光源是天穹光Lγ，但也可能出現擋光的插入光源。以下研究水平矩形類采光口的光強體模型。只有天穹光作用下的水平矩形類采光口內側光分布，如圖14所示。

對水平窗口而言，Lγ是繞z軸對稱分布的。將式（11）d有關的光強度修正系數K，式（25）sinγ代入式（1），窗口的邊界參數a、b、d全部代入式（29），則有水平矩形類采光口，在10 000 lx“臨界照度”時的光強體數學模型

完成上式積分后，再代入α0、β0、γ0各參量

則可計算和繪制此類水平矩形類采光口的光強體圖。

8.2 水平圓形類采光口光強體數學模型

水平圓形類采光口，這里只記天穹光Lγ的作用，與水平矩形類采光口的不同點是積分區域有別，當然配光也有區別，與圖15相似。

將式（12）d相關的光強度修正系數K、邊界參數代入式（33），替換矩形類采光口的參數，則有水平圓形類采光口的光強體數學模型，也可將相關參數代入式（29）獲得結果。

8.3 水平采光口與屋面傾角

在工業廠房中，平屋面較少，在單層廠房中，因排雨雪的需求，常常設置傾斜α角的屋面。在亮度均勻（Lc）的天穹下，對采光口的配光沒有大的影響。如圖16所示，Ia=Ib，采光場的采光量差不多，但在采光口的光強體方位有差異時，Ia是z坐標采光口的光強體，Ib是z'坐標采光口的光強體，可能有較大的誤差。

在Lγ全云天天穹下，Ia＞Ib，因為Ia采光口z坐標系正對天頂位置，天頂最亮，為4 092.6 cd/m2，Ib采光口z'坐標系正對的是γ－α的天空，此處天穹亮度小于天頂亮度，當α=30°、γ=60°時，天穹亮度為

所以，Ia＞Ib，采光場獲得的采光量要少些，此處光強體的大小和方位也有差異。如改用z｀坐標系積分，采光口光強體的大小和方位都可以解決，但對計算照度（采光系數）的精準度有影響。為此，可轉動天穹來解決問題，如圖17，水平采光口是對準天頂的，現在把γ=60°變成水平采光口的天頂，而代替α=30°的斜屋面采光口，如I40和I50是30°的坡屋面，則用Lα代替Lγ后進行積分。

9 復合型采光口的光強體數學模型

9.1 A型復合采光口光強體數學模型（縱向、橫向天窗）

這種采光口，通常在工業建筑的廠房中使用，窗洞設在屋頂上，沿車間軸向的縱向或橫向布置，是設在屋頂上的豎向矩形類采光口。高度為2.4 m以上，長度不限，與廠房的跨度、高度有關。

圖18復合采光口有兩種，圖18(a)是縱向天窗，沿廠房屋頂軸向設置，常見的是三跨一天窗，若四跨則兩天窗，此時天窗的采光功能會相互影響；圖18(b)是橫向天窗，在同一跨廠房屋頂，沿廠房軸向橫向設置，采光效果必然相互影響。下面分別討論兩種A型復合采光口的采光效果。

9.1.1 A型縱向復合采光口光強體數學模型

三跨一窗是A型縱向復合采光口最簡單的一種布置，是一設置在屋頂上的豎向矩形采光口，其特點是高度有限、長度較大，如圖18(a)所示。在計算這種采光口的采光量時，為滿足點光源的條件，r＞4b、r＞4c，把其分割為多個連續的豎向矩形采光口，或者加大計算（測試）距離（使M在半徑r更大的球面上），即取r＞10 m，設法使面光源接近點光源的條件。

設天窗結構高H=3.0 m，長度不限，把這一長度的豎向矩形窗分成多個c×b=2.4 m×2.4 m的窗段，取其中一個窗段進行研究。天窗內表面對采光的貢獻小，不計其影響，窗的d尺寸小，不計其影響，無窗外遮擋，即無Ld、Lh、Ln的光射入，故只計天穹光Lγ的作用。

將天穹亮度參數sinγ代入“臨界照度”時的天穹亮度分布式（2），再將式（1）代入豎向采光口光強度積分原式（22），并不計d的影響，則有A型縱向復合采光口光強度數學式

縱向天窗有相對的兩排窗面，所以同一個窗段有兩個I60一樣的光強體，采光量加倍。

完成式（37）積分后，再代入α0、β0、γ0各參量：

則可計算和繪制A型縱向復合采光口一個窗段的光強體圖。

9.1.2 A型橫向復合采光口的光強體數學模型

A型橫向復合采光口，如圖18(b)所示。以窗結構高3.0 m，窗高2.4 m，窗結構長25 m，窗長24 m為例。廠房屋頂設計成高低相間的多段結構，在高低兩段的結合處設豎向矩形窗。圖19為該復合采光口的側視圖和水平投影。采光效果見圖19(a)，天然光來自2條通路：天穹光通過采光口注入；天穹光→屋頂（B區）反射→天棚（A區）反射→室內。

1）采光口的第一組天然光

采光口通過采光口采集天穹光能，由于采光口的水平方向較長，只能分成多個窗段計算，b×c=2.4 m×2.4 m為一個窗段，和縱向復合采光口處理方式相同。將sinγ代入“臨界照度”時的天穹亮度分布式（1），再將式（1）代入式（22），若不計采光口相互擋光影響，也不計d的影響，則有A型橫向復合采光口第一組光強體數學模型。

式37（a）與式（36）相同，同是b×c=2.4 m×2.4 m的豎向矩形窗段。橫向窗同樣有兩個窗面，所以在同一個窗段有2個I61光強體，采光量加倍。雙排窗共10個I61光強體。

在式（36）和（37）中，垂直方向0～γ，水平方向α1～α2區域內的光能，從另一側的窗洞射出，削弱了室內采光量。地面和屋頂的反光，進入窗內空間的光可以抵消一些損失。

2）采光口的第二組天然光

此組天然光是A區天棚的反射光，天穹Lγ照明B區房頂，B區屋頂亮度再照射A區天棚，A區天棚的散射光，再進入采光空間，這一組光能不多，但還是對室內采光有貢獻，見圖19(a）。

設定窗尺寸，窗高2.4 m，長24 m，窗結構高3.0 m，屋頂天棚長12 m，寬約24 m。在這些條件下，先求房頂（B區段）亮度L，再求天棚（A區段）亮度Lp，得到天棚（A區段）的散射光光強度I62。屋頂的亮度和天棚的亮度都是不均勻的，可用平均亮度求近似的答案。

將Lγ代入E，求B區屋頂的水平照度為5 170 lx，取屋頂（B區）反射系數ρ=0.25，代入式（4），則屋頂的平均亮度為411.3 cd/m2。查式（22），約定豎窗的透光系數τw=0.5，根據下式：

A天棚的平均照度為58.5 lx，約定A天棚的反射系數ρ=0.5，則A天棚的平均亮度

把A區天棚12 m×24 m，當成亮度為9.3 cd/m2的等亮度發光天棚，或者當成等亮度天穹下的水平采光口，此時d=H，τw=1，Lp=9.3 cd/m2（r=50 m），將矩形水平采光口的積分域代入式（29），則有A區天棚下的光強體數學模型

9.2 B型復合采光口光強體數學模型（等腰三角形鋸齒形天窗）

B型復合采光口，是設在屋頂上的豎向三角形類采光口的變異形。B型三角形類復合采光口的豎向受光面可以同廠房軸向，也可以橫廠房軸向布置。如圖20(a)所示，采光流程見圖20(b)。Lp難尋，數學模型略。

9.3 C型復合采光口光強體數學模型（井式天窗）

這種天窗井口受光，井壁透光（有擋雨板），井底擋光（積水有反光作用），形如柱體、圓形、方形均可，見圖21(a)。其采光效率極差，主要功能是散熱、排煙、排塵。

C型復合采光口的光強體數學模型，是由一屋頂厚度為d的水平天窗光強體減去筒長為H的水平天窗光強體之差。當然其采光口面積相同，見圖21(b)。

9.3.1 方柱形C型復合采光口光強體數學模型

方柱形C型復合采光口（井式天窗）的光強度，可以用兩個采光口厚度不同（d、H）的矩形水平采光口光強度的差來表示。d是屋頂厚度，H是窗井的高度。可用兩個采光口的光強度修正系數差值合成一個光強度修正系數，對此采光口的光強度修正。根據式（11），有

將K和D域代入式（33）I40，則有方柱形C型復合采光口的光強體數學模型

9.3.2 圓柱形C型復合采光口光強體數學模型

將K和積分域D代入式（34）I50，則有圓柱形C型復合采光口的光強體數學模型：

以上討論了3大類型、9個采光口的光強體數學模型。其他造型的采光口，可將相關參數代入相應的光強體積分原式，即可獲得該 造型采光口的光強體數學模型。同一個采光口，因窗外光源的變化，會有形狀、大小不同的光強體，若窗口尺寸改變時，又會有形狀相同、大小不同的光強體。

上述研究只考慮天穹光和地穹光作用時的采光口配光，若加入插隊光源Ln、Lh的作用，同一個采光口，會衍生出更多的光強體，數學模型將變得十分復雜。

若在采光口光強體數學式中，采用等亮度Lc=3 183.1 cd/m2，則數學式將簡化許多。

10 應用（采光計算）

采光口的配光和燈具配光類似，兩者僅僅是光源有別。采光口的光源是全云天天穹散射光和衍生的地穹光，以及此兩者間的插隊光源Ln、Lh，而燈具是人工光源。采光口和燈具，同樣有一個光強體，因此，人工照明和天然采光是可以用同一方法進行計算的。

10.1 光場

以一個工廠車間為例，根據需要設有多個天窗和側窗，房間的采光效果與采光口和室內環境有關，房間內表面的反光系數大，則反射光對工作面的照度貢獻大，室內工作面的照度均勻度高，立面照度亦高，則采光效果佳，反之則差。采光空間，如圖22所示，以ABCDA工作面為界，分成采光區、地板區。任何一個采光口內側光能分成兩部分：一部分在O-ABCDA錐角內，用f2表示，直接投到工作面上，并在工作面的網點1、2……n處，創造了參差不齊的直射光照度E1；另一部分f1，投到采光區的垟面和天棚上，進入空間漫反射光流程，此時一部分光能滲入工作面，提高了工作面的照度。直射光f2，除在工作面網點上創建直射光照度E1外，在地板區經漫反射流程，滲出的光能進入采光區，進行與f1相同的漫反射光流程，一部分滲出的光能落在工作面上，與f1的滲出光共同創造了工作面散射光平均照度E2。

無論是采光區，還是地板區，都存在區域空腔內的漫反射過程，簡稱光流程，才能形成投到工作面上的照度光。兩個區域的入射光和輸出光有一相對比例，這一比例用區域光效率η1、η2表示。η的大小與采光空間內表面的反射系數緊密相關。

10.2 采光口內光能分割

采光口內側光能都表現在采光口的光強體中，光強體由該采光口的光強體數學式表示。光強體積分原式（22）和式（29）IM，是采光口在OM方向與O-x、y、z坐標軸正向之間夾角α0、β0、γ0標定的光強度。在各個采光口的實例中，光強體數學式和光強體中光強度I的方位，由I矢量與坐標系O-x、y、z坐標軸正向之的夾角標定。

為計算采光口光強體包裝的光能量，把I的方位改為兩個參數表示。豎向采光口光強度I，如圖23(a)所示，用α0和βx角約定，βx從y軸正向逆時針0～2π繞x軸旋轉。水平采光口的光強度I如圖23(b)所示，用γ0和αz角約定，αz從x軸正向逆時針0～2π繞`z軸旋轉。

采光口光強體圈定的光能量f，可以通過球帶系數法積分求解，則有豎向采光口

如圖22所示，整個采光空間以ABCDA工作面分成上下兩個部分，上部稱采光區，下部稱地板區。房間轉角數≥3。一個采光空間，根據需要可設置多個水平采光口Ⅰ和多個豎向采光口Ⅱ，或稱天窗和側窗。這些采光口的坐標原點O，都可以與工作面的轉角點作一連線，對每個采光口而言，這些連線圍成了一個立體角

在圖22中，采光空間設有兩類采光口Ⅰ、Ⅱ。每個采光口的光能分成兩個部分：一部分f2直達工作面ABCDA，其他部分f1，落在采光區的垟面和天棚上，再經過垟和天棚的散射，才有一部分到達工作面。

圖24是圖22中水平采光口Ⅰ的f2積分域，是O-ABCDA錐角在以r為半徑，在－z方向半球面上截割的球缺。該區域為γ01→π。這球缺對應采光口Ⅰ的光強體有相應的區域。因此，對此區域，用球帶系數法積分，即可獲得Ⅰ采光口投向工作面ABCDA的直射光

則有Ⅰ采光口投到采光區的垟面和天棚面的光能

把采光空間所有采光口的光能f全部收集起來，則有采光口向采光空間提供的光能總量

采光口向工作面提供直接光的光能總量F2，也是采光口投向地板區域的光能總量

采光口投向采光區的垟面和天棚的光能總量

10.3 區域光效率

采光空間所受光能為F（lm），不可能全部落到工作面上。光能F分成兩部分，一部分F1留在采光區進行第一次漫反射，一部分光落在工作面，到達地板區的光又在地板區進行一次漫反射，有少量光能返回采光區，完成一次光流程，F1返回采光區的光再重復前一光流程。若F1經過兩區間多次漫射光流程，從采光區到工作面（地板區）的光能總流量為F1'，則采光空間對F1有光效率η1存在。散射光流程見圖25。

另一部分光能F2直接投到工作面和地板區，F2首先在地板區進行F1一樣的光流程，滲出一部分光進入采光區，這一部分光重復F1的光流程，產生落到工作面的有用光。若F2經過多次光流程，產生落到工作面的光能總量為F2｀，則采光空間對F2有光效率η2存在。

在采光空間存在下列光環境時：采光區——門、窗、垟面、天棚的平均反光系數為ρ1，面積為S1；地板區——門、垟面、地板的平均反光系數為ρ2，面積為S2；工作面（ABCDA）面積為S，透光系數為τ=1，則正向（采光區→地板區）工作面平均透光系數

負向（地板區→采光區）工作面平均透光系數

F1、F2在工作面兩邊的區域（采光區、地板區）來回游動時受區域平均反射系數的驅使，完成n次散射光流程。由此可計算出正向穿越工作面的光通量，則采光空間促成F1、F2的工作面照度光能的光效率η1、η2可求。

1）流程：F1→采光區→工作面（地板區）。

第一輪回：F1在采光區進行n次漫射光流程，溢出正向光能（采光區→地板區）。

則在采光空間中的F1，在采光區的第一輪回中溢出的正向光能為或F1η（1），所以有

2）F1n次輪回光流程溢出的正向光能總量。

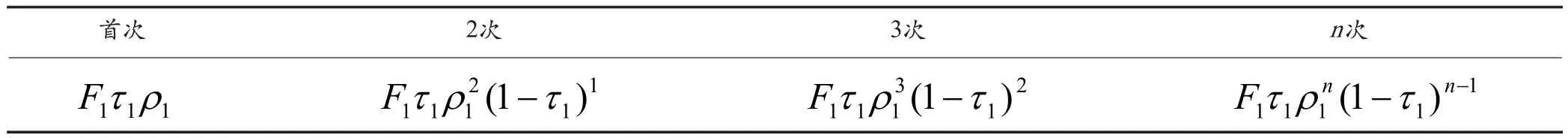
首次2次 3次n次F1τρ12F ρ τ)Fτ ??ρ1 1 1 2 1 1 1( τ)Fτ ?1 3 1 1 1 ρ(1 τ)11 1 τn 1(1? n1 1

所以采光區F1溢出的光能總量約為

則采光空間對F1的光效率近似值

3）F2→地板區→采光區，在第一輪回漫反射光流程中，溢出的負向光能（n次）。

4）F2在地板區漫射，溢出的光投入采光區，重復F1的光流程。F2經過n次輪回溢出的正向光能總量約為F2η(2)η1。

第1回 第2回 第3回 第n回F1η η（ η F n1 F?1 2 2 1 1 ）（）（1） η（η1 ）（）η（ η2 2 3 1 Fn 11）（2）

故采光空間促成F2的光效率近似值為

10.4 工作面照度

10.4.1 直射光照度

在工作面的坐標網點上，1～n，見圖22(b)，所有的點位，如第m點，所有的采光口Ⅰ、Ⅱ的坐標原點O，都可以與點位m作一連線，則采光口在連線方向，對網點m有一光強度I存在。故此采光口對網點m有直射光照度

所有的采光口對網點1～n，有直射光照度

10.4.2 散射光能和工作面照度

采光口投入采光空間的總光能量F見式（42），F投到工件面的是直接光。投到采光區垟面和天棚的光能F1。F1和F2，經過采光空間反復光煉后，光效率η1、η2見式（43）和（44），提供給工作面的光能為

因此，有工作面的散射光平均照度

式中，S為工作面面積，m2。

則有工作面的平均照度Ev，代表整個工作面的照度水平：

在工作面網點上的直射光照度，存在最大值和最小值emax、emin，則工作面上有最大照度和最小照度：

用區域光效法計算工作面的平均照度

Ev簡化式

式（47）中：Ev為工作面平均照度，lx；S為工作面面積，m2；F為采光空間的采光量，lm；F1為采光區的墻面、門、窗、天棚第一次接收到的采光量，lm ；F2為工作面接收的直接光，lm；ρ1τ1為采光區的門、窗、墻和天棚的平均反光系數ρ1，工作面正向平均透光系數τ1；ρ2τ2為地板區門、墻、地板的平均反光系數ρ2，工作面負向平均透光系數τ2。

10.5 采光系數和均勻度

工作面的照度與室外無遮擋水平照度的百分比，稱為采光系數。

在“臨界照度”為10 000 lx的環境下，采光系數可表示為

用工作面的最低照度比工作面的最高照度，表示工作面的采光均勻度（又是照度均勻度）。

均勻度V，表示在工作面上的照度或采光系數達到的質量。V在0～1的區間，V值接近1為最佳。

采光口的配光和燈具的配光相似，每個燈具都有自身的光強體。人工照明的照度計算，也可以用上述采光計算方法計算，只要把燈具的配光曲線（光強體）轉化為數學模型表示即可。如此方法，不用查表，就可以完成人工照明的計算，采光、照明計算合二為一。

11 探索

11.1 其他亮度天空的采光口光強體數學模型

選用蒙·斯本塞提出的全云天天空亮度分布的天空作為采光口的天然光源，且在“臨界照度”為104lx時，研究各種典型采光口的光強體數學式。

天空亮度是不穩定的，因時間、季節和云量的變化而不同，國際照明學會（CIE）認可的有代表性的天空亮度為15種。

無論何種天空亮度分布，在E0=104lx時，只要這種天空亮度分布是連續函數，將相對應的地穹亮度分布代入原式（22）和（29），就有該采光口在此天空下的光強體數學模型。

若用E0=104lx的等亮度天穹為亮度源，數學模型會簡化許多。

采光口光強體數學模型的數學式比較繁瑣，但可以用現代計算機技術解決。如果繞過數學式求光強體，也是有可能的。例如，為了獲得某一形狀采光口，在某種天穹亮度分布和相應的地穹亮度分布下的光強體，則模擬這種天穹在“臨界照度”時的天穹亮度分布和相應的地穹亮度分布。將采光口置于該環境里，測試采光口內側各個OM方向的“光強度值”，則獲得此采光口在該天穹下的光強體圖。這無疑是一條捷徑。

11.2 采光口光強體的意義

有了采光口內半球面的光強度分布，則可求采光場內工作面各網點的直射光照度Ei。Ei加散射光的平均照度則工作面各網點照度Ei有Emax、Emin，可以用計算機繪制工作面的照度（采光系數）波幅圖，這是當前所有的采光設計都無法實現的。

采光計算和人工照明可用同一種計算方法，因為采光口和燈具都有類似的光強度、光強體。

11.3 采光口的厚度d（圍護結構）

在采光口內半球面上，測點M的位置不同，所見到的采光口面積各異，是因采光口圍護結構厚度d遮擋的影響，所以每個采光口每個M點都有一個修正系數K。K代表M點見到的有效窗面（天空），K是一個變量（因M位置不同而不同）。

12 結論

數學是人類文明的基石之一，用數學模型塑造采光口的光強體（光強度），是新的采光計算方法。以立體角投影定律為依托，探索了從亮度源L光能經采光口至受光點照度E（C）的既簡單（光流程）又復雜（光強體數學式）的過程。