線性代數教學中幾個問題的解析及延伸

田凱　張孟霞

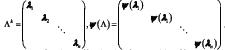
摘 要 在線性代數課程中，矩陣的相關計算占據大量篇幅。從幾個計算方陣的冪函數、多項式的題目出發，在詳細分析解題思路的基礎上，引申出更一般的矩陣知識。

關鍵詞 方陣的冪 方陣的多項式 方陣的可對角化 Jordan形矩陣

中圖分類號：G642文獻標識碼：A

做為一個數學分支，線性代數主要研究行列式、矩陣、線性方程組、向量、有限維向量空間和線性變換，在自然科學、工程技術的眾多領域有廣泛應用. 在我國本科專業的課程體系中，線性代數是理、工、經、管類專業本科生的基礎必修課. 該課程旨在介紹行列式、矩陣、線性方程組、相似矩陣、二次型、向量空間等線性代數的基本概念、理論和方法. 在線性代數課程的教學中，線性方程組、矩陣、向量組，三者的聯系發揮著至關重要的作用，也是學好這門課程的關鍵。

矩陣的相關計算問題，例如：初等變換法計算矩陣的秩、初等變換法求逆矩陣、對稱矩陣的對角化等，在線性代數的教學中占據很大比例。在線性代數課程的教學實踐中，筆者發現結合具體問題將知識進行適當地延伸，有助于學生理解問題的本質、掌握方法的核心，顯著提高學生運用知識解決復雜問題的能力。本文將以幾個計算方陣的冪、方陣的多項式的題目為例，分析解題方法，介紹與它們相關的延伸知識.

問題一：已知3維列向量，，且，求。

同類問題參見文獻[1]習題二第7題（2）。

解析：為找到合理的計算方法，不妨先嘗試計算，和。 我們有

因為矩陣乘法滿足結合律，所以可以將以上三式分別改寫為

此時注意到，是一個數，即。 于是

根據數學歸納法，不難發現，對于正整數，我們有

上式中令，即可得到問題一的結果。

延伸：問題一并非個例。若階方陣的秩為1，則必定存在維非零列向量和，使，于是我們可用上述方法，計算方陣的冪函數. 事實上，文獻[1]習題三第20題，告訴我們

命題1：行列的矩陣的秩為1的充分必要條件是存在維非零列向量和維非零列向量，使。

命題1又是如下命題的特例。

命題2：行列的矩陣的秩為，則存在行列的列滿秩矩陣和行列的行滿秩矩陣，使。

在矩陣理論中，這個命題被稱為矩陣的滿秩分解. 在矩陣論的相關教材中，不難找到命題2的證明，這里不再贅述. 應該強調，矩陣的滿秩分解并不唯一。 矩陣的滿秩分解是一種基本、但重要的矩陣分解方法，在機器識別、模式識別、人工智能等領域有廣泛應用。

問題二：已知3階方陣，求，。

同類題目參見文獻[1]習題五第17題、第25題.

解析：直接計算可得，3階方陣有三個互不相等的特征值，和，所以可斷定，方陣可對角化，即存在3階可逆矩陣，使為對角矩陣。通過計算，我們發現方陣的屬于特征值，和的線性無關的特征向量分別是

令，則有，或等價地寫為。

于是，對任意正整數，。對于次多項式

有。 一般地，對角矩陣的冪、多項式由下式給出

因此，方陣的冪函數、多項式都可以具體算出。

方陣的對角化，尤其是實對稱矩陣的對角化，是線性代數課程的重點內容。我們知道，階方陣可對角化的充分必要條件是有個線性無關的特征向量。

對于階實對稱矩陣，存在正交矩陣使為對角矩陣。實對稱矩陣可通過正交相似變換化為對角矩陣，還被用于化簡二次型，即通過正交線性變換將二次型化為標準形。

延伸：除實對稱矩陣外，一些特殊矩陣，如實反稱矩陣、正交矩陣、埃爾米特矩陣、酉矩陣等，都是可對角化的。接下來，我們簡要解釋這些事實。

考慮行列的復矩陣，的共軛矩陣為，其中是的復共軛;的共軛轉置矩陣為。

定義：若級復矩陣滿足，則稱是一個埃爾米特矩陣。

定義：若級復矩陣滿足，則稱為一個酉矩陣。

容易發現，若為酉矩陣，則可逆且。

定義：若級復矩陣滿足，則稱是一個正規矩陣。

實對稱矩陣、實反稱矩陣、正交矩陣、埃爾米特矩陣、酉矩陣都是正規矩陣。

引理：對任意級復矩陣，存在級酉矩陣使為上三角矩陣，即

其中。是的特征值。

這個引理被稱為Schur引理，是矩陣分解理論中的一個基本引理。對矩陣的階數做歸納，即可證明此引理。這里不再贅述其證明過程。

引理：上（下）三角形正規矩陣是對角矩（下轉第218頁）（上接第188頁）陣。

基于上述兩個引理，可以證明：

命題：若級復矩陣是正規矩陣，則存在級酉矩陣使

其中是的特征值。

問題三：已知4階方陣，求。

同類問題參見文獻[1]習題二第6題（2）。

解析：易知方陣有一個特征值，且屬于此特征值的線性無關的特征向量是，故方陣不可對角化. 我們不能用問題二的解法處理這個問題。

注意到，其中。因為單位矩陣與同階方陣總是可交換的，所以對于正整數，可以用二項展開式將寫為

又因為方陣有如下性質，即

所以，當時，

延伸：方陣是4階Jordan塊矩陣。事實上，

定義：形如

的階方陣稱為一個階Jordan塊矩陣. 由Jordan塊矩陣組成的分塊對角矩陣，如

稱為Jordan形矩陣。

階Jordan塊矩陣的多項式的一般公式是：設多項式，則

矩陣理論中的一個重要結果是：任意階方陣都與一個Jordan形矩陣相似. 若不考慮Jordan形矩陣中Jordan塊的排列順序，則Jordan形矩陣是被方陣唯一決定的，稱為方陣的Jordan標準形。

Jordan標準形在矩陣理論中起著十分重要的作用。例如：以Jordan標準形為基礎，可以給出方陣的指數函數、正（余）弦函數等矩陣函數的計算公式。感興趣的讀者，可以查閱矩陣分析方面的文獻。

*通訊作者：田凱

基金項目：中國礦業大學（北京）教學團隊建設項目“《線性代數》教學內容改革和資源建設”，項目編號：J180714。

作者簡介：田凱（1982-），男，河北省石家莊市，理學博士，中國礦業大學（北京）理學院，副教授（通訊作者），研究方向為可積系統及其應用;張孟霞（1978-），女，山西省聞喜縣，理學博士，中國礦業大學（北京）理學院，副教授，研究方向為可積系統及其應用。

參考文獻

[1] 同濟大學數學系.工程數學線性代數（第六版）[M].北京：高等教育出版社，2014.

[2] 蘇育才，姜翠波，張躍輝.矩陣理論[M].北京：科學出版社，2006.

[3] 姜志俠，孟品超，李延忠.矩陣分析[M].北京：清華大學出版社，2015.

[4] 王萼芳，石生明.高等代數（第五版）[M].北京：高等教育出版社，2019.