基于果蠅算法的氣田集輸布局優(yōu)化
王昊 魏立新 陳雙慶


摘? ? ? 要: 為降低地面集輸系統(tǒng)氣田成本和提高生產(chǎn)效率,在站場(chǎng)選址、站間管線連接方式等一系列環(huán)節(jié)進(jìn)行人工智能布局優(yōu)化,以達(dá)到線路最短或工程建設(shè)總投資最小的目的。本文將采用一種較新的智能算法果蠅算法對(duì)氣田集輸系統(tǒng)進(jìn)行布局優(yōu)化。根據(jù)果蠅個(gè)體通過(guò)嗅覺(jué)尋找食物的原理,以項(xiàng)目總投資最小為目標(biāo)函數(shù),根據(jù)地面集輸系統(tǒng)的要求,找到約束條件,建立優(yōu)化數(shù)學(xué)模型,通過(guò)MATLAB軟件實(shí)現(xiàn)算法的運(yùn)算,并對(duì)優(yōu)化結(jié)果進(jìn)行仿真,找出地面布局下氣田管網(wǎng)的最優(yōu)連接方式。經(jīng)過(guò)果蠅算法的優(yōu)化,氣田地面集輸管網(wǎng)可以顯著降低工程投資成本。通過(guò)與傳統(tǒng)的遞階優(yōu)化方法的比較,說(shuō)明了該算法在收斂速度和優(yōu)化精度方面的優(yōu)勢(shì)。
關(guān)? 鍵? 詞:集輸系統(tǒng);布局優(yōu)化;果蠅算法;對(duì)比分析
中圖分類號(hào):TE862;TE89? ? ? ? 文獻(xiàn)標(biāo)識(shí)碼: A? ? ? 文章編號(hào): 1671-0460(2020)11-2507-05
Optimization of Gas Field Gathering and Transportation
Layout Based on Drosophila Algorithm
WANG Hao, WEI Li-xin, CHEN Shuang-qing
(School of Petroleum Engineering, Northeast Petroleum University, Heilongjiang Daqing 163318, China)
Abstract: In order to reduce the cost of the gas field in the ground gathering system, and improve production efficiency, the artificial intelligence layout optimization is always carried out to achieve the shortest route or the minimum investment of the project constructionin the selection of the station site, the connection between the station and the pipeline. In this paper, the layout of gas field gathering and transportation system was optimizedby a relatively novel intelligent algorithm, drosophila algorithm. Using the principle of fruit flies searching for food through olfactory, taking the minimum total investment of the project as the objective function, the constraints were found according to the requirements of the ground gathering system, and the optimized mathematical model was established. The algorithm was run by MATLAB software and the optimization results were simulated to find the optimal gas field pipe network connection in the layout. After the optimization of the drosophila algorithm, the engineering investment costof the gas field ground gathering pipeline network was significantly reduced. Through comparison and analysis with traditional grading optimization method, the drosophila algorithm showed the advantages in terms of convergence speed and optimization accuracy.
Key words: Gathering and transportation system; Layout optimization; Drosophila algorithm; Comparative analysis
目前,氣田集輸管網(wǎng)布局優(yōu)化通常采用層次優(yōu)化法[1-2],將集輸系統(tǒng)的整體切割劃分為若干部分,并依次進(jìn)行優(yōu)化。首先優(yōu)化井組分布[3-6],其次選擇管線長(zhǎng)度最短的集氣站和集氣末站位置作為目標(biāo)函數(shù)。層次優(yōu)化的缺點(diǎn)是每一級(jí)優(yōu)化都可能是局部最優(yōu)解,但不能保證是全局最優(yōu)解[7]。
本文使用的果蠅算法[8]是臺(tái)灣學(xué)者潘文超在2011年提出的,它是一種啟發(fā)式全局優(yōu)化的進(jìn)化智能算法。以果蠅的覓食行為為基礎(chǔ),推導(dǎo)出全局最優(yōu)解,具有調(diào)節(jié)參數(shù)少、操作簡(jiǎn)單、性能好等優(yōu)點(diǎn)。
本文以徑向管網(wǎng)與分支管網(wǎng)相結(jié)合的氣田集輸系統(tǒng)布置為例[9-14]。氣田集輸工藝是從氣井中收集天然氣,經(jīng)集氣管線輸送,在集氣站中脫硫脫碳后加工成成品氣并儲(chǔ)存的工藝[15-21]。
1? 數(shù)學(xué)模型
1.1? 目標(biāo)函數(shù)
在氣田集輸管網(wǎng)的拓?fù)洳季謨?yōu)化中,已有研究成果多以管網(wǎng)總長(zhǎng)度最小或者管網(wǎng)總建設(shè)費(fèi)用最小為目標(biāo)函數(shù)。本文實(shí)例將以管網(wǎng)的總投資費(fèi)用最小為目標(biāo)函數(shù),包括采氣管道建設(shè)費(fèi)用、集氣管道建設(shè)費(fèi)用、集氣站建設(shè)費(fèi)用3個(gè)部分。
F=F_1+F_2+F_3? ? ? ? ? ? ? ? (1)
F_1=∑_i^N?∑_j^M??_(i,j)? β_(?,i,j) C_(?,i,j)? ? ? ? ? ? (2)
F_2=∑_i^(M+G)?∑_j^(M+G)?θ_(i,j)? β_(θ,i,j) C_(θ.i.j)? ? ? ? ? (3)
F_3=∑_i^M?f(S_i )? ? ? ? ? ? ? ? (4)
式中:F—管網(wǎng)建設(shè)總投資費(fèi)用;
F_1—采氣管道建設(shè)費(fèi)用;
F_2—集氣管道建設(shè)費(fèi)用;
F_3—集氣站管道建設(shè)費(fèi)用;
??〖? ? ? ? ? ? ?〗_(i,j)—“井站”管網(wǎng)第i節(jié)點(diǎn)和第j節(jié)點(diǎn)之間連接二元變量,?_(i,j)=1時(shí)
表示第i節(jié)點(diǎn)和第j節(jié)點(diǎn)處于連接狀態(tài),?_(i,j)=0時(shí)表示第i節(jié)
點(diǎn)和第j節(jié)點(diǎn)處于未連接狀態(tài);
β_(?,i,j)—采氣管道長(zhǎng)度;
C_(?,i,j)—單位采氣管道的建設(shè)費(fèi)用,與管材、管徑有關(guān),可由最小
二乘法求得;
θ_(i,j)—“站站”管網(wǎng)第i節(jié)點(diǎn)和第j節(jié)點(diǎn)之間連接二元變量,?_(i,j)=1時(shí)
表示第i節(jié)點(diǎn)和第j節(jié)點(diǎn)處于連接狀態(tài),?_(i,j)=0時(shí)表示第i節(jié)
點(diǎn)和第j節(jié)點(diǎn)處于未連接狀態(tài);
β_(θ,i,j)—集氣管道長(zhǎng)度;
C_(θ,i,j)—單位集氣管道的建設(shè)費(fèi)用,與管材,管徑有關(guān),可由最小
二乘法求得;
S_i—第i個(gè)集氣站處理量;
i∈N,j∈M,N—生產(chǎn)井個(gè)數(shù),M—集氣站個(gè)數(shù);
G—外輸站個(gè)數(shù)。
1.2? 約束條件
1.2.1 “井站”隸屬關(guān)系唯一性約束
一口井只可以隸屬于一個(gè)站
?_(i,j)=1? ? ? ? ? ? ? (5)
1.2.2? 站處理能力的約束
站的建設(shè)需要消耗大量成本,在保證安全生產(chǎn)運(yùn)輸?shù)那疤嵯拢瑧?yīng)該盡可能提高站的利用率。同時(shí),受到管材、管徑以及流速的限制,為了保證安全,站的處理量要有上限值。
∑_i^N??_(i,j)? s_i=S_j? ? ? ? ? ? (6)
S_MIN "≤" S_j "≤" S_MAX? ? ? ? ? ?(7)
式中:s_i—第i口井的產(chǎn)氣量;
S_MIN—站最小處理量;
S_MAX—站最大處理量。
1.2.3? 集輸半徑約束
井與站或是站與站之間的管線距離不應(yīng)該大于允許的集輸半徑。
?_(i,j) β_(?,i,j)≤R(i=1,2,…,N;j=1,2,…,M)? (8)
式中:R—集輸半徑。
1.2.4? 取值范圍約束
目標(biāo)函數(shù)中的決策變量應(yīng)在其取值范圍內(nèi)進(jìn)行優(yōu)化求解。
?_(i,j)={█(&1節(jié)點(diǎn)i與節(jié)點(diǎn)j相連@&0其他)┤? ? ? ? (9)
θ_(i,j)={█(&1節(jié)點(diǎn)i與節(jié)點(diǎn)j相連@&0其他)┤? ? ? ?(10)
2? 算法求解
2.1? 果蠅算法
果蠅算法(Fruit Fly Optimization Algorithm, FOA)屬于群體演化式人工智能的一種新方法,由臺(tái)灣學(xué)者潘文超于2011年提出。果蠅算法的原理是依據(jù)果蠅個(gè)體應(yīng)用其良好的嗅覺(jué)器官捕捉分析空氣中的各種氣味,從而達(dá)到食物源的目的。在氣田集輸系統(tǒng)的布局優(yōu)化中,對(duì)于氣井個(gè)體進(jìn)行類似于果蠅個(gè)體的編碼從而轉(zhuǎn)化為數(shù)學(xué)模型,利用果蠅群體捕獲食物源氣味的原理,進(jìn)行氣田區(qū)塊氣井的布局優(yōu)化。果蠅算法相比于傳統(tǒng)分級(jí)優(yōu)化方法,它的優(yōu)勢(shì)在于可以避免因分級(jí)優(yōu)化而出現(xiàn)局部最優(yōu)解的現(xiàn)象;果蠅算法相比于其他的一些人工智能算法,它的優(yōu)勢(shì)在于主控參數(shù)的靈活性和易操作性,以及基因編碼的簡(jiǎn)易性和較快的收斂速度。
2.2? 主控參數(shù)
2.2.1? 果蠅編碼
對(duì)于給出的氣田中氣井的個(gè)數(shù)進(jìn)行分組排序,根據(jù)分布經(jīng)驗(yàn)一般一個(gè)集氣站將會(huì)管轄6~7口氣井,第一個(gè)果蠅個(gè)體的編碼為:
C_1={w_1,w_2,…w_6;w_7,w_8,…w_13;……;w_49,w_50,…w_55 }
式中:w_i對(duì)應(yīng)氣井的位置編號(hào);
w_1-w_(i-1)對(duì)應(yīng)6~7口氣井作為一個(gè)集氣站所管轄的數(shù)量。
由此可以得出對(duì)比方案中的其他果蠅個(gè)體的編碼。
C_2={w_1,w_2,…w_7;w_8,w_8,…w_14;……;w_50,w_51,…w_55 }
C_3={w_1,w_2,…w_6;w_7,w_8,…w_14;……;w_50,w_51,…w_55 }
2.2.2? 味覺(jué)濃度判定值(T_i)
最初由于無(wú)法得知食物具體位置,因此需要先估計(jì)與原點(diǎn)的距離D_i,再計(jì)算味覺(jué)濃度判定值T_i,此值為距離的倒數(shù)。
Di =(xi2+yi2)0.5? ? ? ? ? ?(11)
T_i=1?D_i? ? ? ? ? ? ? ?(12)
2.2.3? 味覺(jué)濃度(Smell_i)和味覺(jué)濃度判定函數(shù)
味覺(jué)濃度是判定一個(gè)果蠅個(gè)體(優(yōu)化方案)的優(yōu)劣,它需要將味覺(jué)濃度判定值T_i代入味覺(jué)濃度判定函數(shù)。本文應(yīng)用的判定函數(shù)是通過(guò)分析氣井布局優(yōu)化而得出。
(13)
2.2.4? 終止精度
終止精度也可以稱為最大迭代次數(shù),當(dāng)算法迭代次數(shù)達(dá)到優(yōu)化結(jié)果所允許的精度誤差范圍之內(nèi),或者迭代次數(shù)得到的優(yōu)化結(jié)果趨于穩(wěn)定不在大幅度波動(dòng)時(shí),停止迭代。
2.3? 算法流程
1)隨機(jī)初始果蠅群體的位置X_— "axis" 和Y_— "axis" ;設(shè)定最大迭代數(shù)Maxgen;給定果蠅群體的規(guī)模sizepop。本實(shí)例中,算法的種群規(guī)模為20,迭代次數(shù)為200次。
2)賦予果蠅個(gè)體利用嗅覺(jué)搜尋食物的隨機(jī)方向與距離,生成初始種群:
{█(&X_i=X_axis+RandomValue@&Y_i=Y_axis+RandomValue)┤? ? ?(14)
式中,RandomValue為搜索方向和距離。
本實(shí)例中,搜索方向和距離如公式15所示:
{█(&X_i=X_axis+2·rand-1@&Y_i=Y_axis+2·rand-1)┤? ? ? ? (15)
3)最初由于無(wú)法得知食物具體位置,因此需要先估計(jì)與原點(diǎn)的距離D_i,再計(jì)算味道濃度判定值T_i,此值為距離的倒數(shù)。將味道濃度判定值T_i代入味道濃度判定函數(shù)(Fitness function),求出該果蠅個(gè)體位置的味道濃度(Smell_i)。
4)尋找出果蠅種群中味道濃度最小的一個(gè)(求最小值)。
[bestSmell,bestindex]=min?(Smell_i ) (16)
5)保留最佳味道濃度值的x,y坐標(biāo),此時(shí)果蠅群體利用視覺(jué)往該位置飛去。
{█(&X_axis=X(bestindex)@&Y_axis=Y(bestindex)@&Smellbest=bestSmell)┤? ? ? ? (17)
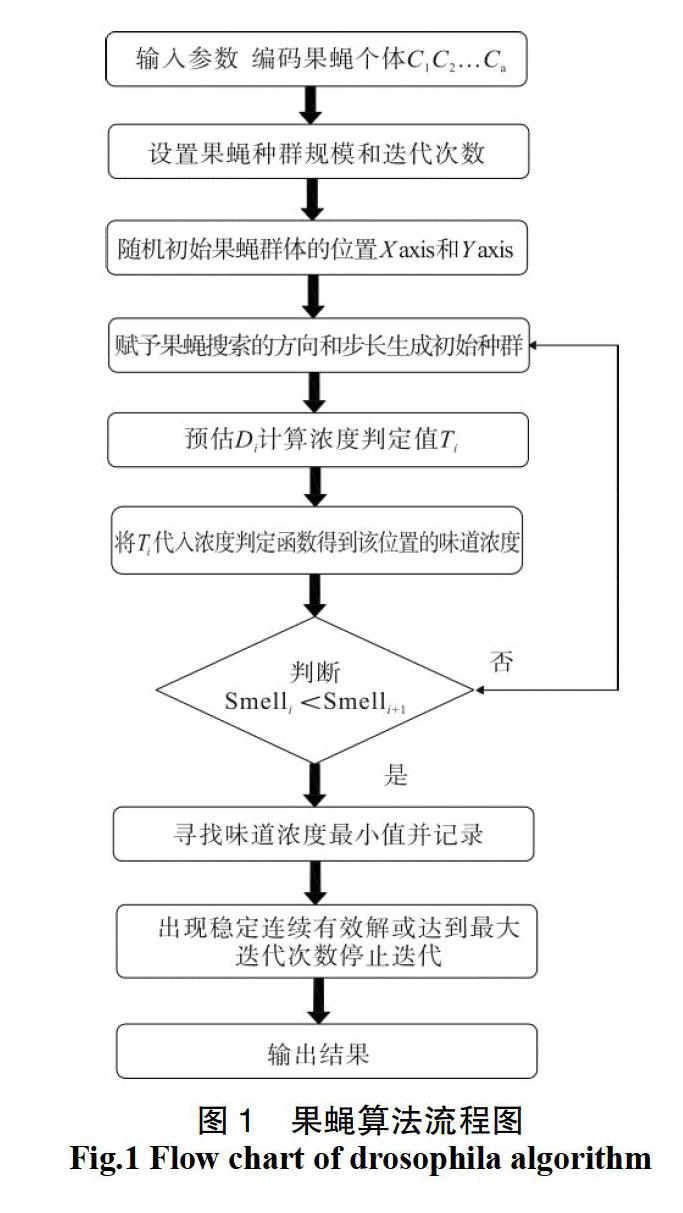
6)進(jìn)入迭代尋優(yōu),重復(fù)執(zhí)行步驟(14),并判斷味道濃度是否優(yōu)于前一代的味道濃度。若是則執(zhí)行步驟5,當(dāng)出現(xiàn)連續(xù)穩(wěn)定的有效解或者達(dá)到最大迭代次數(shù),算法停止,流程圖如圖1。
3? 實(shí)例計(jì)算
某氣田有氣井24口,井組優(yōu)化后需集氣站4座,中心外輸站1座,組成一個(gè)放射狀和枝狀組合的集輸管網(wǎng)系統(tǒng)。首先應(yīng)用傳統(tǒng)的分級(jí)優(yōu)化方法對(duì)管網(wǎng)進(jìn)行優(yōu)化設(shè)計(jì),算法設(shè)計(jì)參數(shù)優(yōu)化結(jié)果如圖4所示,優(yōu)化數(shù)據(jù)如表1所示。應(yīng)用本文介紹的果蠅算法進(jìn)行管網(wǎng)的優(yōu)化設(shè)計(jì),優(yōu)化結(jié)果如圖5所示,優(yōu)化數(shù)據(jù)如表2所示。兩種優(yōu)化方法的對(duì)比結(jié)果如表3所示。
本實(shí)例中,算法的種群規(guī)模為20,迭代次數(shù)為200次。計(jì)算過(guò)程的數(shù)據(jù)變化如圖2、圖3所示。
由圖3可知,在集氣總站位置坐標(biāo)為(245,415)的時(shí)候,集輸系統(tǒng)建設(shè)總投資費(fèi)用(味覺(jué)濃度)達(dá)到最小值,122689.35萬(wàn)元。
從表1、表2、表3的數(shù)據(jù)可以看出,采用傳統(tǒng)的分層優(yōu)化方法進(jìn)行優(yōu)化時(shí),雖然可以得到每一步的最優(yōu)解,但當(dāng)管網(wǎng)整體組合時(shí),局部管的長(zhǎng)度會(huì)增加,從而增加管網(wǎng);當(dāng)采用果蠅算法進(jìn)行優(yōu)化時(shí),將氣井、集氣站、集氣末站作為一個(gè)整體進(jìn)行處理,其目標(biāo)是使管網(wǎng)的投資成本最小化,避免整個(gè)模型因最小管道長(zhǎng)度而陷入局部最優(yōu)解的誤區(qū)。結(jié)果表明,果蠅算法計(jì)算的管網(wǎng)建設(shè)成本比傳統(tǒng)的分層優(yōu)化方法低12.2%,優(yōu)化效果顯著。
4? 結(jié) 論
1)以管網(wǎng)總投資最小為目標(biāo)函數(shù),建立了優(yōu)化模型,采用果蠅算法對(duì)數(shù)學(xué)模型進(jìn)行求解,最終求出在管網(wǎng)總建設(shè)投資最小情況下的集氣站、集氣總站的站址選擇以及各管段的長(zhǎng)度。
2)采用果蠅算法這種新型啟發(fā)式智能算法,根據(jù)氣田情況,適當(dāng)調(diào)整果蠅群體大小和迭代次數(shù),以便于快速準(zhǔn)確地計(jì)算數(shù)學(xué)模型,得到良好的優(yōu)化結(jié)果。
3)用兩種方法對(duì)氣田集輸管網(wǎng)進(jìn)行優(yōu)化設(shè)計(jì)比較,結(jié)果表明,本文采用的果蠅算法相對(duì)于傳統(tǒng)分級(jí)優(yōu)化方法來(lái)說(shuō),優(yōu)化過(guò)程時(shí)間更短,優(yōu)化效果更顯著,更節(jié)約氣田集輸管網(wǎng)的建設(shè)投資費(fèi)用。
參考文獻(xiàn):
[1]劉光金.油氣田地面集輸管網(wǎng)的優(yōu)化設(shè)計(jì)[J].油氣田地面工程,2014,33(5):7-8.
[2]潘紅麗,楊鴻雁. 氣田地面集輸管網(wǎng)系統(tǒng)的優(yōu)化設(shè)計(jì)[J]. 油氣儲(chǔ)運(yùn),2002,21(4):14-18.
[3]李波,余紅偉.管網(wǎng)布局規(guī)劃技術(shù)綜述[J].石油規(guī)劃設(shè)計(jì),2001,12(1):16-18.
[4]黎彬,張烈輝,唐海燕,等.基于微粒群算法的井組劃分方法[J].油氣田地面工程,2008,27(2):36-37.
[5]柳潔,孫潔,鄧志安,等.幾種集輸管網(wǎng)井組劃分方法的比較[J].石油工程技術(shù)監(jiān)督,2011,27(1):1-3.
[6]甄寶軍,梁政,鄧雄.一種天然氣集輸管網(wǎng)井組劃分的新方法[J].管道技術(shù)與設(shè)備,2005(3):7-8.
[7]李自力,孫云峰,張子波,等. 基于遺傳算法的氣田集輸管網(wǎng)整體優(yōu)化方法[J]. 天然氣工業(yè),2011,31(8):86-89.
[8]潘文超.果蠅最佳化演算法[M].臺(tái)灣:中國(guó)滄海書局,2011.
[9]商冠琪.枝狀管網(wǎng)布局優(yōu)化中的3類問(wèn)題[J].化工機(jī)械,2014,41(3):342-344.
[10]鄭清高.油氣集輸管網(wǎng)幾何布局研究[J].石油學(xué)報(bào),1995,15(1):141-143.
[11]董武成.地面集輸管網(wǎng)優(yōu)化探討[J].科學(xué)管理,2016(2):254.
[12]何緒蕾.關(guān)于油田地面集輸管網(wǎng)優(yōu)化設(shè)計(jì)研究[J].能源與節(jié)能,2015(2):6-7.
[13]羅葉新,張宗杰,王喜,等.油田地面技術(shù)系統(tǒng)布局優(yōu)化模型[J].油氣儲(chǔ)運(yùn),2014,33(9):1004-1009.
[14]劉恩斌,彭善碧,李長(zhǎng)俊,等.基于遺傳算法的天然氣集輸管網(wǎng)參數(shù)優(yōu)化設(shè)計(jì)[J].管道技術(shù)與設(shè)備,2004(4):1-3.
[15]劉揚(yáng).具有確定網(wǎng)絡(luò)拓?fù)潢P(guān)系的集輸管網(wǎng)系統(tǒng)布局優(yōu)化設(shè)計(jì)[J].石油工程建設(shè),1990(3):7-9.
[16]魏立新,劉揚(yáng).油氣集輸系統(tǒng)障礙拓?fù)洳季謨?yōu)化設(shè)計(jì)方法[J].石油學(xué)報(bào),2006,27(6):120-124.
[17]孟榮章,李書文,湯林.大型氣田集輸管網(wǎng)布局優(yōu)化[J].石油規(guī)劃設(shè)計(jì),1998(2):16-18.
[18]陳坤明,簡(jiǎn)朝明,劉松泉,等.單親遺傳和深度優(yōu)先搜索算法的集輸管網(wǎng)優(yōu)化[J].油氣田地面工程,2012,31(8):34-35.
[19]周軍,李曉平,鄧濤,等.集輸系統(tǒng)優(yōu)化設(shè)計(jì)研究的體系結(jié)構(gòu)與發(fā)展方向[J].油氣儲(chǔ)運(yùn),2014,33(7):707-713.
[20]韓建增,汪玉春.集油管網(wǎng)優(yōu)化設(shè)計(jì)研究[J].西南石油學(xué)院學(xué)報(bào),1999,21(3);52-55.
[21]魏立新,姚春雪,馬汝彥,等.稀油集輸系統(tǒng)能耗分析與節(jié)能改造[J].當(dāng)代化工,2019,48(6):1305-1310.

