基于機構拓撲結構的懸臂式掘進機空間位姿偏差分析

方立霞，王 彤，李一鳴，吳 淼

(1.中國礦業大學(北京) 機電與信息工程學院，北京 100083; 2.中國礦業大學銀川學院 信息工程學院，寧夏 銀川 750011; 3.北京信息科技大學 機電工程學院，北京 100101)

據國家能源局2018年統計，我國主體能源的原煤產量高達35.5 億t[1]，且90%為井工開采，故需要大量掘進巷道。盡管綜合機械化掘進量(綜掘)逐年大幅提高，但始終無法跟上綜采的速度，造成“掘采失調”矛盾日益加劇[2]。同時，綜掘工作面環境(高溫、高濕、高塵等環境因素與冒頂、片幫等安全因素的交互作用)惡劣、作業過程中復雜多變的煤巖情況[3]等因素嚴重制約了無人化、智能化精準綜掘的進展。因此，研究并精確掌控掘進作業中機身位姿響應規律，對巷道成形質量與掘進效率的提高，乃至實現智能化自動采掘最終達到“無人化”綜掘，具有實質性的價值和意義。

目前，掘進機位姿方面國內外已有相關研究:SHAFFER GK等[4]建立了掘進機工作機構參數與巷道斷面尺寸之間的數學模型;李軍利等[5]將掘進機簡化為履帶式機器人，將視其為一系列連桿通過運動副關節串聯而成的開式運動鏈,建立了關節空間和驅動空間的運動學方程，求出末端截割臂的位姿矩陣;田劼等[6]提出懸臂式掘進機的空間位姿運動學模型，采用DH算法，利用雅克比矩陣建立了懸臂式掘進機機身及截割頭空間位姿坐標變化矩陣，從而得到了截割頭空間運行軌跡;田原等[7]利用機器視覺技術檢測攝像機與激光指向儀之間的相對空間位姿，通過空間矩陣變換計算出掘進機機身相對指向激光的空間位姿參數。以上研究提供了掘進機空間位姿的運動學推導思路，但局限于對掘進機位姿偏差研究提供理論分析思路，缺少對掘進機在實際復雜變載工況下產生位姿偏差的實時動態分析，且分析方法為多解析法，采用數學方法推導，存在消元過程復雜、計算量大的弊端。基于此，宗凱等[8]建立了懸臂式掘進機橫向截割機身位姿動力學耦合模型，僅以對巷道成形質量產生較大影響的機身臥底量及機身俯仰角為重點目標研究其對機身位姿的影響，為懸臂式掘進機智能化自主糾偏提供了導向依據;張敏駿等[9]對懸臂式掘進機支撐機構進行了力學分析，建立了仰俯位姿偏差與執行機構運動數學模型，提出基于模糊神經網絡PID控制的俯仰位姿智能控制算法，但缺少考慮動載荷對空間位姿偏差的影響分析。

綜上可知，目前考慮實際變載工況下懸臂式掘進機全方位空間位姿偏差的綜合分析及相關工作研究較少，故筆者基于EBZ160型懸臂式掘進機機械結構的拓撲結構分析，建立了懸臂式掘進機空間并聯行走/支撐機構可補償仰俯角、橫滾角、巷頂距偏差的數學模型，截割串聯機構可補償水平偏向角、水平偏距及車前距偏差數學模型;利用空間機構正/逆解思想，正解求解已知各機構回路幾何結構參數時機身的空間位姿偏差;逆解推導對應空間極限位姿偏差時各驅動回路的幾何結構參數，以驗證該模型的準確性。結合本項目組陶云飛等[10]掘進機位姿激光自動測量法提供的掘進機實時空間位姿信息,可實現為懸臂式掘進機的智能化實時位姿糾偏提供準確依據。

1 懸臂式掘進機拓撲結構分析及空間位姿偏差

根據機構拓撲結構分析EBZ160懸臂式掘進機空間拓撲結構簡圖如圖1所示,其機械結構采用空間混聯結構形式:下部分為由機身/行走機構-前鏟板四連桿液壓回路-后支撐四連桿液壓回路共同組成的掘進機行走/支撐空間并聯機構，該結構形式不僅可增強掘進機機身整體的剛度，還可保證在較大的沖擊截割載荷下整機的平穩性及保障空間位姿糾偏的有效實施;上部分結構為由截割臂水平回轉回路-截割臂升降回路共同組成的截割串聯機構，該結構形式可保障執行部件具有較大工作空間的優勢[11]。

實際作業過程中，復雜多變的截割工況導致懸臂式掘進機機身偏離預設掘進規劃路徑，從而產生空間位置和姿態偏差，即空間位姿全偏差W(W=[α,β,γ,A,L,H]T)，各空間位姿偏差描述及影響見表1[12]。位姿偏差的存在對巷道的成型及質量產生極大的影響，大大制約了智能化精準掘進的進展與實施,故本文將從空間機構拓撲學角度對其空間位姿偏差展開詳細分析研究。

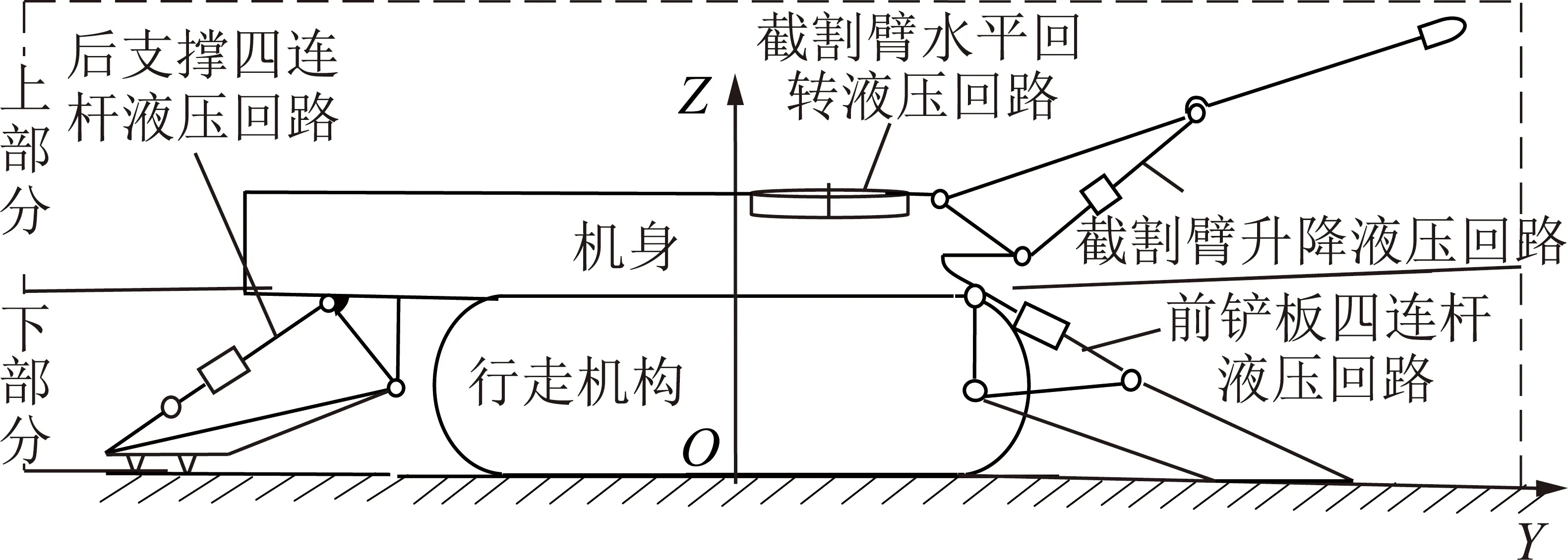
圖1 懸臂式掘進機結構分析示意Fig.1 Structural analysis sketch of cantilever roadheader

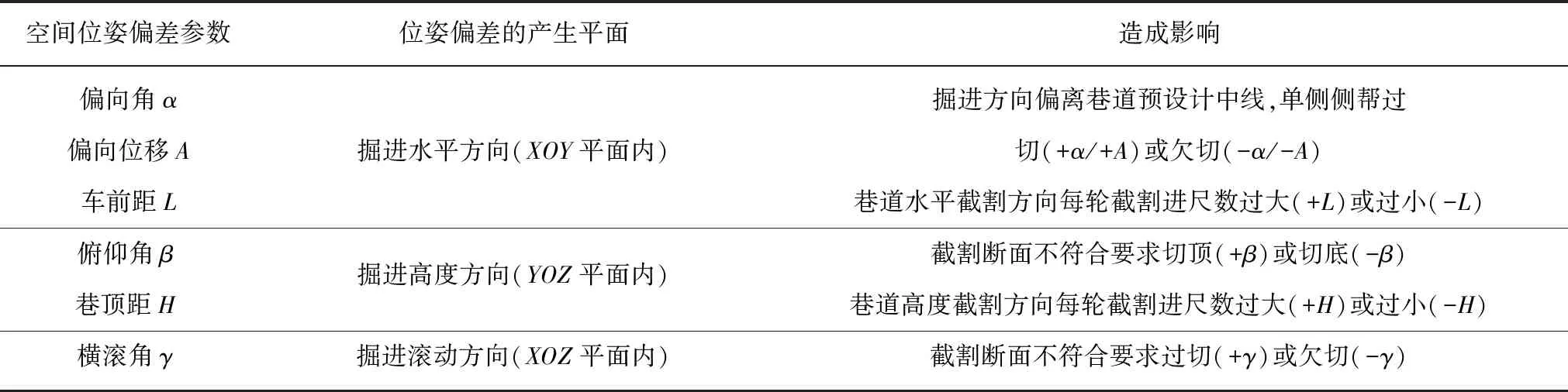
表1 懸臂式掘進機空間機身位姿偏差描述及影響Table 1 Description and effect of spatial posture deviation for cantilever roadheader

2 基于懸臂式掘進機位拓撲結構分析的空間位姿偏差數學模型構建

基于懸臂式掘進機空間拓撲結構,本節將對其下部分(行走/支撐并聯機構)和上部分(水平回轉回路和截割臂升降回路機構)各自產生的空間位姿偏差進行數學模型的構建。

2.1 行走/支撐并聯機構拓撲結構分析

依據以上對EBZ160懸臂式掘進機空間結構采用空間分析，在掘進工作面(掘進高度方向YOZ平面、掘進滾動方向XOZ平面)搭建其行走/支撐機構空間并聯機構模型[13-14]如圖2所示。該機構主要由前鏟板/后支撐與機身上旋轉鉸接點Ri3構成的動平臺{R13-R23-R33-R43}(機身平面)、前鏟板(后支撐)與巷道底部靜接觸點Fi構成的靜平臺{F1,F2,F3,F4}和4條SOCi(Single Open Chain)({-Ri1⊥Pi2‖Ri1-Fi-},i=1,2,3,4)單開鏈共同構成,其中,Pi2為前鏟板/后支撐液壓油缸平移鉸鏈;Ri1為前鏟板(后支撐)液壓油缸下鉸接點[15]。對應單開鏈及動、靜平臺共同組成空間POCi(Per Open Circuit)并聯回路(i=1,2,3,4):

POC1回路:{-F3-R31⊥P32‖R33-R23⊥P22‖

R31-F2-};

POC2回路:{-F2-R21⊥P22‖R23-R13⊥P12‖

R11-F1-};

POC3回路:{-F1-R11⊥P12‖R13-R43⊥P42‖

R41-F4-};

POC4回路:{-F4-R41⊥P42‖R43-R33⊥P32‖

R31-F3-}。

圖2中，l1,l2，l3，l4分別為前鏟板/后支撐所在單支鏈SOCi的邊長，mm;δ為后支撐支鏈與巷道底部夾角，(°)。

構建掘進機仰俯角偏差+β時的空間位姿結構模型如圖3所示(為方便計算推導將SOC1和SOC2單支鏈分別沿X軸對稱平移)。以靜平臺中心為坐標系原點建立靜坐標系O-XOY，坐標系Y軸方向與實際掘進方向保持一致;以動平臺中心為坐標系原點建立動坐標系p(o)-xoy。

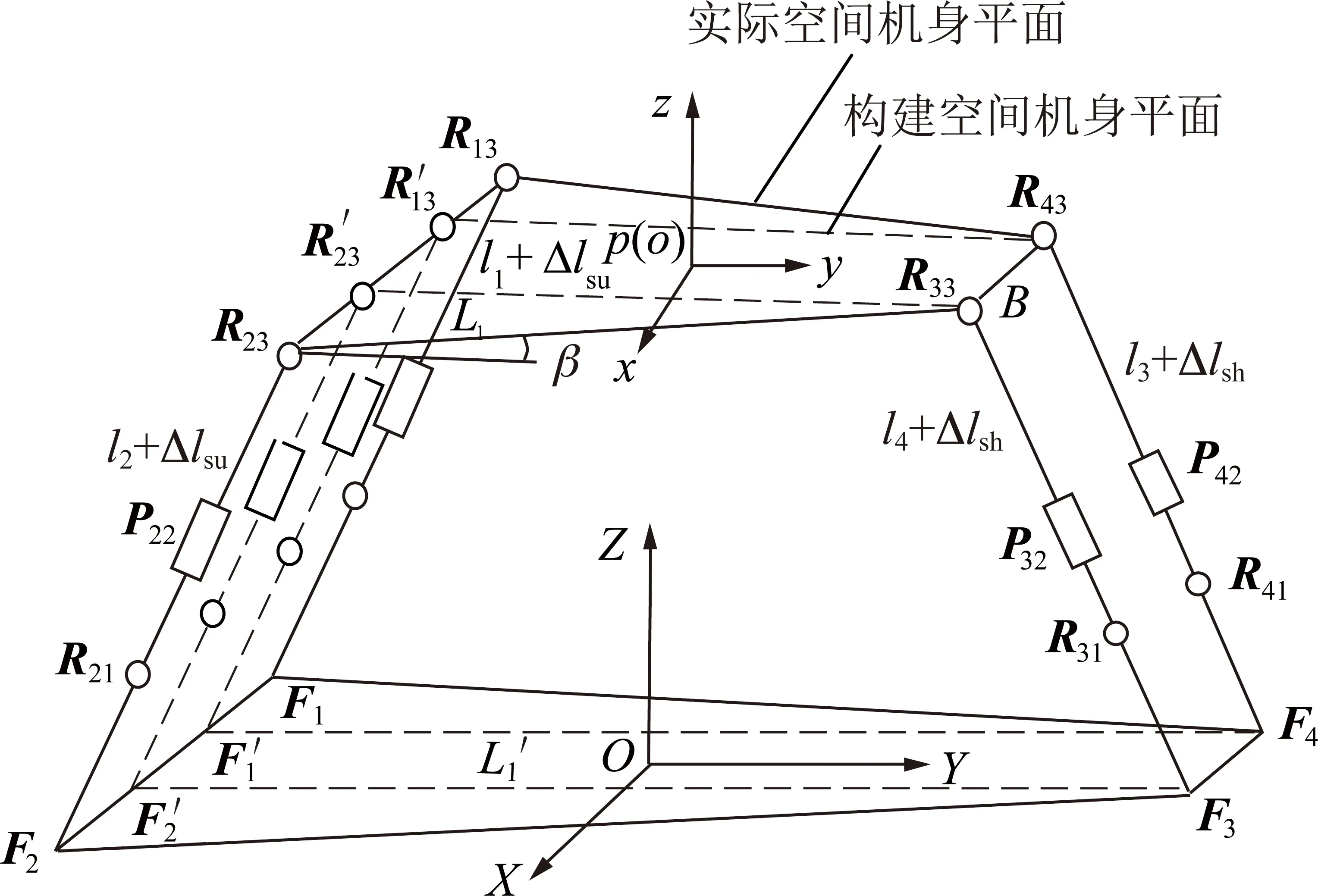
圖3 仰俯誤差時行走/支撐空間并聯機構模型Fig.3 Spatial parallel structural model of walking/supporting mechanism with pitching error

圖3中，L1為機身長度(R′13R43=R′23R33=L1);L′1為前鏟板/后支撐與巷道接觸點間的長度(R′23F3=R′13F4=L′1);B為機身實際寬度(R′13R23=R33R43=F′1F′2=F3F4=B)。

POC1回路中，動坐標系中的動鉸接點R′23,R33及靜坐標系中的固定點F′2和F3相對靜坐標系的坐標[15]分別為

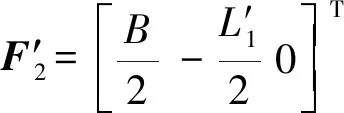
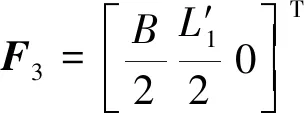
(1)

式中，Δlsu為后支撐液壓油缸長度調節變化量。

2.1.1機身仰俯偏差β數學模型的建立

組成POC1回路的兩條單開支鏈SOC2和SOC3滿足約束方程:

Zp=(l2+Δlsu)sinδ+(L1sinβ)/2

式中，xp,yp,zp分別為動坐標系原點相對于靜坐標系原點的X，Y，Z方向的坐標。

則:

R33F3=

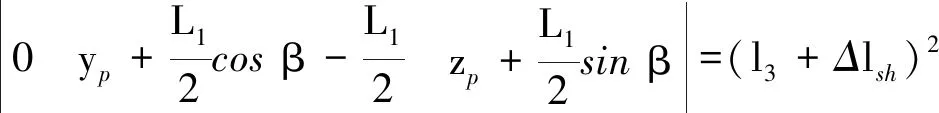
(2)

式中，Δlsh為前鏟板液壓油缸調節變化量。

將式(2)代入約束方程式得

[(l2+Δlsu)cosδ+L1cosβ-L′1]2+

[L1sinβ+(l2-Δlsu)sinδ]2=(l3+Δlsh)2

(3)

為簡化表達,設a=(l2-Δlsu)cosδ-L′1，最終得機身動平臺相對巷道底部靜坐標系的仰俯角偏差β數學模型:

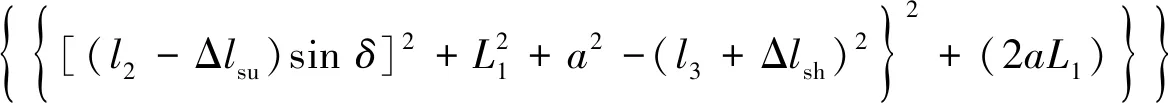
(4)

利用MATLAB對機身仰俯角偏差β與前鏟板液壓油缸調節變化量Δlsh和后支撐的液壓油缸調節量Δlsu間的關聯性進行解算，結果如圖4所示。

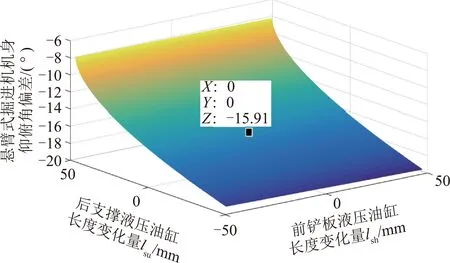
圖4 仰俯角偏差與前/后支撐液壓油缸長度變化關系Fig.4 Diagram between front/rear support hydraulic cylinder and pitch deviation

由圖4懸臂式掘進機仰俯角偏差與前/后支撐液壓油缸長度變化關系曲線解算結果可知，機身仰俯角β與前鏟板液壓油缸長度變化Δlsh和后支撐的液壓油缸長度變化Δlsu之間呈空間微弧狀曲面變化規律。

為定性研究前鏟板和后支撐兩者分別對機身仰俯角偏差的影響程度，設定前鏟板和后支撐液壓油缸調節變動量均為[-48.5 mm,48.5 mm]，用Matlab進行解算。如圖5(a)所示，設定范圍內，保持后支撐液壓油缸變動量Δlsu=0恒定，由前鏟板液壓油缸變動引起的機身仰俯角偏差βsh呈空間微弧狀曲線變化趨勢，對應βsh變動范圍為:-4.409°≤βsh≤2.593°;同理，如圖5(b)所示，設定范圍內，保持前鏟板液壓油缸調節量Δlsh=0恒定，后支撐液壓油缸長度變動引起的機身仰俯角βsu亦呈空間弧狀曲線規律變化，對應βsu變動范圍為:-6.941°≤βsu≤4.529°。

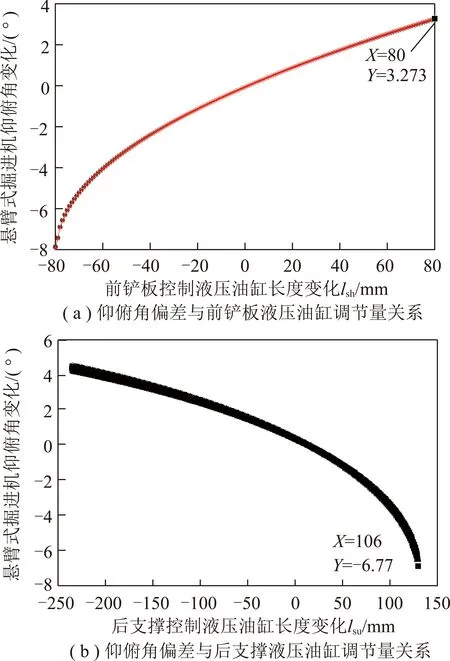
圖5 仰俯角偏差與前鏟板/后支撐液壓油缸調節量關系Fig.5 Relational between front-spade/rear-support hydraulic cylinder and pitch deviation

比較分析結果發現，圖5(a)曲線變化趨勢比圖5(b)曲線變化趨勢平緩，即前鏟板液壓油缸長度變動引起的機身仰俯角變動較后支撐板液壓油缸長度變化引起的機身仰俯角變動要小，說明前鏟板液壓油缸變動量對機身仰俯角的影響程度較小;且在同等變動范圍內，前鏟板液壓油缸對機身仰俯角偏差β變動補償范圍也較小。故實施機身仰俯角糾偏時，可優先考慮采用首先調節后支撐液壓油缸作為粗調，補償粗大仰俯角偏差，而后采用調節前鏟板液壓油缸作為精調節，補償微小仰俯角偏差。

2.1.2機身可補償橫滾角偏差γ數學模型的建立

假設后支撐的移動副P12(P22)和前鏟板的移動副P32(P42)可分別通過調節相對應控制液壓油缸以實現對SOCi支鏈邊長長度li(i=1,2,3,4)的調節，同理，選擇POC2并聯回路得到機身動系相對于巷道靜坐標系的橫滾角偏差γ數學模型:

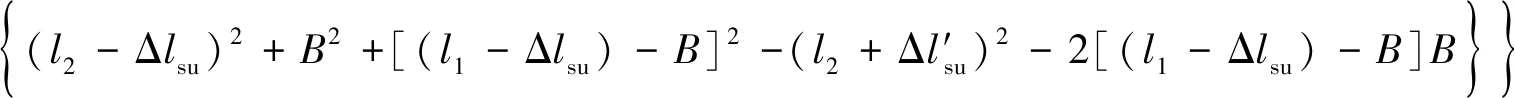
(5)

可補償橫滾角偏差γ與前(后)支撐液壓油缸長度變化關系如圖6所示。

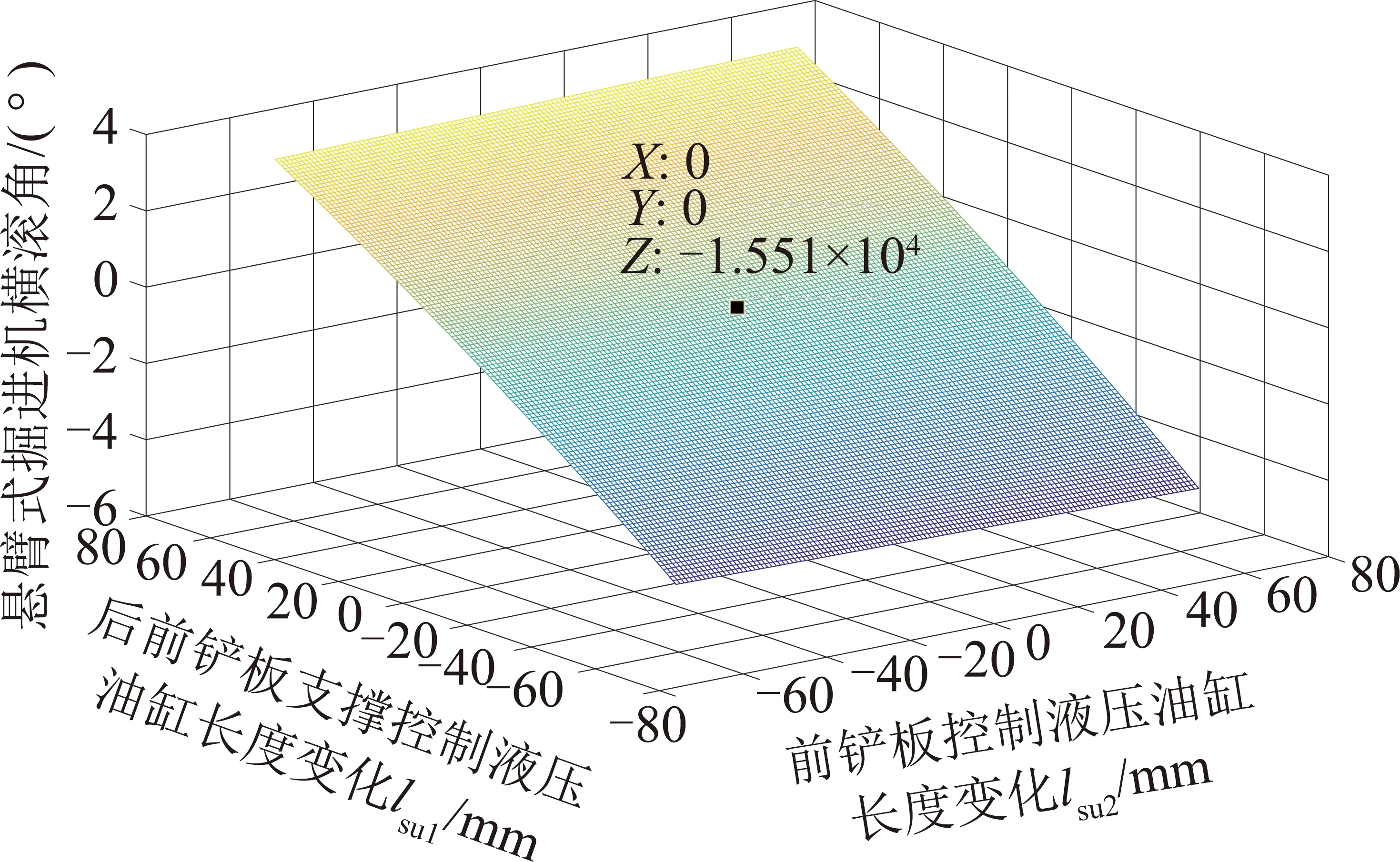
圖6 橫滾角偏差與前(后)支撐液壓油缸長度變化關系Fig.6 Diagram between front/rear support hydraulic cylinder and compensable ±γ deviation

分析結果可知:機身橫滾角γ與前鏟板液壓油缸長度變化Δlsh(后支撐的液壓油缸長度變化Δlsu)間亦呈空間微弧狀曲線變化關系，即當前鏟板液壓油缸(后支撐板液壓油缸)長度變化，機身橫滾角γ隨之發生遞增(遞減)變化(實際工程中，實現分別對兩個前鏟板(后支撐)的液壓回路控制，則會增大整機的液壓回路復雜度)。

2.1.3巷頂距偏差±H的推導解算

截割過程中由于掘進巷道底部不平以及截割載荷的變動造成機身產生巷道高度方向的巷頂距偏差±H。選擇POC1和POC3并聯回路,通過同步控制調節液壓回路邊長(即同步等量控制前鏟板液壓油缸和后支撐液壓油缸變動量)，可實現對巷頂距偏差的補償:

H=±(Zp-H0)

(6)

式中，H0為機身動坐標系的起始高度(H0=858.81 mm);Zp為機身動點的Z坐標值。

巷頂距偏差±H的變化曲線如圖7所示。 分析圖7仿真曲線可知:同步調節前鏟板(后支撐)液壓油缸變動量(Δlsh=Δlsu)，可補償一定量的巷頂距偏差，且液壓油缸調節變動量與可補償的巷頂距偏差兩者之間符合對應線性關系。

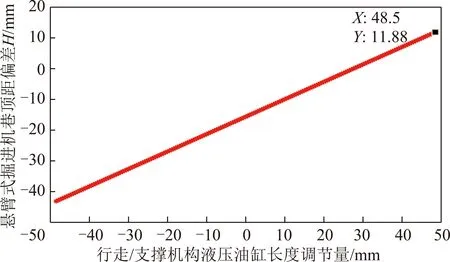
圖7 機身巷頂距與前/后支撐液壓油缸長度變化曲線Fig.7 Relational curve of between roof distance and front/back support hydraulic cylinder

至此，綜合式(6)～(8)，得到機身上任意測量動點[xp,yp,zp]相對巷道底面靜平臺坐標系產生的可補償仰俯偏差(±β)、橫滾角偏差(±λ)和巷頂距偏差(±H)的數學模型。

2.2 水平回轉回路和截割臂升降回路機構拓撲結構分析及對應位姿偏差數學模型建立

截割過程中，隨機變化的截割載荷是掘進機機身空間位姿偏差產生的重要因素之一，很多文獻對截割載荷都有研究,該動載荷在截割平面內可分解為Fx，Fy和Fz三個方向的分力[20-22]:

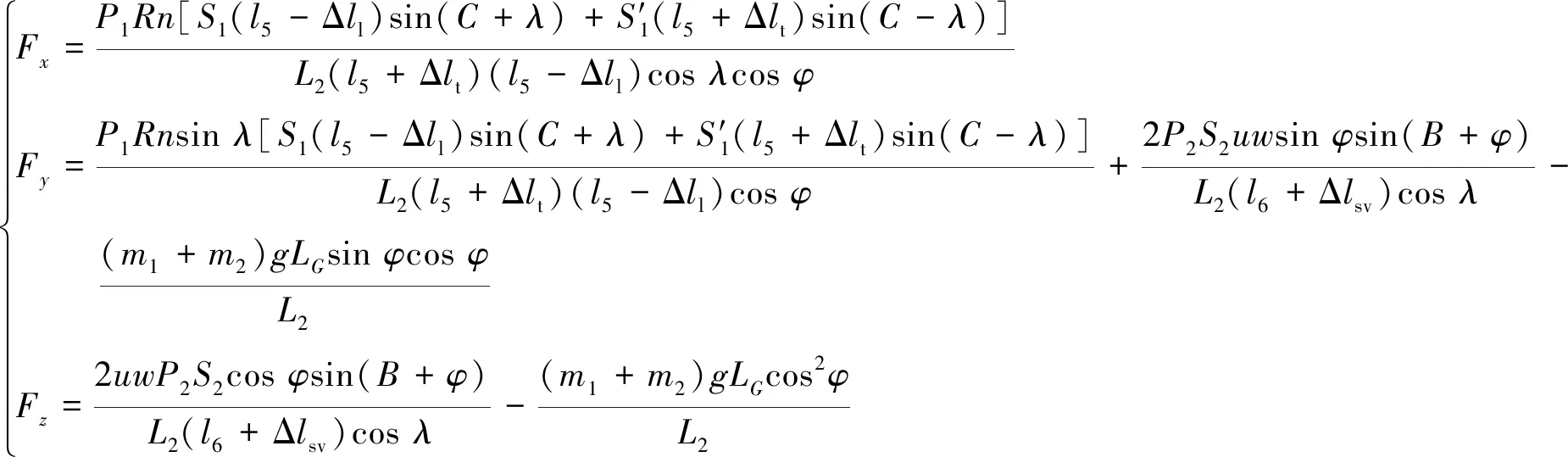
(7)

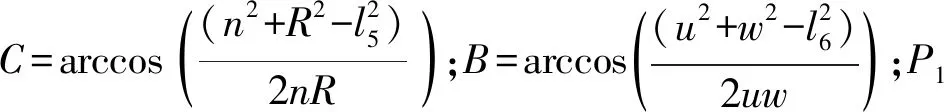
分析式(7)發現:空間截割載荷不僅與掘進機本體幾何結構參數、截割工況相關聯，同時亦與截割過程中截割臂水平轉角和升降擺角存在對應關系。故同理以截割機構的拓撲結構為分析基礎，分別對截割機構中的截割臂回轉和升降回路進行拓撲結構研究，進而對其在掘進水平面(XOY)的位姿偏差展開研究。

2.2.1水平回轉回路和截割臂升降回路機構拓撲結構分析

(1)懸臂式掘進機截割機構水平回轉并聯回路拓撲結構分析。截割機構水平回轉并聯回路的拓撲結構如圖8所示，圖中,R53和R63分別為截割臂回轉油缸與機身旋轉鉸接點;P52和P62分別為回轉油缸移動副;R73和R83分別為回轉油缸與回轉臺旋轉鉸接點;R3為回轉臺與機身旋轉鉸接點。

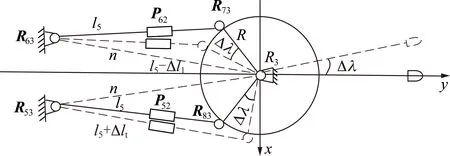
圖8 懸臂式掘進機截割水平回轉并聯機構Fig.8 Horizontal rotary loop for cutting mechanism of cantilever roadheade

截割臂水平回轉并聯回路POC5由兩條單開鏈組成，對應方位特征集Msh1和Msh2[18-20]為

式中,ρ53,ρ63,ρ73,ρ83為鉸接點R53,R63,R73,R83到回轉圓臺旋轉基點的徑矢;ti,ri為第i個有限移動和轉動(i=0,1,2,3)。

由并聯機構拓撲結構綜合[17]可知POC5回路方特集Msh為

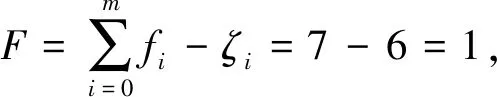
為簡化表達設:q=(l5+Δll)cosθ-h，推導出POC5并聯回路輸出截割臂水平回轉轉角Δλ為

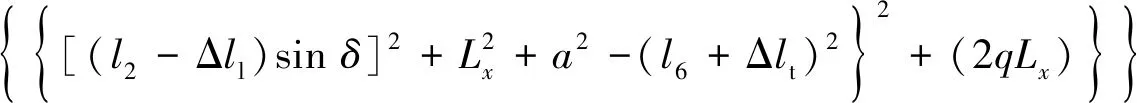
(8)

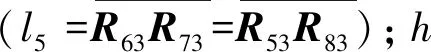
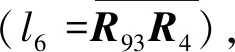
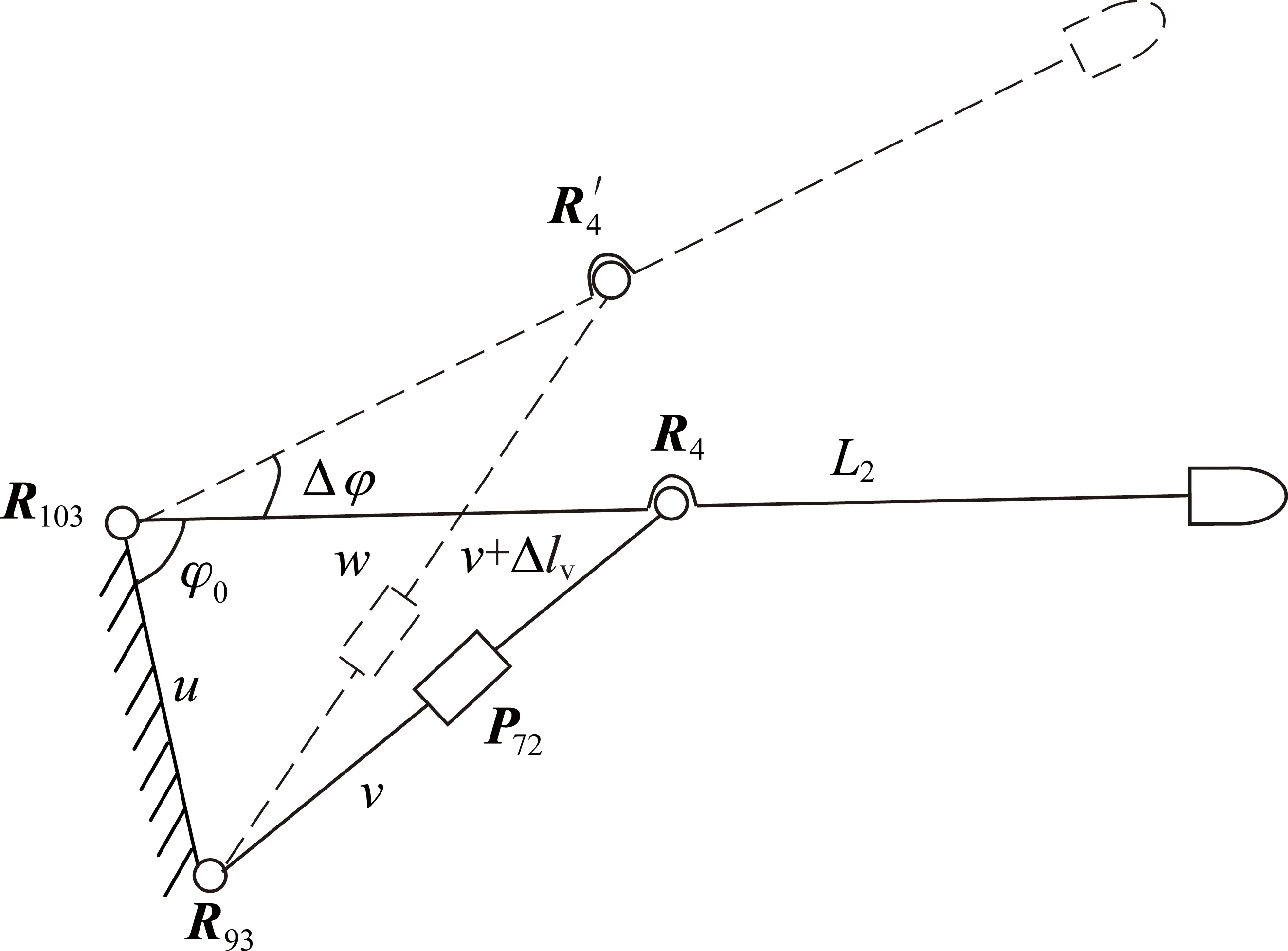
圖9 截割臂升降機構回路Fig.9 Lifting-loop structure of cutting-arm

圖9中，R93和R103分別為截割臂與機身旋轉鉸接點;P72為截割臂升降液壓油缸移動副;R4為截割臂升降液壓油缸與截割臂旋轉鉸接點。

由串聯機構拓撲結構綜合[15]可知截割臂升降機構回路POC6方特集Msv為

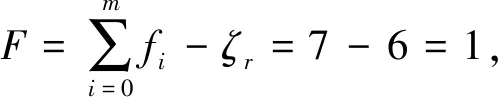
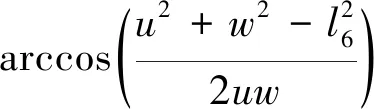
(9)

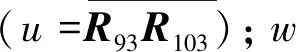
2.2.2水平回轉回路和截割臂升降回路機構及對應位姿偏差數學模型建立

(1)偏向角α和水平偏距A偏差數學模型建立。截割頭承受的動態截割載荷最終作用至掘進機機身動坐標系p-xoy，將對機身同時產生一定力F′x和轉矩M′x的作用，使得機身產生相對巷道底部的運動趨勢，超過摩擦極限Ffmax時,機身將偏離預設截割軌跡，產生水平偏距A和偏向角α偏差，反之機身處于平穩狀態。

① 當等效轉矩MFx≥MFfmax時(Mx=FxL2)，機身將會產生水平偏角α，根據功能守恒定理得

整理得機身水平偏角α的數學模型為

Δll)cosλcosφ]/{πL′1P1Rn[S1(l5-Δll)×

sin(C+λ)+(l5+Δlt)S′1sin(C-λ)]}

(10)

② 當等效轉換力F′x≥Ffmax時，機身將產生水偏距A。根據能轉換守恒關系:

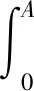
整理并將上述截割載荷Fx、截割臂水平回轉角Δλ及升降擺角Δφ代入，得機身水平偏距A偏差的數學模型為

Δll)cosλcosφ]/{4P1Rn[S1(l5-Δll)×

sin(C+λ)+(l5+Δlt)S′1sin(C-λ)]}

(11)

式中，M為懸臂式掘進機整機質量(包括截割頭質量(m1)、截割臂質量(m2)、機身和行走(支撐)部質量(m3));μ為機身與巷道底部的摩擦因數,μ=0.8～1.0[15]。

(2)機身車前距偏差±L數學模型建立。掘進機機身空間車前距偏差±L主要是由截割載荷Fy及Fz產生,根據力學平衡關系可知:當Fysinφ≥Ff時，產生車前距偏差±L。

根據功能轉換平衡定律:

整理得FysinφL=μL1(Mg+Fzcosφ)/2,最終得車前距偏差的數學模型為

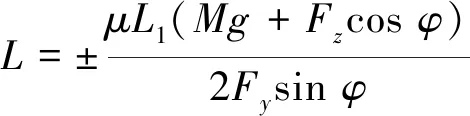
(12)

綜合式(10)～(12)可知,懸臂式掘進機在水平掘進面內產生的水平偏角、水平偏距及車前距偏差不僅與掘進機本身相關幾何結構參數、截割動態載荷相關聯，同時亦與掘進機截割臂截割過程中的姿態(截割臂水平轉角和升降擺角)相關聯。

綜上對懸臂式掘進機在截割過程中產生的空間動態位姿偏差W=[α,β,γ,A,L,H]T的各偏差因素的定性分析，建立了截割過程中各截割空間的空間位姿偏差的數學模型，并對各位姿偏差的變化規律展開分析研究。分析結果表明:機身仰俯角偏差、橫滾角偏差、巷頂距偏差與掘進機行走/支撐機構相關聯，故可通過調節相應行走/支撐機構回路的結構參數進行相對應粗細偏差的補償;而水平偏角、水平偏距及車前距偏差則與動態截割載荷及截割臂的位姿狀態相關聯，故可通過實時動態調整截割臂的位姿狀態來補償相應的偏差。此結論將為智能化懸臂式掘進機實時動態精準糾偏提供有效的實施依據。

3 懸臂式掘進機位姿偏差正/逆解分析

已知EBZ160實體幾何參數:L1=3 627.21 mm,L′1=7 352.34 mm,L2=3 900 mm,LG=1 750 mm,l1=l2=1 487.54 mm，l3=l4=2 637.87 mm,l5=1 662.08 mm,l6=1 370.86 mm,B=1 855 mm，R=844 mm，m1=1 600 kg,m2=5 700 kg,M=4.5 t以及各單支鏈回路邊長li(i=1,2,3,4)(由GUC1000液壓油缸位移傳感器[22]測出)，直接代入位姿正解計算公式(4)～(12)，避免了復雜數學矩陣解析方法，直接得到機身動平臺的坐標相對于巷道底面靜坐標系的位置及位姿偏差及可補償空間位姿偏差的極限范圍，見表2。

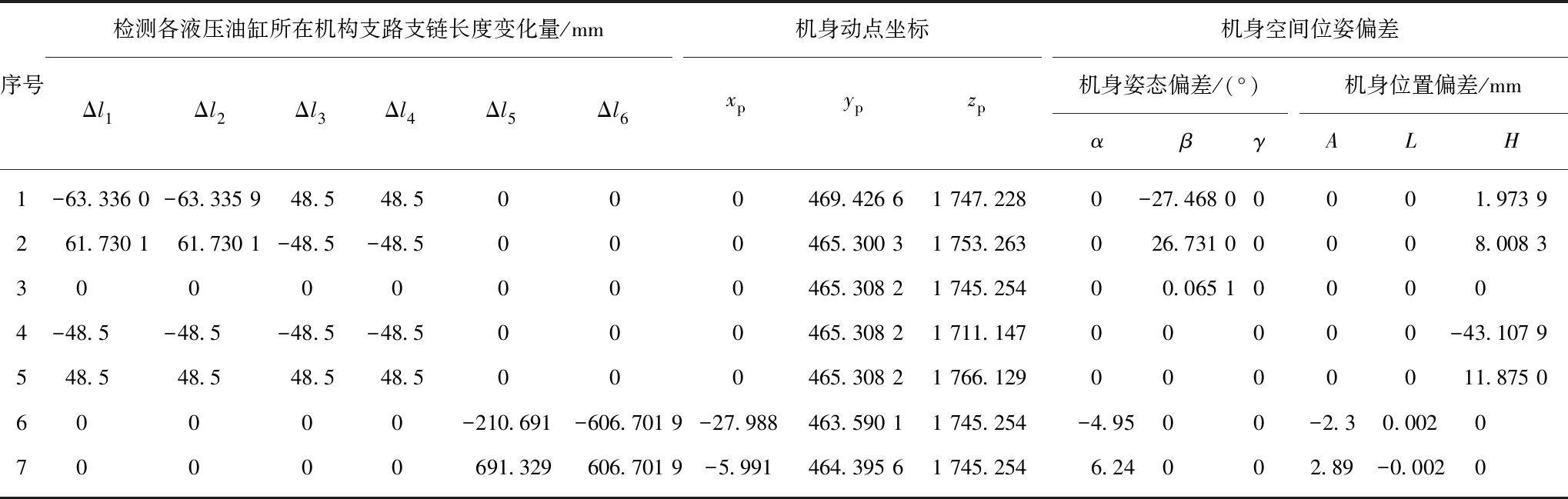
表2 懸臂式掘進機拓撲結構正解分析Table 2 Forward solution for topological structure analysis of cantilever roadheade

(1)由表2中1,2行正解信息可知:通過調節前鏟板液壓油缸Δlsh∈[-63.335 9 mm,63.730 1 mm]和后支撐液壓油缸ΔLsu∈[-48.5 mm,48.5 mm]，可實現補償機身空間仰俯誤差的范圍為:β∈[-27.468°,26.731°]。

(2)由表2中3行正解信息可知:當各回路液壓油缸不發生變化時，機身動點的起始坐標為[xp,yp,zp]=[0,465.308 2,1 745.254 4]。

(3)由表2中4,5行正解信息可知:當同步調節前鏟板和后支撐液壓油缸長度時(Δlsh=Δlsh∈[-48.5 mm,48.5 mm])，可補償機身巷頂距偏差范圍為:H∈[-43.107 9 mm,11.875 3 mm]。

(4)由表2中6,7行正解信息可知:當水平回轉液壓油缸長度(Δlt∈[-606.701 9 mm,606.719 mm])并同步調節截割臂豎直升降液壓油缸長度(Δlv∈[-210.691 mm,691.328 7 mm])，可實現動態補償機身水平偏角偏差范圍為:α∈[-4.95°,6.24°]。

同理，根據機構的空間拓撲結構可知機構位姿偏差的逆解可歸結為:已檢測到機身動平臺的位姿[21-22]信息[xp,yp,zp],反求對應該位姿時各液壓油缸所在支鏈回路邊長li(i=1,2,3,4)，即

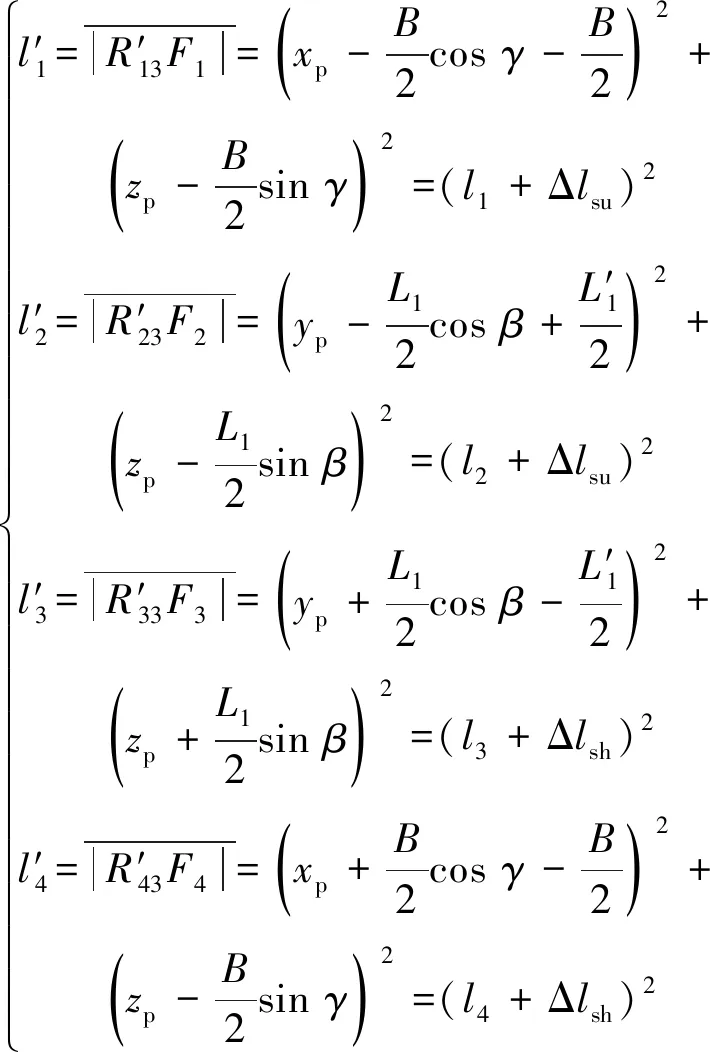
(13)

同理，根據YHJ001型機載激光測距儀測量機身提供的機身實時位置信息[23]，代入逆解求解式(13)，可方便快捷得到掘進機對應的結構參數逆解結果(各液壓回路邊長li(i=1,2,3,4)),見表3。

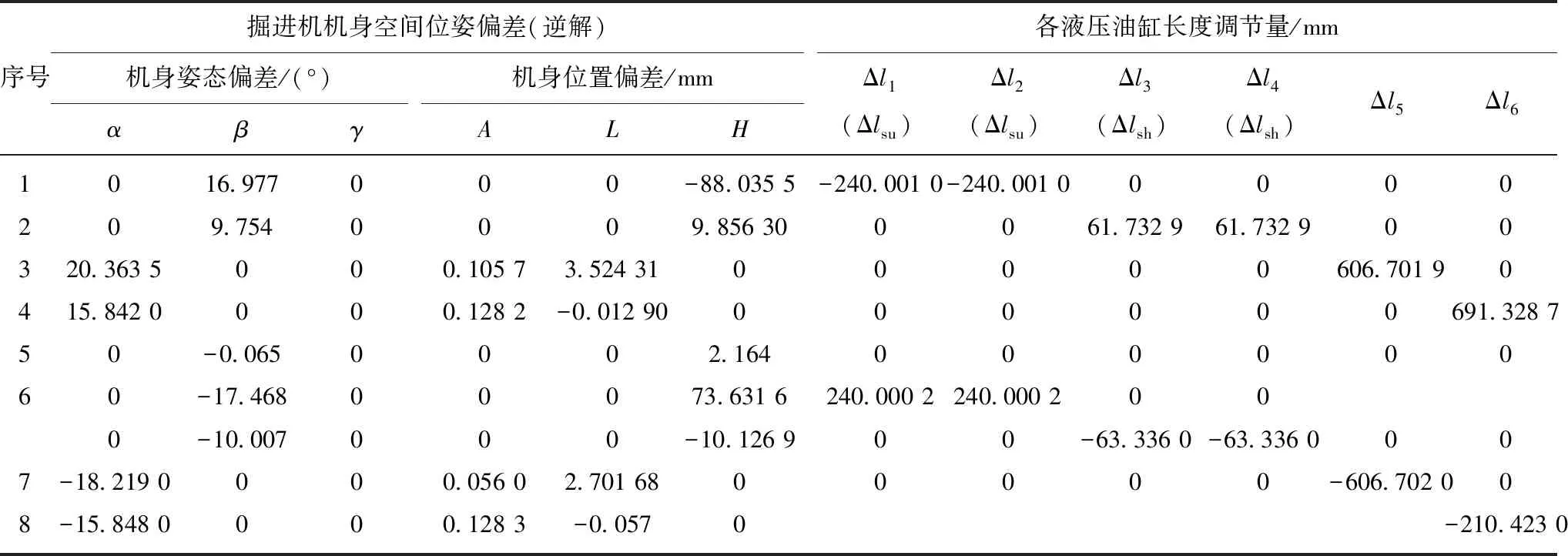
表3 懸臂式掘進機拓撲結構逆解分析Table 3 Inverse solution for topological structure analysis of cantilever roadheade

分析表3中的逆解數據:

(1)實際EBZ160懸臂式掘進機設計工作條件:前鏟板下向上抬起340 mm，向下臥底260 mm，即要求前鏟板液壓油缸的理論調節范圍為:-63≤ΔLsh≤62，設計選配的后支撐液壓油缸理論調節量為:-240≤ΔLsu≤240。根據表3逆算結果，機身仰俯角偏差β在[-27.468°,26.731°]的變動范圍內:前鏟板液壓油缸實際變動量Δlsh為[-63.336 mm,61.732 9 mm]，后支撐液壓油缸實際變動量Δlsu范圍為[-240.000 2 mm,240.001 mm]，即逆解計算出對應液壓油缸實際變動量Δli≤10-2(i=1,2,3,4)，滿足工程設計要求，從而驗證了本文所提供的位姿逆解的正確性。

(2)同理，要求截割臂截割范圍:高度4.8 m，寬度5.4 m，可知回轉液壓油缸理論變動范圍量ΔL5為[-607 mm,607 mm];截割臂升降液壓油缸變動量ΔL6范圍為[-210 mm,691 mm]。根據本文推導出水平偏角α在[-34.067°,36.205 5°]的可補償變動范圍內，逆推導出回轉液壓油缸實際變動范圍量Δl5為[-606.701 9 mm,606.701 9 mm];截割臂升降液壓油缸實際變動量Δl6范圍為[-210.422 8 mm,691.329 mm]，即逆解計算出對應液壓油缸實際變動量偏差均滿足Δli≤10-2(i=5,6)，亦驗證了本文所提供的位姿逆解完全滿足工程要求。

4 實驗驗證及仿真分析

為驗證本文推論的可實踐性，以EBZ160懸臂式掘進機為實驗基體，將實驗設備(表4)分別安裝在標定的掘進機機身轉盤中心位置，沿掘進前進方向 20～60 m長度內，每隔10 m模擬在截割頭施加恒定瞬間截割動載荷，采集并記錄測量懸臂式掘進機機身姿態偏差數據信息并進行數據處理[23]。

將測量解算出的懸臂式掘進機機身質點的空間位姿偏差信息數據代入逆解公式(13)即可求解出相應糾偏液壓回路邊長Δli，將逆解結果反饋給控制液壓回路實施實時空間位姿偏差調節。利用MATLAB對糾偏前后的實驗測量數據進行軌跡曲線進行擬合，如圖10所示。

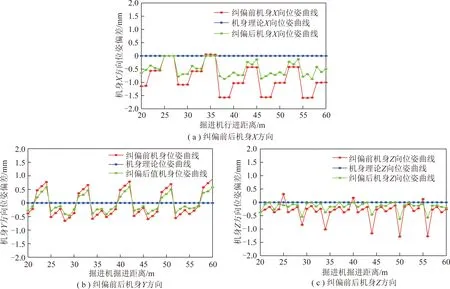
圖10 糾偏前后掘進機空間位姿偏差變化曲線Fig.10 Spatial deviation curves of cantilever roadheader before and after rectification

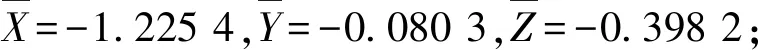
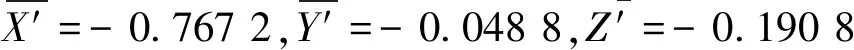
均方差為

Sx′=-0.767 2，Sy′=0.295 4，Sz′=-0.190 8

實驗統計數據表明:隨測量距離的增大，機身空間各方向的動態位姿偏差亦呈隨機遞增趨勢，但經過本方案對機身進行相應糾偏調節之后，機身的空間位姿偏差不論從穩定性和實施結果上來講都得到顯著改善。

5 結 論

(1)基于懸臂式掘進機的結構分析，首次提出懸臂式掘進機機身空間全方位位姿偏差W=[α,β,γ,A,L,H]T，實現了懸臂式掘進機空間全方位各項位姿偏差的定性描述;并提出通過結合空間機構的拓撲結構思想來定性分析和研究懸臂式掘進機結構特性及機身空間全方位位姿偏差。

(2)基于懸臂式掘進機的拓撲結構分析，分別建立了行走/支撐機構在掘進平面、掘進高度平面內產生的各項相關位姿偏差的數學模型，通過縮減數學模型分析可知:調節前鏟板/后支撐液壓油缸驅動量，可實現補償機身最大仰角偏差26.731°，最大俯角偏差27.468°，可補償最大巷頂距偏差20.253 7 mm;同時，通過動態實時調整截割臂截割姿態，可補償機身最大水平偏角偏差36.067°。從而實現了對懸臂式掘進機空間全方位位姿偏差的定性分析和定量分析，同時也為懸臂式掘進機的實時糾偏提供了準確分析數學模型和依據。

(3)利用空間機構正/逆解思想，正解通過各機構回路支鏈的幾何結構信息求解出動平臺位姿偏差信息及可補償空間位姿;通過檢測動平臺的位姿信息逆解求解出對應該位姿時懸臂式掘進機的相關幾何結構參數信息，最后通過實驗結合軟件仿真分析糾偏前后的空間位姿偏差，結果表明:經本方案糾偏后的各項空間位姿偏差的均方差大大降低，進一步驗證了利用空間機構拓撲結構分析懸臂式掘進機空間位姿偏差的準確性和可行性。