談如何破解非常規邊界磁場問題
———緣起2020年全國高考理綜卷Ⅰ第180題

◇ 河北 李春亞

2020年教育部考試中心發布《中國高考評價體系》,在評價理念上實現了由傳統的“知識立意”“能力立意”評價向“價值引領、素養導向、能力為重、知識為基”綜合評價的轉變.高考評價體系主要由“一核”“四層”“四翼”構成,“四層”中“學科素養”的二級指標“科學思維”要求:采用嚴謹求真的、實證性的邏輯思維方式應對各種問題.能夠根據對問題情境的分析,運用實證數據分析事物的內部結構和問題的內在聯系,以抽象的概念來反映客觀事物的本質特征和內在聯系.運用抽象與聯想、歸納與概括、推演與計算、模型與建模等思維方法來組織、調動相關的知識與能力,解決生活實踐或學習探索情境中的各種問題.2020年高考恰恰是深化課程改革,落實《中國高考評價體系》的有益探索.

帶電粒子在有界勻強磁場中的運動問題歷來是各類考試的重點.該問題很好地考查了帶電粒子在磁場中的圓周運動規律、數學三角函數和幾何知識在物理中的應用能力、分析抽象能力.該問題經常與臨界極值問題聯系,常以選擇題或壓軸題的形式出現.學生不僅要掌握常規邊界磁場問題,還要了解非常規邊界問題.

常規邊界磁場包括單直線邊界、平行線邊界、圓形邊界、三角形邊界、平行四邊形邊界等.

非常規邊界磁場包括不平行兩射線邊界、扇形邊界、多邊形邊界、組合邊界、未知邊界等.

2020年高考全國卷Ⅰ的第18題,就是非常規邊界磁場問題的典型代表題目.

例1(2020年全國卷Ⅰ)一勻強磁場的磁感應強度大小為B,方向垂直于紙面向外,其邊界如圖1中虛線所示為半圓,ac、bd與直徑ab共線,ac間的距離等于半圓的半徑.一束質量為m、電荷量為q(q＞0)的粒子,在紙面內從c點垂直于ac射入磁場,這些粒子具有各種速率.不計粒子之間的相互作用.在磁場中運動時間最長的粒子,其運動時間為( ).

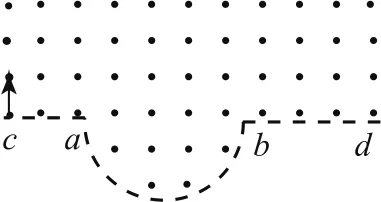
圖1

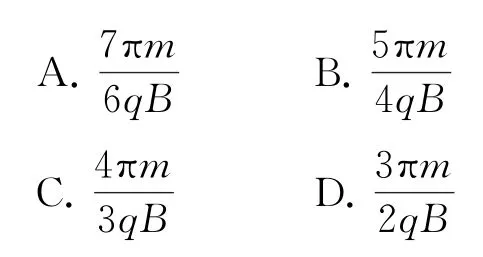
解析

則粒子在磁場中運動的時間與速度無關,軌跡對應的圓心角越大,運動時間越長.粒子垂直ac射入磁場,則軌跡圓心必在ac直線上,將粒子的軌跡半徑由零逐漸放大.(對應圖2中①②③軌跡)

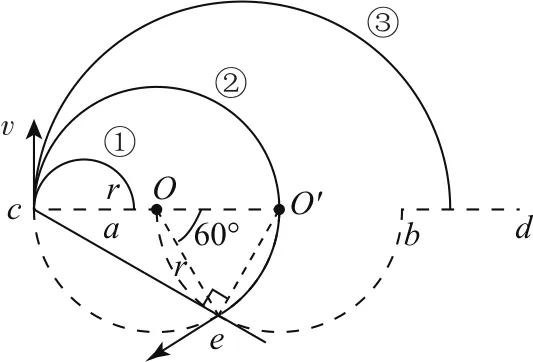
圖2

設半圓磁場半徑為R,則當半徑r≤0.5R和r≥1.5R時,粒子分別從ac、bd區域射出,磁場中的軌跡為半圓,運動時間等于半個周期(圖2中軌跡①③).

當0.5R＜r＜1.5R時,粒子從半圓邊界射出.將軌跡半徑從0.5R逐漸放大,粒子射出位置從半圓頂端向下移動,軌跡圓心角從π逐漸增大,當軌跡半徑為R時,軌跡圓心角最大(圖2中軌跡②ce恰與eO′垂直).然后再增大軌跡半徑,軌跡圓心角減小,因此當軌跡半徑等于R時軌跡圓心角最大,即軌跡對應的最大圓心角粒子運動最長時間為故選C.

點評

這道題難度適中,重視對基本概念、基本規律的考查.主要考查了洛倫茲力、圓周運動規律等基本知識和基本方法,引導學生重視基礎、回歸教材,體現了從知識能力目標向“核心價值、學科素養、關鍵能力、必備知識”四位一體綜合考查的轉變,對物理教學具有很好的導向作用.要特別注意的是,如果粒子周期相同,那么無論軌跡圓大小,運動時間的大小都取決于偏向角.

高考結束后,筆者通過與學生交流,得知造成一部分學生失分的原因是本題屬于“圓弧＋單直線邊界類”的非常規問題,而學生只熟悉常規邊界問題,他們在平時練習時忽視挖掘解題規律方法,單純機械地“刷題”,導致解題水平不能逐步提高.為了使教學更加有效,筆者整理了近幾年試題中常見的非常規邊界磁場問題,總結了相應的解題策略,以供參考.

1 非常規邊界磁場

1.1 不平行兩射線邊界

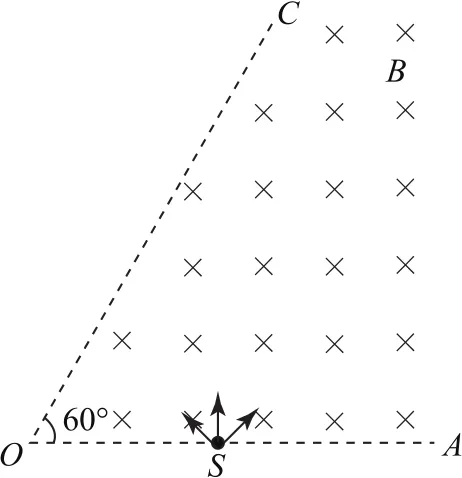
圖3

例2如圖3所示,邊界OA與OC之間分布有垂直紙面向里的勻強磁場,邊界OA上有一粒子源S.某一時刻,從S平行于紙面向各個方向發射出大量帶正電的同種粒子(不計粒子的重力及粒子間的相互作用),所有粒子的初速度大小相同,經過一段時間有大量粒子從邊界OC射出磁場.已知∠AOC＝60°,從邊界OC射出的粒子在磁場中運動的最長時間等于為粒子在磁場中運動的周期),則從邊界OC射出的粒子在磁場中運動的時間可能為( ).

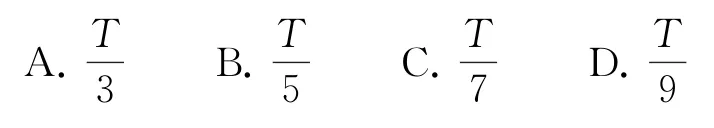
解析

粒子在磁場中做勻速圓周運動,出射點和入射點的連線即為軌跡的弦,初速度大小相同,軌跡半徑R相同,可用動態定圓法.

圖4中,設OS＝d,當出射點D與S點的連線垂直于OA時,DS弦為直徑是最長弦,軌跡所對的圓心角最大,周期一定,則粒子在磁場中運動的時間最長.由此得到,軌跡半徑當出射點E與S點的連線垂直于OC時,弦ES最短,軌跡所對的圓心角最小,則粒子在磁場中運動的時間最短.則,由幾何知識得θ＝60°,最短時間.

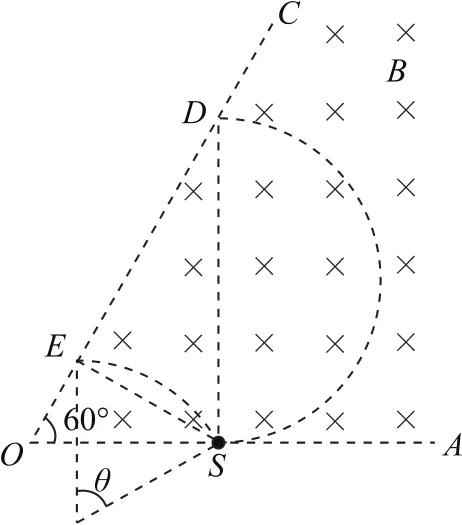
圖4

點評

面對此類問題時,要認真審題,提取條件,考慮比較軌跡半徑大小,究竟是使用“動態定圓法”還是“放縮圓法”;還要選擇時間的表達式,本題用弦長的變化來觀察、比較時間的變化,更加直觀,臨界條件是DS弦為直徑并且是最長弦,更易得出.

1.2 扇形邊界

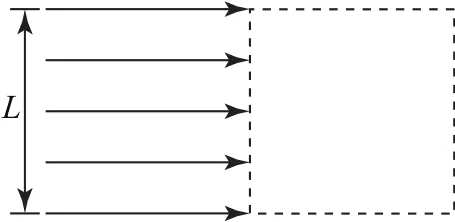
圖5

例3如圖5所示,紙面內有寬為L,水平向右飛行的帶電粒子流,粒子質量為m、電荷量為－q、速率為v0,不考慮粒子的重力及相互間的作用,要使粒子都匯聚到一點,可以在粒子流的右側虛線框內設計一勻強磁場區域,則磁場區域的形狀及對應的磁感應強度可以是哪一種(其中選項中曲線均為半徑是L的圓弧,B選項中曲線為半徑是的圓)( ).

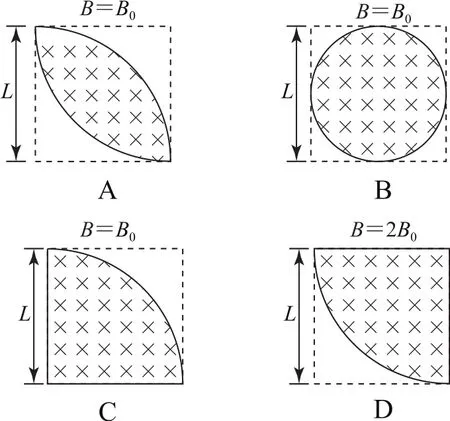
解析

本題中,軌跡圓半徑等于磁場圓半徑,根據磁匯聚結論:平行射入圓形有界磁場的相同帶電粒子,如果圓形磁場的半徑與圓軌跡半徑相等,則所有粒子都從磁場邊界上的同一點射出,并且出射點的切線與入射速度方向平行,可知選項A正確.

1.3 多邊形邊界

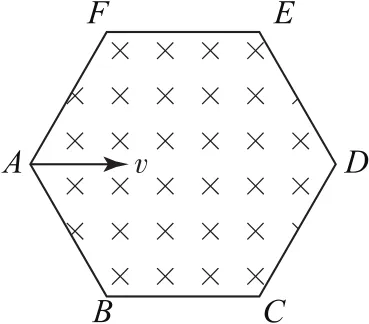
圖6

例4如圖6所示,在一個邊長為a的正六邊形區域內存在磁感應強度為B,方向垂直于紙面向里的勻強磁場.3個相同的帶正電粒子,比荷先后從A點沿AD方向以大小不等的速度射入勻強磁場區域,粒子在運動過程中只受磁場力作用.已知編號為①的粒子恰好從F點飛出磁場區域,編號為②的粒子恰好從E點飛出磁場區域,編號為③的粒子從ED邊上某一點垂直邊界飛出磁場區域.則( ).

C.三個粒子進入磁場的速度依次減小

D.三個粒子在磁場內運動的時間依次增加

圖7

解析

由圖7可知,粒子運動半徑逐漸增大,故速度增大.結合可知三個粒子在磁場內運動的時間依次減小故選項B正確.

1.4 組合邊界

例5如圖8所示,半徑為R的圓形區域內有垂直于圓平面向里的勻強磁場,磁感應強度大小為B,O為圓心,∠AOC＝90°,D為AC的中點,DO為一塊很薄的粒子吸收板,一束質量為m、電荷量為e的電子以相同速度在AD間平行于DO方向垂直射入磁場,不考慮電子的重力及相互作用,電子打在吸收板上即被板吸收,則電子在磁場中運動的時間可能為( ).

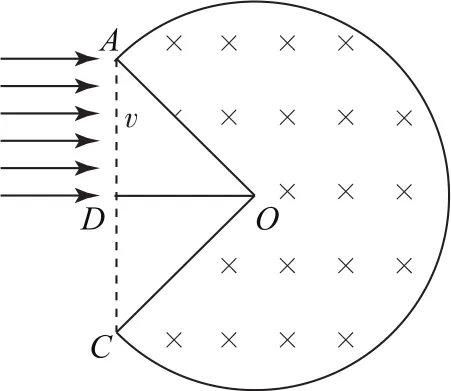
圖8

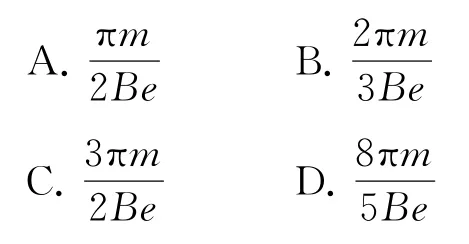
解析

本題重在利用動態定圓法進行觀察分析.由電子在磁場中做圓周運動的周期畫出電子在磁場中運動的軌跡如圖9所示.可知從AO邊射出磁場的電子在磁場中運動圓周,其運動時間為從CO邊射出磁場的電子在磁場中運動等于或大于圓周,其運動時間為其中沿DO方向從O點射入磁場的電子在磁場中運動圓周,恰好軌跡與磁場圓相切,其運動時間最長,最長時間故選項A、C正確.

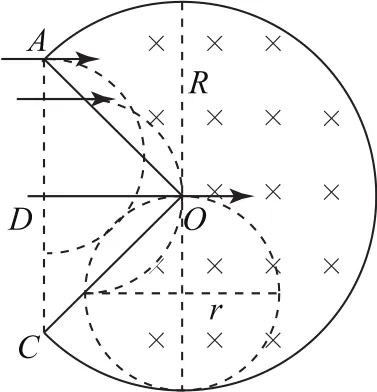
圖9

點評

此類組合邊界可能有扇形＋扇形、直角＋扇形、多個扇形＋無磁場扇形等.例如2016年浙江卷第25題“扇形聚焦回旋加速器”,就是多個扇形＋無磁場扇形類型(圖10).

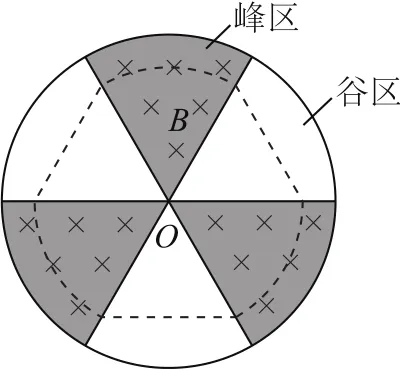
圖10

1.5 未知邊界

例6如圖11所示,質量為m＝8.0×10－25kg、電荷量為q＝1.6×10－15C的帶正電粒子從坐標原點O處沿xOy平面射入第一象限內,且與x方向夾角大于等于30°的范圍內,粒子射入時的速度方向不同,但大小均為v＝2.0×107m·s－1.現在某一區域內加一方向向里且垂直于xOy平面的勻強磁場,磁感應強度大小為B＝0.1T,若這些粒子穿過磁場后都能射到與y軸平行的熒光屏MN上,并且當把熒光屏MN向左移動時,屏上光斑長度和位置保持不變.畫出所加磁場的最小范圍(用斜線表示).

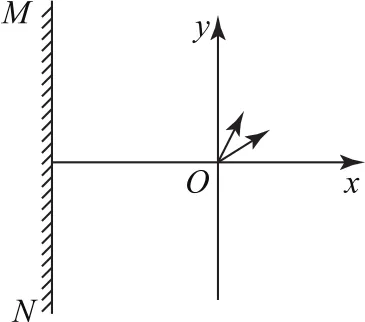
圖11

解析

由題意得,軌跡半徑R＝0.1m.當把熒光屏MN向左移動時,屏上光斑長度和位置保持不變,說明電子出射方向平行,都沿x軸負方向,逆向使用磁發散的規律,所加磁場若為整個圓形,則半徑為R＝0.1m.問最小磁場范圍就是所有粒子運動的范圍即邊界OB和OC弧與磁場圓所夾范圍,如圖12陰影部分.

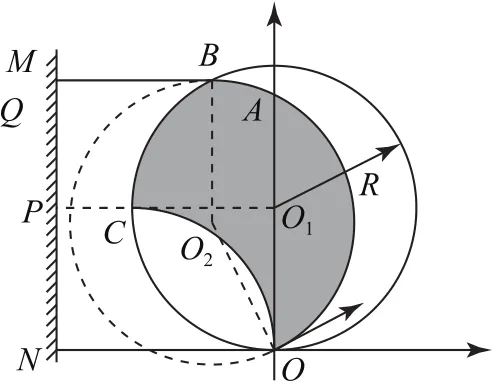
圖12

例7如圖13所示,虛線MO與水平線PQ相交于O,二者夾角θ＝30°,在MO左側存在電場強度為E、方向豎直向下的勻強電場,MO右側某個區域存在磁感應強度為B、垂直紙面向里的勻強磁場,O點處在磁場的邊界上.現有一群質量為m、電荷量為＋q的帶電粒子在紙面內以一定范圍的速度垂直于MO從O點射入磁場,所有粒子通過直線MO時,速度方向均平行于PQ向左.不計粒子的重力和粒子間的相互作用力,求磁場區域的最小面積.

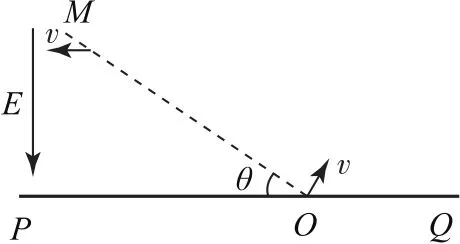
圖13

解析

由“速度大小不同的粒子均要水平通過MO”可知粒子飛出磁場的位置均應在ON的連線上(如圖14),故磁場范圍的最小面積S是速度最大的粒子在磁場中的軌跡與ON所圍成圖形的面積.

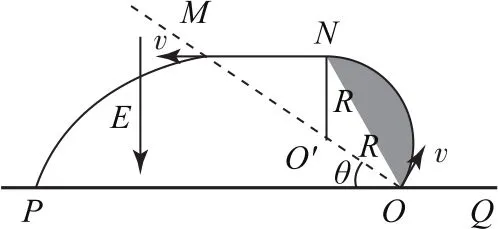
圖14

答案.

2 解題策略

策略1嚴格規范作圖步驟,定圓心—定半徑—定軌跡—定圓心角(回旋角).

那么,如何確定“圓心角與時間”呢?注意以下問題破解規律:

1)速度的偏向角φ既等于軌跡圓弧所對應的圓心角(回旋角)θ,又等于2倍的弦切角α(當偏向角為鈍角時為π＋2α),如圖15所示.

2)時間的計算方法.

a)由圓心角求.由知,如果粒子周期相同,那么無論軌跡圓大小,t的大小都取決于偏向角.另外,有.

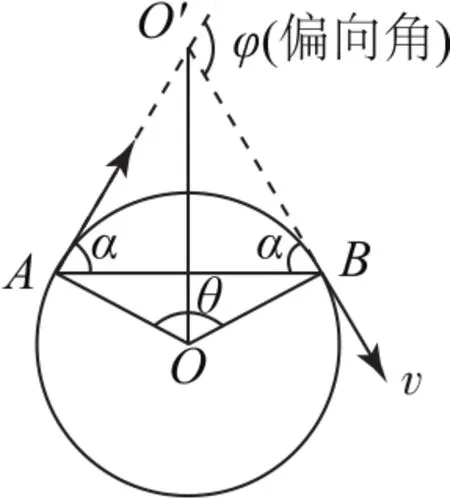
圖15

b)由弧長求.此方法多用于v相同時,弧長s便于觀察長短的情況.

c)同一軌跡,劣弧下,弦長越長,粒子運動時間越長,優弧則相反.

策略2觀察幾何圖形,找邊角關系,尤其要注意磁匯聚、磁發散二級結論條件是否滿足.

當圓形磁場的半徑與圓軌跡半徑相等時,存在兩條特殊規律:

1)(磁發散)如圖16-甲圖所示.

2)(磁匯聚)如圖16-乙圖所示.

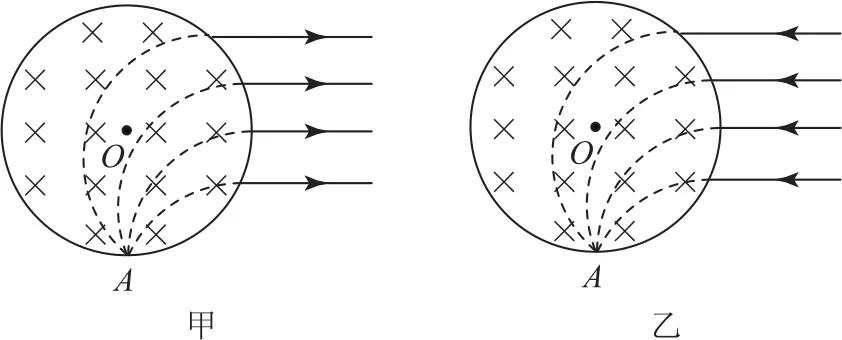
圖16

策略3從軌跡入手找準臨界條件.

1)當粒子的入射方向不變而速度大小可變時,由于半徑不確定,可從軌跡圓的縮放中發現臨界點.

2)當粒子的入射速度大小確定而方向不確定時,軌跡圓大小不變,只是位置關于入射點發生了旋轉,可從定圓的動態旋轉中發現臨界點.

策略4梯度性習題的訓練.

只有教師“跳入題海”,找出合適的梯度性習題,才能讓學生“題海上泛輕舟”.所以,教師一定要關注各級考試試題,把其中有代表性的試題歸類總結,整理成專題,注意專題的訓練難度應由易到難、由舊到新,這樣才能讓學生在有限時間內實現高效的學習.